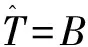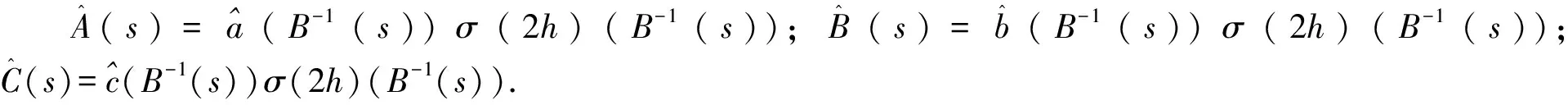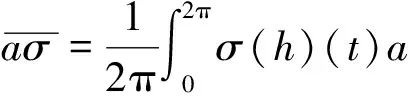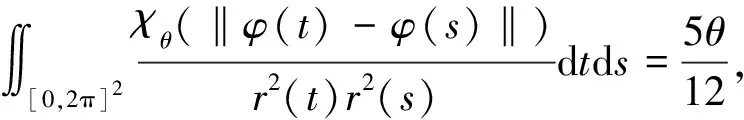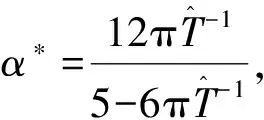阻尼奇異微分方程周期解的扭轉(zhuǎn)性
丁 錦 紅
(河海大學(xué) 理學(xué)院數(shù)學(xué)系, 南京 210098)
0 引 言
對(duì)時(shí)間周期非線性微分方程平衡點(diǎn)的Lyapunov穩(wěn)定性研究是微分方程與動(dòng)力系統(tǒng)的一個(gè)重要問(wèn)題. 然而, 研究保守系統(tǒng)的穩(wěn)定性很困難, 因?yàn)長(zhǎng)yapunov直接方法不適用. 文獻(xiàn)[1-8]在Birkhoff標(biāo)準(zhǔn)型和Moser扭轉(zhuǎn)定理的基礎(chǔ)上, 發(fā)展了研究二階拉格朗日方程穩(wěn)定性的解析方法, 即三階近似方法.
文獻(xiàn)[8-9]將上述方法推廣到帶有阻尼的二階微分方程中, 即計(jì)算了二階非線性微分方程
x″+h(t)x′+f(t,x)=0
(1)
的三階近似方程
x″+h(t)x′+a(t)x+b(t)x2+c(t)x3+…=0
(2)
的第一扭轉(zhuǎn)系數(shù)β, 其中:f: R×R→ R是關(guān)于t的2π-周期函數(shù), 且充分光滑;
若ψ(t)是方程(1)的2π-周期解, 則方程(2)中的系數(shù)a,b,c∈C(R/2πZ), 且
若β≠0, 則稱解ψ(t)是扭轉(zhuǎn)的. 由Moser扭轉(zhuǎn)定理可知, 此扭轉(zhuǎn)周期解在Lyapunov意義下是穩(wěn)定的.
方程(2)的一階線性部分是
x″+h(t)x′+a(t)x=0.
(3)
文獻(xiàn)[9]給出了關(guān)于式(3)的穩(wěn)定性準(zhǔn)則. 但式(3)的穩(wěn)定性并不能保證方程(1)的穩(wěn)定性.
本文考慮阻尼奇異微分方程
(4)
1 預(yù)備知識(shí)
引理1[8-9]方程(2)的扭轉(zhuǎn)系數(shù)為
其中:
θ=2πρ,ρ是Hill方程
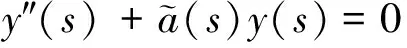
(6)
的旋轉(zhuǎn)數(shù);r是奇異方程
(7)
的唯一正2π-周期解, 且滿足
這里
引理2[10]假設(shè)
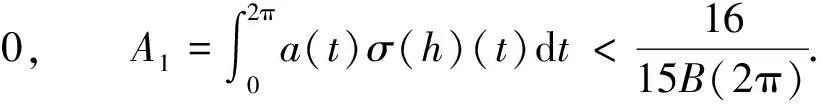
(8)
則存在0 1) 方程(7)唯一的正2π-周期解滿足 (9) 2) 方程(6)的旋轉(zhuǎn)度ρ滿足 (10) 由文獻(xiàn)[11]可知, 當(dāng)滿足條件(8)時(shí), 對(duì)于任意的α>0, 方程(4)有一個(gè)正的2π-周期解. 定理1存在常數(shù)L(α)>0, 使得如果a,h滿足條件: (11) 則存在一個(gè)正常數(shù)α*, 對(duì)于所有的α>0且α≠α*, 方程(4)的正周期解都是穩(wěn)定的. 證明: 設(shè)ψ(t)是奇異方程(4)的正2π-周期解, 則其三階近似可寫為 (12) 其中: (13) 將式(12)兩邊同乘σ(h)(t), 可得 (14) 將方程(4)兩邊同乘σ(h)(t), 有 (15) 再將方程(15)兩邊同時(shí)積分可得 (16) (17) 由文獻(xiàn)[10]可知, 0<γ(1-S(A1))≤ψ(t)≤γ(1+S(A1)), 且當(dāng)A1→ 0+時(shí),ψmax/ψmin=1+O(A1). 故當(dāng)式(11)成立時(shí), 若A1→ 0+, 則有 又由式(9)與(10)可知 故有 根據(jù)式(5),(13)和(17), 奇異方程(4)的扭轉(zhuǎn)系數(shù)β為 (23) 第二項(xiàng)為 (24) 又由式(23)和(24), 當(dāng)A1→ 0+時(shí), [1] LEI Jin-zhi, LI Xiong, YAN Ping, et al. Twist Character of the Least Amplitude Periodic Solution of the Forced Pendulum [J]. SIAM J Math Anal, 2003, 35(4): 844-867. [2] Ortega R. Periodic Solution of a Newtonian Equation: Stability by the Third Approximation [J]. J Differential Equations, 1996, 128(2): 491-518. [3] Ortega R. The Stability of the Equilibrium: A Search for the Right Approximation [M]. Ten Mathematical Essays on Approximation in Analysis and Topology. Amsterdam: Elsevier, 2005: 215-234. [4] Torres P J. Twist Solutions of a Hill’s Equations with Singular Term [J]. Adv Nonlinear Stud, 2002, 2(3): 279-287. [5] Torres P J. Existence and Stability of Periodic Solutions for Second Order Semilinear Differential Equations with a Singular Nonlinearity [J]. Proc Royal Soc Edinburgh: Ser A, 2007, 137(1): 195-201. [6] ZHANG Mei-rong. The Best Bound on the Rotations in the Stability of Periodic Solutions of a Newtonian Equation [J]. J London Math Soc, 2003, 67(1): 137-148. [7] CHU Ji-feng, LEI Jin-zhi, ZHANG Mei-rong. The Stability of the Equilibrium of a Nonlinear Planar System and Application to the Relativistic Oscillator [J]. J Differential Equations, 2009, 247(2): 530-542. [8] CHU Ji-feng, LEI Jin-zhi, ZHANG Mei-rong. Lyapunov Stability for Conservative Systems with Lower Degree of Freedom [J]. Discrete Contin Dyn Syst: Ser B, 2011, 16(2): 423-443. [9] CHU Ji-feng, XIA Ting. The Lyapunov Stability for the Linear and Nonlinear Damped Oscillator with Time-Periodic Parameters [J/OL]. Abstract and Applied Analysis, 2010, doi: 10.1155/2010/286040. [10] CHU Ji-feng, ZHANG Mei-rong. Rotation Numbers and Lyapunov Stability of Elliptic Periodic Solutions [J]. Discrete Contin Dyn Syst, 2008, 21(4): 1071-1094. [11] CHU Ji-feng, FAN Ning, Torres P J. Periodic Solutions for Second Order Singular Damped Differential Equations [J]. J Math Anal Appl, 2012, 388(2): 665-675.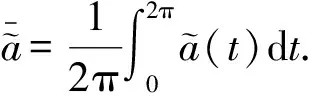
2 主要結(jié)果