劉 霞, 李曉焱,2, 李曉娜

(1.榆林學(xué)院數(shù)學(xué)系,陜西榆林719000;2.西安建筑科技大學(xué)數(shù)學(xué)系,陜西西安710055)

1 引言和預(yù)備知識

設(shè)C是實(shí)Hilbert空間H的非空閉凸子集,T:C→H是非擴(kuò)張映像,則對于?x,y∈C,‖Tx-Ty‖≤‖x-y‖.F(T)={x∈C:x=Tx}為T的不動點(diǎn)集.度量(最近點(diǎn))投影映射PC:H→C指:對?x∈H,PCx是C中的唯一的點(diǎn),且‖x-PCx‖=inf{‖x-y‖:y∈C}.如果 F(T)≠φ,可以證明 F(T)是 Hilbert空間中非空閉凸子集,于是存在唯一的x?∈F(T)滿足‖x?‖=min{‖x‖:x∈F(T)},則稱 x?是T的最小范數(shù)不動點(diǎn),從而 x?是從原點(diǎn)到F(T)的最近點(diǎn)投影,即x?=PF(T)(0).記:xn→x表示{xn}強(qiáng)收斂于 x;xn?x表示{xn}弱收斂于 x;w={x:?xnj?x}為{xn}的弱極限集.

文獻(xiàn)[1]對Halpern[2]方法做了改進(jìn),當(dāng)0?C,修改后的迭代序列xn依然收斂于C中一個不動點(diǎn).在此基礎(chǔ)上,結(jié)合文獻(xiàn)[3-10],利用平行算法和最近點(diǎn)投影算子對有限多非擴(kuò)張映像的最小范數(shù)不動點(diǎn)做進(jìn)一步地研究.

性質(zhì)1[1,6,11]投影映射的基本性質(zhì)

(i)＜x-PCx,y-PCx＞≤0,?x∈H,?y∈C;

(ii)＜x-y,PCx-PCy＞≥‖PCx-PCy‖2,?x,y∈H;

(iii)‖x-PCx‖2≤‖x-y‖2-‖y-PCx‖2,?x∈H,?y∈C.

引理1[1,5]半閉原理,設(shè)C是實(shí)Hilbert空間H的非空閉凸子集,T:C→C是非擴(kuò)張映射,當(dāng) n→∞時,如果 xn?p,且‖xn-Txn‖→0,則 p是T的不動點(diǎn),即 p∈F(T).引理2[1,6,12]設(shè){αn}是一個滿足下列條件的非負(fù)實(shí)數(shù)序列

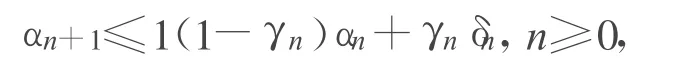
2 主要結(jié)果

引理3 設(shè)C是實(shí)Hilbert空間H的非空閉凸子集,{T1,…,Tn}是C上的N個非擴(kuò)張自映射,對于所有的1≤i≤N,λi＞0,且,那么算子是非擴(kuò)張的 .

證明 對任意的 x,y∈C,有

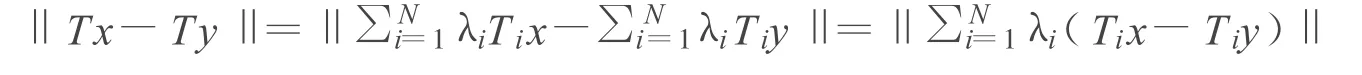
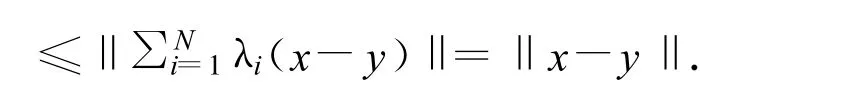
定理 設(shè) C是實(shí)Hilbert空間 H的非空閉凸子集,{T1,…,TN}是 C上的N個非擴(kuò)張自映射,且φ≠F(T):=∩Ni=1F(Ti)=(T1T2…tN),假定{tn}滿足下列條件:

(B1)

任取初始值x0∈C,序列{xn}通過平行算法定義為則序列{xn}強(qiáng)收斂于非擴(kuò)張映像的公共最小范數(shù)不動點(diǎn).

證明 (1)證明{xn}有界.任取 p∈F(T)由式(1)可推得

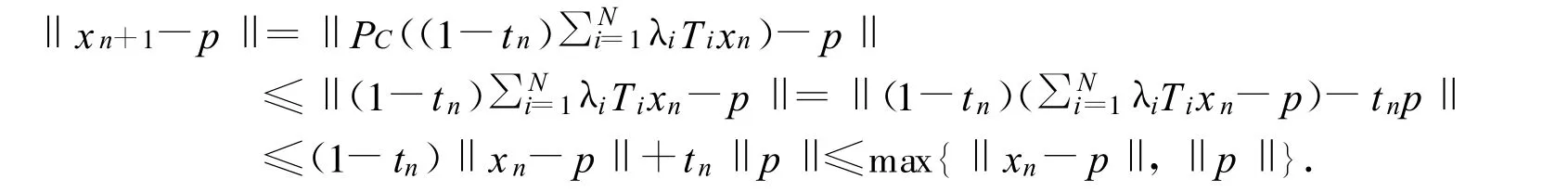
所以,對所有的 n≥0歸納可得:‖xn-p‖≤max{‖x0-p‖,‖p‖}.于是序列{xn}有界,即存在 M＞0,使對所有的 n,恒有 M≥max{‖xn‖,‖Txn‖}成立.

(2)證明‖xn+1-xn‖→0.利用 PC的非擴(kuò)張性和式(1)得

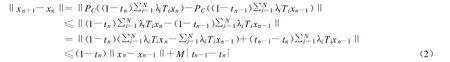
由引理2,條件(B3)和式(2)可得‖xn+1-xn‖→0.

(3)證明 ωn(xn)?F(T).

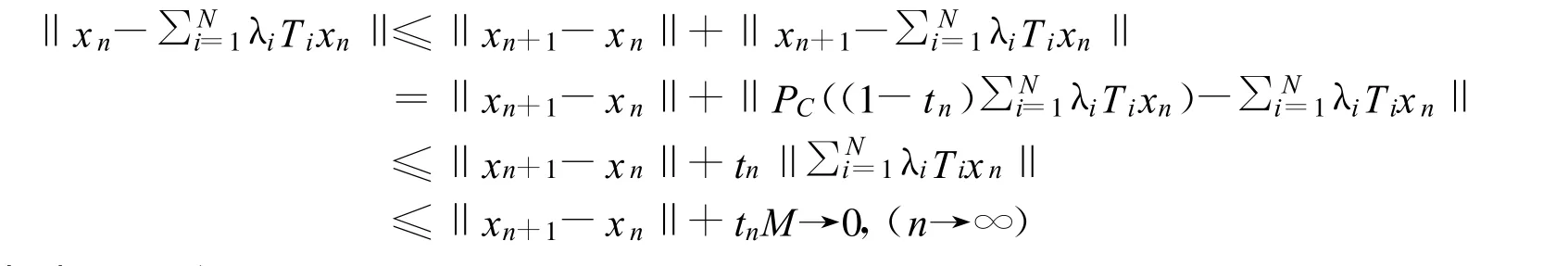
由引理1可得 ωn(xn)?F(T).

因?yàn)閧xn}有界,所以不失一般性可設(shè) xn′?x′∈F(T).又 x?=PF(T)(0),所以由性質(zhì) 1(i)和(3)式可得

(5)最后證明xn→x?

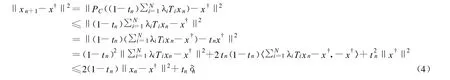
其中

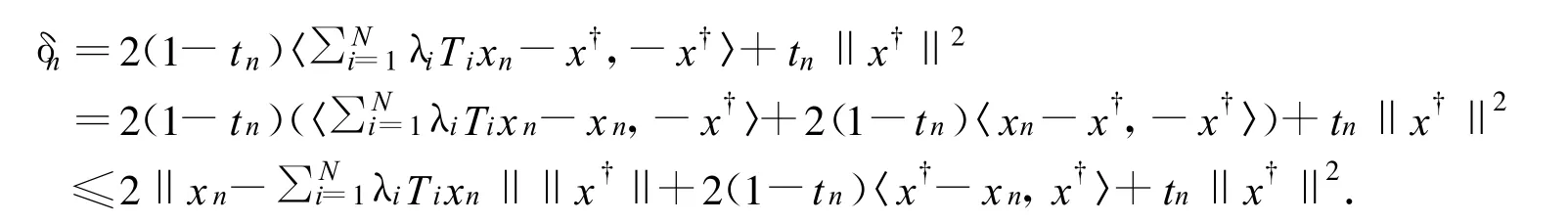
如果上述定理只有一個映射,即i=1,則有下述推論成立.

推論 設(shè)C是Hilbert空間H的非空閉凸子集,T:C→C非擴(kuò)張映像,F(T)≠φ,x0∈C.設(shè){tn}∈(0,1),并滿足上述定理中的(B1),(B2),(B3)條件.序列{xn}定義為

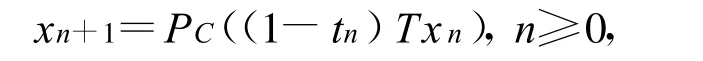
則

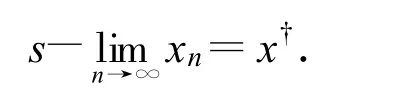
致謝:感謝榆林學(xué)院科研啟動項(xiàng)目(11gk64)對本文的資助

[1] Y L Cuiand,X Liu.Noteson Browder's and Halpern's methods for nonexpansive mappings[J].Fixed Point Theory,2009,10(1):89-98.

[2] B Halpern.Fixed points of nonexpanding maps[J].Bull.Amer.Math.Soc.,1967,73:957-961.

[3] S Reich.Approximating fixed points of nonexpansive mappings[J].Panamerican.Math.J.1994,4(2):23-28.

[4] H K Xu.Iterative algorithms for nonlinear operators[J].J.London Math.Soc.,2002,66:240-256.

[5] H K Xu.Remarks on an iterative method for nonexpansive mappings[J].Comm.Appl.Nonlinear Anal.2003,10(1):67-75.

[6] Y H Yao,R D Chen,H K Xu.Schemes for finding minimum-norm solutions of variational inequalities[J].Nonlinear Analysis,2010,72:3447-3456.

[7] F E Browder.Convergence theorems for sequences of nonlinear operators in Banach spaces[J].Math.Z.,1967,100:201-225.

[8] Z Opial.Weak convergence of the sequence of successive approximations of nonexpansive Bull.Amer.Math.Soc.mappings,1967,73:595-597.

[9] R.Wittmann,Approximation of fixed points of nonexpansive mappings[J].Arch.Math.1992,58:486-491.

[10] D P Wu.Weak Convergence of Ishikawa Iteration with Error for Pseudo Contractive Mappings in Hilbert Spaces[J].Journal of Mathematics Research,2011,3(4):44-49.

[11] K Geobeland,W A Kirk.Topicsin Metric Fixed Point Theory[M].Cambridge Studiesin Advanced Mathematics.Cambridge University Press,1990.

[12] H K Xu.Strong convergence of an iterative method for nonexpansive and accretive operators[J].J.Math.Anal.Appl.2006,314:631-643.