唐元義 許厚澤 胡清峰 駱有隆

(湖北大學(xué)數(shù)學(xué)與計(jì)算機(jī)科學(xué)學(xué)院1) 武漢 430062)

(中國(guó)科學(xué)院測(cè)量與地球物理研究動(dòng)力大地測(cè)量學(xué)重點(diǎn)實(shí)驗(yàn)室2) 武漢 430077)

(武漢理工大學(xué)管理學(xué)院3) 武漢 430070)

0 引 言

大地測(cè)量邊值問題,一般利用Stokes公式,采用有限差分法或快速富氏變換(FFT)等來計(jì)算.唐元義等研究了用自然邊界元法對(duì)大地測(cè)量的第二、第三邊值問題進(jìn)行求解[1-2],所采用的方法是由Neumann外問題得大地測(cè)量邊值問題的自然積分方程,然后再離散求解.

現(xiàn)在根據(jù)自然邊界元的基本思想,直接得到大地測(cè)量Stokes邊值問題的自然積分方程,再用離散化技術(shù)進(jìn)行求解.

1 Stokes邊值問題

地球重力場(chǎng)可以用地球重力位來表達(dá).通常把重力位W分成2部分:正常重力位U和擾動(dòng)位T.正常重力位U可用4個(gè)大地測(cè)量基本參數(shù)來確定,是一個(gè)已知函數(shù);擾動(dòng)位 T是一個(gè)待求的微量函數(shù).大地測(cè)量邊值問題,就是利用觀測(cè)數(shù)據(jù)給定邊值條件,來推求擾動(dòng)位及外部重力場(chǎng)的問題.

假定通過重力歸算,已經(jīng)把大地水準(zhǔn)面外的地球質(zhì)量去掉,并假定正常橢球中心與地球質(zhì)心重合,旋轉(zhuǎn)角速度等于地球自轉(zhuǎn)角速度,則大地水準(zhǔn)面外空間的擾動(dòng)位滿足Lap lace微分方程,即Δt=0,而且在無窮遠(yuǎn)處是正則的.

已知觀測(cè)量是重力異常 Δg,求擾動(dòng)位的問題,就是大地測(cè)量Stokes邊值問題

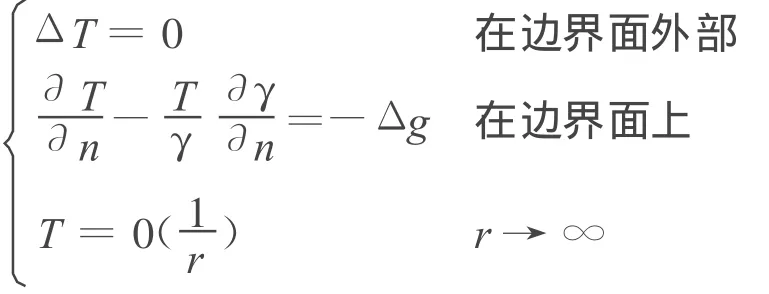
上面第一式為擾動(dòng)位 T的Lap lace方程;第二式為物理大地測(cè)量學(xué)的基本微分關(guān)系.式中γ為正常重力,左端是T和 的線性組合(n為邊界面的外法線方向),右端的重力異常是已知的,邊界面一般為大地水準(zhǔn)面.

用球面近似代替大地水準(zhǔn)面,即所謂的球近似,這使 T具有扁率級(jí)的誤差.物理大地測(cè)量Stokes邊值問題,在球近似的情形下可歸結(jié)為如下的Robin問題

式中:S為球面,SC球面外部.

2 擾動(dòng)位的Poisson積分式表示

由于擾動(dòng)位 T=W-U是諧函數(shù),可以用Poisson積分式表示為

式中 :T(r,θ,λ)為計(jì)算點(diǎn)的擾動(dòng)位 ;T(R,θ′,λ′)為球面r=R上的擾動(dòng)位;ψ為球面上計(jì)算點(diǎn)(θ,λ)與積分流動(dòng)點(diǎn)(θ′,λ′)的球心角

擾動(dòng)位 T(r,θ,λ)也寫成諧函數(shù)級(jí)數(shù)形式

式中:Tl(θ,λ)為 l階的 Lap lace面諧函數(shù)

將式(1)對(duì)r求導(dǎo),得諧函數(shù)的徑向?qū)?shù)

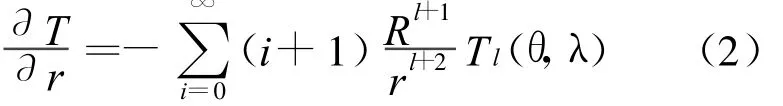
在地球外,邊值條件為

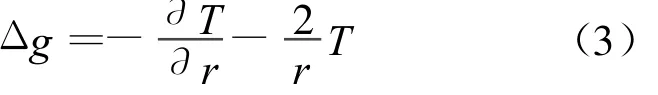
將式(2)代入式(3)得

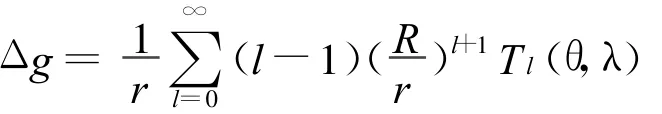
當(dāng)r=R時(shí),就變?yōu)?/p>

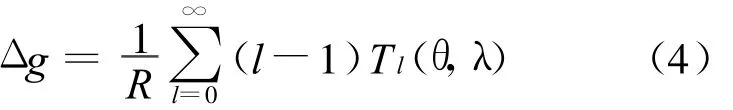
即為重力異常的球諧表達(dá)式.

3 邊值問題的自然邊界元法

在式(4)兩邊同時(shí)乘以γˉT,?γˉT∈T(S)(γ為跡算子,T(S)由自然積分算子K導(dǎo)出的跡空間[3]),再作內(nèi)積,也仍相等,即有

式中:(· ,·)為內(nèi)積(球面積分)如下式

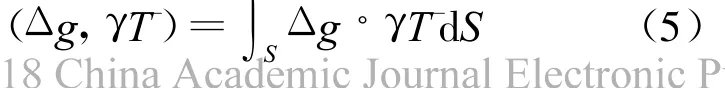
則有

從式(7)可以看出,用離散化技術(shù)求解對(duì)自然積分方程,就可求出球面S(大地水準(zhǔn)面)上的擾動(dòng)位 T了(擾動(dòng)位 T含在Tl(θ,λ)中).

4 邊值問題的自然邊界元求解

對(duì)球面S作有限元剖分,Sh(S)為相應(yīng)于該剖分、由適當(dāng)選取的基函數(shù)張成的H1/2(S)的線性子空間,得到自然積分方程的近似變分問題[4].

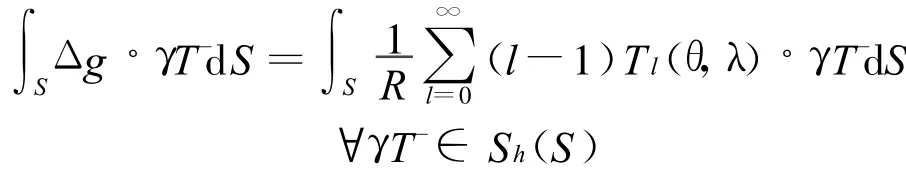
設(shè)

由此構(gòu)造球面S上的分片雙線性插值基函數(shù)Φ0(θ,φ)=L0(θ),Φ1(θ,φ)=LN1(θ),Φsj(θ,φ)=Ls(θ)Mj(φ),s=1,2,…,N1-1;j=1,2,…,N2.則 Sh(S)=span{Φ0(θ,φ),Φ1(θ,φ),Φsj(θ,φ),s=1,2,…,N1-1,j=1,2,…,N2}?H1(S)

設(shè) Th0(θ,φ)=T0Φ0(θ,φ)+T1Φ1(θ,φ)取S上的基函數(shù),則由自然積分方程可得線性方程組

5 結(jié) 束 語(yǔ)

大地測(cè)量Stokes公式是傳統(tǒng)的經(jīng)典公式,利用有限差分法或FFT,早為大地測(cè)量學(xué)家們所公認(rèn)和采用.而大地測(cè)量邊值問題的自然邊界元法,用的是邊界元法,在理論上是完全正確的.

當(dāng)然,在實(shí)際應(yīng)用中,即在作數(shù)值計(jì)算的時(shí),實(shí)際效果如何,是否具有比傳統(tǒng)的有限差分法更具有優(yōu)勢(shì),或與有限差分法結(jié)合起來,或者與有限元法結(jié)合,取長(zhǎng)補(bǔ)短,等等許多問題,將是需要進(jìn)一步深入研究的課題.

[1]唐元義.GPS-邊值問題的自然邊界元解法[J].武漢理工大學(xué)學(xué)報(bào):交通科學(xué)與工程版,2007,31(2):266-269.

[2]唐元義,許厚澤.物理大地測(cè)量邊值問題的自然邊界元解法[J].武漢理工大學(xué)學(xué)報(bào):交通科學(xué)與工程版,2008,32(1):146-148.

[3]余德浩.自然邊界元方法的數(shù)學(xué)理論[M].北京:科學(xué)出版社,1993.

[4]鄔吉明,余德浩.三維調(diào)和問題的自然積分方程及其數(shù)值解[J].計(jì)算數(shù)學(xué),1998,20(4):419-430.