趙煉恒 羅 強(qiáng) 楊 峰 李 亮 但漢成

(中南大學(xué)土木建筑學(xué)院1) 長沙 410075) (貴州省交通運輸廳基建處2) 貴陽 550003)

地基基礎(chǔ)承載力分析是巖土工程中的經(jīng)典問題[1-2].淺基礎(chǔ)臨近邊坡,直接將淺基礎(chǔ)置于邊坡上,或既有建筑物淺基礎(chǔ)一側(cè)進(jìn)行基坑開挖施工時,與水平地基不同,斜坡的存在必然對地基承載力有削減,其破壞模式也將有所不同[3-6].同時已有研究表明邊坡存在將導(dǎo)致地基承載力減損,但折減的程度及規(guī)律尚需要研究和探討.

本文根據(jù)線性破壞準(zhǔn)則和相關(guān)聯(lián)流動法則,利用極限分析中的機(jī)動法,構(gòu)建了一個邊坡基礎(chǔ)極限承載力的二維機(jī)動許可破壞模式.根據(jù)能耗相等原理獲得極限承載力的約束表達(dá)式,并把其轉(zhuǎn)化成了一個求含有非線性約束的最小值問題計算模型.通過編寫程序,對計算模型采用序列二次規(guī)劃法(SQP法)[7]進(jìn)行了優(yōu)化求解.研究結(jié)果與已有資料進(jìn)行了對比,并對影響斜坡地基承載力的部分參數(shù)進(jìn)行了敏感性分析.

1 剛性塊平動破壞機(jī)制

1.1 破壞機(jī)制

條形基礎(chǔ)寬B,邊坡傾斜角度 δ,邊坡上承受均布外荷q,假設(shè)基礎(chǔ)與地基不出現(xiàn)相對滑動,并假設(shè)臨坡條形淺基礎(chǔ)在極限承載力P u作用下,地基土出現(xiàn)單側(cè)平動破壞,破壞機(jī)制由(n+1)個三角形剛性塊組成,未知參數(shù) θ1,θ2,αi,βi 決定三角形剛體形狀,進(jìn)而決定破壞機(jī)制和速度場.如圖1,圖2所示.

根據(jù)圖1,由三角形簡單的幾何關(guān)系可計算各三角形邊長LAC,B1,D i,Li及面積Si(i=1,…,n).

根據(jù)圖2,由相容速度閉合的三角形幾何關(guān)系可計算各速度間斷線D i和L i上的速度Vi和Vi-1,i(i=1,…,n).

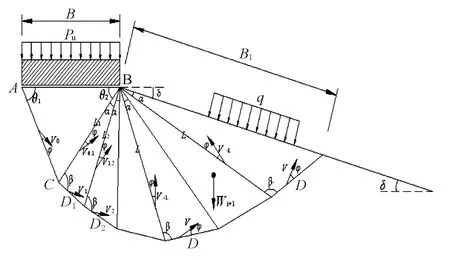
圖1 臨坡條基平動破壞機(jī)制及受力分析

1.2 能耗計算

能耗計算包括外力做功和內(nèi)部耗能兩方面.

圖2 相容速度三角形

由圖1～2可知,在極限承載力的作用下,外力的功率為:極限承載力Pu的功率WPu,條基下方三角形土重力的功率WABC,條基臨坡一側(cè)n個三角形剛塊土體重力的功率W soil,邊坡表面均布荷載q所做功率Wq.

條基為剛性基礎(chǔ),基礎(chǔ)下土體為理想剛體,無塑性變形,單側(cè)破壞模式的內(nèi)部耗能發(fā)生在速度間斷線上,包括Di,Li(i=1,…,n)上的內(nèi)部耗能∑Gi和∑Qi.另外,剛體ABC與一側(cè)土體的速度間斷線AC上亦有能量耗損GAC.

利用虛功率原理,根據(jù)破壞模式中外力所做功率與內(nèi)部耗能相等,將各能量計算式代入式(2)建立起極限承載力P u的計算表達(dá)式(3)有

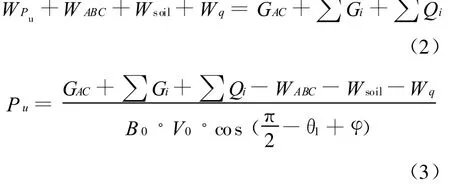
在式(2)中,B,γ,q,φ,c都是已知量,極限承載力P u 僅與未知參數(shù) θ1,θ2,αi,βi(i=1,…,n)有關(guān) .即所有的三角形單元幾何參數(shù),對于本文中含有k(k=n+1)個三角形剛體的單側(cè)破壞機(jī)構(gòu)而言共有2k個變量.很顯然,這些自變量應(yīng)滿足平動機(jī)制三角形剛體運動協(xié)調(diào)的速度場約束條件和物理意義要求的幾何約束條件.

工程中,Terzaghi地基承載力分項表達(dá)式被普遍使用.

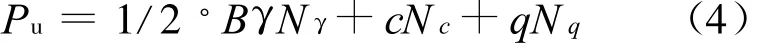
式中:Nc,Nq和Nγ分別代表臨近基坑土體黏聚力c,超載q和土體自重γ的影響系數(shù).

2 SQP優(yōu)化方法與實現(xiàn)

由以上分析可知,對于不同的自變量甚至是自變量組合,利用式(3)能得到不同的極限承載力上限解.但極限分析上限解總是大于真實極限荷載的,所以在上限解中越小的值則越接近真正的極限荷載值,則對以上上限分析的求解實際上轉(zhuǎn)化成了一個獲求含非線性約束的最小值問題.序列二次規(guī)劃算法(簡稱SQP法)適用于非線性較嚴(yán)重的問題.已有研究表明[8],對這類包含自變量θ1,θ2,αi,βi(i=1,…,n)約束條件和目標(biāo)函數(shù)極值Pu的非線性函數(shù),SQP法能夠獲得頗好的效果.

利用MATLAB軟件平臺,采用SQP法對該問題上限解進(jìn)行了優(yōu)化,15個剛性塊極限承載力平動破壞模式SQP優(yōu)化結(jié)果如圖3所示.其中,邊坡角 δ分別等于10,20,30°;巖土內(nèi)摩擦 φ=30°.其他參數(shù)滿足:c/(γB)=0.5;q/(γB)=0.25.

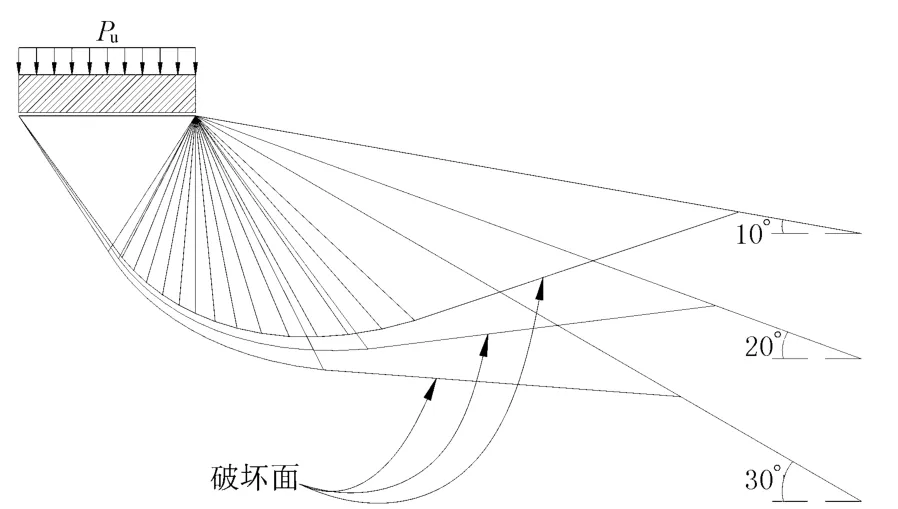
圖3 破壞機(jī)構(gòu)優(yōu)化結(jié)果

由圖3可看出:在其他參數(shù)一定的情況下,邊坡傾斜角度的增加將使地基破壞區(qū)域發(fā)生顯著變化,因而邊坡角度變化對條形基礎(chǔ)臨坡地基極限承載力的影響會很大.

3 數(shù)值計算對比與影響參數(shù)分析

3.1 計算精度控制

研究表明[8],極限上限分析中,剛性塊體劃分個數(shù)對結(jié)果的精確性和優(yōu)化效率的影響均較大.當(dāng)B=2m,φ=25°,δ=150,c=20 kPa,q=10 kPa,γ=20 kN/m3,劃分為不同剛性塊體數(shù)量時,對極限承載力值P u的最優(yōu)結(jié)果的影響如圖4所示.

由圖4知:隨著剛性塊的增多,P u將逐步減小并趨向于精確的解,且這種減小趨勢的變化率是迅速減小的.對于相同的計算參數(shù),當(dāng)剛性塊數(shù)量超過50個,剛性塊增多所得的P u量值變化很小.

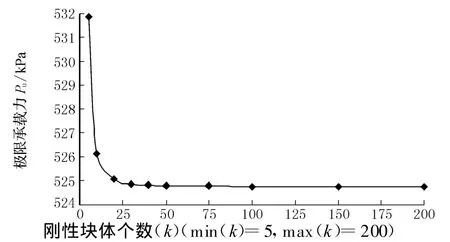
圖4 P u隨剛性塊個數(shù)變化情況

3.2 對比計算

本文計算結(jié)果與文獻(xiàn)[1-2]給出的極限承載力分項系數(shù)Nγ值的最小計算值結(jié)果進(jìn)行對比如表1.其中:Siva采用滑移線法;M eyerho f和M izuno采用極限平衡法;Chen,Saran采用了極限分析上限法.

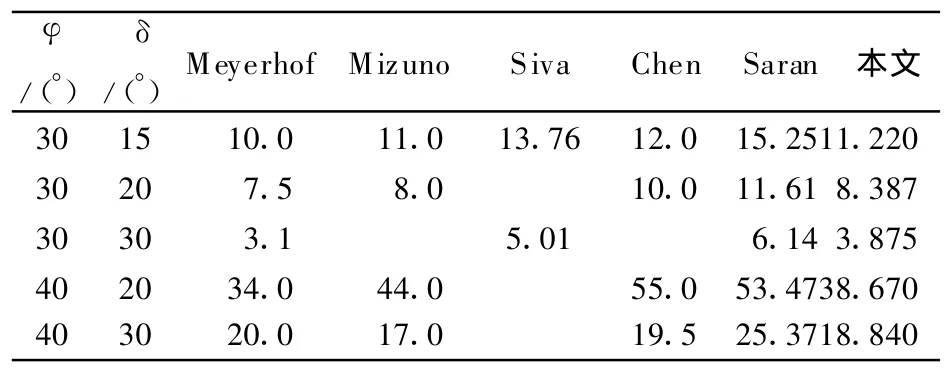
表1 N r計算與已有結(jié)果對比

由表1中的結(jié)果對比看出:采用極限分析上限法本文所得 Nγ值較Chen,Saran的結(jié)果小,是較好的上限解;與Siva的滑移線法以及Meyerhof和Mizuno的極限平衡法所得的 Nγ值也比較接近.進(jìn)而可以證明本文方法和編寫程序的正確性.

3.3 影響參數(shù)分析

承載力分項系數(shù) Nc,Nq已有公認(rèn)的解析表達(dá)式,而Nγ尚未獲得真實解.限于篇幅,以下主要分析內(nèi)摩擦角φ和邊坡傾角δ對Nγ,Nc,Nq的影響.

3.3.1 內(nèi)摩擦角對承載力分項系數(shù)影響 固定邊坡傾角δ而巖土體內(nèi)摩擦角φ變化,假設(shè)條基寬B=2 m且速度相容機(jī)構(gòu)劃分為50個剛性塊體時,分別Nγ,Nc,Nq系數(shù)值進(jìn)行優(yōu)化求解如圖5所示.δ和φ同時變化對各系數(shù)的影響如圖6所示.

由圖5看出:坡角δ不變的情況下,巖土體內(nèi)摩擦角φ數(shù)值增加對極限承載力分項系數(shù)Nγ,Nc,Nq的量值影響具有較強(qiáng)的非線性增加趨勢.

結(jié)合圖3,由圖5和圖6可知:巖土體內(nèi)摩擦角φ提高使各分項系數(shù)迅速增大,因而地基極限承載力顯著提高,而邊坡的存在對臨坡地基承載力存在較大的不利影響,且破壞區(qū)域亦將發(fā)生顯著變化.

3.3.2 邊坡傾角對承載力分項系數(shù)影響 固定巖土體內(nèi)摩擦角φ而邊坡傾角δ變化,假設(shè)條基寬B=2m且速度相容機(jī)構(gòu)劃分為50個剛性塊體時,分別Nγ,Nc,Nq系數(shù)值進(jìn)行優(yōu)化求解如圖7所示.δ和φ同時變化對各系數(shù)的影響如圖8所示.

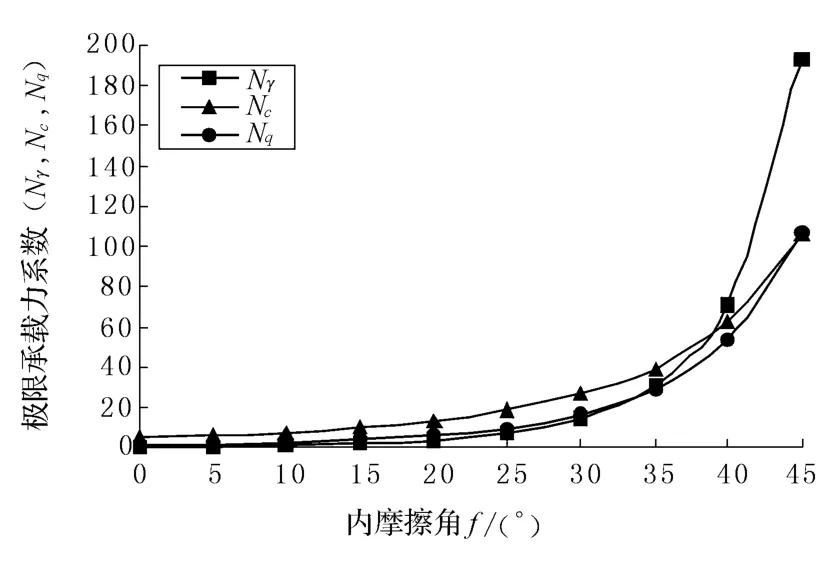
圖5 Nγ,Nc,Nq隨φ變化情況

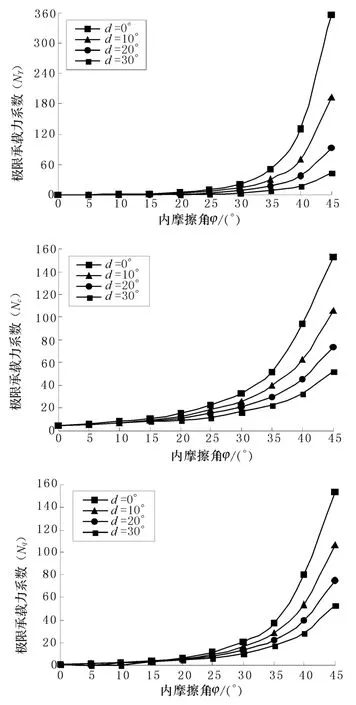
圖6 Nγ,Nc,Nq隨φ變化情況

由圖7可見,在巖土體內(nèi)摩擦角 φ一定的情況下,邊坡坡角增加對極限承載力分項系數(shù)的量值影響具有較強(qiáng)的非線性減小趨勢.

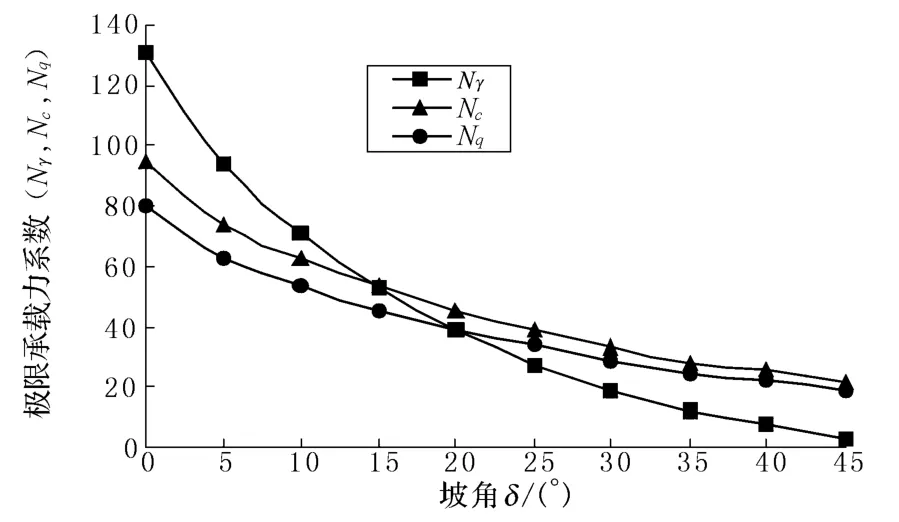
圖 7 Nγ,Nc,Nq隨δ變化情況

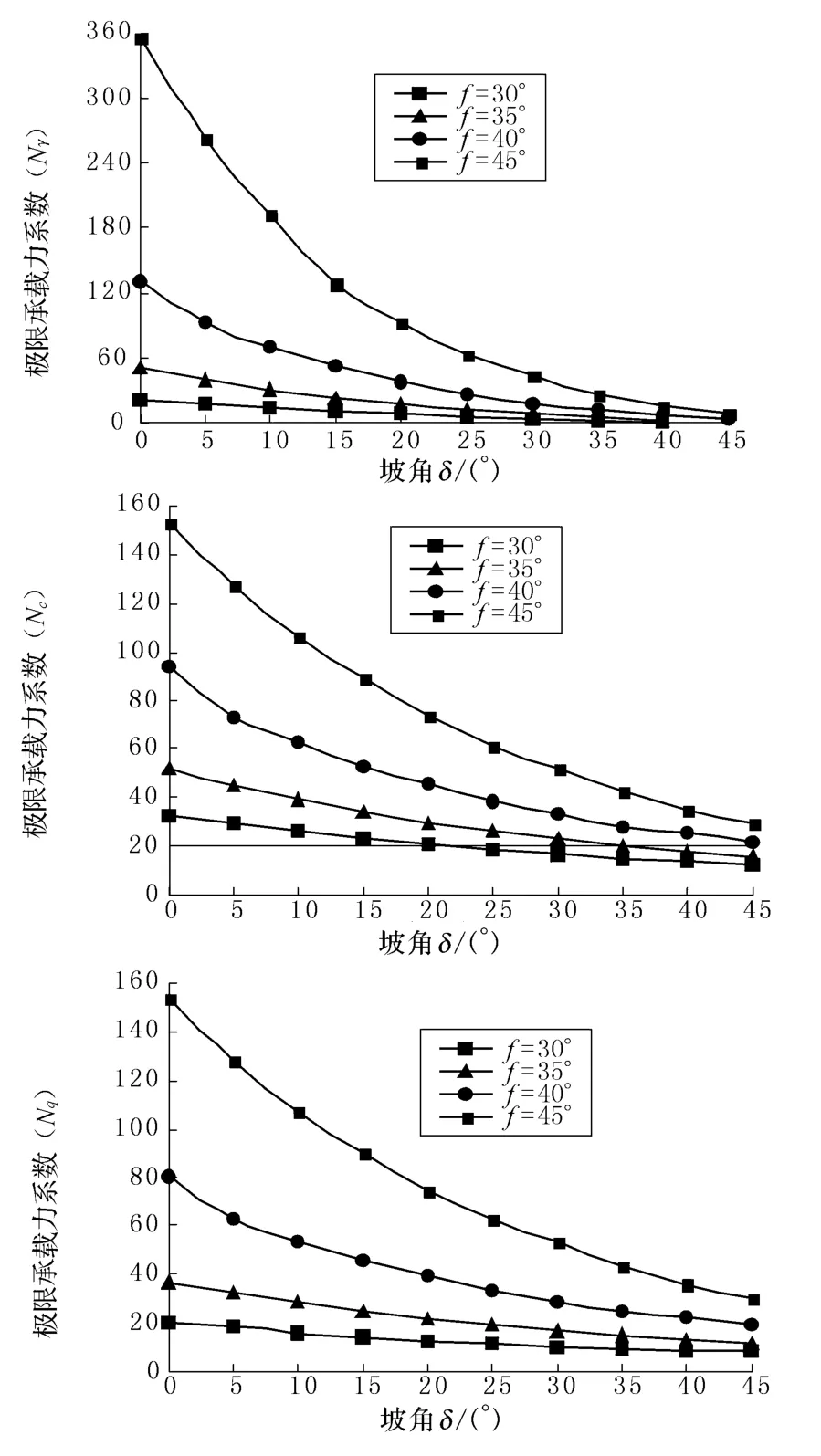
圖 8 Nγ,Nc,Nq隨δ變化情況

結(jié)合圖3,由圖7和圖8知:邊坡傾角的增加將使地基破壞區(qū)域發(fā)生顯著變化,使各分項系數(shù)呈非線性趨勢迅速減小,地基極限承載力顯著降低.邊坡的存在對臨坡地基穩(wěn)定性存在較大的不利影響,而巖土體內(nèi)摩擦角 φ提高將對提高地基承載力有利.因而在實際工程應(yīng)用中,可通過改良地基土物理力學(xué)特性或減緩邊坡坡角來提高基礎(chǔ)穩(wěn)定性.

4 結(jié) 論

1)計算中隨著剛性塊的增多,極限荷載將逐步減小并趨向于精確的解,且減小趨勢的變化率是迅速減小的.相同計算參數(shù)條件下,構(gòu)造剛性塊較少的簡單相容速度場也能夠求得較為精確的數(shù)值,因而計算的速度和效率也將得到大幅提高.

2)邊坡傾斜程度和地基巖土體內(nèi)摩擦角 φ對臨坡條形基礎(chǔ)地基承載力影響較大.邊坡坡角δ的增加將使地基破壞區(qū)域發(fā)生顯著變化,使極限承載力各分項系數(shù)Nγ,Nc,Nq迅速減小,地基極限承載力將減小;而內(nèi)摩擦角 φ增加對 Nγ,Nc,Nq的影響恰恰相反.因而在實際工程應(yīng)用中,可通過改良地基土物理力學(xué)特性或減緩邊坡坡角來提高基礎(chǔ)穩(wěn)定性.

3)將計算結(jié)果與已有文獻(xiàn)資料比較分析表明,所得結(jié)果較前人研究成果有一定改進(jìn).

[1]Saran S,Sud V K,H anda SC.Bearing capacity o f footings adjacent to slopes[J].Journal of Geotechnical Engineering,1989,115(4):553-573.

[2]酆慶增.臨近邊坡的基礎(chǔ)的極限承載力[J].力學(xué)季刊,1999,20(1):24-27.

[3]王紅雨,楊 敏.臨近基坑條形基礎(chǔ)地基承載力簡化上限解[J].同濟(jì)大學(xué)學(xué)報:自然科學(xué)版,2006,34(3):319-324.

[4]Yang X L,Wang Z B,Zou JF,etal.Bearing capacity o f foundation on slope determ ined by energy dissipationmethod andmodel experiments[J].Journalof Centra l South University of Technology,2007,14(1):125-128.

[5]趙 杰,邵龍?zhí)?土體結(jié)構(gòu)極限承載力的有限元分析[J].巖石力學(xué)與工程學(xué)報,2007,26(增刊1):3183-3189.

[6]李耘宇,胡曉敏,張嶸峰.地震液化對橋梁樁基礎(chǔ)極限承載力的影響[J].武漢理工大學(xué)學(xué)報:交通科學(xué)與工程版,2006,30(6):1044-1047.

[7] 趙煉恒,李 亮,楊 峰,等.基于SQP和上限法的非飽和土條形基礎(chǔ)極限承載力計算[J].巖石力學(xué)與工程學(xué)報,2009,28(增刊1):3021-3028.