一類極小的譜任意符號(hào)模式矩陣
荊亨通,邵燕靈
一類極小的譜任意符號(hào)模式矩陣
荊亨通,邵燕靈
(中北大學(xué)數(shù)學(xué)系,山西太原030051)
設(shè)A是一個(gè)n階符號(hào)模式,對(duì)任意首系數(shù)為1的n次實(shí)系數(shù)多項(xiàng)式f(x),若存在實(shí)矩陣B∈Q(A),使得B的特征多項(xiàng)式為f(x),則符號(hào)模式A為譜任意符號(hào)模式.本文運(yùn)用冪零-雅克比方法給出了一類極小譜任意符號(hào)模式矩陣.
符號(hào)模式;譜任意;冪零
0 引言
一個(gè)符號(hào)模式矩陣(簡稱符號(hào)模式)是元素取自集合{+,-,0}的矩陣.設(shè)A=(aij)是n階符號(hào)模式,則A的定性類定義為
Q(A)={B=(bij)|sign(bij)=aij,i,j=1,2,…,n}.對(duì)于符號(hào)模式S=(sij),若當(dāng)aij≠0時(shí),有sij=aij,則S為A的一個(gè)母模式,即A為S的一個(gè)子模式.A也為其自身的一個(gè)母模式.
若存在n階實(shí)矩陣B∈Q(A),使它的所有特征值為零,則稱B為符號(hào)模式A的一個(gè)冪零實(shí)現(xiàn).若A有冪零實(shí)現(xiàn),我們也可稱A是蘊(yùn)含冪零的.設(shè)A是一個(gè)n階符號(hào)模式,對(duì)任意首系數(shù)為1的n次實(shí)系數(shù)多項(xiàng)式f(x),若存在實(shí)矩陣B∈Q(A),使得B的特征多項(xiàng)式為f(x),則符號(hào)模式A為譜任意符號(hào)模式(SA P).任何譜任意符號(hào)模式一定是蘊(yùn)含冪零的.如果A是譜任意符號(hào)模式,而替換A中任何非零元后的符號(hào)模式矩陣不是譜任意的,則A為極小譜任意符號(hào)模式(MSAP).當(dāng)任意的B∈Q(A)為非奇異時(shí),A為符號(hào)非奇異的.
有關(guān)譜任意符號(hào)模式的研究開始于文獻(xiàn)[1],且給出了證明譜任意符號(hào)模式的方法.隨后文獻(xiàn)[2-5]給出并證明了一些符號(hào)模式是譜任意的.本文給出一類n階符號(hào)模式Dn并證明它是譜任意的.
引理1.1[1]A是一個(gè)n階符號(hào)模式,假設(shè)存在冪零實(shí)現(xiàn)B∈Q(A),且B中到少有n個(gè)非零元bi1j1,…, binjn.令X為用變量(x1,…,xn)代替B中bi1j1,…,binjn后得到的矩陣,且令
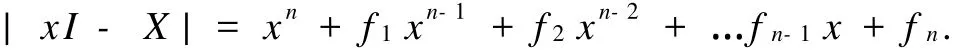
若X的特征多項(xiàng)式的系數(shù)對(duì)于變量(x1,…,xn)的雅克比行列式在(x1,x2,…,xn) =(bi1j1,bi2j2,…,binjn)處不為零,那么A的任何母模式均為譜任意符號(hào)模式.
1 符號(hào)模式Dn
本文討論以下n階符號(hào)模式其中第n-2行和第n-1行的“-”元素分別位于第r1列和第r2列,且n≥6.

取

其中ai>0,i=1,2,…,n.令a0=1.
令A(yù)n的特征多項(xiàng)式為
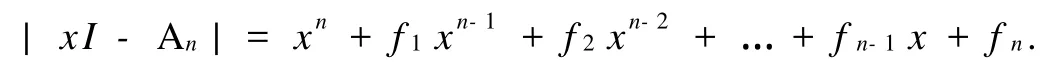
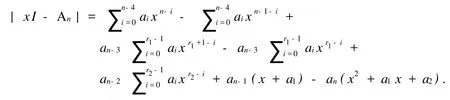
從最后一行展開|x I-An|,并由引理1.1可推出定理1.1 若3≤r2 證明 容易算出An的特征多項(xiàng)式各項(xiàng)的系數(shù)為 令fi=0,得到 容易算出,在冪零點(diǎn)處J=1-r2≠0.由引理1.1可知該定理成立,即證. 定理1.2 若2≤r1 證明 容易算出An的特征多項(xiàng)式各項(xiàng)的系數(shù)為 令其系數(shù)fi=0,可得到故Dn有冪零實(shí)現(xiàn). 同樣可得出雅克比行列式在冪零點(diǎn)處等于1-r2.即證. 定理1.3 若r1=r2=r,且2≤r≤.那Dm的任何母模式都是譜任意的. 證明 容易算出An的特征多項(xiàng)式各項(xiàng)的系數(shù)為 通過求解fi=0,(i=1,2,…,n)可知當(dāng)時(shí),An是Dn的冪零實(shí)現(xiàn). 此時(shí)可得到在冪零點(diǎn)處J=1-r≠0,即證, 定理1.4 若r1=1,且3≤r2=r≤,那么Dn的任何母模式都是譜任意的. 證明 容易算出An的特征多項(xiàng)式各項(xiàng)的系數(shù)為 令其系數(shù)fi=0,有,故Dn有冪零實(shí)現(xiàn). 雅克比行列式J在冪零點(diǎn)處等于2-r≠0.即證. 引理1.2[3]n階不可約譜任意符號(hào)模式至少有2n-1個(gè)非零元. 定理1.5 符號(hào)模式Dn在定理1.1-1.4的條件下為極小譜任意符號(hào)模式. 證明 假設(shè)S=[sij]為Dn的一個(gè)子模式,且S為譜任意符號(hào)模式,則 (1)s1,1≠0,且sn-1,n-1≠0,否則S的跡為非負(fù)或非正. (2)si,i+1≠0(i=1,2,…,n-1),否則S為符號(hào)非奇異或符號(hào)奇異的. (3)sn-2,r1≠0,sn-1,r2≠0.sn,2≠0,且sn,3≠0,因?yàn)榇嬖趯?shí)矩陣A∈Q(S)使得A是冪零的,且得到an-3= an-2=an-1=an.若an-3=an-2=an-1=an=0,那么S中的非零元個(gè)數(shù)少于2n-1,即S不是譜任意的. (4)si,1≠0(i=2,3,…,n-r-1,r=max{r1,r2}),否則xn-i的系數(shù)不是任意的. (5)si,1≠0(i=n-r,n-r+1,…,n-4),否則與(3)矛盾. 因此,S=Dn,故Dn為極小譜任意符號(hào)模式.證畢. 證明 容易得出An的特征多項(xiàng)式各項(xiàng)的系數(shù)為 fi=ai-ai-1,i=1,2,…,n-r1-2, fi=an-3ai-n+r1+1-an-3ai-n+r1+ai-ai-1,i=n-r1-1,n-r1,…,n-4. fn-3=an-3ar1-2-an-3ar1-3-an-4, fn-2=an-3ar1-1-an-3ar1-2-an, fn-1=-an-3ar1-1+an-2+an-1-ana1, fn=an-1a1-ana2. 令fi=0,i=1,2,…,n,由fi=0,i=1,2,…,n-r1-2,得到a1=a2=…=an-r1-2=1.由fn=fn-1=fn-2=fn-3=0,有an=an-1=an-2=an-3=an-4=0.由fn-4=fn-5=…=fn-r1-1,能得到an-5=an-6=…= an-r1-1=0.與ai>0矛盾,故Dn不蘊(yùn)含冪零. 證明 容易算出An的特征多項(xiàng)式各項(xiàng)的系數(shù)為 fi=ai-ai-1,i=1,2,…,n-r1-2, fi=an-3ai-n+r1+1-an-3ai-n+r1+ai-ai-1,i=n-r1-1,n-r1,…,n-4. fn-3=an-3ar1-2-an-3ar1-3-an-4, fn-2=an-3ar1-1-an-3ar1-2+an-2-an, fn-1=-an-3ar1-1+an-2a1+an-1-ana1, fn=an-1a1-ana2. 令fi=0,i=1,2,…,n,由fi=0,i=1,2,…,n-r1-2,得到a1=a2=…=an-r1-2=1.由fn-3=0,有an-4=0.由fn-4=fn-5=…=fn-r1=0,能得到an-4=an-5=…=an-r1-1=0.與ai>0矛盾,故Dn不是蘊(yùn)含冪零的. [1] DREW J H,JOHNSON C R,OL ESKYD D,et al.Spectrally Arbitrary Patterns[J].Linear A lgebra A ppl,2000,38:121-137. [2] MCDONALD J J,OL ESKY D D,TSATSOMEROS M J,et al.On the Spectra of Striped sign Patterns[J].Linear Multilinear A lgebra,2003,51(1):39-48. [3] CAVERS M S,VANER K N MEUL EN.Spectrally and inertially Arbitrary Sign Patterns[J].Linear A lgebra A ppl, 2005,394:53-72. [4] BRITZ T,MCDONALD J J,OLESKY D D,et al.Minimal Spectrally Arbitrary Sign Patterns[J].S IA M J Matrix A nal A ppl,2004,26(1):257-271. [5] CAVERS M S,KIM I J,SHADER B L,et al.On Determining Minimal Spectrally Arbitrary Patterns[J].Elec J L inear A lgebra,2005,13:240-248. [6] SHAO Yan-ling,GAO Yu-bin.Maximal Inertially Arbitrary Patterns[J].N umerical Mathematics A J ournal of Chinese Universities.2003,12:99-102. [7] LI Xi,SHAO Yan-ling,GAO Yu-bin.A Class of Minimally Spectrally Arbitrary Sign Patterns[J].A rs Combinatoria Inpress. [8] GAO Yu-bin,SHAO Yan-ling.Inertia sets of Symmetric 2-generalized star Sign Patterns[J].Linear and Multilinear A lgebra,2006,54:27-35. [9] MACGILLIVRAY G,TIFENBACH R M,van den DRIESSCHE P.Spectrally Arbitrary Star Sign Patterns[J].Linear A lgebra A ppl,2005,400:99-119. A New Class of Minimal Spectrally Arbitrary Sign Patterns J ING Heng-tong,SHAO Yan-ling Let a sign patternAof ordernis a spectrally arbitray pattern.If for every monic polynomialf(x) of degreenthere is a real matrixB∈Q(A)so that the characteristic polynomial ofBisf(x),Ais known as a spectrally arbitray pattern.In this paper,by using Nilpotent-Jacobian method,a new class of spectrally arbitrary sign patterns is presented,which is proved also to be minimal spectrally arbitrary sign patterns. sign pattern;spectrally arbitrary sign pattern;potentially nilpotent O157.5 A 0253-2395(2010)03-0343-06 2009-09-10; 2010-05-11 山西省然科學(xué)基金(2007011017;2008011009) 荊亨通(1964-),男,碩士研究生,主要從事組合數(shù)學(xué)研究.E-mail:jinghengtong-123@163.com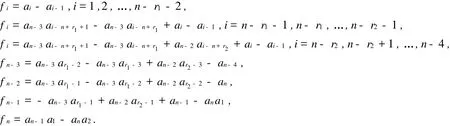
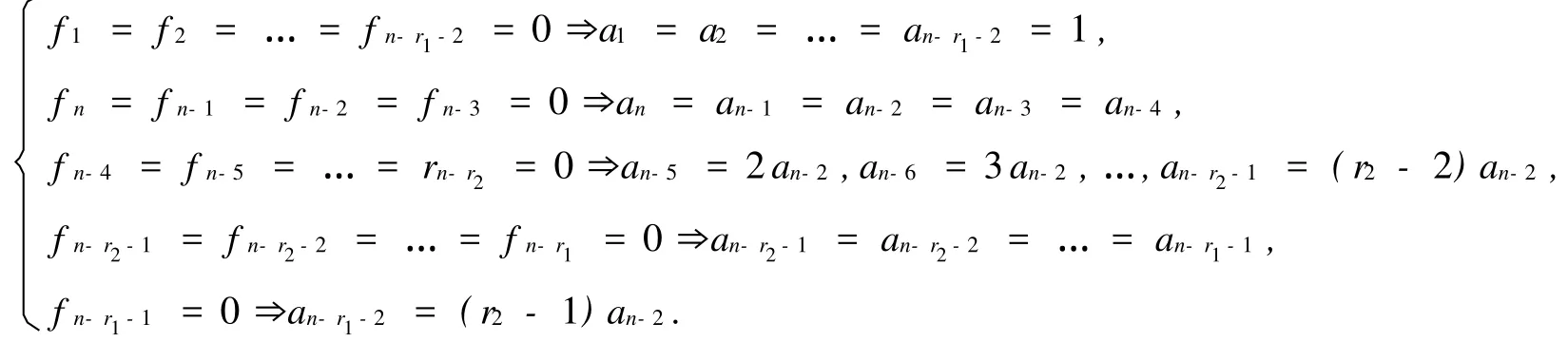

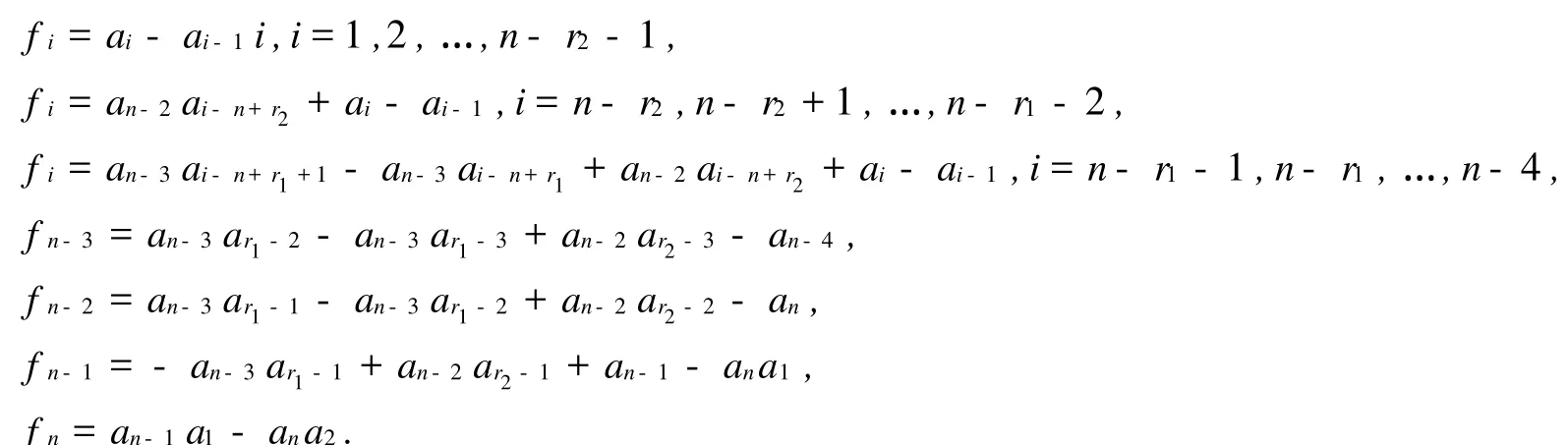

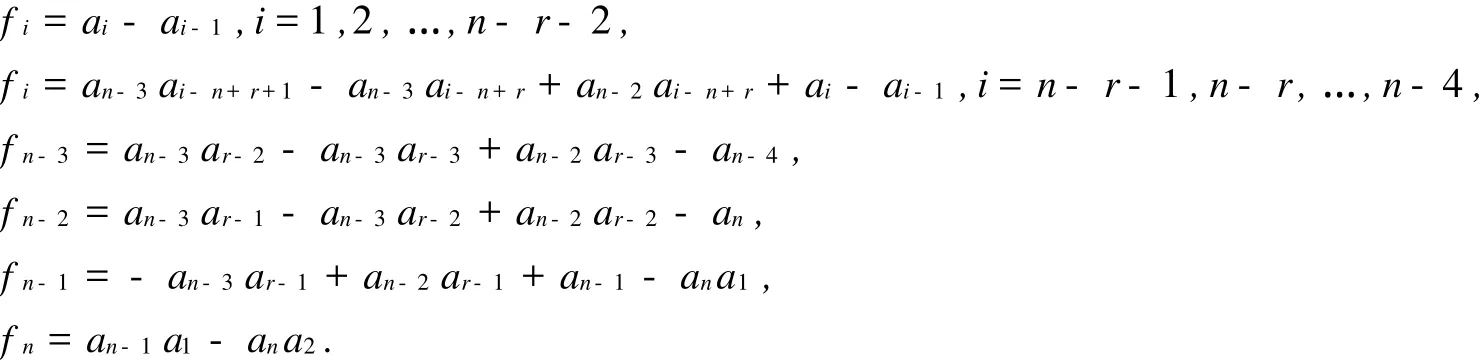

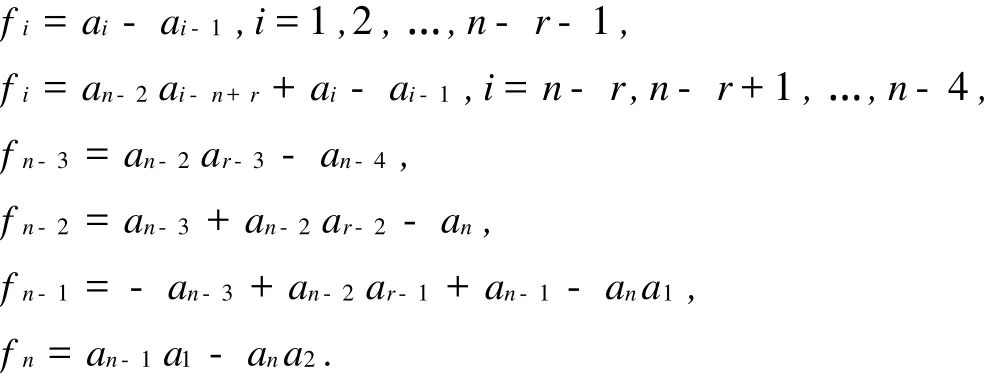

(Deptartment of Mathematics,North University of China,Taiyuan030051,China)

