梅銀珍,高玉斌

一類非冪零極小慣量任意符號(hào)模式矩陣

梅銀珍,高玉斌

(中北大學(xué)數(shù)學(xué)系,山西太原030051)

如果一個(gè)慣量任意符號(hào)模式的任意一個(gè)或多個(gè)非零元被零取代后所得到的符號(hào)模式不是慣量任意的,則這個(gè)慣量任意符號(hào)模式稱為極小慣量任意符號(hào)模式(MIAP).文獻(xiàn)[1]中In-Jac Kim等給出一類不可約的慣量任意符號(hào)模式ψ2k+1(k≥2),并證明了當(dāng)k=2,3時(shí)是(MIAP).文章將證明k≥4時(shí)ψ2k+1也是(MIAP).

符號(hào)模式;慣量任意;極小慣量任意

0 引言

符號(hào)模式矩陣是指元素取自集合{+,-,0}或{1,-1,0}的矩陣,簡(jiǎn)稱為符號(hào)模式.用Qn表示全體n階符號(hào)模式所組成的集合.對(duì)任意S∈Qn,所有與S有相同符號(hào)模式的實(shí)矩陣組成的集合

{A∈Mn(R)|sign(aij)=sij,?i,j∈{1,2,…,n}},稱為由S所決定的定性矩陣類,記為Q(S).如果H=S或H是由S中的一個(gè)或多個(gè)非零元被零替換后所得到的,那么稱H為n階模式S的子模式,也稱S為H的母模式.當(dāng)H≠S時(shí),稱H為S的真子模式,S為H的真母模式.如果對(duì)于任意一個(gè)滿足n1+n2+n3=n的非負(fù)三元整數(shù)組(n1,n2,n3),都存在一個(gè)實(shí)矩陣M∈Q(S),使得i(M)=(n1,n2,n3),則稱符號(hào)模式S是慣量任意的[1,4-7],記為IAP.如果S的任意一個(gè)真子模式均不是IAP.則稱符號(hào)模式S是極小慣量任意符號(hào)模式[2,3],記為MIAP.

設(shè)2k+1階符號(hào)模式

文獻(xiàn)[1]中,作者證明了S2k+1(k≥2)是慣量任意符號(hào)模式,且S5,S7是極小慣量任意符號(hào)模式,并猜想S2k+1(k≥4)也是極小慣量任意符號(hào)模式矩陣.本文論證了k≥4時(shí)該猜想是正確的.

1 一些引理

設(shè)k≥2,

其中aj,bj,cj,dj是正的或零.記A2k+1的特征多項(xiàng)式為

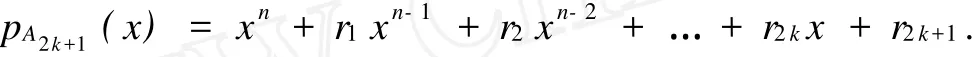
經(jīng)過(guò)計(jì)算得到

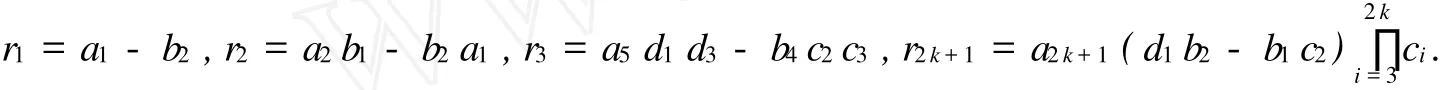
顯然有如下結(jié)論:

(1)若a1和b2有一為零,則A2k+1的跡或負(fù)或正,那么A2k+1取不到慣量(0,0,2k+1);

(2)若a2k+1,ci(i=3,…,2k)至少有一為零,則r2k+1=0,那么A2k+1取不到慣量(0,2k+1,0);

(3)若a2,b1至少有一為零,則r2≤0,由韋達(dá)定理知A2k+1取不到慣量(2k+1,0,0);

(4)若d1為零,則r2k+1≤0,A2k+1不能取到慣量(0,2k+1,0);

(5)若c2為零,則r2k+1>0,A2k+1不能取到慣量(0,0,2k+1);

(6)若a5和d3有一為零,則r3≤0,A2k+1不能取到慣量(0,2k+1,0);

(7)若b4為零,則r3>0,A2k+1不能取到慣量(2k+1,0,0).

綜合上述討論,有以下引理.

引理1 設(shè)k≥2,U2k+1是S2k+1的一個(gè)子模式,且U2k+1是慣量任意符號(hào)模式,A2k+1∈Q(U2k+1),則ci≠0 (i=2,3,…,2k),di≠0(i=1,3),bi≠0(i=1,2,4),ai≠0(i=1,2,5,2k+1).

引理2 設(shè)B是n階實(shí)矩陣,pB(x)=xn+r1xn-1+r2xn-2+…+rn-1x+rn是B的特征多項(xiàng)式.若i(B) =(0,n,0),則rj>0,j=1,…,n.

引理3[1]符號(hào)模式ψ5和ψ7是MIAP.

引理4[1]當(dāng)k≥2時(shí),若A2k+1恰有一個(gè)零特征值,則矩陣A2k+1的元素a2,b2,c2滿足以下條件之一:

(i)a2=a1+a2k+1,b2=b1,c2=d1;

(ii)a2=a1-a2k+1,b2=b1,c2=d1;

(iii)a2=a1,b2=b1,c2=d1.

證明 若A2k+1恰有一個(gè)零特征值,則齊次線性方程組XA2k+1=O有非零解τ,即τA2k+1=O.令τ=(x1, x2,…,x2k+1)且令

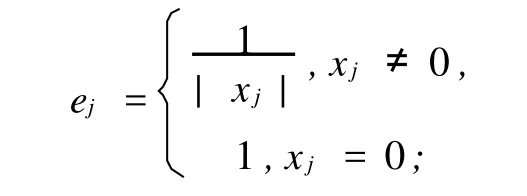
那么D=diag(e1,…,e2k+1)是對(duì)角元為正的對(duì)角矩陣,且對(duì)于每個(gè)j=1,…,2k+1時(shí),有(τD)j∈{1,-1,0}.由τA2k+1=O,得到τDD-1A2k+1D=O.令v=τD=v=(v1,…,v2k+1)且A=D-1A2k+1D.那么A∈Q(S2k+1),vA =0(vj∈{1,-1,0}).因?yàn)閷?duì)于每個(gè)j=3,5,…,2k-1時(shí),-cj是A2k+1的第j+1列的唯一非零元,得到當(dāng)j =3,5,…,2k-1時(shí),vj=0成立.對(duì)于每個(gè)j=4,6,…,2k,考慮(vA)j+1,對(duì)于每個(gè)j=4,6,…,2k時(shí),有vj= 0.因?yàn)関1=0且v2=0,因此v2k+1=0,得到了v1∈{1,-1}.假設(shè)v1=1.那么由(vA)3=0就可以得到v2=1.因此,不失一般性,左乘A的非零向量v是下面的向量(i),(ii)和(iii)中的一個(gè):

(i)(1,1,0,…,0,1),(ii)(1,1,0,…,0,-1);(iii)(1,1,0,…,0).

如果向量v是(i),(ii)或(iii),那么矩陣A2k+1的元素a2,b2,c2分別如下:

(i)a2=a1+a2k+1,b2=b1,c2=d1;

(ii)a2=a1-a2k+1,b2=b1,c2=d1;

(iii)a2=a1,b2=b1,c2=d1.

證畢.

2 主要結(jié)論

由于相似矩陣的特征值相同,由引理1可不妨設(shè)A2k+1有以下形式

其中aj,bj,dj是正的或零.記A1是矩陣A滿足引理4(i)的矩陣.

引理5 設(shè)i(A1)=(0,2k,1),則a2j+1≠0,b2j≠0(j=3,…,k-1),d2j+1≠0(j=2,…,k-2).

證明 設(shè)i(A1)=(0,2k,1),則r2k+1=0,再由引理2知rj>0,j=1,…,2k.經(jīng)過(guò)計(jì)算得到

其中di,dij∈{d3,d5,d7,…,d2k-3},表示所有互不相同且滿足s≤i,j≤m的h個(gè)dij乘積之和.

e1=a2k+1d2k-1-b2k,e2=a2k-1d2k-3-b2k-2,…,ei=a2k-2i+3d2k-2i+1-b2k-2i+2,…,ek-4=a11d9-b10,ek-3= a9d7-b8,ek-2=a7d5-b6;

f1=a2k+1b2k-a2k+1,f2=a2k+1b2k-2-a2k-1,…,fi=a2k+1b2k-2i+2-a2k-2i+3,…,fk-4=a2k+1b10-a11,fk-3=a2k+1b8-a9,fk-2=a2k+1b6-a7,fk-1=a2k+1b4-a5.

由rj>0,j=1,…,2k易知ej>0,j=1,…,k-2;fj>0,j=1,…,k-1.

下證a2j+1(j=3,…,k-1),b2j(j=3,…,k-1),d2j+1(j=2,…,k-2)都不可能為0.否則:

若a2j+1=0(j=3,…,k-1),則ei=a2k-2i+3d2k-2i+1=-b2k-2i+2<0,矛盾;

若d2j+1=0(j=2,…,k-2),則ei=a2k-2i+3d2k-2i+1=-b2k-2i+2<0,矛盾;

若b2j=0(j=3,…,k-1),則fi=a2k+1b2k-2i+2-a2k-2i+3=-a2k-2i+3<0,矛盾.

證畢.

定理 S2k+1(k≥4)是極小慣量任意符號(hào)模式(MIAP).

證明 設(shè)U2k+1是S2k+1的一個(gè)子模式,且U2k+1是慣量任意的.又設(shè)A∈Q(S2k+1),且i(A)=(0,2k,1),即A恰有一個(gè)零特征值,由引理4知A的元素必是以下三種情形之一:

(i)a2=a1+a11,b2=1,d1=1; (ii)a2=a1-a11,b2=1,d1=1; (iii)a2=a1,b2=1,d1=1.

而此時(shí)由引理2得rj>0,j=1,…,2k.對(duì)于(ii)的情形,有r2=-a2k<0,對(duì)于(iii)的情形,有r2=0.矛盾,故A一定是如情形(i)的矩陣A1.由引理5知,a2j+1≠0(j=3,…,k-1),b2j≠0(j=3,…,k-1),d2j+1≠0 (j=2,…,k-2).

綜上,我們可知U2k+1即S2k+1是極小慣量任意符號(hào)模式.證畢.

[1] KIM IJ,OL ESKYD D,DRIESSCHE P van den.Inertially arbitrary sign patterns with no nilpotent realization[J].Linear A lgebra and its A pplications,2007,421:264-283.

[2] BRITZ T,MCDONALD J J,OL ESKY D D,et al.Minimal Spectrally Arbitrary Sign Patterns[J].S IA M J Matrix A nal A ppl,2004,26:257-271.

[3] CAVERS M S,KIM B L,SHANER K N.On Determining Minimal Spectrally Arbitrary Patterns[J].Elec J Linear A lgebra,2005,13:240-248.

[4] CAVERS M S,VANDER MEUL EN K N.Spectrally and Inertially Arbitrary Sign Patterns[J].Linear A lgebra A ppl, 2005,394:53-72.

[5] GAO Yu-bin,SHAO Yan-ling.Inertially Arbitrary Patterns[J].Linear Multilinear A lgebra,2001,49:161-168.

[6] CORPUZ L,MCDONALD J J.Spectrally Arbitrary Zero Nonzero Patterns of Order 4[J].Linear and Multilinear A lgebra,2007,55:249-273.

[7] DREW J H,JOHNSON C,OL ESKY D D,et al.Spectrally Arbitrary Patterns[J].L inear A lgebra A ppl,2000,308:121-

137.

A Class of Minimal Inertially Arbitrary Sign Patterns with No Nilpotent

MEI Yin-zhen,GAO Yu-bin
(Department of Mathematics,North China University,Taiyuan030051,China)

A sign patternSis minimal inertially arbitrary if it is not inertially arbitrary when any one or more nonzero entries ofSis replaced by zero.In[1]In-Jac Kim,et al proved aD.D.Olesky famliy of irreducible inertially arbitrary sign patternsψ2k+1(k≥2),and showed thatψ5andψ7are minimal inertially arbitrary.In this paper,it is proved thatψ2k+1(k≥4)are also minimally inertially arbitrary.

sign pattern;inertia arbitrary;minimal inertially arbitrary

O157.5

A

0253-2395(2010)03-0339-04

2009-11-30;

2010-03-10

國(guó)家自然科學(xué)基金(10571163);山西省自然科學(xué)基金(2007011017)

梅銀珍(1977-),女,山西原平人,講師,在讀博士,主要從事組合數(shù)學(xué)研究.