一維反鐵磁海森堡系統(tǒng)的磁化強(qiáng)度
李素艷,李詠梅
(1.泰山學(xué)院物理與電子工程學(xué)院,山東泰安 271021;2.濟(jì)寧學(xué)院物理與信息工程系,山東曲阜 273155)
一維反鐵磁海森堡系統(tǒng)的磁化強(qiáng)度
李素艷1,李詠梅2
(1.泰山學(xué)院物理與電子工程學(xué)院,山東泰安 271021;2.濟(jì)寧學(xué)院物理與信息工程系,山東曲阜 273155)
利用數(shù)值密度矩陣重正化群方法研究了一維反鐵磁海森堡系統(tǒng)的磁化曲線,分析了不同阻挫時(shí)的磁化特性,著重描述了磁化曲線中出現(xiàn)的中場(chǎng)尖奇點(diǎn),并分析其產(chǎn)生機(jī)理.
密度矩陣重正化群;海森堡系統(tǒng);磁化曲線;中場(chǎng)尖奇點(diǎn)
0 引言
傳統(tǒng)數(shù)值重正化群(RG)方法是由W ilson在求解近藤(Kondo)問(wèn)題時(shí)提出的[1],它克服了完全對(duì)角化方法的局限性,但由于假定只有最低“塊”本征態(tài)與最終(無(wú)限)系統(tǒng)的基態(tài)有關(guān),故對(duì)邊界條件處理不理想.W hite進(jìn)而提出了密度矩陣重正化群(DMRG)方法[2-3],該方法是用密度矩陣的本征態(tài)代替以往直接使用“小塊”哈密頓量的本征態(tài)作為保留態(tài).對(duì)一維和準(zhǔn)一維問(wèn)題,這種方法得到的結(jié)果相當(dāng)準(zhǔn)確.同時(shí),相對(duì)于嚴(yán)格對(duì)角化方法,可以完成大尺寸系統(tǒng)的計(jì)算.鑒于以上優(yōu)點(diǎn),密度矩陣重正化群方法現(xiàn)已被證明是研究一維和準(zhǔn)一維量子系統(tǒng)的有力工具.
1 密度矩陣重正化群算法
密度矩陣重正化群算法如下[4]:
(1)構(gòu)造4個(gè)初始“塊”,第一(左邊)“塊”包含一個(gè)或多個(gè)格點(diǎn),第二、第三“塊”由單個(gè)格點(diǎn)組成,第四(右邊)“塊”是第一“塊”的空間反射.
(2)構(gòu)造超級(jí)“塊”的哈密頓矩陣Hsuper.
(3)通過(guò)稀疏矩陣對(duì)角化方法如Davidson[5]或Lanczos算法[6](本文應(yīng)用Lanczos算法)對(duì)角化Hsuper得到靶態(tài)ψ即超級(jí)“塊”的基態(tài).
(5)對(duì)角化ρ得到所有本征矢vα及本征值aα,保留m個(gè)最大的本征值及相應(yīng)的本征矢,其余舍去.
(6)對(duì)兩“塊”系統(tǒng)的活躍(位于端點(diǎn)處的)自旋算符構(gòu)造矩陣表象.
(7)利用方程H1’=OH12OT將基變?yōu)関α,產(chǎn)生新“塊”1.同樣變換步驟6中的算符.
(8)用新“塊”1代替舊“塊”1,新“塊”1的反射代替舊“塊”4.
(9)回到步驟2,重復(fù)以上步驟直到收斂.
密度矩陣重正化群方法結(jié)構(gòu)見(jiàn)圖1,在每一次迭代中,超級(jí)“塊”增加兩個(gè)格點(diǎn),而基態(tài)數(shù)不變.計(jì)算出的性質(zhì)收斂到其熱力學(xué)極限值.
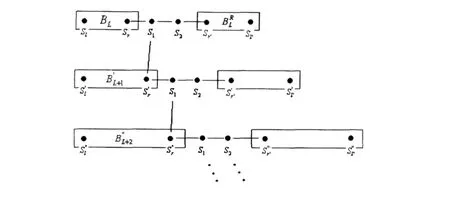
圖1 密度矩陣重正化群方法結(jié)構(gòu)示意圖
以上算法的關(guān)鍵步驟在于超級(jí)“塊”哈密頓量的存儲(chǔ)及對(duì)角化.顯然,矩陣Hsuper由(4m2)2個(gè)元素構(gòu)成.幸而大部分矩陣元為零,僅需存儲(chǔ)不為零的矩陣元.另外,“塊”對(duì)角化的矩陣可以一“塊”一“塊”地對(duì)角化,從而比一次對(duì)角化整個(gè)矩陣節(jié)省CPU.本文中計(jì)算磁化曲線,我們僅計(jì)算對(duì)應(yīng)于某特定磁化強(qiáng)度的最低的能量,這樣每次只需考慮對(duì)應(yīng)于該磁化強(qiáng)度的矩陣元.
以上算法為無(wú)限大小算法,超級(jí)“塊”隨每一次迭代而增加,故一般用以計(jì)算熱力學(xué)極限時(shí)的量.該算法可被擴(kuò)展提高其精確度以計(jì)算固定長(zhǎng)度L的有限系統(tǒng).首先我們應(yīng)用無(wú)限大小算法直到超級(jí)“塊”達(dá)到所需長(zhǎng)度L.在之后的迭代中由兩個(gè)長(zhǎng)度不同的次級(jí)“塊”生成一個(gè)具有固定長(zhǎng)度的超級(jí)“塊”.如果左邊“塊”代表一個(gè)L’格點(diǎn)的系統(tǒng)(這里我們選L’=L/2),加上兩個(gè)格點(diǎn),再與一個(gè)L-L’-2格點(diǎn)“塊”(無(wú)限大小方法得到的L-L’-2格點(diǎn)“塊”的反射)連接就構(gòu)成一個(gè)超級(jí)“塊”.該L-L’-2格點(diǎn)系統(tǒng)的哈密頓矩陣及每個(gè)必須的算符都來(lái)自于前一迭代.每一步中,我們構(gòu)造L格點(diǎn)超級(jí)“塊”,而次級(jí)“塊”的大小從長(zhǎng)度Lmin變到L-Lmin-2.該過(guò)程經(jīng)過(guò)迭代,左邊次級(jí)“塊”增大,右邊次級(jí)“塊”取自前面的迭代.
密度矩陣重正化群方法的總體誤差取決于每次迭代保留的態(tài)數(shù)及系統(tǒng)大小.另外還取決于研究的模型,特別是相互作用范圍及邊界條件.當(dāng)重正化“塊”與超級(jí)“塊”其余部分間的連接最小化時(shí),精確度最高.在無(wú)限大小算法中,該誤差源于超級(jí)“塊”的其余部分,即反射“塊”被假定代表無(wú)限鏈的其余部分.自由邊界條件時(shí)得到的結(jié)果優(yōu)于周期性邊界條件的結(jié)果,原因在于周期性邊界條件時(shí)“塊”與反射“塊”間有兩個(gè)連接,而自由邊界條件時(shí)只有一個(gè)連接.
無(wú)限大小方法中,在迭代的固定點(diǎn),“塊”B代表無(wú)限鏈的一半.通常從中得到的有限鏈結(jié)果是有用的,但這樣得到的結(jié)果不是十分準(zhǔn)確.原因在于最初所用密度矩陣是從非常小的晶格中得到的.另外,有限大小方法適用于有限系統(tǒng).通過(guò)有限大小方法,初始誤差被隨后的掃描減小.


2 磁化曲線
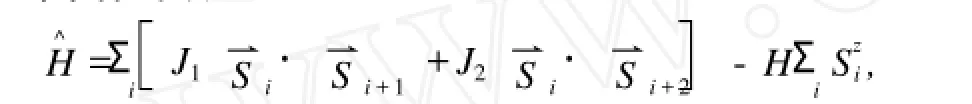
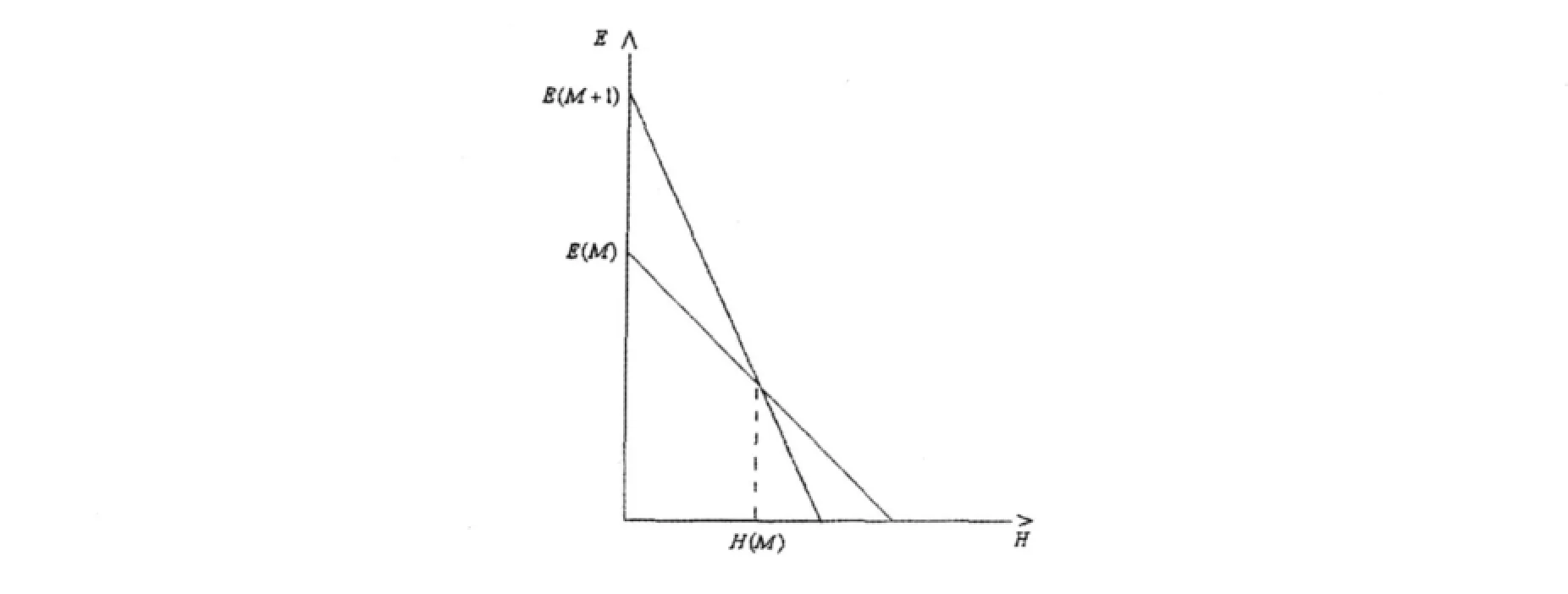
圖3 E-H曲線
易發(fā)現(xiàn)E(M)-E(M?1)=±H.
故對(duì)給定的M,我們有H=E(M)-E(M-1),或H=E(M+1)-E(M).
對(duì)每個(gè)磁化強(qiáng)度M,存在著相應(yīng)的外場(chǎng),連接這些點(diǎn)可得到M-H曲線.計(jì)算對(duì)磁化強(qiáng)度為M的L格點(diǎn)系統(tǒng)的最低能量E(M),繼而通過(guò)確定E(M)與E(M±1)的水平交點(diǎn)即可得到磁化曲線.
3 結(jié)果與分析
AF自旋鏈的磁化過(guò)程表現(xiàn)出各種類(lèi)相變特性:伴隨著間隙激發(fā)(激發(fā)間隙∝Hc)或飽和磁化(在飽和場(chǎng)Hs)的臨界現(xiàn)象以及相變.在M-H曲線上還存在著中場(chǎng)尖奇點(diǎn).尖奇點(diǎn)出現(xiàn)于中場(chǎng)區(qū)H=Hcusp處,其中Hc 圖4 20格點(diǎn)AF鏈M-H曲線 在圖4中,我們得出一個(gè)20格點(diǎn)AF自旋鏈的M-H曲線,其中α分別為0,0.25,0.35.從圖中我們可以清楚地看見(jiàn)M-H曲線在三個(gè)不同阻挫的大體輪廓.可以觀察到α=0的平方根特性,以及α= 0.25的四次方根特性.對(duì)α=0.35,可以看到在H接近于2.0處有一個(gè)尖. 在αc≈0.241167的地方有相變產(chǎn)生.當(dāng)α<αc時(shí),基態(tài)是無(wú)間隙的自旋流體相.當(dāng)α>αc時(shí),基態(tài)變成具有一定間隙的d im er相.自旋流體相和dim er相在長(zhǎng)程有序上的區(qū)別對(duì)M(α,H)磁化曲線有明顯影響. 由上圖及其他參考文獻(xiàn)中可知α=0.1,0.2及0.25在中場(chǎng)區(qū)域沒(méi)有反常結(jié)構(gòu).α=0.35,0.4及0.5的M-H曲線在H接近于飽和場(chǎng)的地方有中場(chǎng)尖奇點(diǎn).Okunishi證明對(duì)α=0.6,零溫M-H曲線有兩個(gè)中場(chǎng)尖奇點(diǎn).另外,我們發(fā)現(xiàn)盡管阻挫不同,飽和場(chǎng)卻彼此接近.原因在于一個(gè)具有一維AF競(jìng)爭(zhēng)性近鄰及次近鄰系統(tǒng)相互作用系統(tǒng)的飽和場(chǎng)主要由最近鄰決定.Tonegw a與Harada計(jì)算了具有反鐵磁近鄰及次近鄰相互作用的一維各向同性自旋1/2海森堡AF的飽和場(chǎng).根據(jù)他們的結(jié)果,次近鄰相互作用對(duì)飽和場(chǎng)的修正非常小,即便是在象R iera和Dobry的計(jì)算中,次近鄰相互作用相當(dāng)大時(shí)也是如此.然而,對(duì)一個(gè)具有近鄰和次近鄰相互作用的自旋-佩爾斯系統(tǒng),如果沒(méi)有令人滿(mǎn)意的磁化曲線理論,僅靠當(dāng)前的實(shí)驗(yàn)數(shù)據(jù)很難對(duì)次近鄰相互作用做定量的估計(jì). 我們還發(fā)現(xiàn)對(duì)小的阻挫,在對(duì)小外場(chǎng)M和H之間存在線性關(guān)系.對(duì)α≥0.5,不消失的磁化強(qiáng)度要求外場(chǎng)超過(guò)臨界值HC(α). 已經(jīng)證實(shí)Z字形鏈當(dāng)改變?chǔ)習(xí)r具有有趣的M-H曲線.這是什么導(dǎo)致的呢?Okunishi認(rèn)為這個(gè)問(wèn)題可以當(dāng)作一個(gè)無(wú)自旋費(fèi)米氣體來(lái)處理,其中費(fèi)米子相當(dāng)于鐵磁背景下翻轉(zhuǎn)的自旋. 接近于Hs處,α≤0.25的系統(tǒng)是費(fèi)米液體.因此對(duì)α>0.25,我們預(yù)期系統(tǒng)將繼續(xù)表現(xiàn)為費(fèi)米液體.定性地分析,費(fèi)米液體特征也能成功地解釋M-H曲線,尤其是中場(chǎng)尖奇點(diǎn)的出現(xiàn).定量地討論,卻出現(xiàn)了與α≤0.25時(shí)重要的不同.該系統(tǒng)成為兩種成分的液體,每部分由極小值周?chē)哪=M成.這樣一個(gè)相關(guān)多組分系統(tǒng)可能表現(xiàn)為非費(fèi)米液體,或Tomonaga-Lu ttinger(TL)液體,它的典型例子是Hubbard鏈. 以上我們研究了一維反鐵磁系統(tǒng)的零溫磁化過(guò)程(M-H曲線).該磁化過(guò)程展示出各種相變特性.接近飽和場(chǎng),對(duì)α>0.25存在中場(chǎng)尖奇點(diǎn),可觀察到相關(guān)的雙組分TL液體特性,該處元激發(fā)色散曲線是雙阱曲線.在α=0.25,M-H曲線表現(xiàn)為△M~(H-Hs)1/4與α<0.25時(shí)的平方根行為不同.存在中場(chǎng)尖奇點(diǎn)的本質(zhì)機(jī)制在于低激發(fā)態(tài)能量的多極小值結(jié)構(gòu). [1]W ilson K G.The renorm alization group:Criticalphenom ena and the Kondo p roblem[J].RevMod Phys,1975,47:773-840. [2]W h ite SR,Noack R M.Real-space quan tum reno rm a lization g roup s[J].PhysRev Lett,1992,68:3487-3490. [3]W h ite SR.Densitym atrix formulation for quantum renorm alization groups[J].PhysRev Lett,1992,69:2863-2866. [4]W h ite SR.Densitym atrix algo rithm s for quan tum reno rm alization group s[J].Phys Rev B,1993,48:10345-10356. [5]Davidson E R.The iterative calculation of a few of the lowesteigenvaluesand corresponding eigenvectorsof large real-symm etricm atrices[J].JCompu t Phys,1975,17:87-94. [6]Cullum JK,W illoughby R A.Lanczos algorithm s for large symm etric eigenvalue computations(I)[M].Boston-Basel-Stuttgart: B irkhauser,1985. [7]Haldane FD M.Spontaneous dim erization in the S=1/2 Heisenberg antiferrom agnetic chainw ith competing interactions[J].PhysRev B,1982,25:4925-4928. [8]EggertS.Num ericalevidence formultip licative logarithm ic corrections from m arginaloperators[J].PhysRev B,1996,54:9612-9615. [9]W h ite SR,A ffleck I.D imerization and incomm ensurate sp iral sp in correlations in the zigzag sp in chain:Analogies to the Kondo lattice [J].PhysRev B,1996,54:9862-9869. [10]Park inson JB.The S=1 quantum sp in chainw ith equalHeisenberg and biquadratic exchange in amagnetic[J].JPhysCondensM att, 1989,(1):6709-6715. M agnetization of 1-d AF Heisenberg System L ISu-yan1,L IYong-m ei2 Them agnetization of1-d AFHeisenberg system was studied using the num ericalDensityM atrix Reno rm alization Group(DMRG)technique.Them agnetization curves at d ifferent frustration were analyzed.In particu lar,them idd le field cusp singu larity appears in them agnetization curveswas described. Density M atrix Reno rm alization Group;Heisenberg system;m agnetization curve;m idd le field cusp singu larity O482.5 A 1672-2590(2010)03-0060-05 2010-04-07 李素艷(1974-),女,山東泰安人,泰山學(xué)院物理與電子工程學(xué)院講師.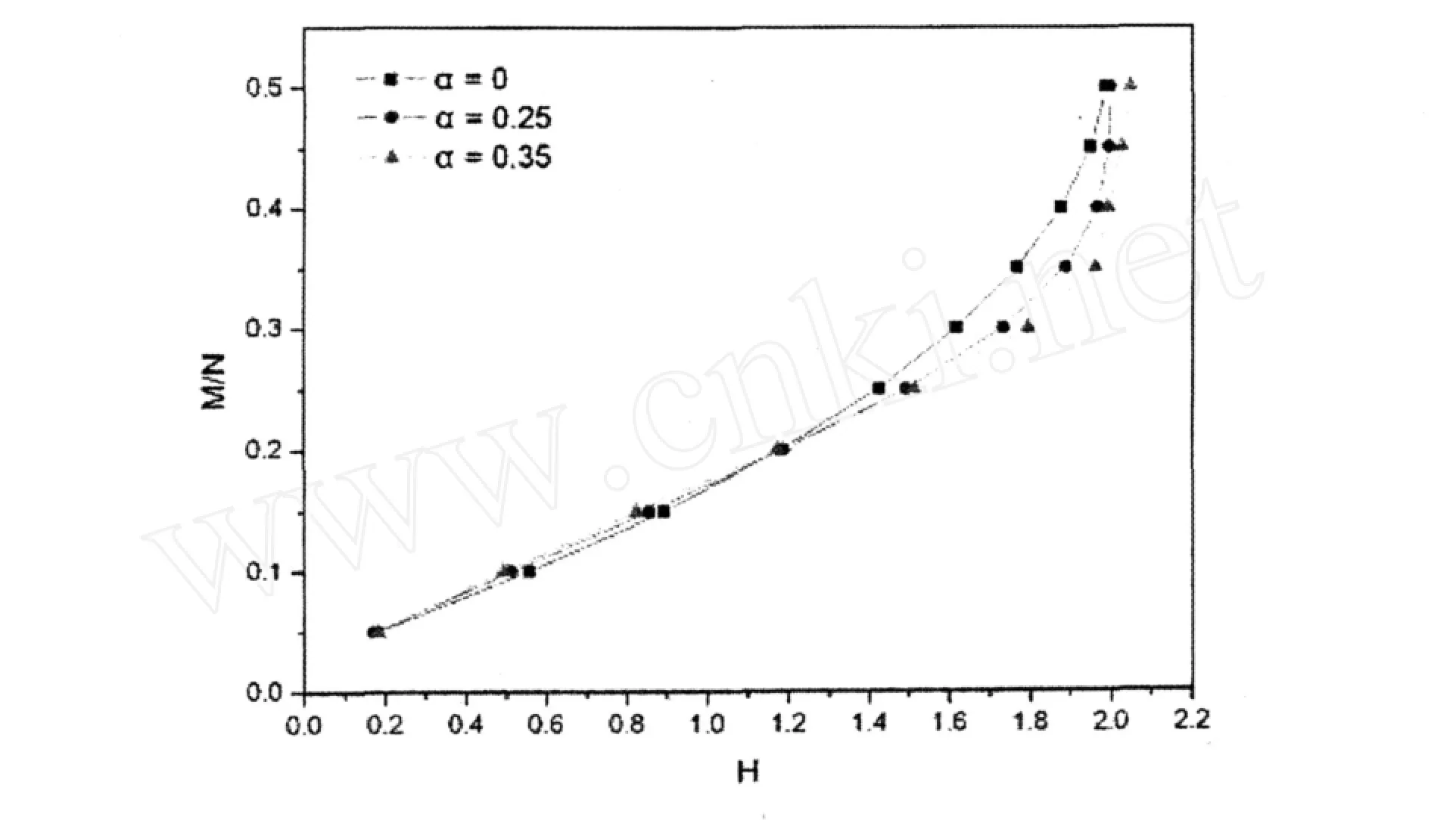
4 小結(jié)
(1.Schoo lof Physicsand E lectronic Engineering,Taishan University,Tai’an,271021;
2.Departm entof Physicsand Info rm ation Engineering,Jining University,Qufu,273155,China)

