Dihu Ouyng , Chunwei Qin , Xiowen Qin *, Qinto Zhng , Xingyu Liu

a Xi'an University of Architecture and Technology, Xi'an 710055, China

b Analysis and Testing Center, Xi'an University of Architecture and Technology, Xi'an 710055, China

c Engineering University of PAP, Xi'an 710086, China

Keywords:KIPs Blunt strike Biomechanical response Damage analysis

ABSTRACT To explore the response law of non-lethal large-size kinetic energy projectiles to blunt attack on skin tissue, and to evaluate the skin injury characteristics of the attacked personnel and the use safety of kinetic energy projectiles.Based on the LS-DYNA simulation software, a three-layer skin simulation model and a Flash-Ball rubber bullet model are established, and the force-time and deformation-time biomechanical corridors of the Flash-Ball rubber bullet impacting human skin tissue are obtained.The corridor curve and the energy transfer and diffusion are analyzed and compared.The safety evaluation of the damage caused by the rubber bullet shooting a human body at different distances is carried out using the empirical formula of the penetration limit.Finally,the safe shooting distance is obtained.The results show that the model used in the simulation has a good correlation with the experimental data, its biomechanical corridor characteristics are different from those of conventional vehicle impact and smallsize projectile response characteristics.The energy transfer and action time of medium and low-speed impact may cause greater damage.The fat layer is the largest energy absorption unit.The minimum safe shooting distance to ensure skin tissue from penetrating damage is 15.8 m, and the limit specific kinetic energy of skin damage is 7.88 J/cm2.This study can be extended to the study of biomechanical response law and safety evaluation under the impact of the same type of large kinetic energy projectile,which provides an important theoretical reference for the police to use large kinetic energy projectiles to conduct safe shooting in peacekeeping operations.

1.Introduction

Because of the convenience of carrying, non-lethal projectile weapons can quickly disperse individuals or people through flash,sound waves, pain, and other strong sensory stimuli, which can improve the effectiveness of disability and ensure the reversibility of personal injuries [1].They have been widely used in antiterrorism, anti-riot, and other social security events.The development of non-lethal weapons has become an important choice to solve local wars [2].The concept of "Non-Lethal Weapons" was formally put forward at the US Non-Lethal Defense Conference in 1996,that is a weapon clearly designed and mainly used to disable personnel and equipment, and to minimize lethal and permanent injuries to people,as well as unintentional damage to property and the environment [3].The explosion pressure wave and its falling and explosive-driven secondary projectiles of explosive projectiles,which are mainly detonated by explosives,may cause serious injury to human tissues[4].It is different from the shock detonation bomb and flash bomb having no difference and a wide range of sensory effects.Kinetic impact projectiles (KIPs) temporarily incapacitate individuals or small groups of people through painful injuries that do not require medical treatment.Police or military combatants can use it in security peacekeeping operations to achieve accurate crowd control [5].With the transformation of modern war form,the riot KIPs have been widely recognized and used by the industry to solve the conflict between non-war personnel, so it is particularly important to adopt more effective weapons for safe operations.There are four common types of anti-riot KIPs in active service,namely hard,rubber,bag,and composite KIPs.For example,AM-40/P, Flash-Ball rubber bullet, ALS 1200 bag bullet, SIR-X, and NS foam rubber/plastic composite bullet [6].The Flash-Ball rubber bullet has a diameter of 44 mm, a mass of 28 g, and maximum kinetic energy of 200 J.However, due to its large size and hollowness, the bullet can avoid piercing the skin to cause pain, Flash-Ball?has been developed in France by Verney and Carron and then widely used in Switzerland and other European countries as a substitute for metal bullets.Unfortunately, since its use, clinical medical cases have been reported one after another, and many scholars have questioned its safety.Navdeep Singh Manhas and others called it“the final weapon before the use of lethal weapons”.Although the Flash-Ball aims to avoid penetrating the skin,the risk of invasive contact damage to subcutaneous soft tissue and viscera cannot be underestimated when the shooting distance is too close and the specific kinetic energy is too large to control [7].Rohini et al.[8] systematically reviewed the literature on deaths and injuries caused by various types of KIPs from 1990 to 2017,including 53 deaths and 300 permanent disabilities.Among 2135 survivors,skin and limb injuries were the most common, and the injuries caused by rubber bullets accounted for 22%of the total number of injuries.Wang [9] cited the typical rubber bullet impact injury cases reported since 2000.Among the 12 cases, half of the Flash-Ball injuries were reported and most of them were contusions and fractures.Peter et al.[10]reported a case of injury caused by a blunt stroke of a Flash-Ball used by Swiss police.An injured person needs to be hospitalized for treatment of cardiopulmonary contusion.Research shows that even if it does not penetrate the skin,its blunt stroke will cause serious damage to internal organs.Therefore, how safe is the Flash-Ball rubber KIPs? How to effectively evaluate its safety? It is a key problem that needs to be solved urgently.

So far,in many foreign Flash-Ball injury cases[11-14],the injury forms are mostly cardiopulmonary contusion and craniocerebral impact.There are few studies on the blocking effect of skin on projectiles.The impact safety assessment of kinetic energy projectiles on the skin is an important field.Skin tissue is the first line of defense to buffer the human body from injury or fatal impact.The energy exchange and quantitative damage assessment of collision systems should be deeply studied.Nevertheless, it is rare to study the impact damage mechanism and energy transfer mode of the widely used large rubber ball, such as the Flash-Ball, on human skin.Tang et al.[15] established a three-layer structure model to simulate the skin,simulated the process of a 4.5 mm shot penetrating the skin using LS-DYNA, and explored the blocking mechanism of the skin on the spherical bullet.

Dimaio et al.[16] conducted skin-blocking experiments by shooting bullets of different calibers into the skin of human lower limbs and obtained the penetration threshold velocities of three kinds of bullets penetrating the skin.Jussila et al.[17] calculated and corrected the penetration threshold velocity of 4.5 mm shot into the skin and verified it through experiments.Breeze and Claser[18] carried out a comprehensive study on the penetration threshold speed of projectiles through the skin,and proposed that"the future skin simulation material model must match the penetration threshold speed".Bao et al.[19] carried out quasi-static tensile and compression experiments on pig muscle, skin and fat,and obtained the mechanical properties parameters of pig skin and fat, and established the corresponding constitutive model.Lu Tianjian et al.[20] studied the relationship between skin tensile deformation and damage after being shot.Papy, A.et al.[21]analyzed the critical specific kinetic energy of skin penetration of small projectiles based on simulated targets.Qin Bin et al.[22]studied the action process of spherical rubber bullets on biological targets and composite simulated targets and proposed that the synergy of the water wave effect and skin stretch effect in the process of blunt impact was the main reason for the skin damage of biological targets.

Bir [23,24] used 18.4 mm caliber rubber bullets to hit the dead body without antiseptic treatment and evaluated the penetration effect of rubber bullets at different speeds on the skin of different parts of the human body.When studying the wounding effects of low-speed bullets on organisms,biological tissues,and pine boards,An Baolin et al.[25]proposed the specific kinetic energy wounding criteria and minimum wounding threshold for different types of bullets and steel balls.

Unlike the high-speed penetration of hard projectiles into the human body, the blunt impact of flexible projectiles on the body and the injury criteria of low penetration is very complex.For people without armor protection, there will be dynamic energy differences due to the impact location, physical fitness, and other conditions, while the injury effects of lethal projectiles are not highly sensitive to these factors.At present,there are many studies on the quantitative analysis (establishment of a mechanical corridor, penetration risk) and qualitative analysis (damage grade,safety distance, and biological injury identification) of the impact load on the targetreceptor.At present, most of the impact studies on the biological thorax and abdomen are based on small highspeed projectiles or rigid rods, while large kinetic energy projectiles are different due to their elastic effects and energy release modes, thus their response characteristics to human injury and safety standards will be very different.Based on LSDYNA numerical simulation and experimental test, Debasis Sahoo et al.[26] predicted the risk of human injury caused by Flash-Ball rubber bullets.The finite element(FE)simulation is verified by force/deformation time data.The correlation value r ＞0.98,the peak force deviation is less than 3%, and the experimental data is consistent with the simulation data.Bracq et al.[27]measured the impact forces of the eXact iMpact?and Flash-Ball? shells based on the numerical simulation of the human chest finite element model HUByx.

The method of reproducing the real impact condition is described.The numerical measurement related to the simulation and pressure field is consistent with the real human body experiment literature.The above research only describes the damage of the Flash-Ball's large-size rubber impact on the head and chest,lacking the finite element model validation of the energy transfer process from the skin surface to the interior, and the model construction of the skin is not refined enough.Therefore, it is particularly important to evaluate the quantitative damage under the impact of large-size rubber bullets in Flash-Ball.

Given the above problems, this paper proposes a three-layer skin structure model to make it close to the real skin injury situation.Taking Flash-Ball rubber bullets as the research object, based on LS-DYNA finite element simulation software, the Flash-Ball rubber elastic model and skin model are verified and checked with experimental data, and the kinetic energy bullet-abdominal biomechanical response corridor is constructed, and its impact response characteristics and energy conversion ratio are analyzed.Based on the calculation and comparison of the error of different empirical formulas for the limited penetration of human skin, the damage risk threshold is obtained, and its safe distance and safe launch speed are determined.This study provides a reference for the analysis of the energy transfer ratio of the skin structure model,the construction of the biomechanical corridor, and the safe operation standard proposed by the combination of the damage criteria,which provides a reference for the study of the damage characteristics of the Flash-Ball large-size rubber bullet on human skin tissue and the future safety design research under the impact of the same type of large-size rubber bullet.It includes the development and research of biological errors and protective equipment of test alternatives, as well as the refinement of new safety evaluation standards for large-caliber rubber bullets, which has important practical significance.

2.Description of the simulation model used for validation

Reasonable assumptions should be made before establishing and verifying the model:

(1) It is assumed that the impact process of the skin substitutebovine skin gelatin composite target used in the literature can replace the impact process of human skin in this paper,and the model parameters are not significantly different from the physical properties of real skin (See the document reference certificate in 3.2 for details).

(2) If the simulation data and experimental error of the rubber bullet (16 mm) impact on the biological target model is acceptable, the calculation accuracy of the model of the Flash-Ball impact on the biological target can be considered acceptable, which ignores the difference of the impactor.

2.1.Description of finite element model of KIPs

According to the experimental device of Debasis Sahooet al.[26]Fig.1 is a simplified schematic diagram of the force wall experimental device developed by the Royal Military Academy (RMA) -Department of Weapon Systems and Ballistics (ABAL) of Belgium.The pneumatic launcher can provide a maximum pressure of 10 bar,and can shoot KIP to a rigid force plate at a specific speed.The ignition solenoid valve allows the compressed air to flow into the rear position through the pipe to launch shells.The launcher is held in a position that stabilizes the aiming point during the test.To ensure orthogonal impact,the barrel and muzzle are placed as close to the rigid wall structure as possible.

This paper uses the Flash-Ball rubber bullet from France as the research object provided by kinetic energy.It is composed of rubber with a diameter of 44 mm and a mass of 28 g.Because this experiment focuses on exploring the deformation of the ball and the force on the force plate during the impact process,it simplifies the rigid wall force wall experimental device and uses LS-DYNA simulation software to create a 3D finite element device grid model, as shown in Fig.2.To avoid different speed measurement positions, the impact speed has a deviation, and at the same time,the calculation resources of the ball flight process are saved.The ball is close enough to the rigid force plate and the ball has a constant initial speed.The full model is adopted for the geometric model.The rigid force column has a diameter of 60 mm, and a length of 40 mm,and a rubber bullet has a diameter of 44 mm,the mapped hexahedron element in Solid 164 eight-node solid element is used for both object models, and the Lagrange gird is used.

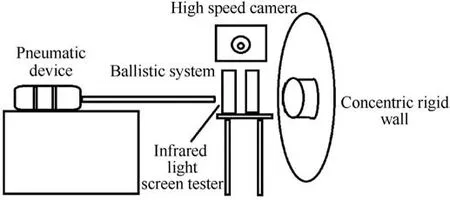
Fig.1.Simplified schematic diagram of force wall experimental device.

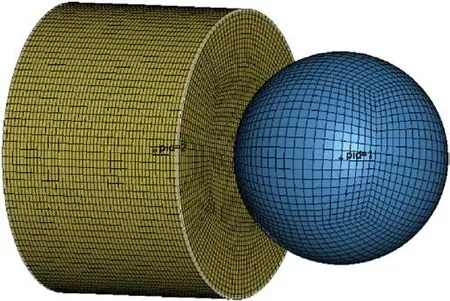
Fig.2.Simplified finite element model of the device.

In solving parameter settings,as Ref.[26]only mentions that the rigid load-bearing wall belongs to steel material,this article intends to use 45# steel with higher hardness as the material of the loadbearing body to ensure the accuracy of the rubber's elastic impact force collected by the rigid load-bearing body.In order to simulate the stress situation of a rigid load-bearing body as accurately as possible, this article compared several material models and finally determined the cylinder adopts *MAT_ PLASTIC_ KINEMATIC material is simulated with a hardening parameter set to 1 to achieve maximum hardness through adjustment and comparison, and displacement constraints in three directions XYZ are applied at the end of the force plate cylinder.After multiple comparisons with experimental data and parameter adjustments,the constraint ratio factor of the soft constraint formula option in the CONTACT_AUTOMATIC_SURFACE_TO_SURFACE keyword was determined to be 0.6 on the surface of the cylinder under force,to avoid abnormal penetration of the contact surface.The rubber bullet body uses *MAT_ HYPERELASTIC_ RUBBER, which is the recommended material model for modeling rubber structures for implicit simulation in LS-DYNA.In this model,the user can specify up to six keywords to directly describe the material behavior.Only C10and C01are defined in this paper,so this model is equivalent to Mooney Rivlin's hyperelastic model.To include the hydrostatic work term WH（J）function of rubber modeling as an unconstrained material in the strain potential energy W, the following Eq.(1)

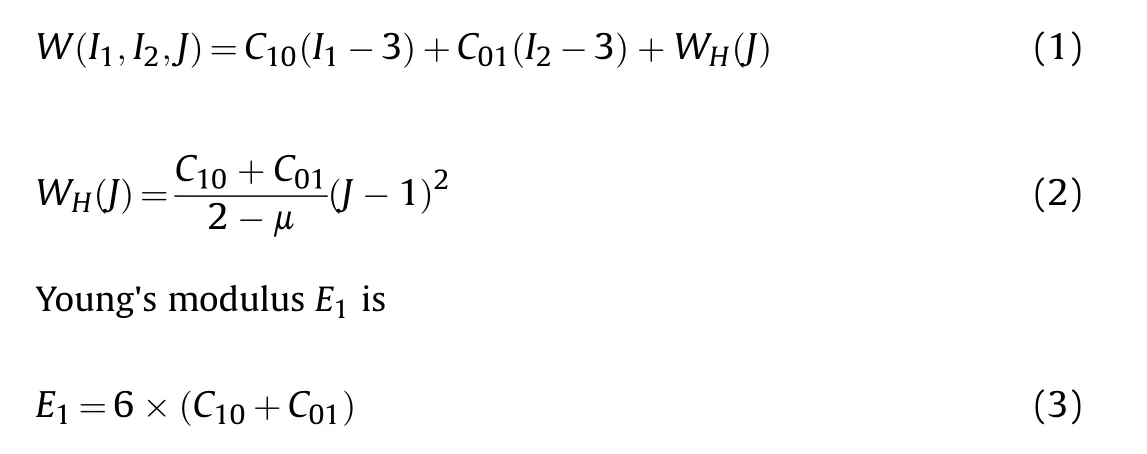
where C10and C01are the material constants determined by experiments; I1and I2are Green tensor invariants; J is the relative volume;μ is Poisson's ratio.

According to the parameter description of rubber materials in the literature[28],the material mechanical properties of the rubber bullet body in this paper are shown in Table 1, the material of the steel bearing plate is 45# steel, and the material mechanical properties are shown in Table 2.

Table 1 Material mechanical properties of Rubber Bullet Body [28].

Table 2 Material mechanical properties of 45# steel[29].

2.2.Description of skin finite element model

In this paper, the skin water wave effect diffusion diameter under the action of stress wave is used as the verification condition of the skin finite element model.The water wave effect and stretching effect are closely related to the mechanism of biological injury.The process of warhead acting on the target includes the superposition of the lateral swelling water wave effect produced by pressurizing the subcutaneous soft tissue and the skin central stretching effect.The synergy of swelling diffusion wave and stretching wave is the cause of skin lesions and pale and red areas of biological injury.The skin stretching speed and scope of action are ahead of the water wave diffusion, and the skin is directly damaged by stretching.The capillaries break due to stretching and form subcutaneous hemorrhage.To explore the cavity and water wave effects caused by blunt impact on biological skin tissues by projectiles,Qin Bin et al.[22] used cowhide and gelatin composite targets to eliminate the complexity and randomness of biological tissues.The non-biological simulation target is composed of cowhide, a fat simulation layer (prepared by boiling with 85%paraffin oil and 15%Kraton resin respectively),and a thick ballistic gelatin with 10% mass fraction, which involves a thickness of 1.5 mm,8 mm,and 15 mm respectively.The gelatin is prepared by mixing 10%gelatin powder and 90%water in a water bath,and it is kept in an incubator at 4°C for 24 h before the test.The size of the gelatin is 300 mm × 300 mm × 150 mm, and the cow leather is pasted on the surface of the gelatin and fixed with elastic ties.

They used a rubber pellet with a hardness of 30°and a diameter of 16 mm to conduct impact tests.The impact response of biological skin is similar to the "fold expansion" of water ripple diffusion rather than simply "stretching inward".The skin transient large deformation water wave effect is a process in which the warhead energy acts on local tissues and rapidly expands to cause progressive damage.There is a complex transformation between the medium kinetic energy and the internal energy of extrusion deformation between the skin and subcutaneous tissues.

For its Ref.[22],the 3D finite element model is established and the gird is divided according to the non-biological simulation target composed of cowhide with a thickness of 1.5 mm, fat simulation layer with a thickness of 8 mm,ballistic gelatin with a thickness of 150 mm,and a rubber bullet with a diameter of 16 mm,the size of the whole non-biological target finite element model is 300 mm × 300 mm × 159.5 mm as shown in Fig.3.The object model grid adopts the mapped hexahedron element in the eightnode solid elements of Solid164,and the Lagrange grid is adopted.

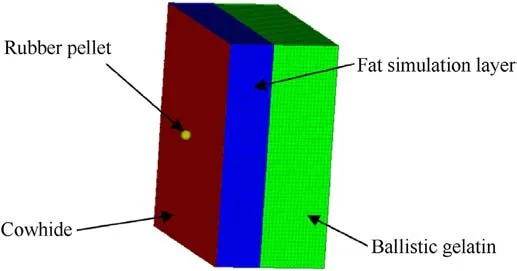
Fig.3.Finite element grid model of biological substitute composite target.

In the parameter setting,the pinball segment contact formula is used, and the constraint scale factor of the option is 0.8.The Mooney Rivlin model is used for the ballistic gelatin material model and the selection of elastoplastic materials for cowhide materials*MAT_PLASTIC_KINEMATIC.The constitutive model of Ogden hyper-elastic material is adopted for fat material, which is a onedimensional quasi-linear, isotropic, and viscoelastic material model close to incompressible.It can represent biological soft tissues such as the brain,kidney,and spleen.Many studies show that the constitutive model of Ogden hyper-elastic material has good nonlinearity compared with other materials at low and medium strain rates.It performs well in the mechanical properties of simulated adipose tissue, and its strain energy density function is shown in Eq.(4):

where λi=1,2,3is 3 main elongation; υ is the shear modulus; α is Ogden coefficient;K is the bulk modulus.The viscoelastic response in this model is expressed as:

where Gijklis the relaxation function.The viscoelastic stress is added to the stress obtained from the strain energy density function.Six terms in the Prony series indicate that the relaxation function is introduced into the strain rate function,and its equation is:

where Giis the shear modulus;βiis the attenuation constant.Specific parameters are shown in Tables 3-5 [30-32].

2.3.Grid convergence test

Due to the impact experiment simulation of rubber bullets and skin targets as a system in this article,it is necessary to achieve grid convergence on the basis of unifying the grid division size of rubber bullets and skin targets as much as possible.Therefore,this article intends to evaluate the independence of the grid by changing the grid size of two impact physical models based on literature experimental data, and by plotting the variation curves of the r correlation coefficient between simulated calculation values and experimental results under different grid densities, to find the convergence interval of the r value to evaluate the grid independence, and to determine an accurate grid partitioning method so that the correlation coefficient r does not change with the decrease of the grid.

To quantify the verification process between the simulation prediction and the experimental data, Pearson Correlation Coefficient is introduced to measure whether the two data sets are on the same line.It can be used to measure the linear relationship between distance variables.The calculation formula is

where r is the Pearson correlation coefficient, xiand yiare the ithdata corresponding to two data sets, and N is the total number of data.The range of correlation value r is 0.1-0.3 indicating poor correlation, while 0.5-1 indicates a strong correlation between curves.

In this chapter,we plan to set the grid sizes of the rubber elastic diameter D(mm)and the skin target length L(mm)for 1/8,1/16,1/32,1/64,1/128,1/256,respectively(D=44 mm,L=300 mm).We will divide the physical models of the two experimental systems described in sections 2.1 and 2.2 into grids.By comparing the correlation coefficient r between the rubber elastic deformation and the force value of the rigid plate under the impact speed of 56.2 m/s in the rigid wall experiment conducted by Debasis Sahoo et al.[26],we will explore the convergence range of the rubber elastic grid.In the experiment in Ref.[22], the correlation coefficient r of the diffusion diameter time-history curve was measured to explore the grid convergence interval of the skin target.The variation curve of the correlation value r between the simulation results and the literature experiments is shown in Fig.4.From the figure, we can see that when the grid size of the rubber elastic reaches 1/64, the correlation values r of the rubber elastic deformation and stress value of the rigid plate reach 0.92 and 0.94,respectively.Moreover,with the decrease in grid density, the correlation value r does not continue to increase.Therefore, it can be considered that the division of grid size has met the convergence requirements.Similarly,the correlation value r of the diffusion diameter of the skin water wave effect converged when the grid size of the skin target model reaches 1/128 L.Therefore, to ensure that the grid size of the impactor and receptor is consistent as much as possible, the grid size of the rubber ball and skin target is controlled between 0.6 and 0.7 mm.

3.Comparative analysis of grid convergence testing and simulation validation results

3.1.Verification of finite element model of the KIPs

In this paper,the process of impacting the rigid stressed plate is used to obtain the stress and rubber elastic deformation of thestressed plate, which is compared with the force wall experiment results in the literature [22], and the rubber elastic finite element model is checked.

Table 3 Material mechanical properties of Ballistic Gelatin Material.

Table 4 Material mechanical properties of Skin.

Table 5 Material mechanical properties of Fat Simulation Materials.

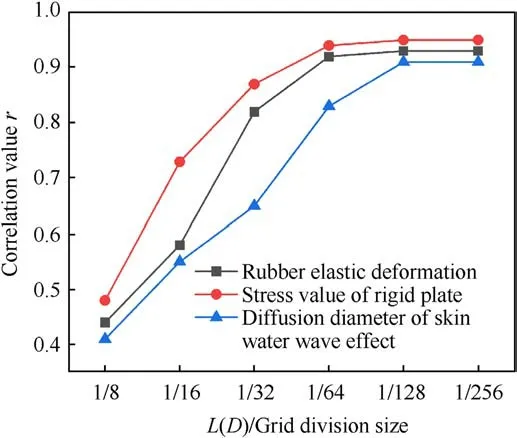
Fig.4.Change curve of model calculation values and experimental correlation values r under different grid sizes.

Based on the rigid force wall experiment of Debasis Sahoo[26],the three average velocities representing the low, medium, and high-speed ranges(low-speed range 51.8-62.5 m/s,medium speed range 71.5-79.2 m/s, and high-speed range 92.9-122.2 m/s),namely 56.2 m/s, 73.9 m/s, and 109.2 m/s, are used as the initial velocities of the rubber ball to impact the rigid force plate,using lsdyna_smp_d_ R11_1_0_Win64 solver.In five simulation periods,the comparison between the experimental deformation image in literature with an average impact velocity of 56.2 m/s and the numerical simulation is shown in Fig.5.

It can be seen from Fig.5 that the difference between the numerical simulation and experimental deformation results is small when the rubber's elasticityis continuously compressed to the maximum deformation, and the front rebound of the numerical rubber's elasticity lags behind the experiment when rebounding back.The force-time relationship of the rigid plate between the simulation data in this paper and the experimental data in the literature under three average speeds is plotted respectively, and the results are shown in Fig.6.The average deformation time diagram of the rubber elastic extracted from the simulation results and the average experimental deformation data at three average speeds representing three-speed ranges are plotted in Fig.7.From the force-time curve (Fig.6) and deformation time curve (Fig.7) after the impact within 1.5 ms,it can be seen that with the increase of the average impact speed,the force bearing time of the rigid force plate is shrinking and the peak force is increasing.With the increase of the average impact speed, the deformation rebound period of the rubber's elasticity spring is shrinking,which is more obvious in the simulation, but the peak deformation of the rubber's elasticity spring almost all fluctuates around 30 mm, and the deformation rebound speed in the simulation is faster than that in the experiment.

The calculated results are summarized in Fig.8 concerning the peak deviation percentage of the rubber's elastic deformation and the correlation value r of the deformation and the stress value of the rigid plate at three average speeds representing three-speed ranges.In the 3 bar charts of Fig.8, green represents the deformation of the rubber's elasticity, and orange represents the stress value of the rigid plate.It can be seen from Figs.8(a)and 8(c)that the average deviation of the peak value of rubber's elastic deformation and stress value of rigid plate are less than 5%, and the correlation value r is greater than 0.5 which involves a good correlation.It can be seen from Fig.8(b)that the peak value of the force on the rigid plate in the simulation calculation is greater than the experimental measurement results at three average speeds, and the time to reach the peak value is earlier than the experiment from the low-speed and medium-speed,and lags behind the experiment from the high-speed impact, the correlation value r is higher than 0.8, which has a strong correlation with the experimental measurement value in the literature.The simulation data error is acceptable.

3.2.Verification of skin finite element model

In the simulation of the experiment process of a rubber bullet impacting cowhide gelatin biomimetic target with a diameter of 16 mm, the water wave effect diffusion diameter of skin tissue is simplified as the horizontal distance of the circular water ripple peak in the model's front view, which is recorded as D (mm), as shown in Fig.9.The time history curve of the diffusion diameter measured in the literature [22] experiment and the simulated diffusion diameter change curve calculated at three speeds are plotted in Fig.10.After calculation at the impact velocity of 153.9 m/s, the simulated correlation values r of diffusion diameter of the skin water wave effect were 0.995, 0.997, and 0.998, respectively.With the increase of impact velocity of rubber bullets, the correlation value r of diffusion diameter gradually increased, and the r values at three speeds were greater than 0.5 showing a strong correlation.

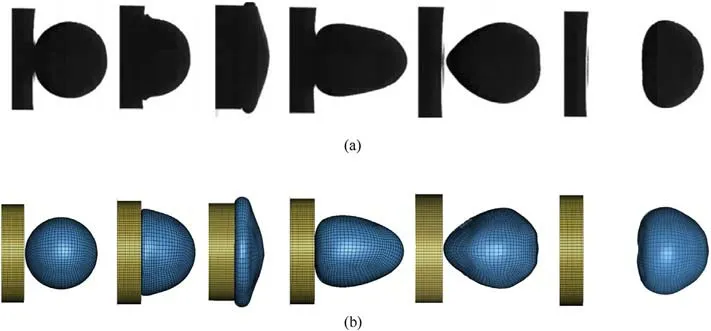
Fig.5.Rubber elastic deformation in the experiment and simulation of literature [26] at an average impact velocity of 56.2 m/s: (a) Literature experiment results; (b) Simulation results in this paper.

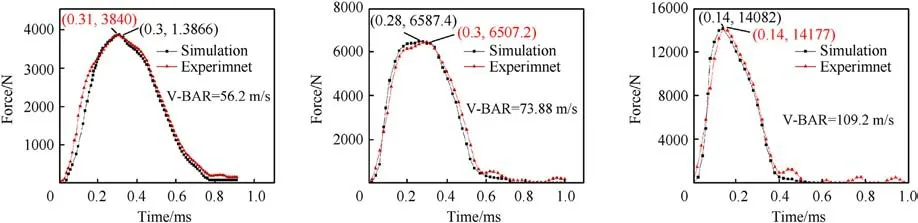
Fig.6.Time history curves of rigid plate force between simulation data and literature experimental data at three average speeds.

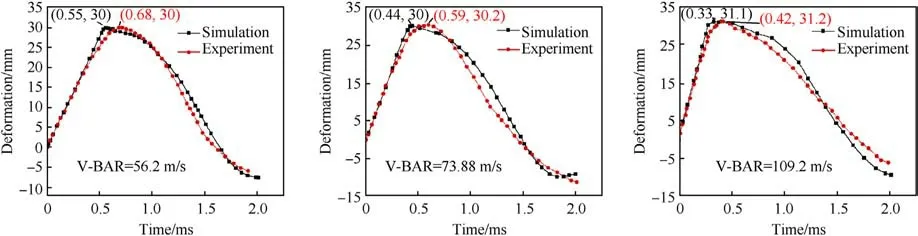
Fig.7.Time history curves of rubber elastic deformation of simulation data and literature experimental data at three average speeds.

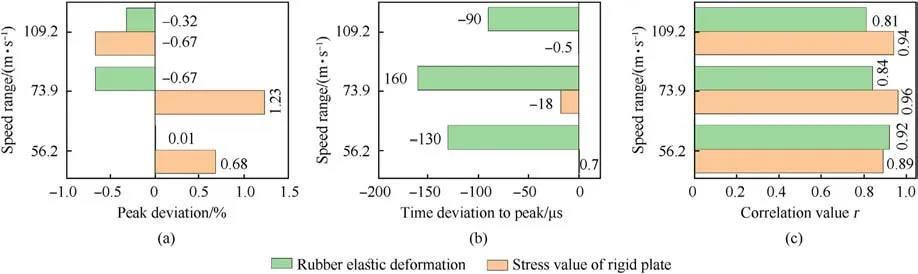
Fig.8.Peak error: (a) peak interval time error; (b) correlation value r bar chart of quality experience; (c) simulation under different average speeds.

Qin Bin [22] explained why simulated biological targets were used instead of real biological tissues: it was to eliminate the randomness of biological tissues, such as age and physical condition, the fear of living organisms, and the inability to carefully observe the trajectory and profile deformation, but it did not explain how well biological substitutes fit with real biological tissues.In this paper,by comparing the water wave effect diameter of the skin finite element model with the biological substitute composite target experiment in the literature,it is verified that the skin model establishment and parameter settings in this paper are highly consistent with the physical properties of the biological substitute.Many scholars have proved that Kraton resin (fat simulation layer) and ballistic gelatin (the substitute of subcutaneous tissue layer in the literature experiment)are similar to human adipose muscle tissue because of their similar density,viscoelasticity, good homogeneity, and transparency [33,34].It is widely used as a soft tissue simulator in biomedicine and terminal trajectory [35-37].Jiang Mingfei [38], Mogulin [39] and others carried out gelatin dynamic mechanical property tests and applied them to the numerical simulation of killing element penetrating gelatin target, proving that it can better represent the physical effects produced by killing element penetrating human tissues.Jussila et al.[40,41]found that the mechanical properties of cow skin and adult male skin were relatively close when they researched the target material of simulated skin.Xiong et al.[42,43]compared the mechanical properties, limited penetration properties, and impact damage characteristics of human skin and cow skin to quantitatively evaluate the similarity between cow skin and human skin.The results show that the simulated skin has a similar ballistic limit to the skin of the typical part of the human body, and shows a"water wave effect" similar to the biological skin.AEP-94 in NATO document STANREC 4744 [44] clearly states that the internal composition of the substitute used to evaluate the occurrence of penetration consists of ballistic gelatin with a mass fraction of 20%.

Fig.9.Diameter measurement of water wave effect diffusion effect of 16 mm rubber bullet used as a simulation target.

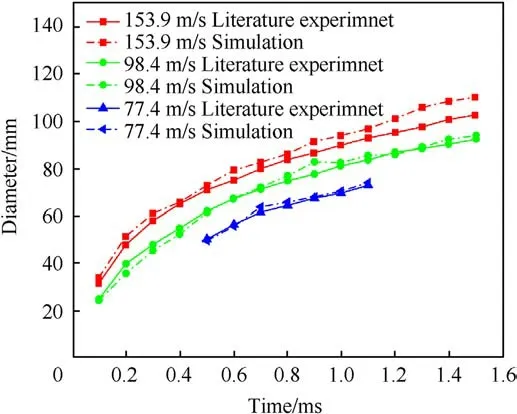
Fig.10.Diffusion diameter change curve of skin water wave effect in literature experiment and simulation.

In a word, the combination of these three materials has a high degree of agreement with the physical and mechanical properties of human skin tissue, so this paper can think that the skin finite element model established in this paper can be used to simulate and calculate the force on the real human skin.

4.Simulation and damage analysis of blunt biological target

4.1.Description of the simulation model of rubber bullet blunt impact on the biological target

After the above tests on the finite element model of the Flash-Ball rubber elastic and the bionic skin model, the data obtained from the impact experiment process reproduced by the constitutive model,material parameters,and grid parameter models of the rubber bullet and skin used in the simulation of this paper have reached the ideal correlation value with the experimental literature data.In this paper,referring to the general anatomical structure of human skin under normal conditions, the finite element model of skin tissue is simplified into three layers, namely, the epidermis,dermis,and subcutaneous tissue layer.The thickness of the dermis determines the skin thickness.Collagen fibers are the main reason why the dermis can withstand large stress and deformation [45].Xu Renchao et al.[46]used high-frequency ultrasound to detect the thickness of the skin epidermis and dermis in multiple parts of the body of healthy adults.The results showed that the thickness of the skin epidermis and dermis of Han healthy adults was 0.2028 ± 0.02925 mm, and the thickness of the dermis was 1.5819 ± 0.31710 mm.The thickness of subcutaneous tissue of normal healthy adults is about 5-15 mm, and the thickness of subcutaneous fat is about 30-40 mm.Based on the safety principle,the thickness is the minimum.The skin surface area is tentatively determined as 0.3 m×0.3 m,the thickness of the upper epidermis is 0.17 mm,the thickness of the dermis is 1.5 mm,the thickness of subcutaneous tissue is taken as 5 mm,and the thickness of adipose tissue is taken as 30 mm,so the total thickness below the dermis is 35 mm.The rubber elastic model material and model parameters are the same as those in Section 2.1.The object model grid adopts the mapped hexahedron element in the eight-node solid elements of Solid164, and the Lagrange grid is adopted.According to the determination of grid size in Section 2.3,the grid size of the rubber bullet and skin target is controlled between 0.6 and 0.7 mm.As the skin thickness is only 0.17 mm, the thickness of its grid cells is adjusted to 0.085 mm,which is a two-layer grid with a length and width of 0.6 mm.The total number of grids is about 1000000.Its 3D finite element model is shown in Fig.11.To prevent displacement of the skin model, only vertical and bottom direction displacement constraints are set at the bottom of the model.Due to the significant difference in hardness between the upper surface of the skin model and the rubber elastic contact,it is easy to cause abnormal contact penetration of the grid.Therefore,the constraint ratio factor of the soft constraint formula option in CONTACT_AUTOMATIC_SURFACE_TOSURFACE is also set to 0.85 to avoid abnormal penetration of the contact surface.

The skin layer model adopts the elastoplastic model *MAT_PLASTIC_ KINEMATIC keyword definition, Mooney Rivlin model is adopted for dermis model, *MAT_ HYPERELASTIC_ RUBBER keyword definition, subcutaneous tissue and fat model adopt Ogden model, *MAT_ QUASILINEAR_ VISCOELASTIC keyword definition, model material parameters are the same as Tables 3-5 in Section 2.2.Concerning the initial speed of rubber bullets, according to the energy standard and injury criterion table of anti-riot kinetic energy projectile against the human body specified in National Military Use Standard of the People's Republic of China -GJBZ20262-95 Anti-riot Kinetic Energy Bomb Power Standard.

It is specified that the specific kinetic energy of kinetic energy projectile in contact with skin will cause moderate damage (III) at 12-30 J/cm2,slight damage(II)at 4-12 J/cm2,and slight damage(I)at 0.5-4.0 J/cm2,so the three specific kinetic energy thresholds are calculated.The three velocity thresholds are 23 m/s, 66 m/s, and 114 m/s.In this paper, three initial velocities are applied to the rubber elastic model to analyze the stress deformation of the skin and the energy transfer between the shell skin.The calculation time is 5 ms.

4.2.Analysis of simulation results of rubber bullet blunt impact on the biological target

After LS-DYNA calculation, we take the speed of 66 m/s as an example to evaluate the skin response after impact, and the von Mises stress cloud diagram of the quarter section of the skin during the impact process is shown in Fig.12.

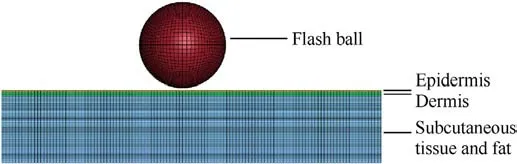
Fig.11.Rubber elastic three-layer skin finite element model.

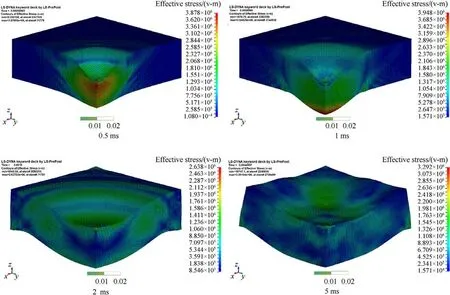
Fig.12.von Mises Stress Cloud Chart of Skin under Impact within 5 ms.

Fig.13.Velocity vector nephogram of skin model unit under extrusion and tension.

It can be seen from the von Mises stress diagram that,within the impact time of 0-0.5 ms, the rubber elastic continued to move downward, and the impacted area continued to sag.The stress concentration value at the contact center directly in front of the skin model and the rubber elastic was the largest.From the axial view of the profile,the stress was concentrated in the middle layer,that is,the upper part of the subcutaneous tissue,and there was no obvious bulge at the lower end of the skin model.The stress wave propagates downward within 0.5-1 ms, and the stress is concentrated at the lower end of subcutaneous fat.The skin bulge diameter is about 45 mm.With the expansion and development of the plastic deformation of the skin model, the stress concentration of the skin model gradually weakens, and the peak stress decreases.The 1-2 ms internal stress wave releases and diffuses from the fat layer to the surrounding areas, and the stress wave develops and propagates upward in a wavy form.The skin bulge diameter is about 95 mm.Within 2-5 ms, the bullet body stops rebounding and starts to rebound upward.When the stress wave reaches the edge of the model,it spreads to the center of the skin surface.The skin model finally tends to be stable after two times of stress wave center convergence.

At the initial stage of the impact of the rubber bullet, the skin water wave effect is obvious, which can be divided into the combined action of the compression movement of the transverse water wave effect and the longitudinal skin stretching.Fig.13 is the velocity vector cloud diagram of the force-bearing unit of the skin model.It can be seen from Fig.13 that Vais the velocity vector generated by the transverse compression of the water wave effect,and Vbis the velocity vector generated by the longitudinal skin stretching.A stress wave is the propagation form of stress and strain disturbance.In a deformable solid medium, the mechanical disturbance is represented by the change of particle velocity and the corresponding change of stress and strain state.The change of stress and strain state propagates in the form of a wave.With the help of the interpretation of stress wave theory, the diffusion degree of the water wave effect is mainly related to the shear modulus of the wave propagation medium.It can be seen from the cloud chart that the wavefront is circular.The outward diffusion speed of the shear wave of the water wave effect is fast in the early stage of the shock.The disturbance wave speed attenuates rapidly due to the damping effect in the process of transverse propagation, and the attenuation speed is faster than the longitudinal tensile velocity vector.

When the speed reaches 114 m/s, the skin is damaged, the epidermis and dermis are torn and peeled off,and the bottom of the fat layer is concave and peeled off due to the impact, as shown in Fig.14,so the force and deformation response under the impact of 114 m/s speed impact will not be considered below.To explore the impact velocity threshold of skin damage,the initial velocity of the Flash-Ball rubber bullet is given in the speed range of 66-114 m/s.As shown in Table 6, it is roughly found that the rubber bullet penetrates the skin to cause damage,and the velocity threshold for penetrating the internal tissue is 92.5 m/s (see Fig.15).

Fig.14.Fracture state of skin model unit under the impact at the speed of 114 m/s.

Table 6 State performance of skin tissue model under different impact speeds.

Take six uniformly distributed element nodes along the diameter of the largest circular area of the skin depression, and output the node force by defining the node group to obtain the node force and NCFORCE file.This file can be customized to output the node number,output the node force Resultant-force in ASCII,and output the force and displacement time history curve of its element.For the skin force and deformation curves at different impact speeds,take the average of the force or deformation loading values at each time point of the six units measured, and calculate the standard deviation.The upper bound of the corridor is the average value plus a standard deviation, and the lower bound is the average value minus a standard deviation.The upper and lower bounds are piecewise linear fitted so that the piecewise continuous linear approximation curves of the upper and lower bounds of each corridor are qualitatively established.Through the upper and lower boundaries of the corridor that can closely contain data, the slope and intercept values with slight separation deviation can be obtained, and the obvious force and deformation trend of global geometry can be intuitively reflected by the force and deformation curve of the unit group with slightly larger fluctuations.

It can be seen from the corridor curve of skin stress change at impact speeds of 114 m/s, 66 m/s, and 23 m/s that Fig.15 can be regarded as the time history change characterized by peak force and platform response.The force curve rises sharply at first,drops immediately after reaching the peak value, then a force-bearing platform lasts for a while, and then drops slowly to zero, and the total force-bearing time is about 1.1 ms.Under medium-speed impact, the range of peak force is about half of that under highspeed impact.The curve first reaches a force-bearing platform,and the average impact duration is roughly the same as that under high-speed impact.After reaching the peak, it immediately drops slowly to zero,and the total force bearing time is roughly the same as that under high-speed impact.Under low-speed impact, the curve trend is consistent with that of medium-speed impact.The peak force range of skin force,the minimum time to reach the peak force,the average impact duration,and the total force duration are summarized in Table 7.

It can be seen from the deformation corridor curve of skin tissue(Fig.16) that with the increase in impact speed, the deformation time curve presents a plateau trend.Under high-speed impact,the average compression ratio is 15.4%-44.1%.Due to the elastic rebound of the skin, the deformation curve first reaches the peak value of deformation, and after it recovers to zero deformation, it sagged again.The peak value of secondary sagging deformation is twice that of the first and then tends to be stable.The peak deformation is the upper platform, and the deformation is restored to the lower platform.Under medium-speed impact, the peak deformation of the second sag is larger than that of the first, with an average compression of 2.4%-37.8%.Under low-speed impact, the curve shows only one platform, with an average compression of 4.3%-12.7%.The response time characteristics of skin tissue deformation are shown in Table 8.

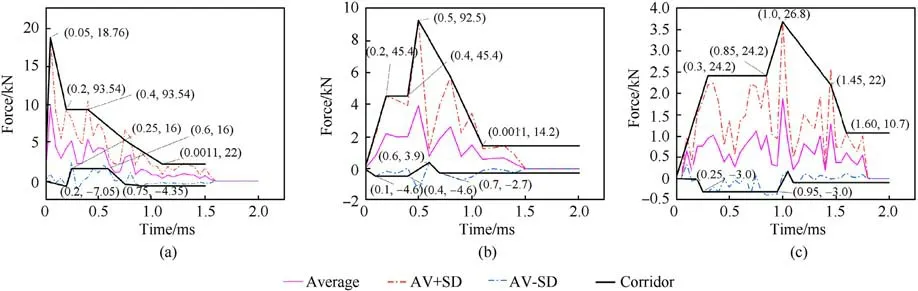
Fig.15.Corridor Curve of Skin Stress at Different Speeds: (a) 114 m/s force-time; (b) 66 m/s force-time; (c) 23 m/s force-time.

Table 7 Stress response time characteristics of skin tissue at different impact speeds.

Fig.16.Corridor Curves of Skin Deformation Time Course at Different Speeds: (a) 114 m/s deformation-time; (b) 66 m/s deformation-time; (c) 23 m/s deformation-time.

Table 8 Response time characteristics of skin tissue deformation at different impact speeds.

From the above analysis,it can be seen that with the increase in impact speed,the stress platform will lag behind the time when the peak stress occurs.The increased multiple peak force is consistent with that of impact velocity.The minimum time to reach the peak force is shortened.The force platform value is about half of the peak force, the duration of the force platform is shortened, and the duration of the force platform is unchanged when it develops to high-speed impact.The total stress time is shortened,and the time is unchanged when it develops to high-speed impact.The deformation time of skin tissue is longer than that of force, showing a double platform trend under medium-speed and high-speed impact.Under high-speed impact, the time required for the skin unit to reach the peak deformation is later than the time to reach the peak force,while under the low-speed impact,the time will be earlier.The total action time of the force is generally consistent with the end time of the first deformation.With the increase of impact speed, the time to reach the maximum deformation and the duration of deformation double platforms both increase first and then decrease, owing to the compression deformation time of the rubber bullet under high-speed and low-speed impact which is smaller than that under medium-speed impact.The peak value of secondary compression under medium velocity impact is larger than that of the first,and the total deformation time is roughly the same.

Compared with David C.Viano [47] and Warren N.Hardy et al.[48]rigid bar hitting the abdomen,the total force-bearing time and the duration of the force-bearing platform are shorter.Different from the trend of the force-bearing curve of Cynthia Bir et al.[24] 140g KIPs impacting the chest at a speed of 20-60 m/s, the force-time curve of the simulation experiment in this paper is composed of the instantaneous peak stress and the force-bearing platform, and the duration of the force bearing is longer than the chest.Platform and peak trend distribution are related to speed.The deformation curve shows a double platform trend within 5 ms rather than a slow increase and tends to be stable.Kroell et al.[49] conducted a lowspeed abdominal impact experiment on the interior of a car (23 kg rigid body impacted at a speed of 4.4-9.5 m/s).The peak force was 3300-6500 N, the compression ratio was 18.5%-41.8%, and the impact duration was 40-60 m/s.Compared with the automobile safety experiment, the impact simulation of a large-sized rubber bullet on the abdomen in this paper had a larger peak force, a smaller difference in compression ratio,and a shorter duration.

Fig.17 shows the curve of the energy change of the rubber bullet at different impact speeds.At the initial speeds of 114 m/s,66 m/s,and 23 m/s,the initial energy of the rubber bullet is 375.6 J,125.9 J,and 15.6 J.Combined with the local enlargement diagram under the impact at 23 m/s in Fig.17, it can be seen that the time when the energy is transmitted to the skin and does not drop is 0.55 ms,0.60 ms,and 0.90 ms,respectively.Then contact the skin to make it rise from the lowest initial energy to the stable rebound kinetic energy in the rebound process in 0.7 ms, 0.9 ms, and 1.8 ms,respectively, and the average kinetic energy is 22.5 J, 12.8 J, and 2.9 J.It can be seen from the rubber elastic energy change curve that with the increase of impact speed,the time required for the rubber elastic energy transmission to bounce back after contact with the bullet body is shortened,and the time for the skin to absorb energy is reduced.Suppose that part of the kinetic energy of the rubber bullet is converted into its strain energy, and the other part of the energy transmitted to each layer of skin is completely converted into the internal energy of the skin.Ignoring the influence of gravity in a short distance, the velocity of the bullet when it contacts the skin does not attenuate, which is the initial velocity.The energy absorption percentage of each layer of skin tissue and the energy transmission percentage of the rubber bullet at the three speeds are obtained from Eq.(8), which are summarized in Fig.18.

where EAis the percentage of energy absorption, %; ETis the percentage of energy transmission,%; EKis the contact energy of the rubber bullet, J; ERis the rebound energy of the rubber bullet, J;EImaxis the maximum internal energy of skin tissue, J.

Fig.17.Curve of rubber elastic energy change at different impact speeds.

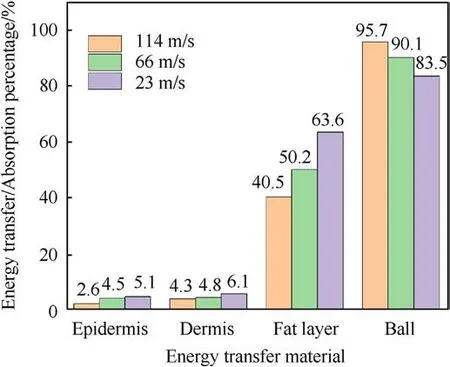
Fig.18.Percentage of material energy released/absorbed at three different speeds.

The maximum internal energy change curve of each part is derived from the HISTORY option of LS-DYNA software, and the maximum internal energy is summarized in Fig.18.It can be seen from Fig.17 that the maximum energy transmission ratio of rubber bullets is 95.7%, and the energy transmission ratio increases with the increase of impact speed.At the same impact speed,the energy absorption rate of the fat layer was the highest(63.6%)followed by the dermis,and the epidermis was the lowest,with the increase of impact velocity, the energy absorption percentage of each layer of skin tissue decreased.From the above analysis of energy change,it can be seen that under the high-speed impact, the contact time between the projectile and the skin surface decreases, the energy transmission ratio of the projectile increases,the energy absorption percentage of the skin tissue decreases, and fat tissue is the main carrier of energy absorption.According to the analysis of energy transfer and stress deformation of skin tissue, the arrival time of peak stress and the arrival time of maximum deformation is different,which indicates that the skin damage caused by large KIPs is similar to the simulation results of Wang song et al.[50]involving the impact of rubber bullet on the chest.The difference is that under the medium and high-speed impact, the compression and rebound degree of the projectile is large,but the peak stress can be reached within a short contact time.After a large amount of energy transfer, the skin tissue will continue to compress until it reaches the maximum deformation.Under the low-speed impact, the compression rebound degree of the projectile is small,but after the contact reaches the maximum deformation, the energy transfer process is long,and the peak force occurs in the rebound process of the projectile.That is, the degree of damage is not limited to the impact time,but lies in the time course of energy transmission and diffusion between the projectile and skin tissue.

From the above conclusion, it is not difficult to see that under the same initial kinetic energy,the smaller the spherical projectile density is, the greater the energy dissipation ratio of the larger projectile body may be, and the more obvious the skin-blocking effect is.In the protection of personnel in the far field, it is not enough to consider the stress of the skin under the impact of the projectile and reduce the deformation value.In the case of medium and low-speed impact, the energy absorption and diffusion of the protective equipment should be considered.In future research,the stiffness of protective equipment should be focused on under highspeed impact,and the energy absorption and diffusion of protective equipment should be focused on under medium and low-speed impact.

5.Shooting safety evaluation with skin penetration as a risk

Compared with other human tissues(such as viscera,bone,etc.),skin is less vulnerable to ballistic damage of large-size warheads.It may tear, but because of the subcutaneous tissue buffer, there is usually very little damaged skin that needs to be removed.To determine the threshold speed required to penetrate human skin,a large number of studies have been carried out.Some researchers have removed the skin from human cadavers and conducted isolation tests on them.Vogel[51] conducted an extensive in vitro study involving 348 autopsy samples.Samples were taken from the skin above the sternum.Cut dumbbell specimens along the same axis.The sample is 50 mm long and 4 mm wide in a narrow section.At the age of 30, the skin thickness is about 1.75 mm, the tensile strength is 20 MPa,and the elongation at break is 72%.There is little difference between the skin thickness and strength and the set value of the simulation parameters in this paper.As stated in Section 4, the importance of skin as a part of the energy absorption system is because the skin sample alone is subject to impact,which depends on the transverse or longitudinal tensile fracture of the skin itself without considering the impact of the extrusion or tensile stress of the tissue under the skin.Therefore, based on the multi-layer structure of the skin, this paper expects to obtain the threshold of safe shooting distance without penetrating the skin.

Based on the results of previous PMHS ballistic tests, some researchers infer that skin penetration is related to the cross-section density of the projectile body and put forward four empirical formulas for limiting penetration velocity as shown below [40,52].According to the literature [53,54] empirical formula #1 is as follows:

where vthis the maximum penetration velocity of the warhead,S is the warhead cross-section density, S=m/Se , m is the warhead mass, and Se is the warhead cross-section area.

According to Ref.[55], empirical formula #2 is as follows:

Table 9 Comparison between the calculated results of the skin model and the results of empirical equations with different ultimate penetration velocities.

where e is the specific kinetic energy of the projectile,J/cm2;E is the kinetic energy of the projectile, J; A is the impact cross-sectional area of the projectile, cm2.If the projectile is impacted straightly,the cross-sectional area can be calculated as a circular area;m is the mass of the projectile, kg; v is the projectile impact velocity, m/s;d is the diameter of the projectile, cm.This standard applies to projectile materials with a Shore hardness of less than 90.Nsiampa et al.[58]obtained the velocity attenuation equation of projectile in flight through fitting in the experimental analysis of chest injury as follows:

where Vxis the projectile velocity after the attenuation after x m,m/s; V0is the initial velocity of the projectile, m/s; d is the projectile diameter, m; ρ is the air density, kg/m3, and the air density ρ is 1.29 kg/m3;CD0is the air resistance coefficient.Since the windward area of the rubber elastic can be approximately treated as a spherical structure, CD0is taken as 0.5; m is the mass of the projectile, kg.In this paper, the safe distance range is calculated according to Eqs.(14)and(15).The kinetic energy of the French Flash-Ball rubber bullet can reach up to 200 J,and it can be calculated that the initial velocity V0can reach up to about 120 m/s.According to the threshold value of skin damage impact velocity obtained in section 4.2, the specific kinetic energy of skin damage limit in the simulation calculation is 7.88 J/cm2calculated according to Eq.(13).The comparison results of the empirical equations of different limit penetration velocities of human skin are shown in Table 9.By comparing the different empirical formulas with the results of the simulation test in this paper,it can be concluded that the empirical formula#2 derived by J.Sperazza et al.has a good prediction effect on the skin penetration speed threshold of Flash-Ball.Compared with other formulas, the deviation value from the simulation experiment is the smallest which is 5.3%.We can know that the reliability of the simulation results is acceptable.So far,according to the simulation results and Eqs.(13-15),this paper can conclude that the theoretical penetration limit distance of Flash-Ball is 15.8 m,that is when the shooting distance of Flash-Ball to the human body is less than 15.8 m,there will be a risk of penetrating the skin and invading the deep tissues of the human body, causing damage to the muscular and viscera.

6.Conclusions

In this paper,three layers of human skin tissue were established by LS-DYNA simulation.The simulation experiment was carried out on the Flash-Ball large-size rubber bullet to replace the skin tissue target under the high,medium,and low-speed respectively.Based on the experimental data, the model verification of the rubber bullet and skin tissue was carried out, and the biomechanical corridor was established for its force-time response curve and deformation-time response curve at different speeds, and the change of energy transfer was analyzed,Finally,the safety distance and safety speed standard of the Flash-Ball large-size rubber bullet are evaluated based on the empirical formula,and the conclusions are as follows:

(1) In comparison with the impact test data,the maximum error between the deformation peak value and the deformation arrival time is less than 5%, and the minimum correlation value r is greater than 0.5.The simulation results have a strong correlation with the experimental results.

(2) In this paper, the force-time curve of the simulation experiment is composed of instantaneous peak stress and the stress platform, the sustained stress time is long, and the platform and peak trend distribution are related to the velocity,the deformation curve shows a double-platform trend within 5 ms.

(3) There are differences in the time between the peak stress and the peak deformation of the skin hit by the large-size projectile.The water wave effect also exists when large rubber bullets impact the skin,and the energy release ratio of rubber bullets gradually increases with the increase of speed, and the energy absorption rate of fat is the largest.The increase in impact speed may not increase the effect of injury to a certain extent.Under the condition of not penetrating the skin, the large kinetic energy projectile has a long energy transmission process under the medium-speed impact,which may cause greater damage to the skin tissue.

(4) Through the comparison of four groups of skin penetration empirical formulas, the Flash-Ball rubber bullets are within 15.8 m of the close range, and the specific kinetic energy of skin damage limit in the simulation calculation is 7.88 J/cm2.When shooting at the human body, the use of indirect shooting should be prohibited,to avoid skin penetration and invasion causing damage to the internal tissues of the human body.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.