Li Bing , Yting Gu , Lnke Hu , Li Bowen , Yng Lihu , Jue Wng , Yue Yin ,*

a Northwestern Polytechnical University, Xi'an 710072, China

b China Academy of Information and Communications Technology, Beijing 100191, China

c China Intelligent and Connected Vehicles (Beijing) Research Institute Co., Ltd, Beijing 100176, China

d The 20th Research Institute of China Electronic Technology Group Corporation, Xi’an 710068, China

e Xidian University, Xi'an 710071, China

Keywords:Satellite network Deep space communications Internet of military things Non-orthogonal multiple access MIMO Link-16 JITDS

ABSTRACT One of the major challenges arising in internet of military things (IoMT) is accommodating massive connectivity while providing guaranteed quality of service(QoS)in terms of ultra-high reliability.In this regard,this paper presents a class of code-domain nonorthogonal multiple accesses(NOMAs) for uplink ultra reliable networking of massive IoMT based on tactical datalink such as Link-16 and joint tactical information distribution system(JTIDS).In the considered scenario,a satellite equipped with Nr antennas servers K devices including vehicles, drones, ships, sensors, handset radios, etc.Nonorthogonal coded modulation,a special form of multiple input multiple output(MIMO)-NOMA is proposed.The discussion starts with evaluating the output signal to interference-plus-noise(SINR)of receiver filter,leading to the unveiling of a closed-form expression for overloading systems as the number of users is significantly larger than the number of devices admitted such that massive connectivity is rendered.The expression allows for the development of simple yet successful interference suppression based on power allocation and phase shaping techniques that maximizes the sum rate since it is equivalent to fixed-point programming as can be proved.The proposed design is exemplified by nonlinear modulation schemes such as minimum shift keying (MSK) and Gaussian MSK (GMSK), two pivotal modulation formats in IoMT standards such as Link-16 and JITDS.Numerical results show that near capacity performance is offered.Fortunately, the performance is obtained using simple forward error corrections (FECs) of higher coding rate than existing schemes do, while the transmit power is reduced by 6 dB.The proposed design finds wide applications not only in IoMT but also in deep space communications, where ultra reliability and massive connectivity is a keen concern.

1.Introduction

The development of fifth generation(5G)and beyond gives birth to Internet of things(IoT)which manages to establish connections among massive devices.As a special case of IoT [1,2], Internet of military things (IoMT) emerged as a promising candidate for warfare,not only due to the capability of enabling multiple access over a single resource block but also enabling ubiquitous awareness of battlefield situations [3-5].To this end, one of the key enabler is non-orthogonal multiple access (NOMA), a recently developed technique for sharing radio resources among concurrent units including vehicles, drones, ships, sensors, handset radios, etc.

1.1.Previous work

With the proliferation of multiple input multiple output(MIMO)technique in integrated networking as demonstrated in, e.g.Refs.[6,7],the combination of MIMO and NOMA,i.e.,MIMO-NOMA,emerges as a new enabler offering greener,faster and more reliable communications among IoMT devices.Different from conventional multiuser MIMO, MIMO-NOMA seeks to offer improved spectral efficiency for overloaded MIMO, i.e., an AP equipped with Nrantennas serves K concurrent users given K/Nr＞1 [8].Powerdomain NOMA (P-NOMA) was first adopted to construct MIMONOMAs as illustrated in Ref.[9] with main focus on downlink multi-cluster transmission, where each cluster accommodates several users presuming they experience channels of strong correlation but of significantly different path loss.These users share an identical beamformer.In this setup, clusters are simply interference-free and users within each cluster are distinguished using power control, a scenario that P-NOMA is capable of.In general,MIMO-NOMA in power domain can find wide applications in 5G and beyond[10].

As an alternative approach, code-domain NOMA (C-NOMA) is able to offer capacity approaching performance in overloaded MIMO-NOMA as well as demonstrated in Refs.[11-13].In Ref.[11],a graph-based detector is proposed to reduce the detection complexity while offering maximum-likelihood detection like performance.In Ref.[12], low-density parity check (LDPC) codes based on rate allocation technique is proposed.It is shown, near capacity performance is obtained as the code length N approaches infinity.Similar results are also presented in Ref.[13] where construction of high rate turbo-like codes are attempted to offer improved sum rate successfully.

While P-NOMA and C-NOMA types MIMO-NOMA both offer massive connectivity as well as ultra-high reliability in terms of very low bit error rate (BER).These two types are drastically different.The most apparent difference between C-NOMA and PNOMA is perhaps the former is more concerned with practical coded modulation schemes while the latter is more signal to interference-plus-noise (SINR) centric.As a result of this subtle difference, C-NOMA based MIMO-NOMA does not necessarily rely on optimized beamformers to mitigate severe multiuser interference but favors forward error corrections (FECs) instead.

1.2.Motivations and contributions

Though MIMO-NOMA is considered well established in civilian networks,the application in military networks especially IoMT has gained attention very recently.Existing military networks employ orthogonal multiple access such as time division multiple access(TDMA) in Link-16 [14].TDMA renders low complexity access control but insures long latency due to queuing for the next round of transmission.Alternatively, NOMA permits random and simultaneous access [15], which is appealing in IoMT scenarios with a large number of military equipment.In Ref.[16], P-NOMA-aided integrated network is considered.It is demonstrated that NOMA outperforms OMA significantly in terms of connectivity and data rate.The improvement is further strengthened if MIMO beamforming is utilized[17].Unfortunately,the design and performance analysis presumes Gaussian codebook.

Though non-Gaussian codebook schemes are considered in CNOMA such as Refs.[11-13],most existing MIMO-NOMAs focus on linear modulation such as phase shift keying (PSK) while leaving nonlinear modulation such as continuous phase modulation(CPM)unaddressed.Hence two prominent IoMT standards Link-16 and joint tactical information distribution system[14]cannot enjoy the improved spectral efficiency and massive connectivity as existing NOMAs do, since binary CPMs: minimum shift keying (MSK) and Gaussian MSK (GMSK) are adopted for energy efficiency transmission to avoid nonlinear distortion due to high power amplifier.The feasibility of CPM-based NOMA was initiated in Ref.[18] and then Refs.[19-22], which confirms that CPM offers significantly improved spectral efficiency.But the discussion so far has been dedicated to small scale networks.

In this regard, the construction of CPM based code domain MIMO-NOMA is attempted in this paper, with special focuses on uplink transmission.The contributions of the paper are listed below.

(1) High overloading.Though overloading is a routine superiority of NOMA over OMA, the proposed scheme nonorthogoanl coded modulation (NCM) further strengths this feature by easily accommodating K ＞30 single-antenna users with only a few receiver antennas Nr≤8.Fortunately,NCM does not resort to very low rate FEC for such high user load.The code rate R ≥1/3 and the resultant normalized overloading is as high as Ω=KR/Nr?1,which is hardly approached in existing C-NOMA schemes, where R ＜1/10 is frequently required for the same user load K, see Ref.[23] and the references therein.

(2) Simple power allocation.Thanks to the asymptotical performance analysis based on η-transform [24], closed-form expression for SINR is obtained.The expression decouples receiver filter and power allocation,and hence allows for simple recursive power allocation scheme termed ideal power allocation(IPA)relying only on channel state information(CSI)H.It is further proved that IPA is equivalent to iterative fixed-point programming and hence maximizes the sum rate.Further discussion reveals that network fairness is also offered by IPA leveraging the result in Ref.[25].

(3) Versatility and low complexity.As a C-NOMA, only simple convolutional code(CC)and repetition code(REP)are considered to keep the transceiver complexity as low as possible.This strategy is by no means optimal, but still offers near capacity performance with varying blocklength N, user load K and number of receiver antenna Nr.A comparison with existing results unveils that NCM offers comparable or even better performance in terms of bit error rate(BER)in heavily overloaded setups without requiring case-bybase design as advocated in Ref.[15].

As a result, NCM enables massive connectivity and ultra reliability simultaneously.Moreover, the power allocation algorithm IPA does not require iterative optimization, which is widely adopted in existing schemes, see Ref.[26] and references therein.The rest of the paper is organized as follows.Section 2 presents the NCM system model;Section 3 presents the design and performance analysis based on η-transform, which leads to the development of IPA; Section 4 presents the numerical results and discussion; Section 5 concludes the paper.

2.MIMO-NOMA: Nonorthogonal coded modulation

In Fig.1(a), the typical IoMT scenario is demonstrated, where a satellite is used to collect data from massive devices such as warships,tanks,helicopters and so on.This paper focuses on the uplink transmission over block Rayleigh fading channels, the equivalent parameterized model is presented in Fig.1(b),where an access point(AP) of Nrantennas serves K single-antenna users indexed by K : = [1, 2, …, K].The CSI matrix H =[h1,h2,…,hk,…,hK] collects the CSI vector hk∈Kexperienced by the k-th user.It is assumed constant within each transmission of frame and the columns hkare ordered according to the Frobenius norm‖h1‖2F≥‖h2‖2F≥…≥‖hK‖2Fwithout loss of generality.The elements hik,?i=1,2,…,Nrare independent and i.i.d normal random variables,i.e.hik～CN （0,1）are known to AP and user k.The user k expects to transmit at rate Rkgiven power pkand the total transmission power pT= ∑k∈Kpk.Since devices in IoMT are mainly sensors, handsets, weapons, human-wearable devices and smart munitions, which are equipped with single-antenna,the discussion in sequel is dedicated to single-antenna users.But the derivations can be easily generalized to handle multi-antenna users.

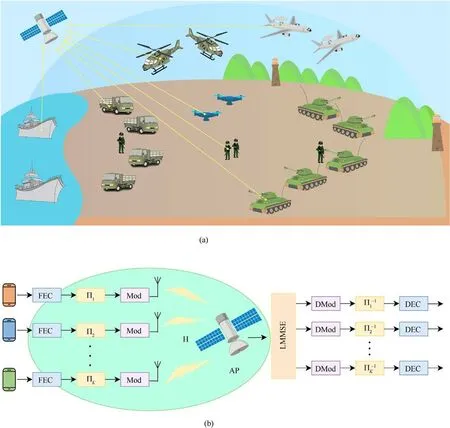
Fig.1.IoMT scenario and equivalent system model: (a) IoMT Based on tactical datalink; (b) Uplink transmission of NCM.

2.1.Introduction to NCM transceiver

From the perspective of coded modulation theory [13], NCM is nothing but an application of serially concatenated coded modulation in multiuser communications.Without loss of generality,NCM is exemplified using the k-th user.

where pkis the transmission power,θkis a user-specific phase offset and T is the symbol duration.

The information-bearing phase ψ（t,ckn） admits a titled-phase writes [27,28].

and for GMSK(L = 2):

where Bbis set to BbT =0.5 and Q（·） stands for the Gaussian Qfunction [27].

where hk=[hik]Nr×1is the CSI vector of user-k and ζ（t） is additive white Gaussian noise(AWGN).Using orthogonal decomposition of CPM based on principal component analysis (PCA) [29], the underlying CPM signal admits the following discrete expression:

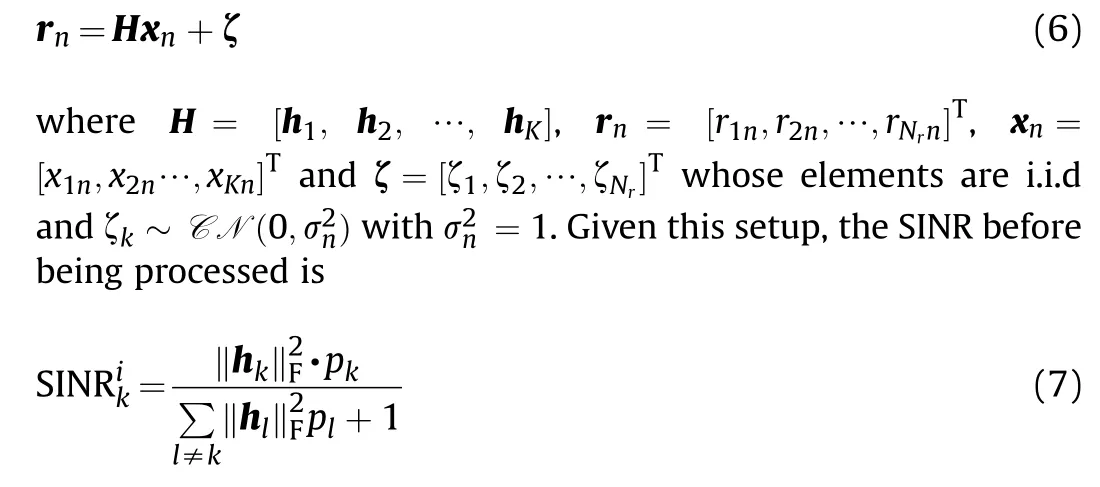
which is extremely low as K→∞.To enhance SINR,linear minimum mean squared error (LMMSE) filter is applied to rnto produce an interference suppressed signal snreads Ref.[30].

Based on Gaussian approximation, ρknis interpreted as an AWGN that is independent of ?skn, whose mean and variance are respectively expressed as [30]

which indicates clearly that near single user performance is obtained if the interference is perfectly cancelled.This observation necessaries the joint decoding-demodulation process presented in sequel, where CPM demodulator (DMod) and FEC decoder (DEC)are two a posteriori probability (APP) decoders that exchange extrinsic information iteratively attempting to get reliable decision of information sequence bk.

The DMod block (i.e., the inner decoder) accepts sn=[s1n,s2n,…,sKn]Tand the a priori log-likelihood ratios (LLRs)Liac =[Liac（k,n）]K×Nregarding ckand outputs the extrinsic LLRs L iec =[Liec（k,n）]K×Nand L iex =[Liex（k,n,m）]K×N×Mregarding ckand xk, respectively [28,31].The extrinsic information Lie（k,n）generated reads

where xkis a collection of interfering signals.The expression consists of three terms.The first term is interpreted as the single user detection metric scaled by SINR and the second term is AWGN noise.The first two terms are supposed to deliver exactly the same decision identical to single user system (since the only the sign matters for decision making) if without the presence of the third term ?k, a random variable collecting the residual interference.Since Lis（k,n,i）is Gaussian distributed,it is rational to assume that ?kis Gaussian distributed as well, whose mean E（?k）= 0 and variance Var（?k）≠0.?kis termed as the effective interference and the minimization of Var（?k） will be addressed latter.

The calculated Liecis then fed to DEC to obtain the priori information Liaregarding ckfor the next round iteration.After imaxiterations, Liexis fed to LMMSE to calculate W, which is updated once for each user to keep the complexity as low as possible,though it can be updated each iteration.

3.η-Transform aided design and performance analysis

This section attempts to provide a unified solution for design and performance analysis of overloaded MIMO-NOMA based on CPM where Nr,K ?1 while β =K/Nr＞1.Hence η-transform from random matrix theory is exploited to establish a deterministic equivalence,a approach proved to offer accurate enough results as illustrated in Refs.[24,32].Without loss of generality,the discussion is focused on the k-th user equipped with single-antenna but the results can be generalized to deal with multi-antenna users in principle as presented in Ref.[24].

3.1.Problem formulation

For binary CPM based MIMO-NOMA,the achievable information rate Rkis expressed as [27,28,33]

where B accounts for the normalized power-in-band bandwidth of CPM, which is 0.6 and 0.5 for MSK and GMSK [27], respectively.Hence the performance analysis becomes SINR centric and the design of MIMO-NOMA is primarily focused on the maximizing sum rate problem, reads

where ?k,l∈K,Rsumis the sum rate,p=[p1,p2,…,pK]is a possible power allocation scheme and γthis the minimum required SINRokto enable Rkaccording to Eq.(19), where all Rk,?k∈K are assumed equal.Unfortunately,both the object and the constraint in Eq.(20)are non-convex in general.Hence iterative programming methods such as iterative fixed-point programming is employed to find a feasible solution [34].This paper attempts to address Eq.(20)alternatively from the perspective of random matrix theory, since the entire system becomes deterministic as K,Nr?1 while β keeps invariant, which is exactly a large scale overloaded MU-MIMO of great interest.The toolset employed is η-transform [24] and the definition is presented below.

Definition 1.The η-transform of a nonnegative random variable X is defined as:

where γ is a nonnegative real number and ηX（γ）∈（0,1].ηX（γ） is closely related to Stielejes transform SX（·） as:

For convenience,a collection of lemmas regarding S -transform and η-transform is presented in Appendix A, which is frequently referred to.

3.2.η-Transform aided SINR analysis

The first step is to calculate SINRokand then examine the asymptotical behavior.To this end, the power of the signal in Eq.(10), after some manipulations according to Eqs.(11) and (12), is rewritten as

3.3.Closed-form power allocation

Assuming perfect removal of interfering signals from stronger users indexed by l ＜k Eq.(26) now reads

Recalling the original problem Eq.(20),it is wondered if IPA is a feasible solution.First it is easy to check the constraints are automatically satisfied by replacing Eq.(20b) with Eq.(17).But is IPA optimal enough to maximize the sum rate Rsum.As a matter of fact,IPA is optimal in the sense that it is a feasible solution of the problem Eq.(20) and the reasoning is detailed below.

Lemma 2.IPA maximizes sum rate Rsumsince it offers a feasible solution to the following fixed-point equation:

Proof.See Appendix C.

The conclusion can be even strengthened seeing the fact that iterative fixed-point is equivalent to fractional programming and weighted MMSE (WMMSE) as already proved in Ref.[34].But different from these algorithms, IPA does not resort to iterative search, which is an appealing property in practice especially in IoMT scenarios.Another concern is about the fairness of IPA,since each user is allocated different power.It is straightforward to prove that IPA achieves network level fairness～(as sketched in Appendix D.

Though similar power allocation is used in Refs.[13,35], where the geometric ratio is obtained through extensive trial and optimization.In this paper, a closed-form is obtained and is further shown to be equivalent to iterative fixed point algorithm, which was not known before.

3.4.Phase shaping technique

So far the discussion is SINR centric implying the coded modulation is Gaussian distributed to guarantee the promised performance, which can be challenging as practical coded modulation schemes are employed [8].Now in this subsection, the impact of CPM waveform is evaluated.Following up the result in Eq.(18),where the second part ?kcollects the interference and hence is identified as the effective interference.Since ?kis assumed Gaussian random variable and E（?k） =0,the focus is thus Var（?k）.

To simplify the design, linear phase spacing is adopted in Eq.(18) [18-22],

Based on this model it is demonstrated that Var（?k） is minimized when θΔ=π/2.The claim is formalized below:

Lemma 3.Var（?k） is expressed as:

where δkis a constant determined by power allocation p and θΔwhich is minimized when θΔ=π/2.

Proof.Please see Appendix E.

As detailed in the proof of Lemma 3, the role of phase shaping technique in terms of θΔis an effective measure to suppress the interference by reducing the correlation among signals from different users.Such measure was widely adopted in C-NOMA as early as in code division multiple access (CDMA), where long spreading sequence is appealed for minimizing correlation among users[36].However,this operation leads to very low code rate and bandwidth expansion inevitably, which is even worse if FECs present.Fortunately, it appears that a simple phase rotation θΔoffers the same function without sacrificing performance.Such configuration was also used in code domain MIMO-NOMA, see Ref.[37],where each user is assigned a unique θk,i.e.,θΔ=2π/K.However,such measure may not be necessarily optimal at least in CPM based NOMA, as calculated.

3.5.NCM vs.MIMO-OMA

Since NCM is a special case of MIMO-NOMA which outperforms MIMO-OMA in general, NCM can thus offer improved spectral efficiency [2].However, it is still desirable to confirm such claim taking the proposed IPA into consideration.

Based on the above discussion,the sum rate of NCM Rsumis reexpressed as

where the last line is obtained using Lemma3 [2].In contrast the sum rate of MIMO-OMA, R′sumis upper-bounded as

It is thus seen that NCM outperforms MIMO-OMA in terms of sum rate.

So far, the design and performance analysis regarding power allocation and waveform optimization have been studied extensively.Though the design is exemplified using single-antenna users,the method can be easily used to tack multi-antenna users as illustrated in Ref.[24].Further, the obtained performance can be interpreted as a baseline since multi-antenna users reap more energy efficiency in general.

3.6.Implementation

3.6.1.Determining γth

As can be seen that γthplays a crucial role.There are two major methods in determining γthin general.In P-NOMA such as Ref.[9],γthis essentially the Shannon limit.In C-NOMA,γthis the convergence threshold one way or another.This method is adopted as well in this paper.It turns out that γth≈10 log10（2Rk/B-1）+1 dB,where Rk=R log2J with J = 2 for both MSK and GMSK [38].The determined γthis presented in Table 1, where γ*this obtained assuming Gaussian signaling.As expected, NCM requires higher transmit power than Gaussian signaling does.

3.6.2.Large scale fading

So far the discussion has dedicated to Rayleigh fading without taking large scale fading into consideration.Though it was point out in Refs.[24,32]results hold valid as large scale fading presents,it is necessary to address this concern briefly.

The CSI matrix with the presence of large scale fading now reads Refs.[9,10].

it is readily seen that MIMO-NOMA with large scale fading is no different from MIMO-NOMA considering only small scale fading except for the attenuation factor dk.Hence the proceeding discussion can be applied seamlessly and the obtained power allocation is identical, apart from a factor D1/2.

Further, it is predicted that the proposed deterministic equivalence can be generalized to joint design of beamforming and power allocation of large scale MIMO-NOMA.The verification remains a future topic.

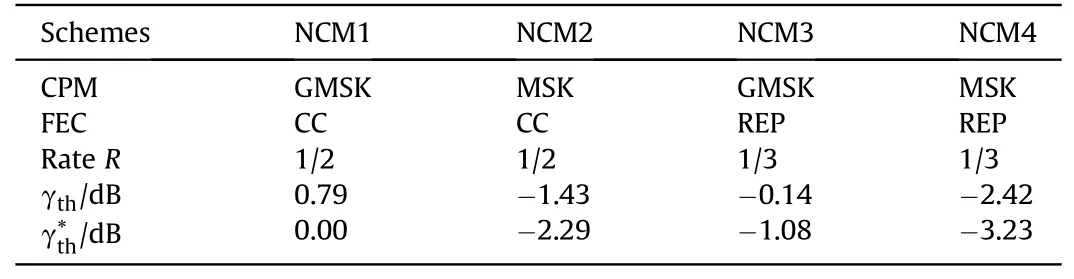
Table 1 γth of different NCMs.

3.6.3.Code rate R

It is assumed that each user employs an identical FEC of rate R.NCM picks up two simple representative FECs: CC and REP, where the former is convolutional with R=1/2 and the latter is linear with R=1/3.REP with R=1/2 is out of consideration since it generates weight-2 error events that is catastrophic [38].It is observed that the code rate in either case is much higher than existing schemes,where very low rate (R?0.1) FECs with optimized configurations[13,15]are preferred to support tens of users.Hence NCM is nothing special from existing NOMAs in supporting high user load (as confirmed in Section 5), but can offer low latency transmission in the sense that NCM attempts much less transmissions.

3.6.4.Complexity

As can be seen, the complexity is one of the most concerned issues throughout the design of NCM.The FECs employed, namely 2-state CC(2,3)8and linear block code REP,are among the simplest schemes,where the decoding complexity is negligible in contrast to existing schemes where powerful yet complex FECs are used and hundreds of iterations are needed [39].As a matter of fact, the complexity of NCM mainly comes from the LMMSE filter, where matrix inversion is required to calculate W.The complexity is determined as O （imaxN3r）, which should be acceptable for Nr＜10.Further, to speed up the calculations an optimized library is used[40].

4.Numerical results

This section presents the numerical performance evaluation of the NCM.In the simulated systems, AP is equipped with Nrantennas while all K users are all single-antenna.The channel experiences block fading as mentioned earlier.Four different configurations of in terms of FEC and CPM are considered.The decoder and demodulator are configured to iterate imax= 15.The scheme from Ref.[39]is presented as a benchmark.Just like NCM,the benchmark scheme has Nr=8,K = 32 and binary PSK (BPSK).But the code rate R = 1/10, which inevitably leads low sum rate Rsum= 3.2.The details are presented in Table 2.The overloading factor Ω=KR/Nris presented as a unified indicator of the overloading capability of NOMAs of different Nr,K and R.The purpose of this section is to show that NCM can support not only a large number of K users, but also very high sum rate Rsum, which is a challenging task for existing schemes.

4.1.Increasing user load K

The discussion starts with evaluating the performance of NCM as the user load K increases.Four configurations from Table 2 are considered.The parameters are N=8192,Nr=8 and K=16,24.The results are presented in Fig.2.It is observed that in all cases,NCM can approach the capacity and gap is around 6 dB disregarding the user load K The interesting part is that when targeting the same Rsumsuch as 8.00 bit/s/Hz for NCM1 and NCM3, and 6.67 bit/s/Hz for NCM2 and NCM4,REP coded systems reduce transmit power by approximately 2 dB even it requires 1.5-times user load than CCbased systems do.It appears that lower rate renders low transmit power.However,this observation needs further study.For example,optimized CC of rate 1/2 is not considered and it is hence not appropriate to claim that low rate is superior at this moment.

4.2.Finite blocklength vs.infinite blocklength

Now NCMs are evaluated in both finite blocklength regime and infinite blocklength regime with N increases from 512 to 32768.The results are presented in Figs.3 and 4.

First NCMs given N = 512 are considered in Fig.3.The systems are all configured with Nr=8 and the focus is to reveal the interplay between user load K and Eb/N0.As can be seen, to attain BER=10-4or lower the required Eb/N0increases as K increases.It is perceived that the performance degrades significantly comparing with the NCMs with N presented in Fig.2.Taking NCM1 for example,the gap is approximately 1 dB when K=16 and increases to approximately 8 dB when K=32.Similar behaviors appear in the rest of the systems.The reason is mainly due to the reduction of interleaving gain as the block length is shortened.Hence it is expected that increasing N alleviates the performance degradation.Such expectation is confirmed in Fig.4.

As observed in Fig.4,the sum rates are achievable as N increases from 2048 to 32768, significant improvement is offered.For example, the improvements are approximately 3 dB when CC and REP are employed, respectively.This improvement is due to interleaving gain [13,38], a valuable property inherited from serially concatenated coded modulation.It is also observed that the gaps to the channel capacities are approximately 8 dB and 5.5 dB, respectively.These significant gaps are mainly due to the block fading setup that intends to put the entire frame into deep-fading, especially when Eb/N0is low.Similar phenomena appear not only in NCM but also in existing code-domain MIMO-NOMA,see Ref.[39],where the gap to channel capacity is merely 1 dB presuming hkvaries each symbol interval but degrades by 0.45 dB when hkvaries every 400 symbols and N = 40960.If the scheme in Ref.[39] is configured to experience the same block fading, the results are detailed in the following subsection.

4.3.Timeliness

Timeliness is one of the major concerns in integrated network.In Fig.5, the timeliness of the proposed NCM is evaluated using stochastic network calculus(SNC)[41],where the probability pd（w）that the delay violates the maximum allowable delay w is evaluated.The parameter w is measured in slot.For a given w, delay exceeds w if xd, i.e, the amount of data per user fed to network,exceeds the data-offloading capability of the network.Further a parameter θ is introduced to fine-tune and minimize pd（w）.In the context of IoMT, xdis modeled as a Poisson random variable with parameter Nain bits and the data-offloading capability isdetermined by SINRok.For more details,please see Refs.[41,42]and the references therein.

Table 2 The Configurations of NCMs.

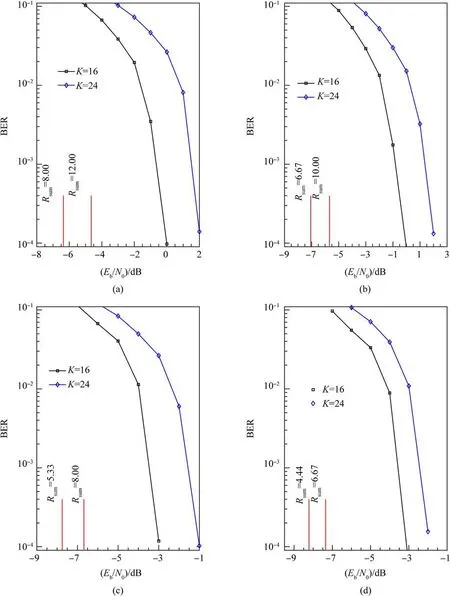
Fig.2.The performance of four NCM configurations shown in Table 2.Nr=8,N=8192 in all cases.The vertical lines indicate the corresponding capacities:(a)NCM1;(b)NCM2;(c)NCM3; (d) NCM4.

Fig.3.The performance of four NCM configurations with varying user load K shown in Table 2 Nr =8,N =512 in all cases: (a) NCM1; (b) NCM2; (c) NCM3; (d) NCM4.

First in Fig.5(a), the timeliness is exemplified using NCM1 by evaluating pd（w）vs.θ given Na=256 bits.It is shown that pd（w）is reduced from approximately 10-1to 10-10by tuning θ and increasing w from 1 to 7.From the results,it can be concluded that almost loss-free (＜10-5) delivery can be guaranteed by setting w = 5.Unfortunately, instantaneous delivery is not guaranteed as pd（w）≈10-1by setting w=1.Fortunately,by reducing Nafrom 256 to 64, successful and instantaneous transmission is attained as demonstrated in Fig.5(b).This figure presents the interplay between pd（w） and code rate R However, w needs to increase as R reduces to make sure pd（w）≈10-5can be approached.Such behavior appears since low rate NCM1 attempts more transmission than high rate NCM1 does given the same size of data chunk, and inevitably experiences high probability of delay violation.It is worth noticing that such behavior roots in low code rate R, which suggests that high code rate should be employed for timeliness.Similar observation irrespective of the coded modulation scheme is also presented in Ref.[15]

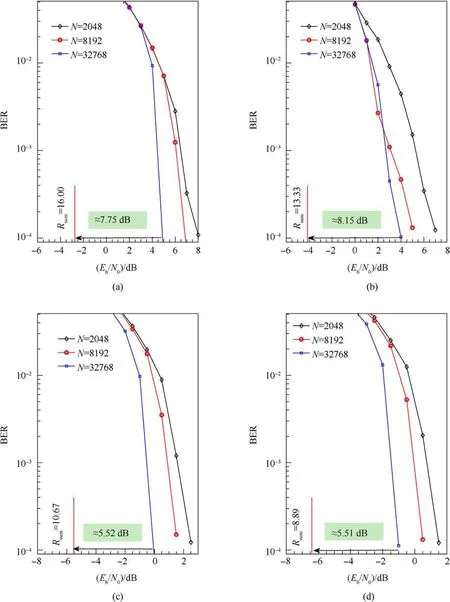
Fig.4.The performance of four NCM configurations shown in Table 2.Nr =8,K =32 in all cases.The vertical lines indicate the corresponding capacities: (a) NCM1 with Rsum = 16.00 bits/s/Hz; (b) NCM2 with Rsum = 13.33 bits/s/Hz; (c) NCM1 with Rsum = 110.67 bits/s/Hz; (d) NCM1 with Rsum = 8.89 bits/s/Hz.

4.4.Comparison with benchmark systems

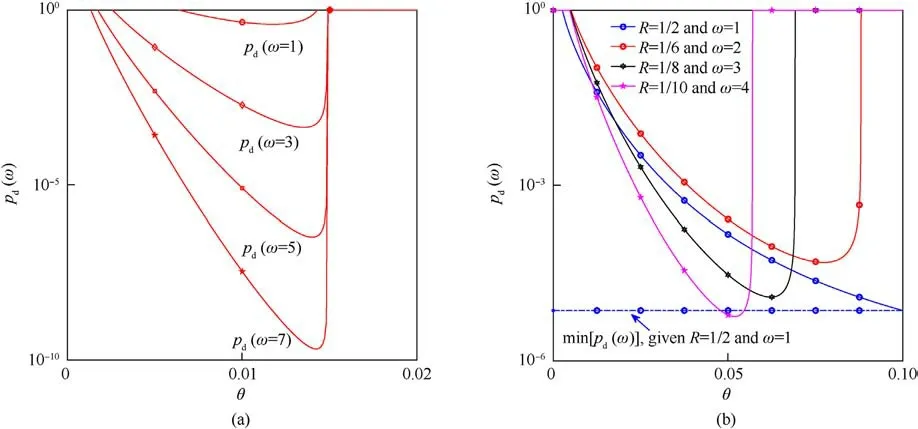
Fig.5.The timeliness of NCM1 evaluated in terms of pd（w）.

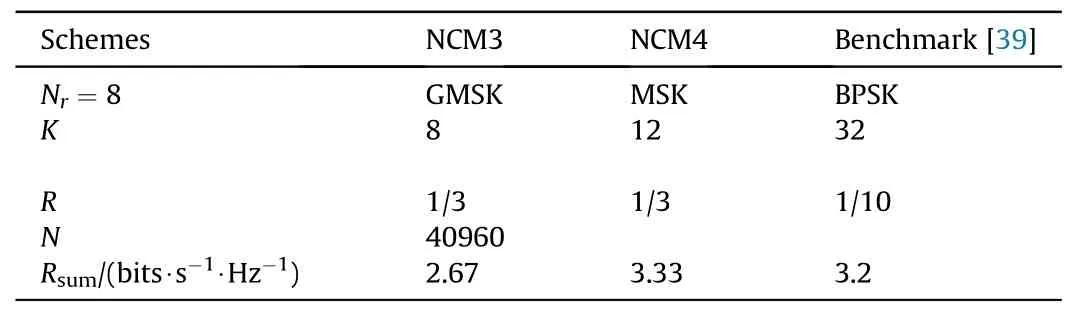
Table 3 The parameters of NCMs.

Fig.6.BER comparison of NCMs and MIMO-NOMA based on IRA [39].

In proceeding discussion, the focus has been dedicated to high rate transmission, while the performance in low rate regime is wondered.To this end,two NCMs of low sum rate are evaluated and compared with the method presented in Ref.[39].As summarized in Table 3,two NCMs are configured to deliver 2.67-3.33 bits/s/Hz using REP,while CC is not considered to make sure K ≥Nrsuch that the power allocation can be used.

The results are presented in Fig.6, where the parameters of irregular repeat-accumulate code(IRA)can be found in Table 1[39].As mentioned earlier,the performance of IRA degrades significantly over block fading channels,i.e.,the gaps to the capacity and NCM3 are respectively ≈12 dB and ≈6 dB, even NCMs offer slightly higher sum rate than IRA does.The reason is two folds.First,block fading bottlenecks the performance due to frequent occurrence of deep fading in low transmit power regime.Similar results were also discovered in Ref.[43].Second, practical MIMO-NOMA is typically interference-constrained.That being said, the performance degrades with increasing K if Nrkeeps constant.As can be observed,the required Eb/N0increases from ≈-3 dB to ≈3 dB with K increases from 8 to 32, while the resultant gaps to capacities also increase.

To summarize,the proposed NCM can take care of both high rate and low rate regime, while outperforming existing code-domain MIMO-NOMA in terms of achievable sum rate and transmit power, with very low transceiver complexity.

5.Conclusions

This paper addresses the design of integrated uplink MIMONOMA for overloaded IoMT networks, with special focuses on CPM signaling.The proposed system exploited random matrix theory to obtain a closed-form of SINR,based on which a geometric power allocation algorithm is developed.With the aid of power allocation,a single time-frequency resource block can support up to dozens of devices simultaneously.It is further proved that maximized sum rate and fairness amongst devices are offered.The proposed construction is exemplified using MSK and GMSK, two important CPMs adopted in IoMT standards such as Link-16 and JTIDS.The gap to channel capacity is effectively reduced while BER attains 10-4, and simple FECs are employed.Compared to existing solutions, the proposed scheme provides significantly improved sum rate at the expense of increased SNR gap to the capacity,which is well paid off considering the extremely low complexity and very high rate.The method presented can find pervasive applications in similar scenarios such as satellite network,where high overloading and CPM are expected.

Acknowledgments

The authors are very grateful to the editors and anonymous reviewers for their help.This work was supported in part by the National Natural Science Foundation of China(Grant Nos.61601346 and 62377039), and the Natural Science Basic Research Plan in Shaanxi Province of China(Grant No.2018JQ6044),the Ministry of Industry and Information Technology of the People's Republic of China (Grant No.2023-276-1-1), the Fundamental Research Funds for the Central Universities,Northwestern Polytechnical University(Grant No.31020180QD089), the Aeronautical Science Foundation of China (Grant Nos.20200043053004 and 20200043053005).

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.dt.2023.09.016.