Dou Hong, Wenbin Li, Yu Zheng, Yiming Li, Ning Jiang, Kebin Zhang

Ministerial Key Laboratory of ZNDY, Nanjing University of Science and Technology, Nanjing, China

Keywords:Impact damage Ultimate penetration velocity Bulge height Target penetration energy Failure modes

ABSTRACT PCrNi3MoV steel is a medium-carbon,low-alloy quenched and tempered steel that finds its applications in military gun barrels due to the high wear resistance and ablation resistance.To study the penetration and failure modes of PCrNi3MoV plates impacted by tungsten spheres, tungsten spheres of various diameters (5 mm, 8 mm, and 10 mm) were used to impact PCrNi3MoV steel plates with thicknesses of 6 mm, 9 mm, and 14 mm.The penetration performance of the spheres was analyzed for different velocities, and the ultimate penetration velocity of the plate was obtained.It was found that the primary failure modes of the PCrNi3MoV plate were compression pitting failure and shear failure.Using the dimensional analysis method,a relationship between the bulge height of the steel plate and the fragment velocity, an equation for the ultimate penetration velocity, and a relationship between the target penetration energy and the fragment velocity were obtained.Then, a projectile-target action index was proposed to describe the process of tungsten spheres with different velocities impacting target plates.The results suggested that under the same thickness of the target plate, a larger-diameter fragment required more kinetic energy to obtain the same ultimate penetration effect as a smaller-diameter fragment.The equations obtained through dimensional analysis predicted values that agreed well with experimental values, indicating that these equations can be applied to engineering applications.? 2024 China Ordnance Society.Publishing services by Elsevier B.V.on behalf of KeAi Communications

1.Introduction

PCrNi3MoV steel is a medium-carbon, low-alloy quenched and tempered steel.It not only has high transverse stiffness and plastic toughness, but also has high wear resistance and ablation resistance.It has been widely used for various heavy-duty components,such as mortar barrels, gun breeches, and bolt bodies.On the battlefield, explosive warheads are often needed to strike targets made of PCrNi3MoV steel.To increase ammunition power on the battlefield, it has become common to fill warheads with prefabricated spherical tungsten fragments.Therefore, to better understand the damage effect of tungsten fragment-containing warheads on mortars, as well as on other targets, it is critical to study the penetration and failure modes of PCrNi3MoV steel plates impacted by tungsten spheres at various velocities.The research results can provide data for design optimization of warheads, as well as for evaluating the damage effects of warheads on mortar targets.

Many studies have been conducted to investigate the penetration performance of tungsten alloy materials.For instance,Li et al.[1] compared the penetration performance of a fine-grained 95WNiFe alloy with that of conventional tungsten rod penetrators.The results showed that, due to the self-grinding behavior of fine tungsten particles,the penetration performance of the finegrained 95WNiFe alloy was better than that of the conventional tungsten rod penetrators.The W-W interface in the microstructures of the conventional tungsten penetrators had an adverse effect on the penetration performance.When a tungsten penetrator had a velocity of 1000 m/s,most of its kinetic energy was consumed by the tungsten ball breakage rather than by the penetration process [2].Based on Li's study, Hafizoglu et al.[3] investigated the ballistic performance variations of tungsten alloy fragments with changes in the sintering temperature and the Ni/Fe ratio.The results showed that the tungsten alloy fragments had the best ballistic performance and perforation capability with a 1480°C sintering temperature.In addition,many studies have explored the penetration characteristics of tungsten alloys from the perspective of material constitutive models [4,5].

Extensive research has been conducted regarding the penetration performance characteristics of tungsten alloy fragments impacting various targets, which include the ultimate penetration velocity,the penetration depth,and the bulge height[6-9].In fact,as early as the 1980s and 1990s, formulas were proposed to calculate the ultimate penetration velocity of tungsten alloy fragments.Zhu et al.[10]applied the cavity expansion resistance model[11] to a scenario in which spherical fragments penetrated a steel plate.The penetration process was divided into three stages,and a penetration equation was presented for each stage.Then, the ultimate penetration velocity of the fragments was calculated.Huang and Zhu [12] developed a formula to calculate the ultimate penetration velocity using the dimensional analysis method.Based on many of ballistic gun tests, the undetermined coefficients in the formula were obtained through multiple linear regression.This method is still one of the primary methods used in engineering models.Similar studies have been conducted successively[13-15],and relatively accurate models for the ultimate penetration velocity have been obtained.The ultimate penetration velocity was calculated by a method proposed by the Frankford Armory in the United States [16]; this method is now also a conventional method.Further, Zhang et al.[17] combined the method mentioned above with reliability theory and determined the method of calculating v100.When fragments impact a plate at a velocity higher than the ultimate penetration velocity, the fragments penetrate the plate and fly along the ballistic trajectory at the residual velocity.The relationship between the entry velocity and the residual velocity has been studied by Recht and Ipson, and a prediction model was developed.The accuracy of the prediction model was verified in subsequent studies [18-20].When fragments impact the target plate at a velocity lower than the ultimate penetration velocity,the fragments create a crater in the plate.The penetration depth is closely related to the fragment diameter,as well as the strength and thickness of the target plate.Xu et al.[21] studied plate damage conditions after fragment penetration and obtained an empirical relationship between the fragment diameter and the ultimate penetration depth.Another study found that the crater diameter on a plate was linearly related to the penetration velocity, while the penetration depth had a nonlinear relationship with the penetration velocity[22].In addition, when a fragment penetrates a plate at a speed greater than the ultimate penetration velocity,it creates a bulge in the back of the plate.The bulge effect is widely used for penetrating body armor.When a projectile impacts body armor,the ceramic plate in the body armor breaks and generates a bulge in the back,thereby causing damage to the wearer[23-25].Xu et al.[26]studied the effect of the number of layers on anti-ballistic performance for plates with equal thicknesses.The influence of the plate thickness and the number of layers on the anti-ballistic performance was studied by analyzing the plate bulge height.

When studying fragment penetration performance with respect to a target plate, it is necessary to understand the damage mechanisms present during the penetration process.Li et al.[27]studied the failure modes of 35CrMnSi steel fragments after they penetrated steel plates at different speeds.The results showed that the fragments only experienced mushrooming deformation under lowspeed penetration.As the velocity increased, the fragments experienced fracture failure, and a high-temperature region appeared under high-speed penetration conditions.Moreover, there was a localized molten area in the fracture surface.When spherical fragments penetrate a target plate,failure and fragmentation of the spherical fragments occurs in an orderly process.Liu et al.[28]systematically analyzed the failure characteristics of tungsten alloy spherical fragments penetrating low-carbon steel plates under different velocity gradients.Dikshit et al.[29] studied the penetration of steel plates with different hardness values and presented the penetration mechanism.The results showed that the impact of the plate hardness on the ballistic performance was dependent on whether the stress state was plane strain or plane stress.

It is noticeable that all of the research considered above focused on the single state of the fragment impacting the target plate,such as the height of the bulge,the ultimate penetration velocity and the relationship between the entry velocity and the residual velocity,and the ultimate penetration velocity formula and the bulge height formula are not applicable to the calculation of the penetration of PCrNi3MoV steel plates by spherical fragments.

In the present study,empirical equations were obtained through dimensional analysis to predict the bulge height, the ultimate penetration velocity, and the target penetration energy during the penetration of PCrNi3MoV steel plates by spherical fragments.Several groups of ballistic gun experiments were conducted, and the undetermined coefficients in the equations were determined by multiple linear regression.The values predicted by the proposed equations were consistent with the experimental data.The bulge height, the ultimate penetration velocity, and the target penetration energy were combined to form a projectile-target action index, which was used to describe the state of the plate under different fragment velocities.

2.Theoretical fragment penetration model

2.1.Analysis of the fragment penetration process

The interactions between the prefabricated fragments and the target are complex physical process.In the early stages of penetration, a large contact stress is generated between the fragments and the target.As the fragment velocity decreases, the plate material that is in contact with a fragment experiences a plastic flow phenomenon, during which some particles flow to the side of the contact surface.At this time,the crater ridge on the front surface of the target turns outward, forming a petal-shaped pattern.This stage is called the plastic penetration stage.With continuous fragment penetration, the compressive stress in the penetrated region of the target surpasses the shear stress.Shear failure then occurs in the penetration region,thereby forming a shearing zone.This stage is referred to as the shearing stage.Fragment penetration into the target plate is a deformation and destruction process with a high strain rate,which not only involves the strain hardening effect,but also the thermal softening effect related to an adiabatic temperature rise.Under certain conditions,this coupling effect leads to the formation of an adiabatic shear zone.After the shear zone has completely formed, the sheared block and fragments travel together in the penetration direction.This is called the plug penetration stage.After the plug is completely pushed out of the plate,the entire penetration process is complete.

In this study, based on the plastic penetration stage, the shearing stage, and the plug penetration stage classifications, the entire penetration process was divided into three conditions.The first is plate bulging.In this condition, the fragment energy is not large enough for plate penetration.After forming a crater in the front of the target,the fragments form a bulge of a certain height in the back of the target.Second, there is the ultimate penetration condition.In this state,the fragment energy is just enough for the fragments to penetrate the plate, and there is no residual energy after the perforation.Third,there is the over-penetration condition,in which, after the fragments penetrate the plate, there remains some energy with which the fragments impact the objects behind the target.All three conditions were analyzed during this study and are discussed in this paper.

2.2.Plate bulging

The penetration of spherical tungsten fragments into a plate is a relatively complex physical and mechanical process.It is accompanied by the propagation of elastic-plastic waves, microdeformation of the tungsten spheres, local deformation of the plate, and transient stress variations [30].Based on certain assumptions and the dimensional analysis method, a simplified model was developed during this study to describe fragment penetration into a carbon fiber plate.

Three primary assumptions were made in the model:

(1) All thermal effects are negligible.

(2) The spherical fragments are rigid bodies.

(3) The fragments travel in straight lines.

In the study of fragment penetration issues, the polynomial fitting method was generally used before the 20th century when developing engineering models.However, this calculation process is complicated, lacks physical meaning, and cannot describe the influences of individual physical parameters on the calculation results.Dimensional analysis, which is a tool for determining the relationships between various quantities in complex processes or physical phenomena, can better reflect the laws of physical phenomena than can traditional methods.

The penetration of spherical fragments into a plate is affected by many factors;the primary factors and their dimensions,according to Ref.[12], are shown in Table 1.By analyzing each parameter, a dimensionless equation was developed to calculate the bulge height.

Experiments have shown that the bulge height changes with the fragment velocity.A formula to calculate the bulge height was developed using dimensional analysis.Table 1 shows that there are nine characteristic parameters in the penetration process.Since the fragments were assumed to be rigid bodies, the influence of the fragment strength on the penetration process was not considered in the penetration dynamics problem.Therefore,the characteristic parameters that describe the penetration process of spherical fragments are d, ρf, h, hg, ρt, and σt.The relationship between the bulge height and the fragment velocity can be expressed by Eq.(1):

where Δhgrepresents the change in the bulge height.Eq.(1) contains three independent variables,and d,ρf,σt,and Δv were taken as basic quantities to measure each quantity in the equation.Hence,a relationship between the quantities was obtained,as shown in Eq.(2):

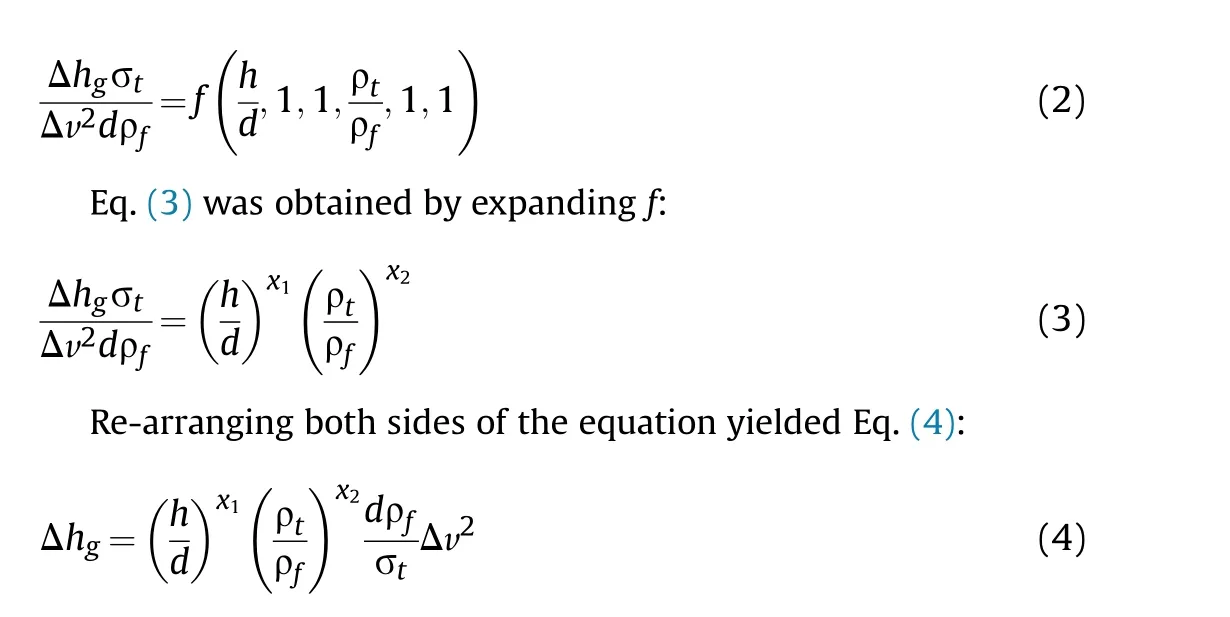
where x1and x2are undetermined coefficients.

According to the literature,there is a minimum velocity,vz,that causes bulge deformation in the plate.Therefore, the curve representing the relationship between the bulge height and the fragment velocity must pass through point (vz, 0).The bulge height equation can be expressed by Eq.(5):

2.3.Ultimate penetration

Li et al.[16]defined the fragment ultimate penetration velocity in the end effect theory as an average of the highest velocity at which fragments partially penetrate a plate and the lowest velocity at which all fragments penetrate the plate.The fragment ballistic ultimate velocity can be characterized by v50or v100.Many experiments have shown that for a given projectile-target system, v50follows the normal distribution.When the number of fragments that have penetrated is greater than or less than the number of fragments that have not penetrated,v50can be calculated using Eq.(8) or (9), respectively:

In Eqs.(8)and(9),vArepresents the average fragment velocity in the mixing zone,Npis the number of fragments in the mixing zone that have not penetrated,Ncis the number of fragments that have penetrated, vpmaxis the maximum velocity of the fragments that have not penetrated, and vpminis the minimum velocity of the fragments that have penetrated.

Many experiments are required to calculate the ultimate penetration velocity of the fragments using Eqs.(8) and (9).It is impossible to obtain the ultimate penetration velocity directly under specific projectile-target conditions.This section describes how the ultimate penetration velocity was studied using dimensional analysis based on the parameters in Table 1.

According to the parameters listed in Table 1, the ultimate penetration velocity can be expressed by Eq.(10):

where vtrepresents the ultimate penetration velocity.This equation contains three independent variables, and d, ρf, and σtcan be taken as basic quantities to measure each quantity in equation.A relationship between the quantities was obtained,as shown in Eq.(11):

2.4.Over-penetration

The energy required for fragments to penetrate a plate varies with the fragment velocity.According to the equation for the ultimate penetration velocity, an equation for the target penetration energy was developed through dimensional analysis.The primary factors that influence the process of spherical fragments penetrating a plate,along with their dimensions, are listed in Table 1.

According to the parameters,the relationship between a change in the target penetration energy and a change in the fragment velocity is shown in Eq.(17):

3.Experiments

3.1.Experimental design

The experimental setup is shown in Fig.1.The system was composed of a Φ14.5-mm ballistic gun,a gun frame,a bullet stock,spherical tungsten(93WNiFe)fragments,a bullet retractor,a highspeed camera, a steel plate, and a supporting frame for the plate.During the tests,the tungsten fragments were sealed and placed in the bullet stock.The entry velocity of the fragments was controlled by adjusting the propellant mass ratio.The maximum fragment velocity was 1500 m/s.After the fragments exited the muzzle,they separated from the bullet stock and hit the plate after passing through the bullet retractor hole, while the bullet stock was intercepted by the bullet retractor.The sabot, cartridge case and fragment required for the test are shown in Fig.2,and the sabot is made of nylon.

The penetration of tungsten fragments with diameters of 5 mm,8 mm, and 10 mm into plates with different thicknesses was studied in the experiments.The plates were composed of PCrNi3-MoV steel.The primary properties of the spherical tungsten fragments and the PCrNi3MoV steel are listed in Table 2.

3.2.Coefficient calibration

3.2.1.Calibration of the coefficients in the bulge height equation

Spherical tungsten fragments with diameters of 5 mm were used to impact gun steel plates with different thicknesses.To measure the bulge height of a plate, the plate was cut after the experiment.As shown in Fig.3, the axial displacement from the center point of the impact surface,i.e.,the maximum deformation,was taken as the bulge height,hg.When the fragments did not pass through the plate,a larger bulge height indicated greater damage to the plate.

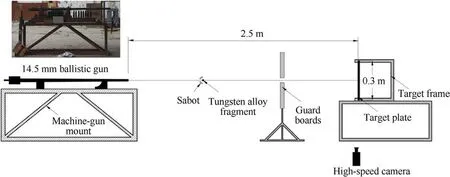
Fig.1.Experimental setup.

Fig.2.Components used in the ballistic experiments.

Table 2 Material properties of the prefabricated fragments and steel plates[31].

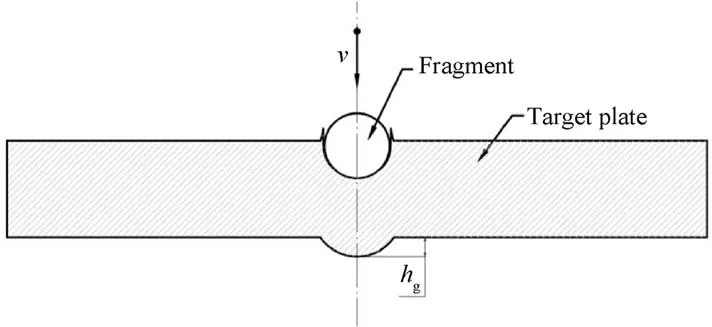
Fig.3.Schematic diagram of a fragment penetrating a plate.

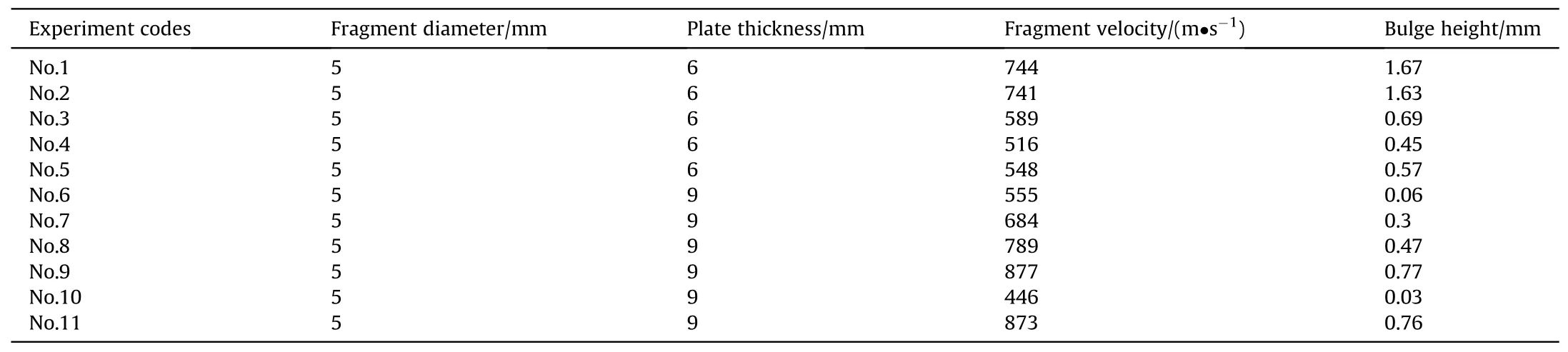
Table 3 Bulge heights for spherical fragments impacting PCrNi3MoV target plates.

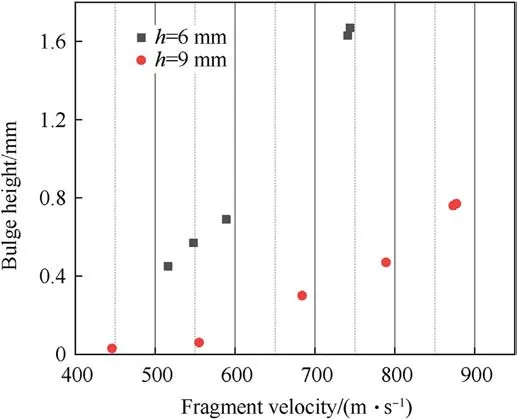
Fig.4.Relationship between the bulge height and the fragment velocity.

Table 3 shows that the bulge height increased with increases in the fragment velocity.Fig.4 shows the results more intuitively.For a given projectile-target system,the bulge height had a nonlinear relationship with the fragment velocity.When both the fragment diameter and the fragment velocity remained constant, a greater plate thickness produced a smaller bulge height.When the fragment diameter was constant,a greater plate thickness led to more curvature in the bulge height curve with respect to the fragment velocity.

Eq.(7) was used to process the data in Table 3 using the least squares method;the relationship between the bulge height and the fragment velocity could thus be obtained, as shown in Fig.5.The fitting coefficients and fitting accuracy for different projectile-target systems are shown in Table 4.

Fig.5 shows that the confidence intervals were narrow for both plate thicknesses and that the test data were all within the confidence intervals, indicating that the tests were consistent and accurate.The fitting coefficient values listed in Table 4 show that as the plate thickness increased,fitting coefficient A1decreased,while vzincreased.This result is consistent with the overall variability of the projectile-target system shown in Fig.5.In addition,the fitting accuracy was greater than 95%,which suggests that it was accurate to fit the bulge height data using the function y = A1(x-vz)2, and that the needs of practical engineering calculations were met.

The undetermined parameters in Eq.(7) could be calculated using the fitting coefficients, A1, and vz, as shown in Table 5.

3.2.2.Calibration of the coefficients in the ultimate penetration velocity equation

Table 6 lists the ultimate penetration velocities of fragments with different diameters that penetrated gun steel plates of different thicknesses.

Table 6 shows that the ultimate penetration velocity changed with different fragment diameters and different plate thicknesses.Fig.6 shows the relationship between the relative thickness, h/d(plate thickness divided by fragment diameter),and the ultimate penetration velocity.As the relative thickness increased, the ultimate penetration velocity increased accordingly.

By substituting the experimental data from Table 6 into Eq.(16),y1= 0.9177 and y2= -1.4648 were obtained.The resultant expression is presented as Eq.(27):

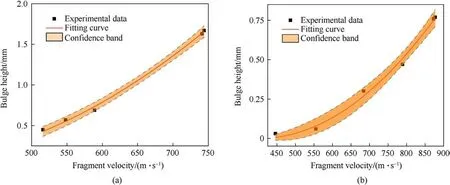
Fig.5.Relationship between the bulge height and the fragment velocity: (a) Condition 1 (5-mm fragment diameter and 6-mm plate thickness); (b) Condition 2 (5-mm fragment diameter and 9-mm plate thickness).

Table 4 Fitting coefficients and fitting accuracy for different projectile-target systems.

Table 5 Fitted values of x1, x2, x3, and x4.

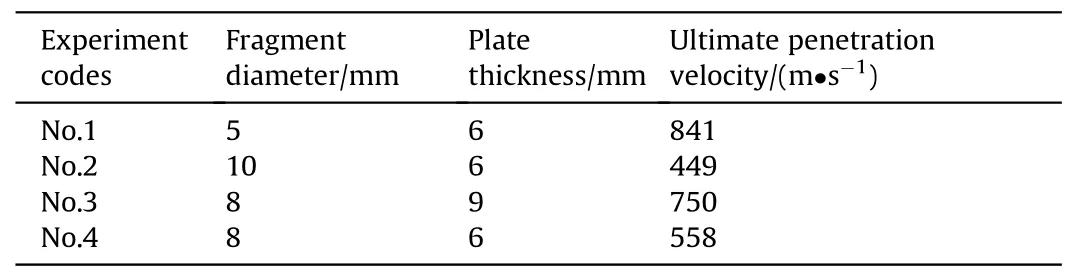
Table 6 Ultimate penetration velocities of spherical fragments under different conditions.

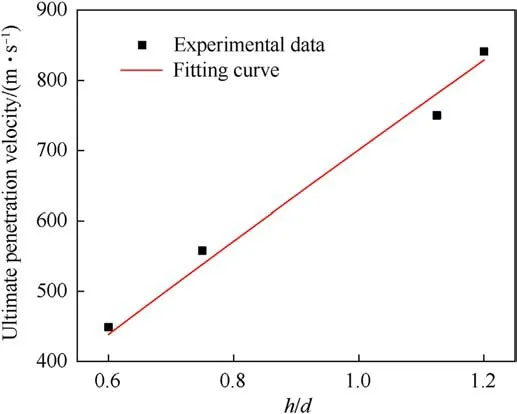
Fig.6.Relationship between the ultimate penetration velocity and the relative thickness, h/d.

3.2.3.Calibration of the coefficients in the target penetration energy equation

To determine the variations in the target penetration energy of fragments with different velocities in the same projectile-target system, multi-gradient velocity penetration tests were conducted,and the results are shown in Table 7.Under the same projectile-target conditions,a larger entry velocity indicated that a higher energy was required to penetrate the target.

Additionally,Eq.(22)shows that A2and B are constant for given a given set of projectile-target conditions, and that the target penetration energy increased with increases in the penetration velocity.Eq.(22) was used to fit the data in Table 7 by the least squares method,and a relationship between the target penetration energy and the fragment velocity was obtained,as shown in Fig.7.The fitting coefficients and fitting accuracy for different projectile-target conditions are shown in Table 8.

Fig.7 shows that the target penetration energy increased as the penetration velocity increased, thereby increasing the difference between the ultimate penetration energy and the target penetration energy test value.This means that when a fragment penetrates a plate at a velocity greater than the ultimate penetration velocity,the error in the residual velocity calculated using the ultimate penetration energy will increase with increases in the fragment velocity.For Condition 1, when the fragment velocity increased by 33%, the error between the target penetration energy and the ultimate penetration energy increased by 70%.For Condition 2,when the fragment velocity increased by 70%, the error between the target penetration energy and the ultimate penetration energy increased by 159%.

A comparison of the ultimate penetration energy with the target penetration energy test data indicates that the fragment entryvelocity significantly influenced the required target penetration energy.There are certain limitations in characterizing the antiballistic performance of materials using the ultimate penetration velocity, but the target penetration energy formula provides more accurate results.

Table 7 Experimental results for spherical fragments penetrating plates at different velocities.

Fig.7.Relationship between the target penetration energy and the fragment velocity:(a)Condition 1(5-mm fragment diameter and 6-mm plate thickness);(b)Condition 2(8-mm fragment diameter and 9-mm plate thickness).

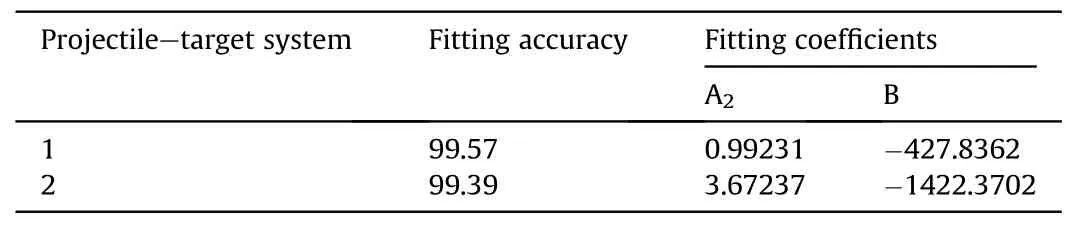
Table 8 Fitting coefficients and fitting accuracy for different projectile-target systems.

The fitting coefficients in Table 8 show that for different projectile-plate systems, as the ratio of the fragment diameter to the plate thickness increased, the magnitudes of the fitting coefficients also increased; this result is consistent with the overall system trend depicted in Fig.7.In addition,the fitting accuracies for the different systems were greater than 95%,which suggests that it was accurate to use Eq.(22) to fit the fragment target penetration energy and that the needs of practical engineering calculations were met.

After the A2values were obtained for both conditions,y3= 3.1441 and y4= -2.1387 were obtained.The resultant expression is given as Eq.(28):

3.3.Experimental verification

3.3.1.Bulge height

To verify the bulge height equation, fragments with different diameters (5 mm, 8 mm, and 10 mm) were used to impact plates with different thicknesses, and a high-speed camera was used to measure the fragment velocity.

Table 9 presents the experimental bulge height results and the corresponding calculated values,as well as the error between them.The average error between the calculated and experimental values was approximately 7.303%, and the maximum error was 14.43%.Hence, the bulge height equation developed during this study is highly accurate and meets the needs of practical applications.

Figs.8 and 9 present the variations in the bulge height with the fragment diameter and the plate thickness, respectively.The intersection of the curve and the horizontal axis is the point of minimum deformation velocity, vz.When the fragment velocity is less than vzfor a projectile-target system,no bulge deformation is produced on the back of the plate.When the fragment velocity isgreater than vzfor a projectile-target system, bulging occurs.In addition, Fig.8 shows that when fragments of different diameters penetrated plates at the same velocity, a larger fragment diameter produced a larger bulge height.When fragments of the same diameter penetrated plates at the same velocity,a thicker plate had a smaller bulge height.When fragments with different diameters penetrated plates, to obtain the same bulge height, a larger fragment diameter indicated that a greater kinetic energy was required,and vice versa.

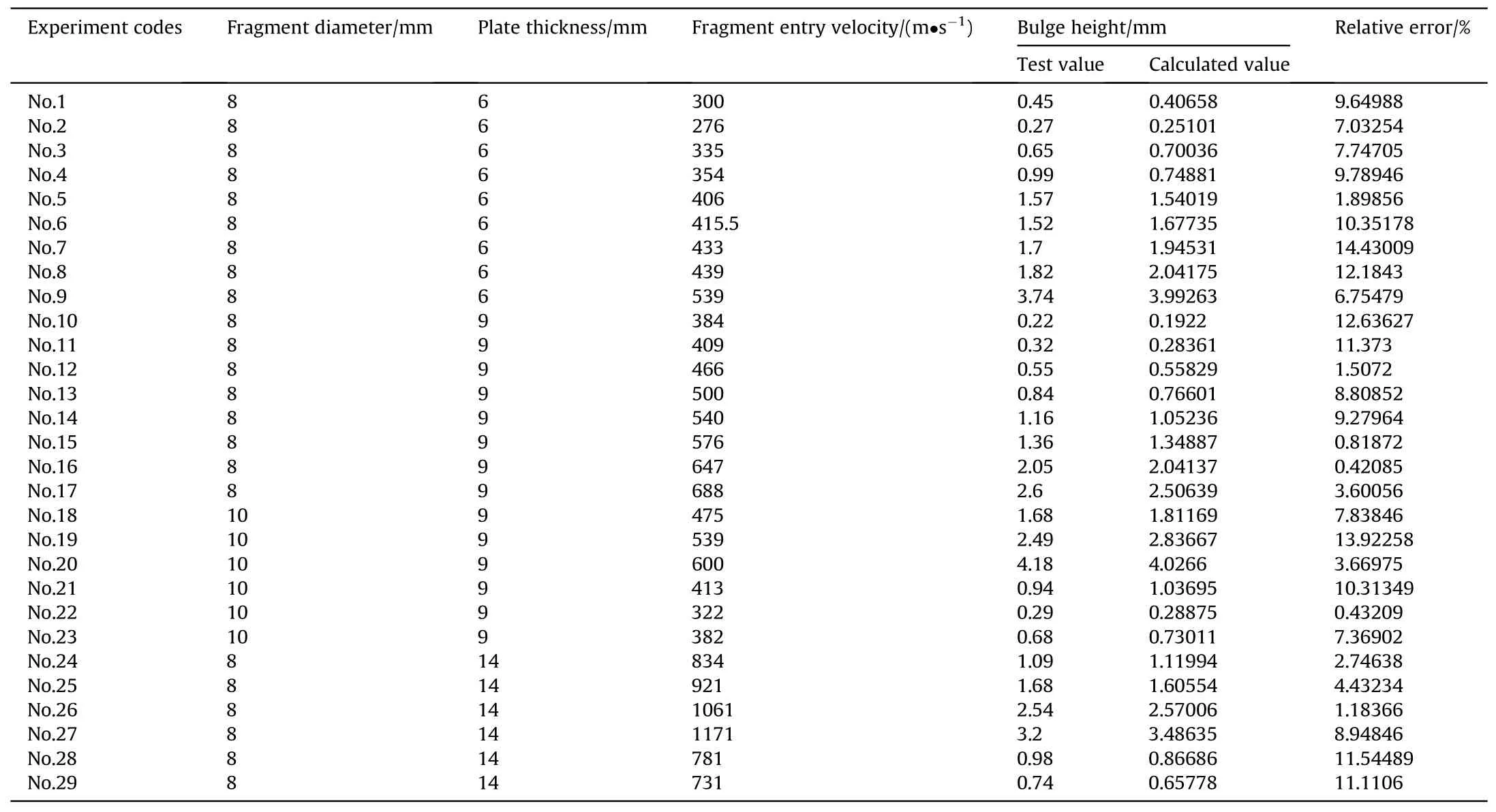
Table 9 Experimental data gathered for fragments penetrating steel plates.

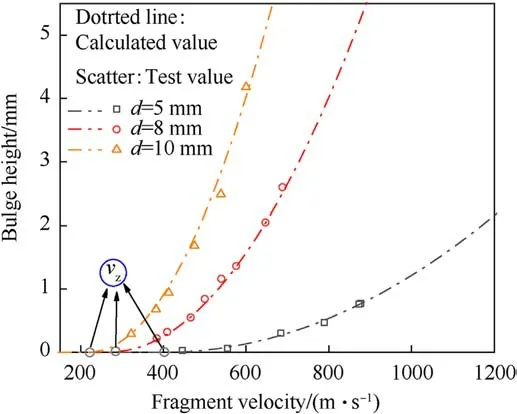
Fig.8.Bulge height when fragments of different diameters penetrated a 9-mm plate.

3.3.2.Ultimate penetration velocity

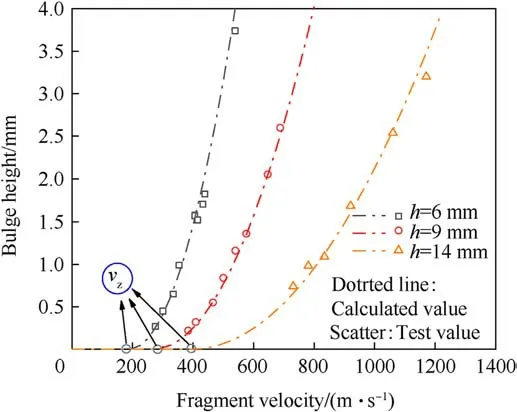
Fig.9.Bulge height when 8-mm fragments penetrated plates of different thicknesses.

To verify the ultimate penetration velocity equation, fragments of different diameters (5 mm, 8 mm, and 10 mm) were used to impact PCrNi3MoV steel plates of different thicknesses,and a highspeed camera was used to measure the fragment velocity.

Since Eq.(17) was obtained through dimensional analysis and fitting of experimental data, it is applicable for tests in which spherical tungsten fragments penetrate gun steel plates.The parameter ranges are v ＜1300 m/s and 0.6 ＜h/d ＜1.8(see Fig.10).The experimental ultimate penetration velocity results and the corresponding values calculated using Eqs.(17) and (29) [32] are listed in Table 10.

Fig.10.Comparison between the experimental and calculated values of the ultimate penetration velocity of spherical tungsten alloy fragments penetrating PCrNi3MoV steel plates.

in Eq.(29),k is an experimental coefficient,which is equal to 0.002 for spherical fragments, m is the fragment mass (kg), and S is the plate area that is covered by fragments (m2).

Table 10 shows that the average error between the ultimate penetration velocity calculated using Eq.(17) and the measured results was 5.75%, and that the maximum error was 9.35%.The average error between the values calculated using Eq.(29)and the measured results was 62.05%,and the maximum error was 65.03%.Thus,the equation developed during this study using dimensional analysis was more accurate.

3.3.3.Target penetration energy

To verify the target penetration energy equation, fragments of different diameters(5 mm,8 mm,and 10 mm)were used to impact PCrNi3MoV steel plates of different thicknesses, and a high-speed camera was used to measure the fragment velocity.

Table 11 presents the experimental target penetration energyresults and the corresponding calculated values,as well as the error between them.The average error between the calculated target penetration energy and the measured values was approximately 4.57%, and the maximum error was 10.601%.Therefore, the equation developed during this study using dimensional analysis is highly accurate and meets the needs of practical engineering applications.

Table 10 Experimental and calculated results for the ultimate penetration velocity.

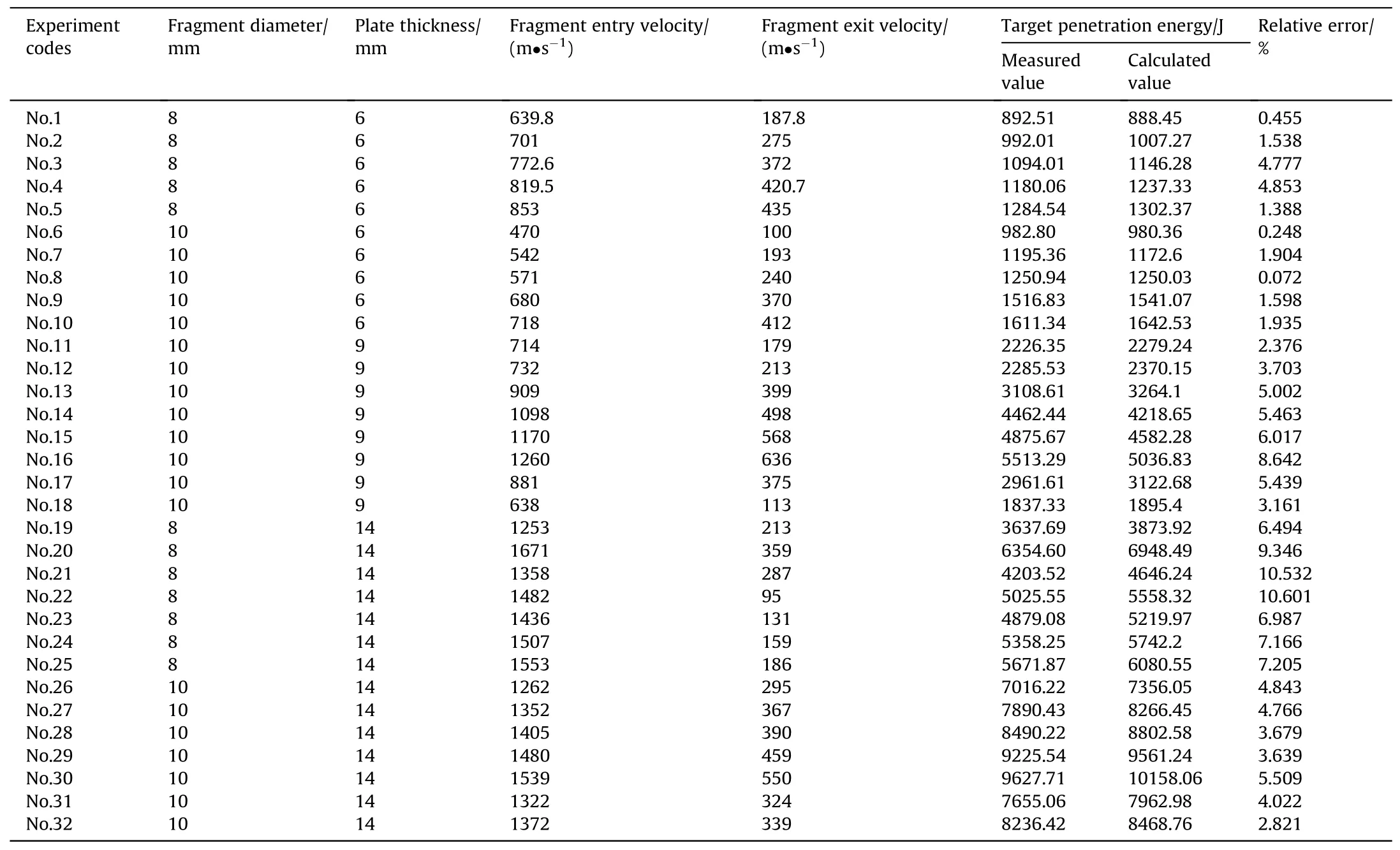
Table 11 Experimental and calculated results for the target penetration energy.

Fig.11 shows that intersection of the fragment target penetration energy and fragment kinetic energy curves is the ultimate penetration point,of which the abscissa is the ultimate penetration velocity and the ordinate is the ultimate penetration energy.When the fragment velocity is lower than the ultimate penetration velocity,the energy required to penetrate the plate is greater than the fragment kinetic energy;therefore,the fragment cannot penetrate the plate.However,when the fragment velocity is greater than the ultimate penetration velocity, the fragment kinetic energy is greater than the energy required to penetrate the plate, and the fragment can penetrate the plate.The area under the intersection of the two curves represents the residual energy after penetration.According to Fig.11,when fragments penetrated plates of different thicknesses at the same velocity,a thicker plate indicated that more energy was required.Fig.12 shows that when fragments of different diameters penetrated a plate at the same velocity,a larger fragment had a greater target penetration energy.If fragments of different diameters penetrated a plate with the same kinetic energy, a larger fragment diameter indicated that more energy was required for the fragment to penetrate the plate.

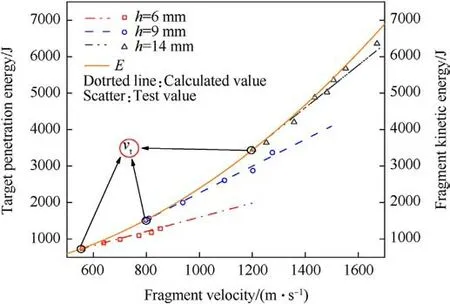
Fig.11.Target penetration energy and fragment kinetic energy when 8-mm fragments penetrated plates of different thicknesses.

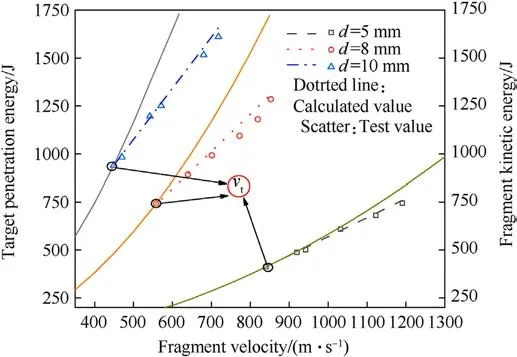
Fig.12.Target penetration energy and fragment kinetic energy when fragments of different diameters penetrated 9-mm plates.

3.4.Projectile-target action index

The analysis presented above indicates that as the velocity of the tungsten fragments increased, the interactions between the fragments and the plate changed accordingly.However, there is currently no standard formula to describe these interactions.In this study,a projectile-target action index,I,was proposed to describe the interactions between the fragments and the plate.The equation for I is given in Eq.(30):

When I=0,the fragments impacting the plate will not produce a bulge.When 0 ＜I ＜1, a bulge will be formed on the back of the plate.When I = 1, the fragments are in the ultimate penetration state.When I ＞1, the fragments penetrate and pass through the plate.Vnrepresents the velocity threshold for producing a bulge.When the fragment velocity is greater than vnbut less than vz,since the plate is in the shear failure mode,the bulge height can no longer be described by Eq.(7).Therefore, it is assumed that under this condition, the projectile-target action index increases linearly.Fig.13 presents a schematic diagram of the variation in the projectile-target action index, I, as a function of the fragment velocity.

Fig.13.Changes in the projectile-target action index, I, with the fragment velocity.

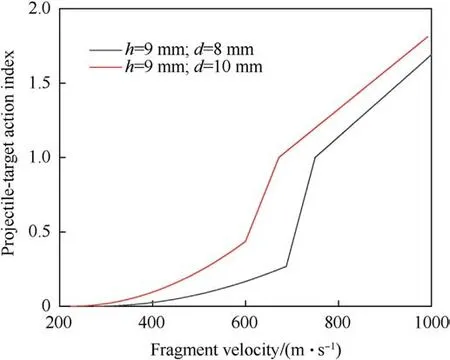
Fig.14.Changes in the projectile-target action index with the fragment velocity for fragments of different diameters.

To determine the relationship between the projectile-target action index and the fragment velocity under different projectile-target conditions, experimental data were substituted into Eq.(30) to obtain Fig.14.Using the experimental data, the variation in the projectile-target action index was analyzed for tungsten fragments with diameters of 8 mm and 10 mm penetrating a 9-mm plate at different velocities.When the fragments impacted the plate at a low velocity, since the plate failure mode was inertial compression, the projectile-target action index increased slowly with increases in the fragment velocity.When the fragment velocity reached the bulge threshold, the plate failure mode was primarily shearing.At this time, a bulge was superimposed on the lateral displacement of the plug; therefore, the projectile-target action index increased rapidly.According to the experimental data, vn≈0.9vt.In addition, Fig.14 shows that the projectile-target action index increased more rapidly for fragments with larger diameters, which is consistent with the theoretical analysis presented above.

4.Conclusions

In this study,dimensional analysis was used to obtain empirical equations to predict the bulge height, the ultimate penetration velocity, and the target penetration energy of spherical tungsten fragments penetrating PCrNi3MoV steel.Experiments were conducted using tungsten fragments of different diameters to impact gun steel plates of different thicknesses.Quantitative data for the ballistic performance were obtained.The primary conclusions from this study are provided next.

(1) When a tungsten fragment penetrated a gun steel plate at a velocity lower than the ultimate penetration velocity,a bulge formed on the back of the plate, and the relationship between the bulge height and the penetration velocity was nonlinear.When fragments of different diameters penetrated a plate at the same velocity, a larger fragment diameter produced a greater bulge height.When fragments of the same diameter penetrated plates of different thicknesses at the same velocity, a larger thickness produced a smaller bulge height.To obtain equal bulge heights when fragments of different diameters penetrated a plate, a larger fragment diameter required more fragment kinetic energy.When fragments had equal amounts of kinetic energy, a smaller fragment diameter caused a larger bulge height.When tungsten fragments penetrated a gun steel plate at a velocity higher than the ultimate penetration velocity,the fragments had a certain residual velocity after passing through the plate.

(2) In this study,the over-penetration behavior was described by the target penetration energy.When the target penetration energy was equal to the fragment kinetic energy, the fragment was in the ultimate penetration state, in which the target penetration energy increased linearly with increases in the fragment velocity.

(3) This article obtains the relationship between the bulge height and the fragment velocity, an equation for the ultimate penetration velocity, and a relationship between the target penetration energy and the fragment velocity were obtained.The calculated values agreed well with experimental values, with errors within 15%, and a projectile-target action index was proposed, which can better describe the interactions between the fragments and the plate.Therefore, the equations developed in this study meet the needs of practical engineering applications.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.