D A Baghdasaryan ,V A Harutynyan ,E M Kazaryan and H A Sarkisyan,*

1 Russian-Armenian University,H Emin 123,0051,Yerevan,Armenia

2 Institute of Applied Problems of Physics,25 Nersisyan St,0014,Yerevan,Armenia

Abstract This paper theoretically studies the impurity states and the effects of impurity concentration and configuration on the optical,electrical,and statistical properties of CdSe nanoplatelets (NPLs).An image charge-based model of electron-impurity interaction is proposed.The charge-carrier energy spectra and corresponding wave functions depending on the impurity number and configuration are calculated.The electron binding energies are calculated for different NPL thicknesses.It is shown that the image charge-based interaction potential that arises due to the dielectric constants mismatch is much stronger than the interaction potential that does not take such a mismatch into account.Also,it is demonstrated that the binding energies are increasing with the number of impurities.We calculate the canonical partition function using the energy levels of the electron,which in turn is used to obtain the mean energy,heat capacity,and entropy of the non-interacting electron gas.The thermodynamic properties of the non-interacting electron gas that depend on the geometric parameters of the NPL,impurity number,configuration,and temperature are studied.

Keywords: nanoplateletes,thermodynamic properties,impurity states

Introduction

Along with many low-dimensional semiconductors fabricated and used on the basis of such structures as quantum wells,quantum wires,and quantum dots (see,for example,[1–6]and literature thereto),a large number of both experimental and theoretical works have been devoted to studying the properties of so-called semiconductor nanoplatelets(NPLs)in the last decade [7–11].NPLs are planar quasi-two-dimensional (quasi-2D) structures with pronounced charge carrier size quantization in the direction perpendicular to the sample plane,as well as the presence of organic environment and lateral confinement [7–11].The specific behavior of charge carriers in such structures is such that,in NPLs,unlike quantum dots,the confinement of charge carriers is much stronger in the stacking direction than in the other two NPL dimensions [7–11].There have been reports about the successful synthesis of atomically flat quasi-2D colloidal nanoplatelets made of CdSe,CdS,and CdTe,which have welldefined thicknesses ranging from 4 to 11 monolayers [10].

As a result,NPLs exhibit a number of unique properties that make it possible to observe such physical phenomena,the manifestation of which is fundamentally impossible not only in massive samples but also in the ‘traditional’ low-dimensional semiconductors listed above: for example,large exciton binding energies,a large absorption cross-section narrow emission spectrum,and rapid photoluminescence lifetimes[7–14].Particularly,the significant confinement in the growing direction of quantum NPLs results in a remarkably narrow emission spectrum,with a full width at half-maximum in the range of tens of meVs at room temperature,as reported in [10].Due to these particularities,NPLs can be considered building-block candidates in various applications,including light-emitting diodes [15],transistors [16],detectors and phototransistors [11–13],and solar light concentrators [17].

The thickness of NPLs can only be changed by discrete numbers of atomic layers,which limits their tunability in terms of energy spectra and other physical properties.To address this limitation,various mechanisms have been proposed,such as doping,the use of alloyed NPLs,and the application of external electrostatic or magnetic fields,to enhance the tunability of NPLs.One of the effective and powerful external modulating factors involves doping the sample with one or another type of impurity [18–21].Impurity doping has long been challenging from a technological point of view and Mn doping was the most used.Recently,researchers’ efforts have been focused on incorporating wider types of impurity doping [15].It should be mentioned that today,developments in this direction have made controllable incorporation of different kinds of impurities possible [15,18–21].For example,in [20],the authors investigated the controlled doping with silver in CdSe 2D NPLs in the intermediate doping range of 1 to 100 Ag dopants per nanoparticle.The research indicates that,at low doping levels,Ag functions as an n-type dopant and switches to a p-type dopant when incorporated in large amounts.Therefore,in the process of doping,the properties of the sample essentially depend on the doping level (impurity concentration).

The presence of a larger amount of impurities can lead to a significant rearrangement of the carrier energy spectrum,which will affect the physical characteristics of the studied structures.In this regard,it is of interest to study the electronic states in an NPL in the presence of several impurity centers.This type of problem is quite complex;therefore,one has to use simplified models to describe such systems.The simplest system that can be considered is the hydrogen molecule ion analog,when one electron is associated with two impurity centers.Quantum-mechanical descriptions of such systems are well-developed and have been the subject of research for a long time in molecular physics [22].However,the presence of a larger number of impurity centers can provide a richer picture of the physical phenomenon of an electron gas under quantum confinement conditions.

Knowledge of the energy spectrum of the electron allows us to study various characteristics of the NPLs under study.In particular,it allows us to investigate the thermodynamic characteristics of a non-interacting electron gas,by firstly considering the influence of impurity concentration and secondly,by considering polarization effects.The study of the statistical characteristics of quantum dots encompasses a large number of works.In particular,in[23],the authors calculated the statistical properties of the electron gas in double-ring quantum dots.In [24,25],core/shell nanofiber or transitionmetal dichalcogenides(TMD)monolayers were considered as the system to investigate statistical properties.Alternately,such effects are also investigated in quantum dots [26–28].However,it is interesting to study statistical properties in NPLs,by considering the hybrid nature of the spectrum,especially the fact that polarization effects are strongly pronounced.

This work aims to theoretically study the effects of hydrogenic impurity consternation on the optical,electrical,and statistical properties of CdSe NPLs.At the same time,we consider a simplified model when the interaction between electrons is neglected,and the considered impurity consternation and system configurations are such that the electron does not localize near a specific impurity center.

Theory

Multi-impurity states

Let us start with the one-electron problem considered within the effective mass framework.The electron is confined in the NPLs with a number of impurities located in random positions.The Hamiltonian of the electron has the following form:

where Δxy,μeand Δz,μzeare the effective mass and Laplacian of the electron in the XY plane and along the stacking direction,respectively.Here,the particle potential energy of the electron consists of the sum of all Coulomb interactions between an electron and impuritiesVe-imp(x,y),one-particle confining potential energies appearing due to the conduction and valence band offsetsVconf(z),Vconf(x,y) confining potential in the lateral plane,and the self-energy correction provided by the mismatch of the dielectric constants in the regions of a barrier resulting from the interaction of the electron with image charges in a dielectric mediumVself(z):

The confining potential defined by the band offset between the NPL and its surrounding material is taken as a finite potential well:

Here,V0is the depth of the potential well.Some of the material parameters that are considered are shown in table 1.

In such structures,the effects of polarization in the z-direction cannot be ignored due to the significant difference in the dielectric constant between the NPL and the surrounding materials.Different approaches have been used to consider the polarization effects.The description of this phenomenon was successfully produced using Ritova andKeldysh formulas [30].The Ritova–Keldysh potential has been widely used to describe the interaction between charged carriers in TMDs,phosphorene,and other 2D structures[31].With the development of both fabrication technologies and corresponding theoretical descriptions,the generalization of such an approach has been made that also includes the generation of self-potential[32].We have followed the approach used in [32] by implying the image-charge method.In this case,Lz＜＜Ly.In the NPLs,we will not consider image charges on the sides because in-plane image charges are located far from the electron and their effect is much less than in the z-direction.The image-charge method can be used to correct both the confinement potential and the self-induced polarization.If the electron is located at position z,then the image charge with index m is located at the following positions along thez-axis:

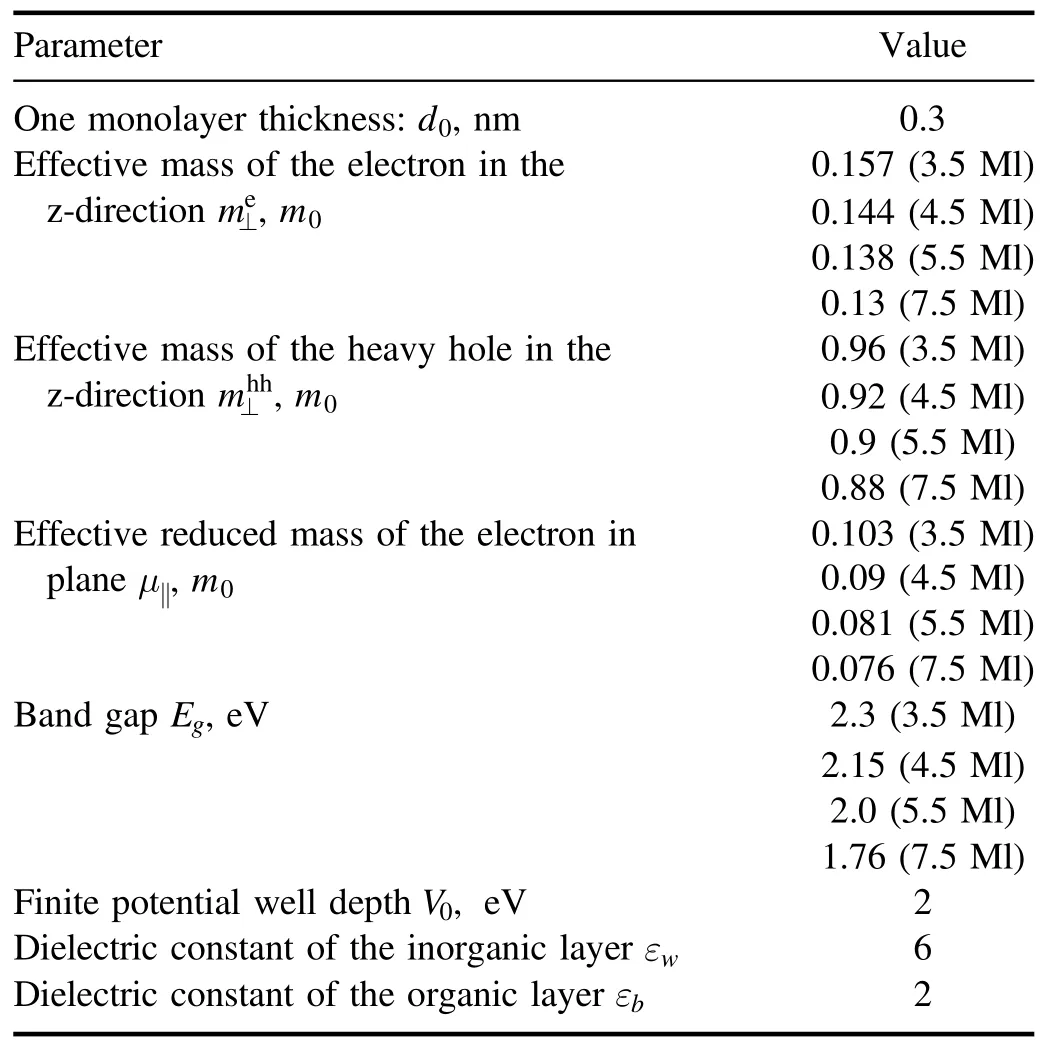
Table 1.Material parameters of the CdSe NPLs.Here,some parameters depend on the number of monolayers(ML).See[29]for reference.

The values of image charges can be obtained by applying continuity conditions for the electrostatic potential and normal component of the displacement vector at the interfaces.These image charges (with the valuesem) take the following form[32]:

For example,for the CdSe NPLs that are considered here,εw=6is the dielectric constant of the inorganic layer,andεb=2is the dielectric constant of the inorganic spacer.The calculated self-potentials using formula (6) show divergence at the layer interfaces.To solve this problem,the ‘shifted mirror faces’ procedure can be applied,which involves introducing shifting parameters.It has been previously observed that the presence of such a parameter has a negligible effect on the single particle wave functions in the stacking direction and,consequently,on the exciton binding energy [32].

To proceed further,we apply the adiabatic approximation to separate slow in-plane motion and fast motion in the growth direction [29,33].The limit of validity of the adiabatic approximation can be determined by comparing the energies due to size quantization and Coulomb interaction.It has been shown that this approximation is very precise for the case of several atomic layer thicknesses [33].Here,we will not consider the exciton effects,but only concentrate on the behavior of the electron in the effective field of many impurities.Therefore,we can consider the Schr?dinger equation that describes the motion of the electron,contrary to the case of the exciton.We seek the electron wave function via the following ansatz:

whereψ(z)is the electron wave functions in the z-direction,andψ⊥(x,y)is the wave function of in-plane dynamics.The motion in the z-direction is confined with bothVconf(z) andVself(z):

The in-plane electron motion of the electron is described by the following equation:

According to adiabatic approximation,the Coulomb interaction is averaged over the particle’s fast motion in the z-direction.Polarization effects will also affect the electron–impurity interaction potential;the standard Coulomb potential will be replaced with the following expression,where we consider the positions of all impurities in the z-direction to be

Here,thexi,yiis the position of individual impurity.Note that thedepends on the configuration of impurities(allNfixed positions): we just do not write these dependent variables for simplicity.

Figure 1 shows a schematic view of the considered problem,the energy profile,and the corresponding electron densities.

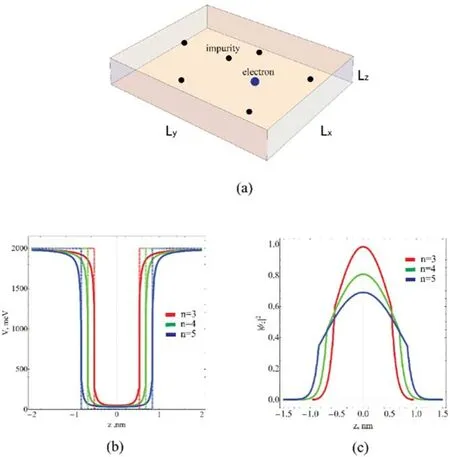
Figure 1.(a)A schematic view of the considered system.The energy profileVconf (z )+Vself (z ).The dashed line represents the confinement potentialVconf(z ) without the self-potential correction (b) and the corresponding electron probability density in the z-direction (c).Here,n is the number of monolayers.

Figures 1(b) and(c) show the considered problem of the fast subsystem in the z-direction.The effect of the selfpotential created due to dielectric coefficient mismatch is twofold:first,it shifts the lowest energy,making the depth of the potential a little less deep,and second,it smooths the energy profile near the interfaces.The penetration of the electron in the regions outside the potential will become more significant if the image charges are considered.Also,one can see the probability density curves change the slope on the interface points.Let us now present the calculation of the results,illustrating the behavior of the electron–impurity interaction potential curve with and without taking the polarization effects into account.

In figure 2 the dependencies ofare demonstrated.Figure 2.(a) shows the dependence of theon the in-plane distance between the electron and an impurity.As can be seen,consideration of the dielectric mismatch effects makes the binding between the electron and impurity much stronger and more long-range.This leads to a change in the electron localization region in in-plane motion,which significantly affects the electron in-plane wave function and binding energy.The analogous situation is discussed in[29](see figure 2(a)).It should be mentioned that in[33],the binding energy of the attractive Coulomb potential computed in such a model shows good agreement with experimental data.However,the potential created by several impurities in the XY plane significantly changes if the polarization effects are considered.Due to the long-range behavior of the potential,the interplay of individual impurity potentials becomes much more vivid,and coupling between the electron also increases (this fact is demonstrated in figures 2(b)and(c)).Figures 2(b)and(c)show the density plot of the multi-impurity potential in the NPL of size 10×15 nm,and figures 2(d)and(e)represent the 3D plot of the same potential.Let us move on to discussing the dynamics of the electron in the XY plane in the considered physical model.

Figure 3 demonstrates the in-plane electron properties.Figures 3(a),(d),and (g) show the first six states of the electron density in the NPL plane for: randomly located impurities (a);semi-random impurities,meaning that some random noise is added to the rectangular lattice(d);and when the impurities are located in the rectangular lattice points (g).Figures 3(c),(f),and (i) show the dependence of the binding energy of the electron on a number of impurities;the specific number of impurities can be realized in infinitely many different configurations.We average over five different configurations.Each data point is represented with the standard deviation of the binding energy values for different configurations,except when impurities are strictly located in the lattice points.The value of such a deviation is decreasing with the randomness level decrease going from case (c) to (i).As seen from that graph,the binding energy increases with the number of impurities in all the cases.The resulting potential of the impurities that are independent of the specific impurity’s distribution configuration becomes deeper,and correspondingly affects the binding energy of the electron.Moreover,figures 3(c),(f),and (i) illustrate the fact that the polarization makes the interaction of the electron with the impurity much stronger and long-range.The slope of the binding energy dependence on the number of the impurities curve is much larger than in the case of the Coulomb potential.Figures 3 (b),(e),and (h) show the energy level diagram for such states.As can be seen,with the increase of the order in the system,the states with close energies appear due to the rise of additional symmetry (both impurity lattice and periodic).This leads to energy level closeup and level degeneration in the lattice case(see figures 3(b),(e),and(h)).

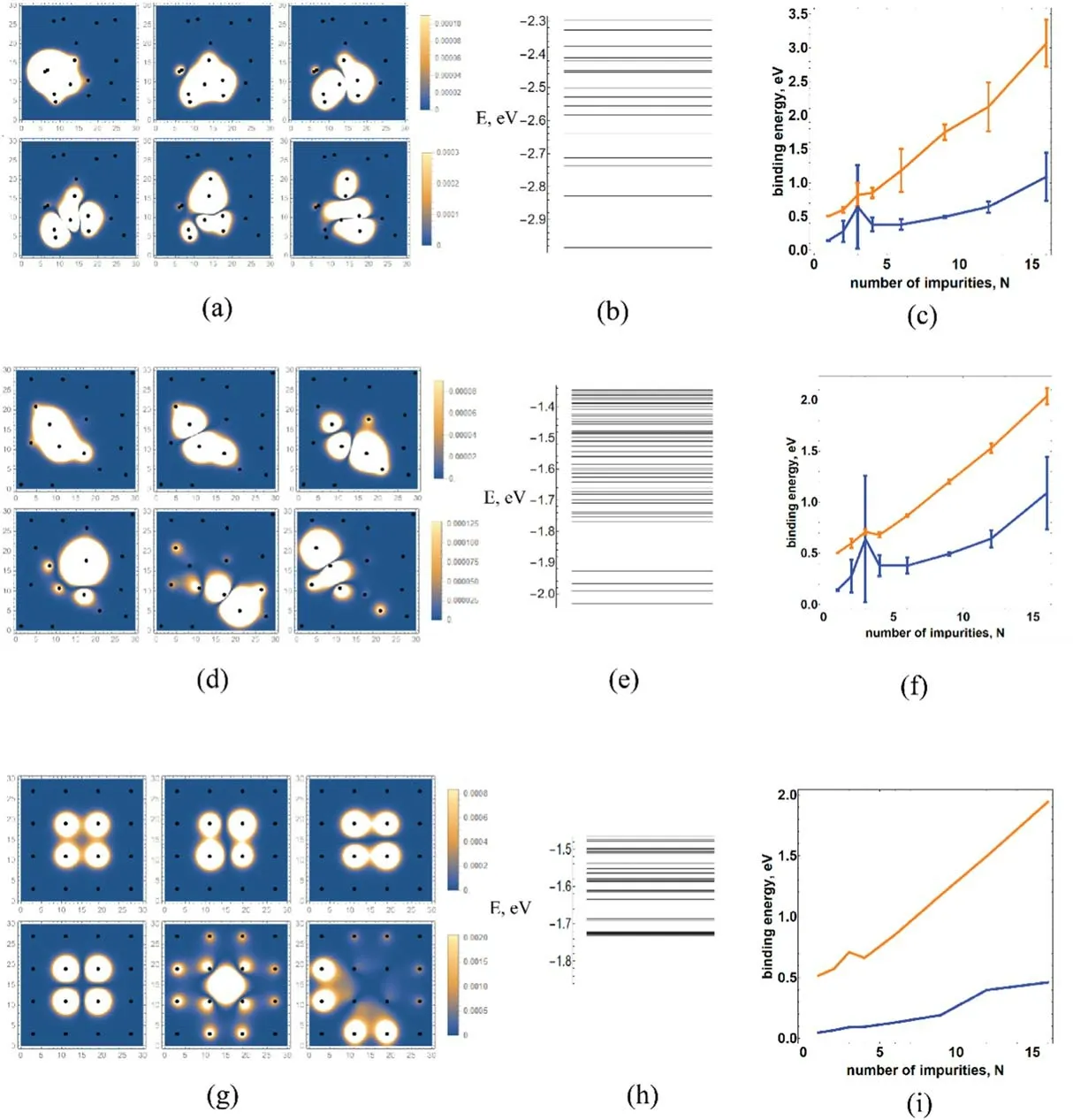
Figure 3.In-plane electron dynamics.The in-plane probability density of the electron in the first six in-plane states for the number of impurities N=16(a),(d),and(g),the corresponding energy levels(b),(e),and(h),and the dependence of the binding energy on the number of the impurities for both cases of considering using the polarization corrected electron–impurity interaction(orange)and using the Coulomb potential (blue) (c),(f),and (i).

Statistical properties of non-interacting electron gas in NPLs

A single electron state can simulate the statistical behavior of a system with many electrons.Here,we want to emphasize again that the NPL is discussed within the framework of weekly interacting electron gas when the number of electrons is much less than the number of impurities.To determine the thermodynamic properties of the system,one must calculate its partition function,which involves summing over all the possible states of the system.The partition function can be expressed using the following equation,under the assumption that the electron gas follows Boltzmann statistics [34,35]:

whereβ=1/kTis proportional to the inverse temperature,andνis the set of the quantum numbers.Numerical calculations are performed to determine the sum in the partition function.The number of states to be considered is obtained by examining the dependence of the partition function on the number of states,as shown in a previous study [26,36].For each case,we identify the number of states that need to be considered,after which the values of the partition function do not vary significantly.The thermodynamic parameters,such as the mean energy,free energy,mean heat capacity,and entropy,can be calculated using the following expressions:

The mean heat capacity and entropy can also be calculated using the partition function:

The thermodynamic properties are summarized in figure 4.

Based on the results obtained above,it is possible to determine the thermodynamic characteristics of an ideal electron gas localized in a multi-impurity system with random impurity locations.Figure 4 shows that the mean energy increases with temperature,displaying a linear dependence at small temperatures and a nonlinear dependence at higher temperatures (the slope changes and curves reach a plateau).This is a reflection of the fact that,with an increase in temperature,due to the transfer of thermal energy to the electrons,low energy levels begin to be filled.There is not enough thermal energy for further particle transition to higher energy levels(see figures 3(b),(e),and(h)).This explains the plateau of the mean energy curve.Such behavior of the antiderivative (mean energy) leads to the corresponding behavior of its derivative.Due to the saturation factor,the heat capacity of the system is different from zero only for the region of low temperatures (see figure 4(b)).The peaks of specific heat curves lie in the range of low temperatures.For smaller numbers of impurities,the width of the peak becomes narrower and higher.This is because the occupation probability of the levels changes with the temperature rising and the mean energy value monotonically increasing,demonstrating nonlinear behavior at sufficiently high temperatures.Similar behavior has been reported in [26,27].

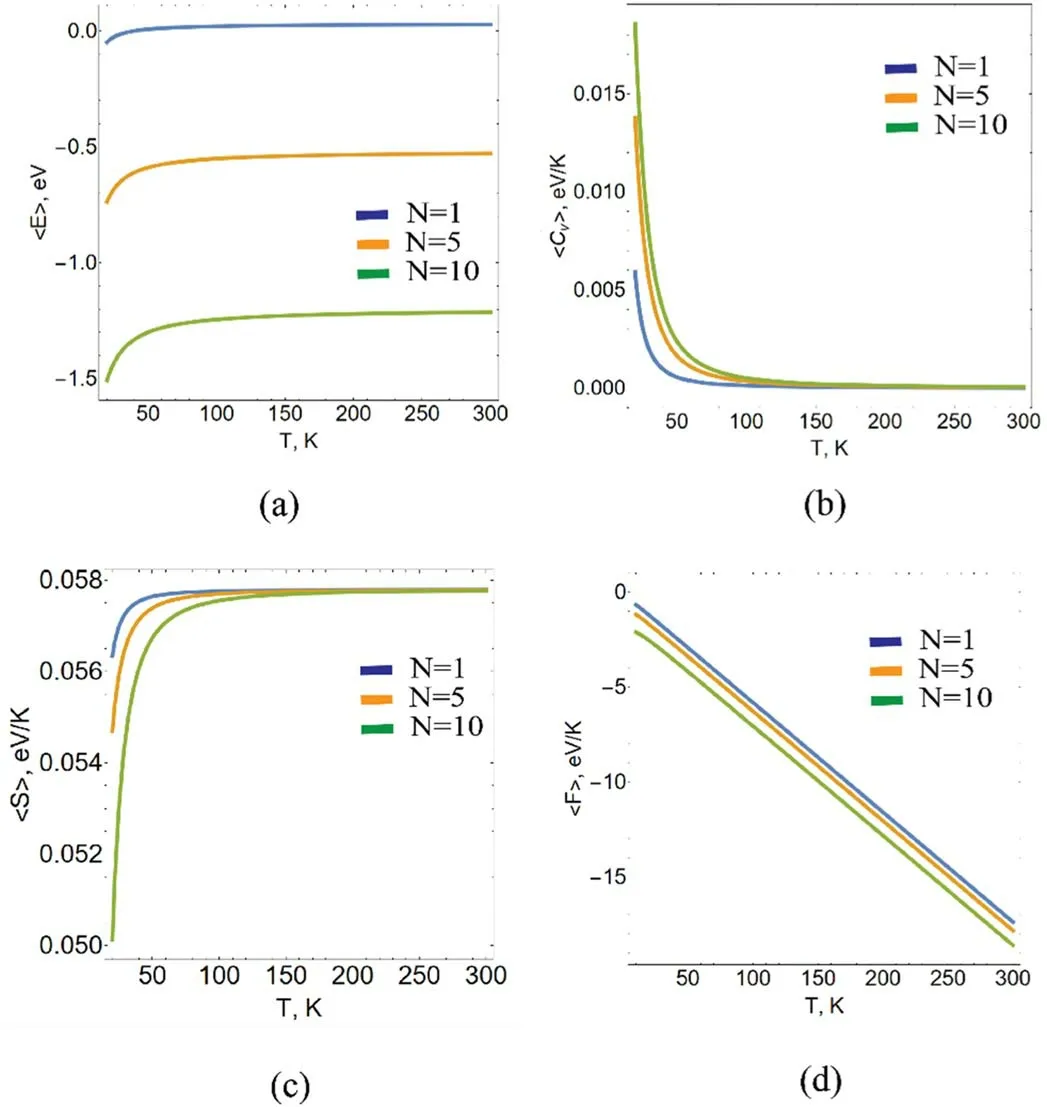
Figure 4.(a) The mean energy dependence on temperature for different numbers of impurities N in NPLs.(b) The dependence of heat capacity on the temperature.(c) The entropy dependence on temperature for different numbers of impurities per NPL.(d) The free energy dependence on temperature.All curves were calculated for n=3 and random impurity locations.

As one can see in figure 4(c),the entropy is monotonically increasing with the increase in the temperature,reaching a constant value,independent of the number of impurities.The nature of the electron spectrum of the system under consideration also regulates the behavior of entropy with temperature.With the temperature increase,the occupation probability of the closer to the ground energy levels increases and,thereby,the system disorder increases.However,with a further increase in the temperature,the impossibility of filling the higher levels,in this case,will result in the appearance of a plateau in the temperature dependence of the entropy curve.As seen in figure 4(c),at a fixed temperature regime,the slope of the entropy dependence curve decreases with the increasing number of impurities.This is still explained by the fact that an increase in the number of impurities increases the number of nearby levels,as a result of which,entropy depletion occurs at higher temperatures.With regard to the behavior of another thermodynamic potential—free energy—in the considered temperature regime it decreases linearly with increasing temperature (figure 4(d)).This can be explained by the already noted above circumstance that with increasing temperature,the average energy and entropy of the system remain practically unchanged,leading to lowering of the free energy.

Conclusion

We have theoretically studied the multiple impurity effects in NPLs and thermodynamic properties as a function of many impurities and temperature.The effect of dielectric confinement on the one-electron energy spectrum and wave functions is studied.It has been shown that the consideration of polarization effects makes the electron–impurity potential stronger and more long-range;this makes the potential of multiple impurities also much stronger.It has been demonstrated that the binding energy increases for a larger number of impurities.The energies of the electron and corresponding wave functions in the NPL plane have been calculated.The thermodynamic properties of the non-interacting electron gas have been calculated using the partition function.The mean energy increases monotonically,with the temperature increase reaching a plateau.The heat capacity increases until it reaches the maximum and then reduces with increasing temperature.With the temperature increase,the entropy increases monotonically until they reach one specific value.

Acknowledgments

The work was funded by the RA Science Committee as part of a ‘Leading scientific research support program’ within the framework of research project 21AG-1C022.

Author contributions

HAS,VAH,DAB and EMK,conceptualization and development of the theory;DAB,numerical calculations;DAB,HAS,original draft preparation;HAS,VAH,EMK,review and editing.

All authors have read and agreed to the published version of the manuscript.

Conflict of interests

All authors have no conflicts of interest.