Zhouqing Tang(唐周青), Shaobo He(賀少波), Huihai Wang(王會(huì)海),?, Kehui Sun(孫克輝),Zhao Yao(姚昭), and Xianming Wu(吳先明)

1School of Electronic Information,Central South University,Changsha 410083,China

2School of Automation and Electronic Information,Xiangtan University,Xiangtan 411105,China

3School of Physics,Central South University,Changsha 410083,China

4School of Mechanical and Electrical Engineering,Guizhou Normal University,Guiyang 550025,China

Keywords: chaos,fractional difference,variable order,multistability,complexity

1.Introduction

It is well known that chaotic systems are generally classified into two categories according to their continuity in time domain: the continuous systems and the chaotic maps.Among them, the chaotic maps gradually become a hot research topic due to easy implementation, low cost and high complexity.In addition,they have broad application prospects in cryptography,[1,2]image encryption,[3,4]pseudorandom sequences generation,[5,6]secure communication[7,8]and other fields.[9-11]However, many existing chaotic maps still have limitations such as small keyspace,multiple periodic windows and weak ergodicity.[12]Therefore, it is necessary to design the enhanced discrete chaotic systems to resist these disadvantages.

The introduction of fractional order is a new approach to achieving enhanced chaotic systems effectively.Although the theory of fractional calculus is more than 300 years old,it still develops slowly due to the lack of practical application background.The study is still in infancy to combine it with discrete chaotic systems to construct fractional-order(FO) difference models.Meanwhile, research on FO chaotic systems is mainly focused on the continuous domain and there are many chaotic systems investigated such as fractional Chua’s system,[13]fractional Jerk system[14]and fractional Chen system.[15]Up to now, many definitions of the fractional operator have been proposed and studied,mainly including Riemann-Liouville definition,[16]Caputo definition[17,18]and Grunwald-Letnokov definition.[19]Among them,Caputo definition has received the most attention because of easy implementation in engineering,and many publications in recent years[20-22]show that this definition can also be combined with difference equations to form chaotic maps.Tarasovet al.[20]derived the fractional standard map from the fractional differential equations of a kicked system, and pointed out its main property was a long-term memory.Edelman[21]extended the definition of fractional maps to include all positive orders and investigated their complex behaviors using fractional logistic map as an example.Liet al.[22]proposed a fractional sine chaotification model based on the theory of discrete fractional calculus and applied it to image encryption.Due to the existence of memory effect,[23]the FO difference has great advantages in describing systems with nonlinear characteristics,and the dynamic behaviors of the enhanced systems with fractional order can be more complex.

Most of the existing researches on FO systems focus on the operators with a fixed order.The order is treated as a special parameter, and different fractional orders can enrich the dynamic behaviors of the system.[24]Generally, researchers evaluate the effect of different orders on the system performance, and then select the best case for application analysis.In fact,the fixed order is a special case in the real world.Because of some external interference,the order usually changes over time during the evolution of systems.[25]Therefore,considering the physical properties and memory characteristics of objects under certain conditions, the variable order is more suitable for models that describe the nonlinear change of physical quantities such as neuronal system and field energy.[26,27]Some related works for description or prediction have been carried out in different engineering fields.Zhanget al.[28]proposed a time variable FO advection-dispersion model to describe anomalous diffusion, and discussed the stability and convergence of its implicit Euler approximation.Yanget al.[29]developed a new variable-order fractional model which applied to the transport process in the inhomogeneous media.Meanwhile, some researchers have successfully introduced variable order into discrete fractional chaotic systems and achieved satisfactory application results.Wuet al.[30]assigned different values to the order of fractional logistic map piecewise,and applied the map to fast image encryption.Huanget al.[31]investigated the short memory and variableorder fractional neural networks based on the stability conditions.

Fractional models with variable order have shown potential application value in many fields.However,most publications of the variable-order fractional discrete systems focus on the mathematical properties such as the approximation, fixed point and boundary conditions,while the dynamical behaviors of the systems such as bifurcations and chaos are rarely investigated.Inspired by the above,we wonder whether the introduction of variable order can overcome the mentioned limitations of existing discrete chaotic systems.Thus, a novel variable-order fractional chaotic map is proposed, in which the order also participates in the iteration and is related to the current state of the system.We believe the order should not be treated as an isolated variable but changes with the system state,so that the complex nonlinear systems may be better described.Then we focus on the numerical simulations to verify that the variable order can enrich the dynamic behaviors of the system and improve the chaotic performance.

The rest of the paper is organized as follows.Section 2 presents the fractional difference of Caputo-like sense and the numerical solution.In Section 3, we give the introduction of fractional sine map (FSM) and the design of a new variableorder fractional sine map(VFSM)followed by the discussion of fixed point and stability.Section 4 analyzes the dynamics of the proposed maps by phase diagrams,time sequences,coexisting attractors, bifurcations, Lyapunov exponents and complexity.Section 5 discusses the applications of VFSM with parameter estimation and statistical test for pseudorandom number.Finally, we conclude the paper and discuss the future work.

2.Preliminaries

Then-order forward difference of fractional calculus is defined as

Equation (7) is the numerical solution based on the FO difference operator, and the equation degenerates to the integerorder form whenv=1.It should be noted that the fractional difference equations do not have periodic solutions except period one(fixed point).[37,38]

3.Design of the variable-order fractional sine map

3.1.Definition of the FSM

As the most basic and common model, the sine function has been used widely in the construction of various chaotic systems.The classical discrete sine chaotification map[39]is expressed as

In a fractional discrete system,the falling factorial assigns special forms of weights to each iteration.These forms are represented by combinations of gamma functions.The present state evolution of the map depends on the sum of all past states,which is the reflection of the memory effect.[20]

3.2.Presentation of the new VFSM

Based on the above,we replacevwith a variable functionv(n),[40]and obtain

wherev(n)∈(0,1]is the variable order.The existence of variable orderv(n) can change the weight factors to affect the iterative process ofx(n).In Ref.[30],v(n) is defined as a piecewise constant function, which is proved to be an effective modeling method to enrich chaotic dynamics as well as enhance the nonlinearity of the system.

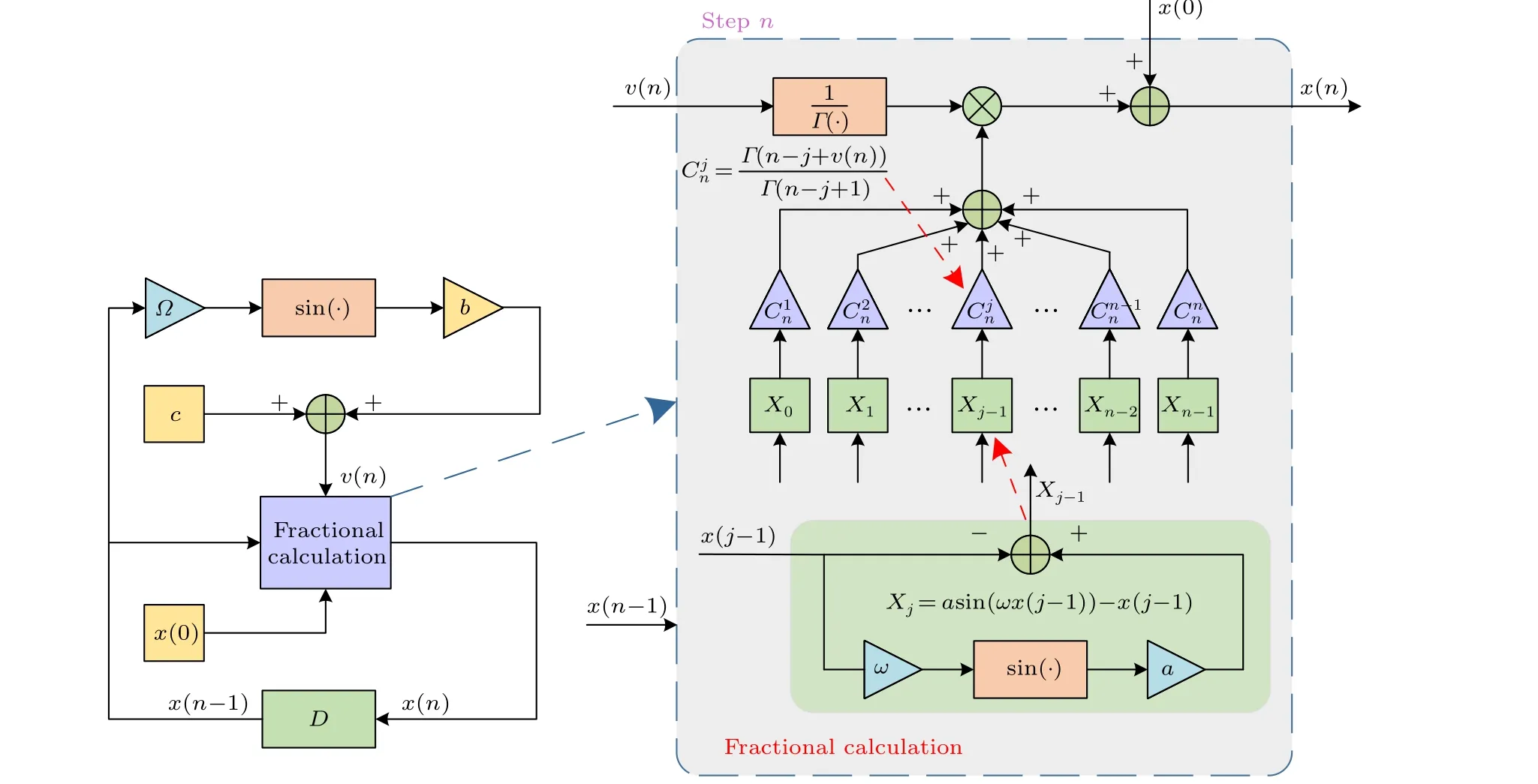
Fig.1.Block diagram of the VFSM.

From the perspective of engineering,the time-varying orderv(n)can describe the change process of nonlinear physical quantities more precisely comparing to the piecewise constant functionv(n) in fractional systems.Considering the requirement of 0＜v ＜1 in Theorm 1(ifv=1,the numerical solution Eq.(7)is equivalent to the integer-order form),the sine function whose range fluctuates in a finite interval [-b+c,b+c]is selected as

where the coefficientsbandcsatisfy the conditions-b+c ＞0 andb+c ≤1,andΩis the parameter.

In practical problems, the order is supposed to be influenced by the state of the system in some way, rather than changing independently.Therefore,we replacenbyx(n-1)on the right-hand side of Eq.(12), so that the variable order also participates in the evolution with the last state of the system.Thus the final equations of the new variable-order fractional sine map(VFSM)are

wherex(0)is the initial value,aandωare the system parameters,andΩis the variable-order parameter.For the sake of intuitive understanding,we draw the block diagram of VFSM in Fig.1,whereDis the unit delay.In the fractional calculation module, due to the long-term memory effect, the calculative amount will continue to increase as the iteration runs.

3.3.Fixed points and stability

Due to the particularity of FO systems, fixed points are usually solved approximately by the corresponding integerorder ones.For the proposed VFSM,the fixed points are calculated as

The stability of a fixed point can be reflected by the gradient of the system at that point.[39]And the fixed point is stable if the corresponding gradient value is within[-1,1],otherwise it is unstable.For the VFSM,since it can be equivalent to a onedimensional system, the gradient of the system is calculated by the derivative

Obviously, in the first case of Eq.(15),λ=aω ≤1, so the only fixed pointx*=0 is stable.While for the case ofaω ＞1,the fixed pointx*=0 is unstable, and the system can have multiple attractors.Suppose thata=3 andω=π,we can get all the 7 fixed points by numerical calculation,which are listed in Table 1.The results show that all fixed points are unstable,implying the multistable behaviors of the proposed system.

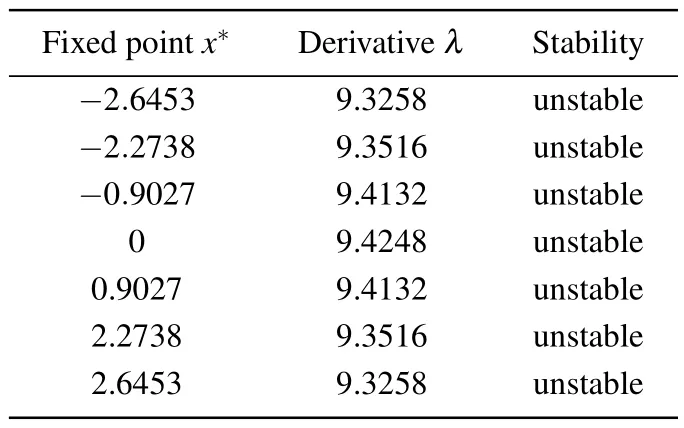
Table 1.Fixed points and stability analysis.

4.Dynamics of the VFSM

In this section,we analyze the dynamical behaviors of the proposed VFSM by numerical simulations, including phase diagram,coexisting attractors,bifurcation and complexity.For comparison,FSM with fixed orderv=0.95 is selected for the same analysis.

4.1.Phase diagram and time sequence

We setx(0)=0.1 and the parameters asω=πandΩ=1000.Specially, for VFSM we discuss the casesb=0.249,c=0.25;b=0.499,c=0.5 andb=0.25,c=0.75 to keep the range ofv(n) between [0.001,0.499], [0.001,0.999] and[0.5,1]respectively.With the number of iterationsN=20000,the phase diagrams with different parameters are shown in Fig.2.

Fig.2.Phase diagrams of(a)FSM with a=1.5,(b)VFSM with(a,b,c)=(1.5,0.249,0.25),(c)VFSM with(a,b,c)=(1.5,0.499,0.5),(d)VFSM with(a,b,c)=(1.5,0.25,0.75),(e)FSM with a=3,(f)VFSM with(a,b,c)=(3,0.249,0.25),(g)VFSM with(a,b,c)=(3,0.499,0.5),(h)VFSM with(a,b,c)=(3,0.25,0.75).

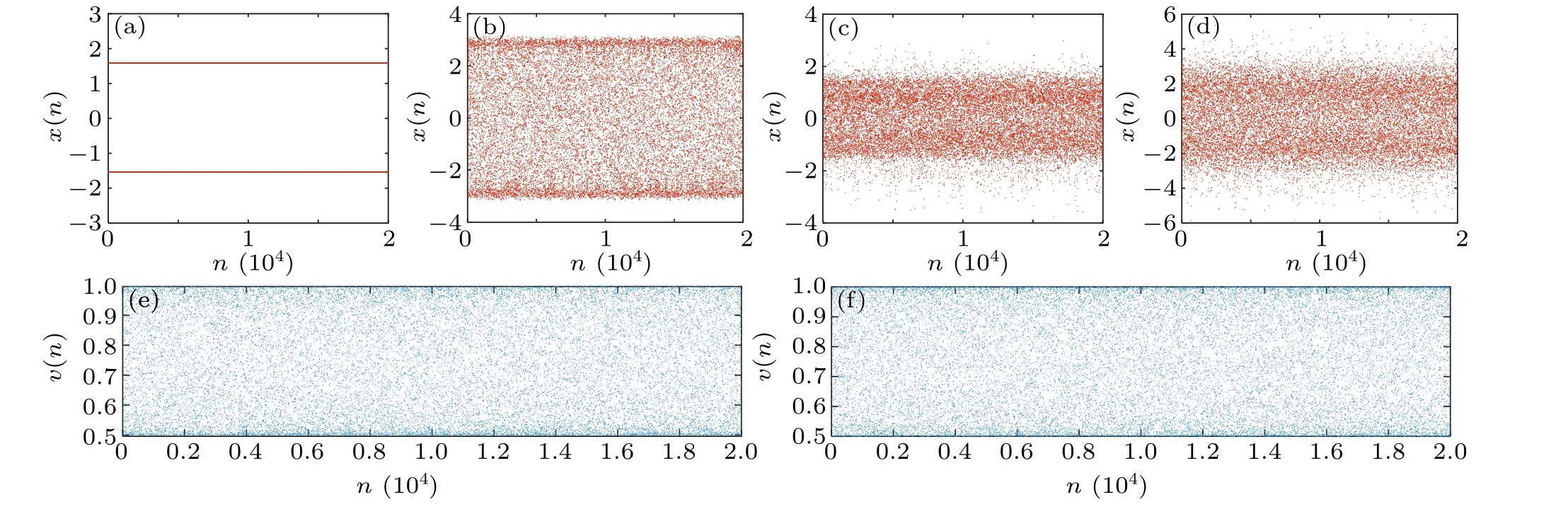
Fig.3.Time sequences of(a)FSM with a=1.5,(b)FSM with a=3,(c)VFSM with a=1.5,(d)VFSM with a=3,(e)v(n)with a=1.5,(f)v(n)with a=3.

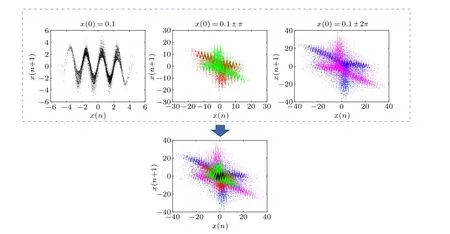
Fig.4.Coexisting attractors of the VFSM.

Whena=1.5, FSM shows only two independent points(-1.54328,1.59299) and (1.59299,-1.54328) in Fig.2(a).Whena= 3, the phase diagram shows a clear sine-wave in Fig.2(e), which reveals that FSM enters a chaotic state.While for the cases of VFSM, Figs.2(b)-2(d) whena=1.5 and Figs.2(f)-2(h) whena= 3 all show sinusoidal waves that spread around,which indicates more obvious chaos compared with FSM under the same conditions.Besides,different ranges ofv(n) can also change the distribution of the phase diagrams.The sinusoidal waves whenv(n)∈[0.001,0.499](Figs.2(b)and 2(f))andv(n)∈[0.001,0.999](Figs.2(c)and 2(g)) are deformed and concentrated aroundx(n+1) = 0,which may attenuate the randomness of the system.Therefore, to get the more uniform and more sinusoidal phase diagrams,we fixb=0.25 andc=0.75 in the later analysis.The corresponding time sequences are shown in Fig.3.

In Fig.3(a), the time sequence of FSM shows two lines aroundx(n)=-1.54328 andx(n)=1.59299 whena=1.5,which corresponds to Fig.2(a).Whena=3, it can be seen from Fig.3(b)that FSM is chaotic,but the boundaries of phase points are clear at-3 and 3.While for the cases of VFSM,both time sequences in Figs.3(c)and 3(d)are distributed more uniformly in the range around[-a,a].Comparing with FSM,the chaotic characteristics of VFSM are obviously enhanced.Besides, Figs.3(e) and 3(f) show the time sequences of variable order in VFSM ata=1.5 anda=3 respectively.It can be seen that the values ofv(n)are fully mapped within[0.5,1],proving that the variable order changes over time with good randomness.

4.2.Coexisting attractors

Chaotic systems are sensitive to initial values.Given different initial values for centain parameters, the system may produce different trajectories and eventually form several different attractors called coexisting attractors.[41]When we set different initial valuesx(0) for VFSM with fixed parameters(a,b,c,ω,Ω) = (3,0.25,0.75,π,1000) andN= 20000, the phenomenon of coexisting attractors appears in the simulation as shown in Fig.4.

The black attractor is a regular planar sinusoidal waveform with blurred edges whenx(0)=0.1.While the initial value turns to 0.1±π, the red and green attractors become two triangular star topologies that are symmetric about the origin.Similarly, blue and magenta ones are a pair of attractors symmetric about the origin when the initial value is 0.1±2π.Compared to the previous pair, they have the same structure but larger area.As a supplement, the corresponding information is listed in Table 2.We can see that all five attractors are chaotic with different initial values.Moreover, whenx(0)continues to increase in both directions,the attractor pairs will also expand to a larger plane with the same triangular star structure.Therefore,VFSM has countless pairs of coexisting attractors reflecting the extremely multistable behavior, and the cryptosystems based on this chaotic system are generally considered to be more secure than others.

Table 2.The states of VFSM with coexisting attractors.

4.3.Bifurcations and Lyapunov exponents

Bifurcation is the dynamic evolution process of a chaotic system with parameters.Lyapunov exponent(LE)can quantitatively characterize the state of systems.For one-dimensional discrete systems, a positive LE value implies chaos.Therefore, the bifurcation diagram and LE spectrum are generally combined to assess the state of chaotic systems.Here,we use the wolf algorithm[42]based on the generated sequence to calculate LE.Firstly,with the parametersω=π,Ω=1000,the number of iterationN=5000 and the step sizeh=0.01, we plot the bifurcation diagrams and LE spectrums varying withain Fig.5.

The bifurcation diagram in Fig.5(a)is interspersed with white space, and the corresponding LE spectrum parts are below the zero line.It is clear that FSM does not become chaotic untila=0.81,and there are several non-chaotic windows during the evolution,which result in sharp fluctuation of the LE values.While for the case of VFSM,Fig.5(b)shows a global chaotic state with stable positive LE values throughouta ∈[0,5].The non-chaotic windows disappear,which can provide more available values for chaotic parameters.Moreover, the bifurcation diagram distributes more uniformly, and it brings more randomness to the system.

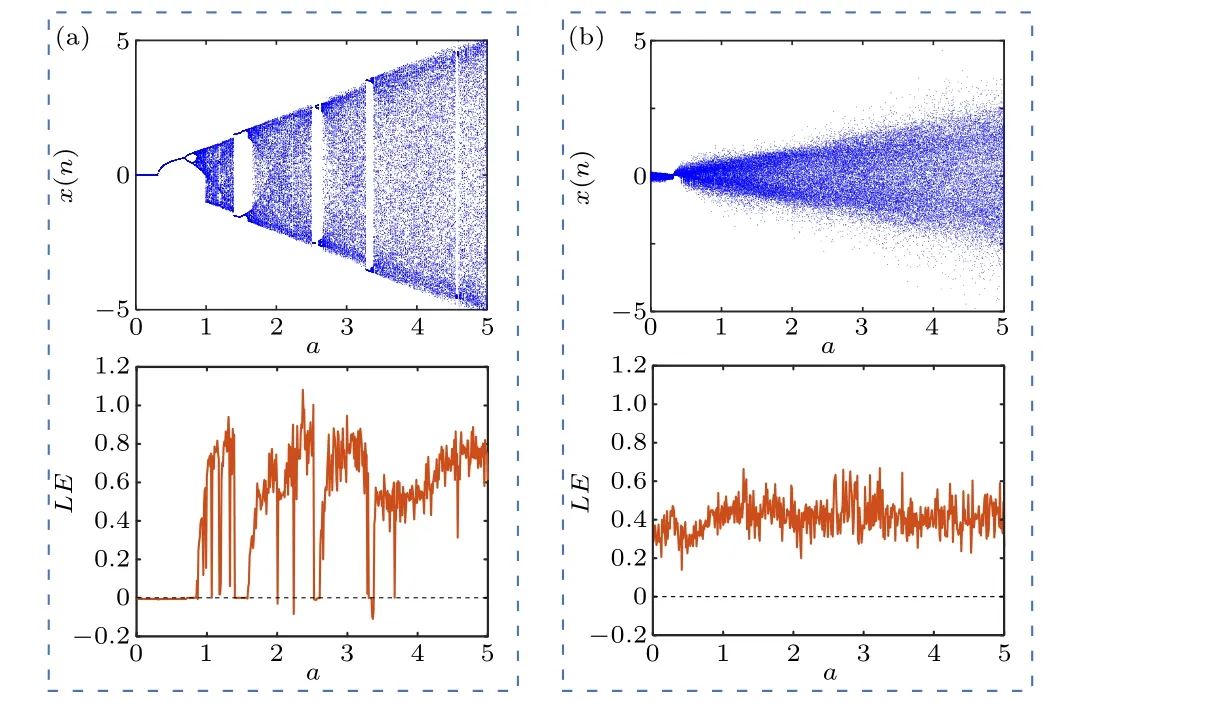
Fig.5.Bifurcation diagrams and LE spectrums varying with a.(a)FSM(ω =π),(b)VFSM(ω =π,Ω =1000).

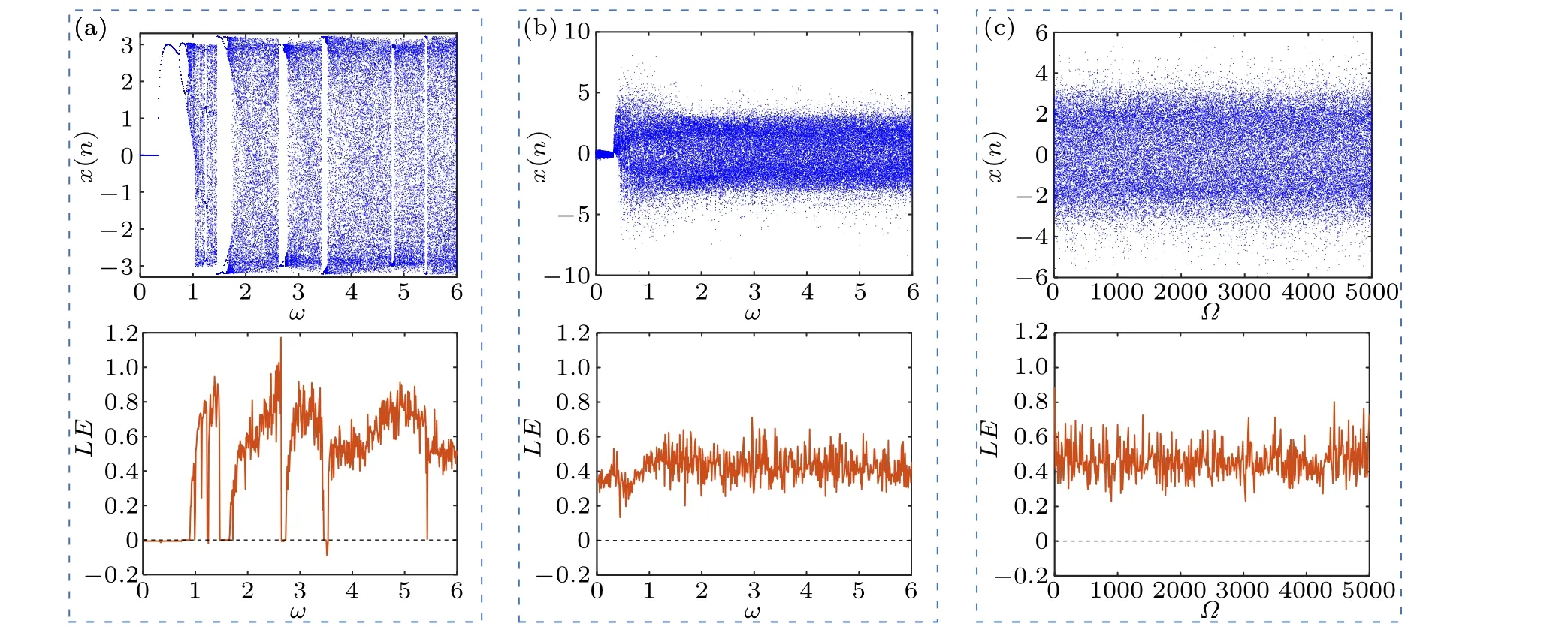
Fig.6.Bifurcation diagrams and LE spectrums when a=3.(a)FSM varying with ω,(b)VFSM varying with ω (Ω =1000),(c)VFSM varying with Ω (ω =π).

Then,we plot the bifurcation diagrams and LE spectrums varying withωandΩof FSM and VFSM respectively in Fig.6.Similarly,as the parameterωincreases from 0 to 6 in Fig.6(a),some values also cause FSM to enter a non-chaotic state.In contrast, VFSM can reach the chaotic state earlier,and does not return to non-chaotic as the parameterωcontinues to grow in Fig.6(b).Through the analyses of above,it is found that VFSM can effectively reduce the non-chaotic windows, and achieve global chaos with positive LE stably.In addition,the parameterΩofv(n)shows little influence on the VFSM state in Fig.6(c),but the system can still maintain chaotic over a large area.

4.4.Complexity

The complexity is an index to measure the randomness of sequence generated by a chaotic system.Generally, the more random the sequence,the greater the value of complexity,and the higher security of the applied cryptosystem.Here we choose the fuzzy entropy (FuzzyEn) complexity[43]with good robustness and high differentiation to evaluate FSM and VFSM.The results of chaos diagrams are presented in Figs.7 and 8 with the number of iterationN=10000 and the step sizeh=0.01.

For the common parametersaandω,it can be seen from Fig.7 that FSM and VFSM differ little in maximum complexity index, which is 3 and 3.5 respectively.However, in Fig.7(a) the chaos diagram of FSM shows several blue diverging areas in the wholea-ωplane.What’s worse,the complexity indexes of FSM are almost 0 when the parameteraorωtakes a small value,and it brings great security risks to the practical application.While for the case of VFSM in Fig.7(b),the blue diverging stripes disappear obviously, and the proportion of low complexity region is significantly reduced for small values of the parameters.The comparison result proves that the variable order can effectively improve the complexity of FSM, bring more choices of parameter values and enhance practicability in engineering.Besides, Fig.8 shows a uniformly layered color graph withavariation,indicating that the parameterΩhas little effect on the complexity of VFSM.

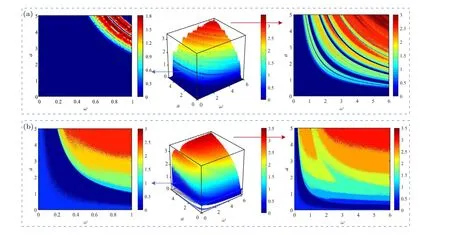
Fig.7.Chaos diagrams based on FuzzyEn in the a-ω plane.(a)FSM,(b)VFSM.

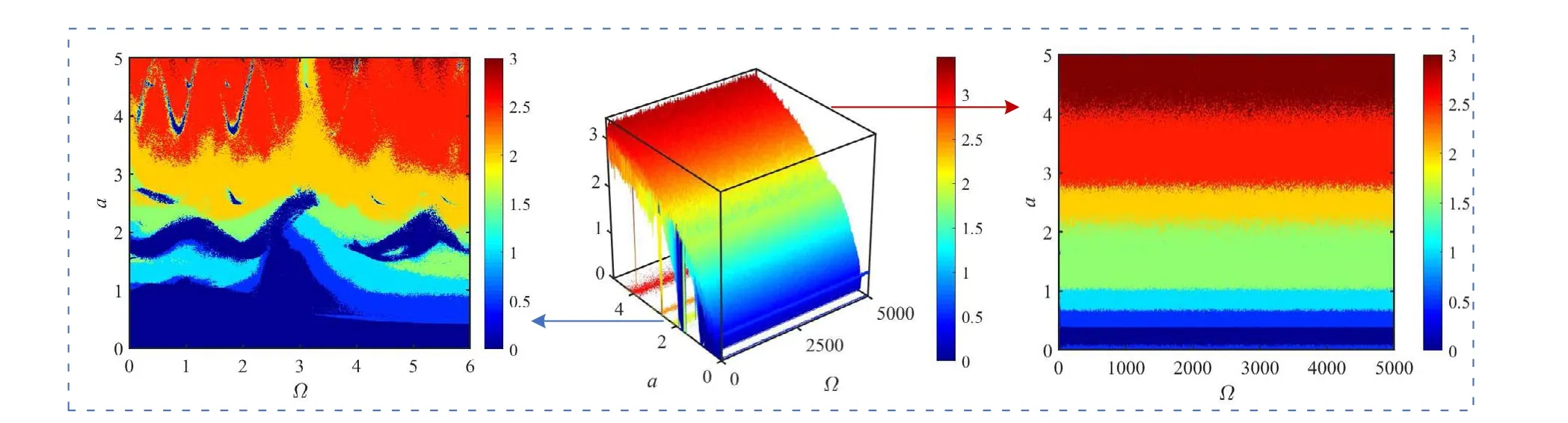
Fig.8.Chaos diagrams based on FuzzyEn of VFSM in the a-Ω plane.

We further compare the FuzzyEn complexity trends of sine map, FSM and VFSM when the common parameteravaries within a large range [0,100].Under the same initial value condition, the comparison results are shown in Fig.9 with the number of iterationN= 10000 and the step sizeh=0.03.The green curve is higher than the other two at the beginning, indicating that the complexity index of VFSM is the largest whena ∈[0,20].Asacontinues to increase,all the three curves fluctuate at a height of about 5.5.VFSM has two obvious peaks whena=68 and 79.3, and the corresponding complexity values reach 8.7 and 8.9 respectively.Therefore,VFSM can appropriately improve the FuzzyEn complexity in case the parameter takes a small value,while the proper selections ofa(at the peaks)can even have a remarkable effect.

Fig.9.FuzzyEn complexity of sine map,FSM and VFSM.

To comprehensively analyze the performance and effectiveness of VFSM proposed in this paper,we then select some typical chaotic maps to compare the FuzzyEn complexity,including IPM,[44]FO logistic map,[45]cycloid map,[46]folded towel map,[47]and 3-NHM map.[48]For convenience, we choose only one parameter of each system varying in[0,100].The selected parameters and final equations of all maps are listed in Table 3.From Fig.10, we can find that the folded towel map and FO logistic map perform very poorly in the complexity of the FuzzyEn algorithm, even less than 1.The performance of 3-NHM is not much better,whose curve fluctuates at first and is finally stable around a height of 1.8.Cycloid map and IPM map can reach high complexity (around 5.5),but there are some downward spikes in the evolution that bring instability.By contrast,VFSM can maintain high complexity when the parameter takes small values, and the complexity steadily increases(with two obvious upward spikes)as the parameter value increases, which proves that it can effectively generate sequences with better randomness and higher security.

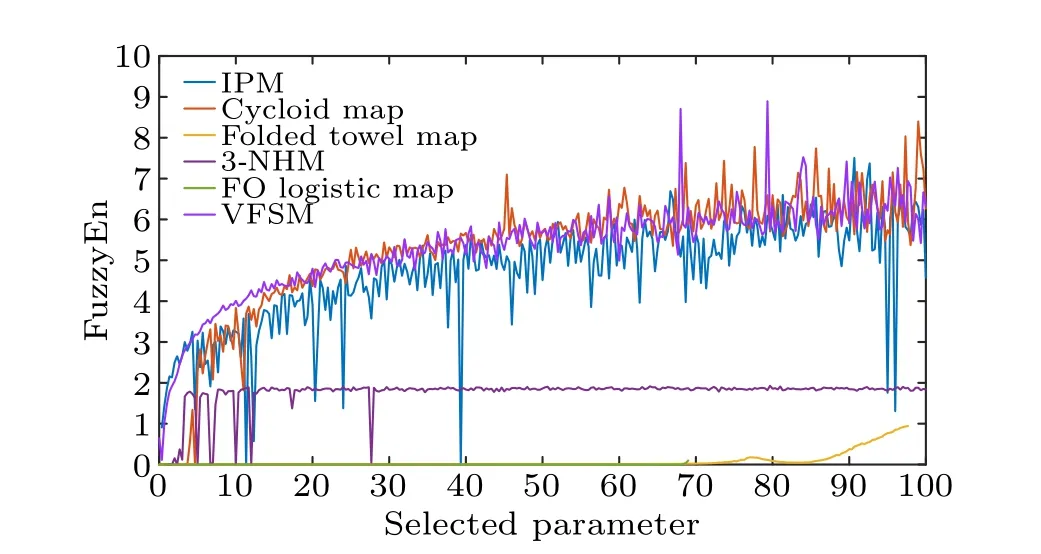
Fig.10.FuzzyEn complexity of different chaotic maps.

Table 3.Information of the chaotic maps for comparison of FuzzyEn complexity.

5.Application analysis

5.1.Parameter estimation test

Parameter estimation test is a method to speculate the unknown parameters through the sequences generated by a certain system.If the parameters of a chaotic system are easy to estimate successfully,there will be security risks when it is applied to communication.The return map(RM)algorithm[49]is proposed to estimate system parameters based on the similarity between the estimated sequence and the original sequence.On this basis,to make up for its shortcoming in local search capability,we use the improved return map(IRM)algorithm.[50]

Figure 11 shows the flow chart of the IRM algorithm,wheregis the differential evolution algorithm generator.Gis the maximum number of iterations, andPbis the current optimal parameter,andGbis the global optimal parameter.The objective functionJis expressed as

whereMis the length of the sequence,Xtis the original sequence,and ?Xtis the estimated sequence.The IRM algorithm combines the differential evolution algorithm with the RM algorithm,and avoids the impact of initial value sensitivity.

We apply the IRM algorithm to the VFSM,and compare the parameter estimation results with sine map, FSM, IPM,cycloid map,folded towel map,3-NHM and FO logistic map.After 1000 iterations,each system retains the last 300 data as the original sequence for parameter estimation.Then we take every ten estimation results as a group,and record ten groups continuously (100 estimation results in total).For each estimate result,the criteria for pass is to find the exact parameter values.The higher the pass rate, or the shorter the running time of estimation,the easier it is to hack the system,and the corresponding security risk is also higher.To obtain a fairer comparison of results,we discard the groups with the highest and lowest pass rates of each system, and take both the pass rate and the average run time as the rank standard.

Table 4 shows that VFSM has the lowest pass rate and the longest running time of estimation,so it ranks first among the eight typical systems.The comparison results prove that it is difficult to speculate the accurate parameters through the generated sequences by VFSM.Therefore, the cryptosystem based on VFSM will have higher security.

Fig.11.Flowchart of the IRM algorithm.

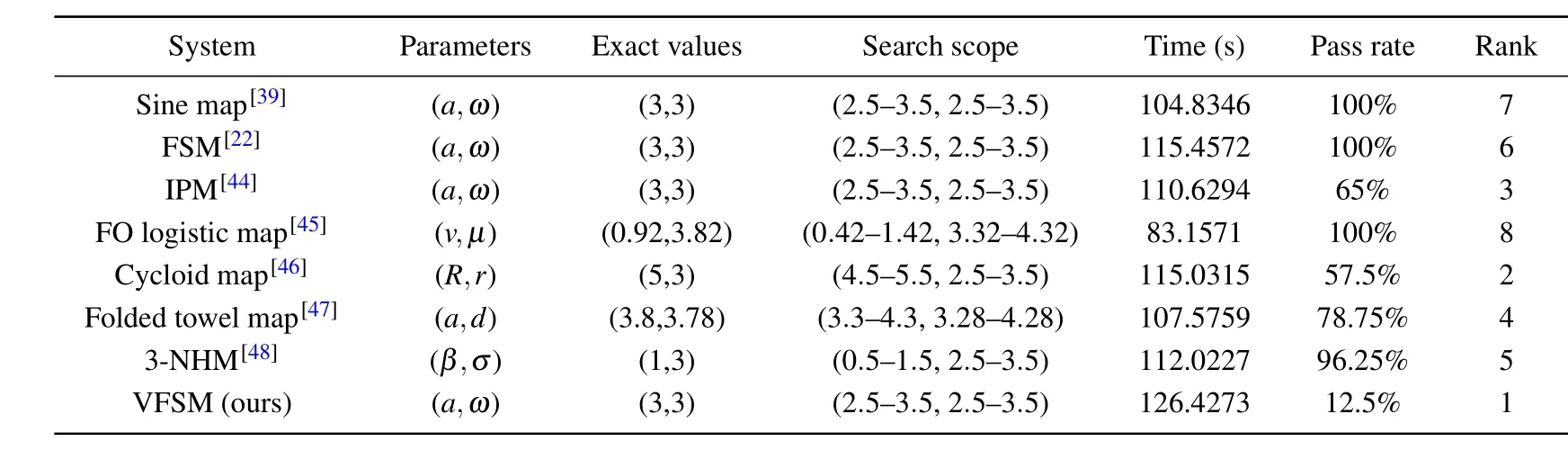
Table 4.Parameter estimation results of IRM algorithm.

5.2.NIST test

The statistical test suite of the National Institute of Standards and Technology (NIST) is an effective method to evaluate the randomness and security performance of pseudorandom number generators.It includes 15 indicators,and the test results of each indicator are measured by the pass rate andP-value.Before testing, the sequences generated by the proposed chaotic map should be quantized into binary sequences.We select the binary quantization algorithm with high iteration utilization[51]and inputxigenerated by VFSM.The quantization formula is

AfterNiterations, the quantized 0-1 sequence with a length of 8Ncan be obtained.And then we conduct the NIST test on the pseudorandom number sequence to evaluate the randomness.The requirements for a group of sequences to pass the test are as follows.

(i)TheP-value is larger than 0.0001.Besides,the largerP-value,the better randomness.

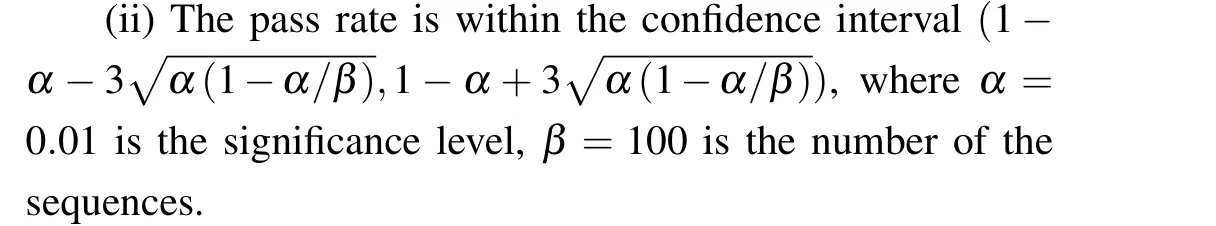
In the case ofa= 3,b= 0.25,c= 0.75,ω=π, andΩ=1000, the NIST test results of VFSM are shown in Table 5.For indexes with multiple tests, the lowestP-values and proportions are presented as the final results.It can be found that all theP-values in 15 test indexes are much greater than 0.0001, and the proportions of the pass rate within the confidence interval are almost always 100%.Therefore, the generated pseudorandom sequence has successfully passed the NIST test, which indicates that VFSM has good randomness and high credibility for application.

Table 5.NIST test results.

6.Conclusion

A novel variable-order fractional sine map is proposed based on the Caputo-like fractional difference.The dynamical properties of the map are studied in terms of phase diagrams, time sequences, bifurcation diagrams, LE spectrums and FuzzyEn complexity.The comparison results between FSM and VFSM show that the introduction of variable order can not only reduce the non-chaotic windows effectively, but also enhance the chaotic characteristics.Besides, the multistable phenomenon is found with infinite pairs of coexisting attractors,indicating VFSM is very sensitive to the initial values.Moreover, the proposed chaotic map can resist the parameter estimation well,and the generated pseudorandom sequences also pass the NIST test successfully, which shows a good application prospect on the information security.Variable order provides a new direction for the study of discrete FO models,and we can keep exploring more forms of variable order, analyzing the influence on high-dimensional systems,or focusing on the applications,such as image encryption and memristors in the future work.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.62071496, 61901530, and 62061008) and the Natural Science Foundation of Hunan Province of China(Grant No.2020JJ5767).