Phase diagram of muonium hydride: the significant effect of dimensionality
Jieru Hu and Massimo Boninsegni
Department of Physics,University of Alberta,Edmonton,Alberta T6G 2H5,Canada
Abstract We carry out a theoretical investigation of the low-temperature phase diagram of muonium hydride in two dimensions,using numerical simulations.It is shown that the phase diagram of this substance is qualitatively different in two and three dimensions.Specifically,while in three dimensions it is essentially identical to that of parahydrogen,i.e.,only displaying a single(crystalline)phase.In two dimensions it is very similar to that of 4He,with an equilibrium liquid phase that turns superfluid at a temperature as high as ~2.2 K,and crystallizes under applied pressure.This is a well-described case of a continuous-space condensed matter system whose ground state equilibrium phase is qualitatively altered by dimensional reduction.
Keywords: quantum fluids and solids,quantum Monte Carlo,phase diagrams
1.Introduction
One of the most important tenets of modern condensed matter theory,is that thermodynamic properties of macroscopic assemblies of particles are strongly affected by dimensionality.Far-reaching fundamental statements can be made about the thermodynamics of condensed matter systems in reduced dimensions,such as that no true long-range order can exist at any finite temperature (e.g.,no Bose–Einstein condensation can take place).Moreover,phase changes like melting at finite temperature,featuring intermediate hexatic phases[1–3],or the superfluid transition [4],are amenable to very different theoretical descriptions,depending on whether they occur in three or two physical dimensions;in one dimension(1D),the very notion of phase transition becomes blurred.Furthermore,there exist remarkable physical phenomena that only occur if particle motion is restricted to fewer than three dimensions(3D).One may think of the Quantum Hall Effect,which owes its very existence to the confinement of electrons to two dimensions (2D).
The observation of possible,novel behavior of condensed matter systems in which particle motion is confined to 2D or 1D has motivated much experimental research over thepast few decades.This includes,for example,the study of atomically thin films of helium adsorbed on different substrates,or in the essentially one-dimensional confines of carbon nanotubes.Lowering the dimensionality (e.g.,from three to two),with the ensuing reduction in the magnitude of the potential energy of interaction among particles(due to the smaller coordination number),was also speculated to bring about important qualitative changes in the phase diagram of a substance,with respect to what is observed in 3D.This was especially thought to be the case for highly quantal fluids,such as helium or parahydrogen.An important possible consequence,in the case of parahydrogen,may be the stabilization of a liquid phase,turning superfluid at a low temperature [5],whose occurrence is preempted by crystallization in 3D (no supersolid or metastable superfluid phases exist) [6].
If the interactions among particles are anisotropic (e.g.,dipolar),then the phase diagrams in 2D and 3D can differ significantly [7].However,reliable theoretical studies have shown that aside from well-understood,mainly formal(in this context) modifications to the theory brought about by dimensional reduction,the phase diagram in 2D of systems with central,pair-wise interactions remains qualitatively the same as in 3D.For Lennard–Jones type systems such as helium,the basic features of the phase diagram are determined by the value of a dimensionless parameter of the form Λ ≡?2/(m?σ2),where m is the mass of the particles,while ?and σ are,respectively,the depth of the attractive well and the diameter of the repulsive core at short distances of the pair potential [8].
To mention a few examples among systems for which quantum-mechanical effects are most significant,the phase diagram of the electron gas is qualitatively the same in 2D and 3D [9,10].The same is true of4He,which in 2D has an equilibrium superfluid phase at low temperature,which crystallizes under pressure[11];the main features of the same phase diagram,and in particular the equilibrium phase,are the same.The same observation can be made for parahydrogen,only displaying a crystalline phase [12],with not even metastable superfluid phases,just as in 3D;in both cases,no qualitative change takes place,with respect to the threedimensional case.The only ‘deviation’ from this rule is represented by the lighter isotope of helium,namely3He;in 3D,the equilibrium phase at low temperature is a self-bound(superfluid) liquid,whereas in 2D the system only exists in the gas phase [13].While this has significant implications,e.g.,on the phase diagram of isotopic helium mixtures in 2D[14],it can be regarded as a mainly quantitative change,given the structural similarity between the liquid and gas phases,which enjoy the same symmetry.
In this paper,we report the results of a theoretical investigation of a condensed matter system for which the dimensional reduction from 3D to 2D brings about a major,qualitative change in the phase diagram.To our knowledge,this is the first clear-cut example of such an occurrence for a condensed matter system in continuous space,described by a realistic Hamiltonian.The substance is hypothetical,although in principle neither unphysical nor implausible,and it is named muonium hydride.A muonium hydride (HMu)molecule is a bound state of muonium and hydrogen atoms(a muonium atom is one in which a proton is replaced by an anti-muon).Its mass is only slightly more than half the mass of a parahydrogen molecule,and its electronic properties,in its ground state,are very nearly the same as parahydrogen[15,16].It has spin zero,and therefore a system of identical such particles obeys Bose statistics.
The phase diagram of this system in 3D was studied in[17],and was found to be identical to that of parahydrogen,albeit the ground state equilibrium crystalline phase has a remarkably low density,lower than that of4He.Just like for parahydrogen,no evidence of any metastable (super)fluid phase can be found.As shown below,in 2D the situation is entirely different.Our study,based on the same methodology used in [17],namely computer simulations based on the continuous-space Worm Algorithm,shows that HMu has the same low-temperature phase diagram of4He,with an equilibrium liquid phase with a density very close to that of4He,turning superfluid at a temperature T ~2 K.Upon being compressed,the system freezes into a triangular crystal,with a freezing density slightly lower than that of4He.
It is known that quantum-mechanical exchanges of identical particles play a pivotal role in upending the classical picture,which is not otherwise significantly altered by zeropoint motion alone [18].In this particular system,the reduction of dimensionality has the effect of rendering exchanges energetically competitive with respect to the potential energy of the interaction.This is consistent with the observation made in [17] of an enhanced superfluid response in HMu clusters (comprising a few tens of molecules),compared to their parahydrogen counterparts.
Leaving aside the actual experimental feasibility of the observation of the physics studied here,which seems at least presently out of reach,condensed HMu nonetheless represents an interesting,possibly useful‘theoretical data point’,in assessing quantitatively the importance of dimensionality on the thermodynamics of a condensed matter system.
2.Model and methodology
We consider an assembly of N HMu molecules,regarded as point-like,identical particles of mass m and spin S=0,whose motion is restricted to two physical dimensions.The system is enclosed in a rectangular cell of area A=Lx×Ly,with periodic boundary conditions in the two directions,yielding a density n=N/A.The quantum-mechanical many-body Hamiltonian reads as follows:
where the first (second) sum runs over all particles (pairs of particles),λ ≡?2/2m=21.63 K?2,rij≡|ri?rj| and v(r)denotes the pairwise interaction between two HMu molecules.Just as in [17],we model the interaction between two HMu molecules by means of the well-known Silvera–Goldman potential [19],which is the most commonly utilized in microscopic studies of the condensed phase of parahydrogen.This choice of pair potential is based on the same considerations offered in [17],namely (a) the use of a quantitatively more accurate potential is not likely to affect the conclusions of our study in a significant way,and (b) the comparison of the results with those of other calculations(i.e.,those of [17] in 3D) allows us to zero in on the effect of the dimensional reduction alone.
The low-temperature phase diagram of the thermodynamic system described by equation (1) as a function of density and temperature has been studied in this work by means of numerical (path integral Monte Carlo) simulations,based on the continuous-space Worm algorithm [20,21].Since this technique is by now fairly well-established,and extensively described in the literature,we shall not review it here;we used the canonical variant of the algorithm,in which the number of particles N is fixed [22,23].
Details of the simulation are standard,we made use of the fourth-order approximation for the short imaginary time (τ)propagator (see,for instance,[24]),and all of the results presented here are extrapolated to the τ →0 limit.We generally found numerical estimates for structural and energetic properties of interest here,obtained with a value of the time step τ ~3.0×10?3K?1to be indistinguishable from the extrapolated ones,within the statistical uncertainties of the calculation.We carried out simulations of systems comprising a number N of particles equal to 36 and 144.The cell geometry was taken to be square (rectangular,accommodating a perfect triangular crystal)for simulations of the system in the liquid (crystalline) phase.The results for structural and energetic quantities contained with different system sizes are indistinguishable,within the statistical errors of our calculations.
Physical quantities of interest for the bulk calculations include the energy per particle and pressure as a function of density and temperature,i.e.,the thermodynamic equation of state in the low-temperature limit.It is found that,within the statistical errors of our calculation,the results for most quantities remain unchanged below T=1 K,i.e.,results quoted for this temperature can be regarded as essentially ground state estimates.We estimated the contribution to the energy and the pressure arising from pairs of particles at distances greater than the largest distance allowed by the size of the simulation cell by approximating the pair correlation function g(r) with 1 for greater distances.On comparing the results obtained for the two systems of different sizes studied here,we determined this to be a quantitatively accurate procedure.We computed the pair correlation function and the related static structure factor,in order to assess the presence of crystalline order,which can also be detected through visual inspection of the imaginary-time paths.
We probed for possible superfluid order through the direct calculation of the superfluid fraction using the wellestablished winding number estimator [25].To assess the propensity of the system to develop a superfluid response,and its proximity to a superfluid transition,we also rely on a more indirect criterion,namely we monitor the frequency of cycles of permutations of identical particles involving a significant fraction of the particles in the system.While there is no quantitative connection between permutation cycles and the superfluid fraction [26],a global superfluid phase requires exchanges of macroscopic numbers of particles (see,for instance,[27]).
3.Results
We begin with a discussion of the low-temperature energetics of the system.Figure 1 shows the computed energy per molecule e(n)at temperature T=1 K.As mentioned in 2,the results remain unchanged,within the statistical errors of the calculation,or lowering the temperature below 1 K.Therefore,those shown in figure 1 can be considered as ground state estimates.
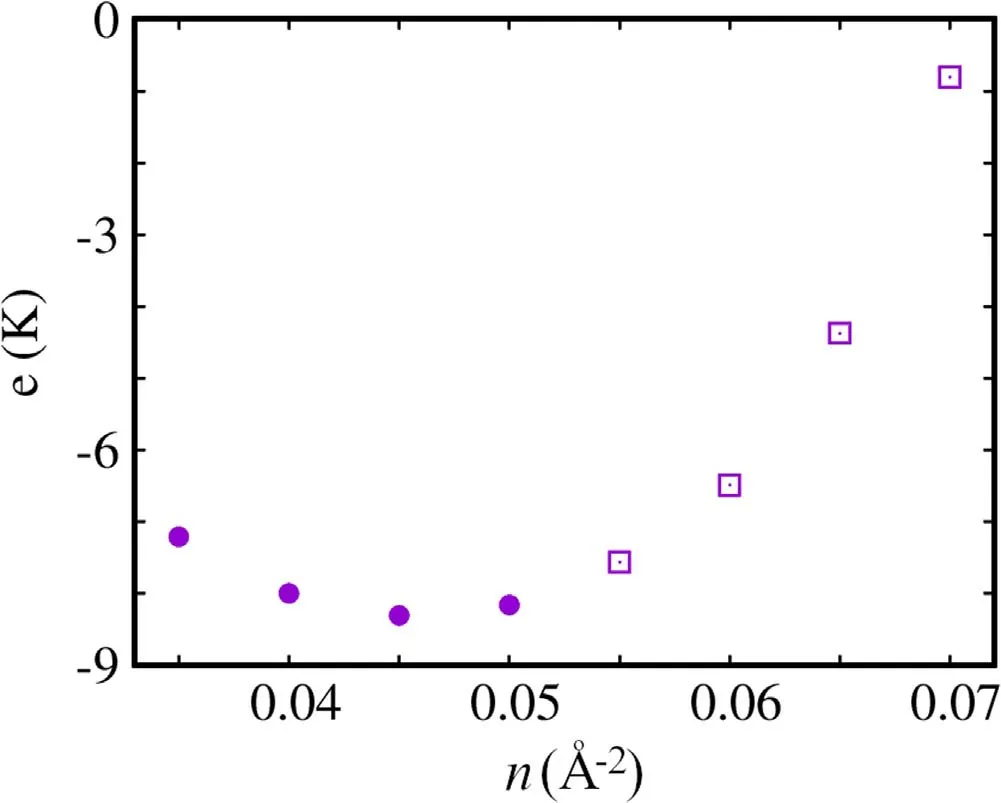
Figure 1.Energy per HMu molecules(in K)computed by simulation at a temperature T=1 K as a function of the density n (in ??2).Open squares refer to thermodynamic points at which the system is in the crystalline phase,filled circles to the superfluid.Statistical errors are smaller than symbol sizes.
The first observation is that the system is self-bound,i.e.,there exists a nonzero equilibrium density n?~0.045 ??2;the binding energy e?~?8.5 K [28].The equilibrium density (magnitude of the binding energy) is approximately 2/3(1/3) of that of parahydrogen in 2D [12].Thus,on going from 3D to 2D the binding energy is more significantly reduced for HMu than parahydrogen.The value of n?is remarkably close to the equilibrium density in 2D of4He[11].The question,of course,is whether the physics of the system at its equilibrium density is closer to that of4He or parahydrogen.We address this issue by examining the structure and the superfluid response.
Figure 2 shows the pair correlation function g(r) computed by simulation at temperature T=1 K for the two different densities n=0.05,0.06 ??2.The qualitative difference between the two cases is clear,and it is important to remember that no a priori physical assumption is built into a finite temperature calculation,i.e.,crystalline order,signaled by the regular oscillations in the g(r) extending to long distances for the higher density,occurs spontaneously,not because of possible simulation bias which affects,for example,ground state Monte Carlo simulations [29,30].
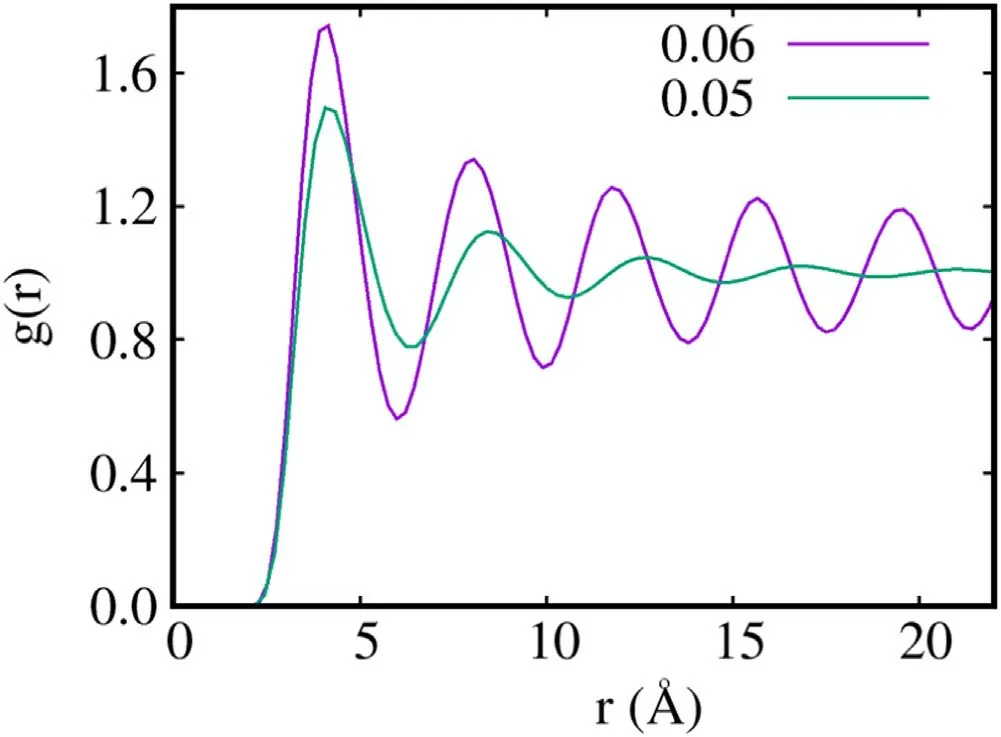
Figure 2.Pair correlation functions computed at T=1 K for the two different densities 0.05 and 0.06 ??2.
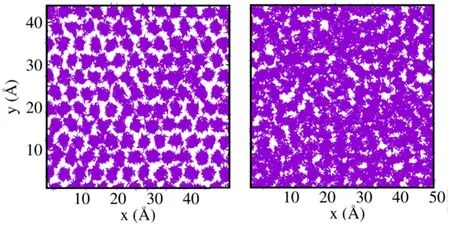
Figure 3.Snapshots of many-particle worldlines for two representative configurations,left (right) illustrating the physics of the crystalline(superfluid) phase of density 0.06 (0.05) ??2 In both cases the temperature is T=1 K.
At the lower value of the density,there is no crystalline order;on the other hand,long particle exchanges set in,involving a large fraction of all the particles in the system.As a result,off-diagonal (quasi) long-range order and a concomitant finite superfluid response appear.All of this is instead absent at the higher density,at which essentially no exchanges take place (no supersolid response is observed).
As mentioned above,additional and perhaps more intuitive insight can be provided by a direct,visual inspection of many-particle configurations generated by the sampling.An illustration is provided in figure 3,which shows two such representative ‘snapshots’,the left (right) for the system at density 0.06 (0.05) ??2.In both cases,the temperature is T=1 K.In the right snapshot,which refers to the lower density,particles are delocalized and their worldlines are highly entangled,i.e.,exchanges of identical particles occur frequently [27].This can be contrasted with what happens in the crystalline phase(left panel of figure 3),in which particles are localized at lattice sites;exchanges occur infrequently and remain local in character,hence no global superfluid response arises.Indeed,no ‘supersolid’ behavior is observed in HMu,just as in parahydrogen,consistent with the current understanding of supersolidity which requires that the interaction among particles feature a ‘soft’ repulsive core at short distances [31].
The superfluid transition that takes place in the fluid phase conforms to the well-known Berezinskii–Kosterlitz–Thouless[2,4,32]paradigm.Figure 4 displays the estimates for the superfluid fraction ρS(T) as a function of temperature,calculated by simulation for a system comprising N=144 HMu molecules.The fit to the data is obtained following the procedure outlined in[33].Based on the fit to the data for the finite system,one can infer the behavior in the thermodynamic limit,shown by the solid curve in figure 4,and with the aid of the well-known universal jump condition [4],we estimate the superfluid transition temperature Tcto be approximately 2.2 K (a consistent estimate is obtained,using the same procedure,based on the results for a system of N=36 particles).This can be compared to the value of Tc≈0.65 K for4He in 2D.The enhancement of the critical temperature of HMu,with respect to that of4He,arises from the combination of lower mass and stronger interaction,in turn resulting in a relatively high equilibrium density.
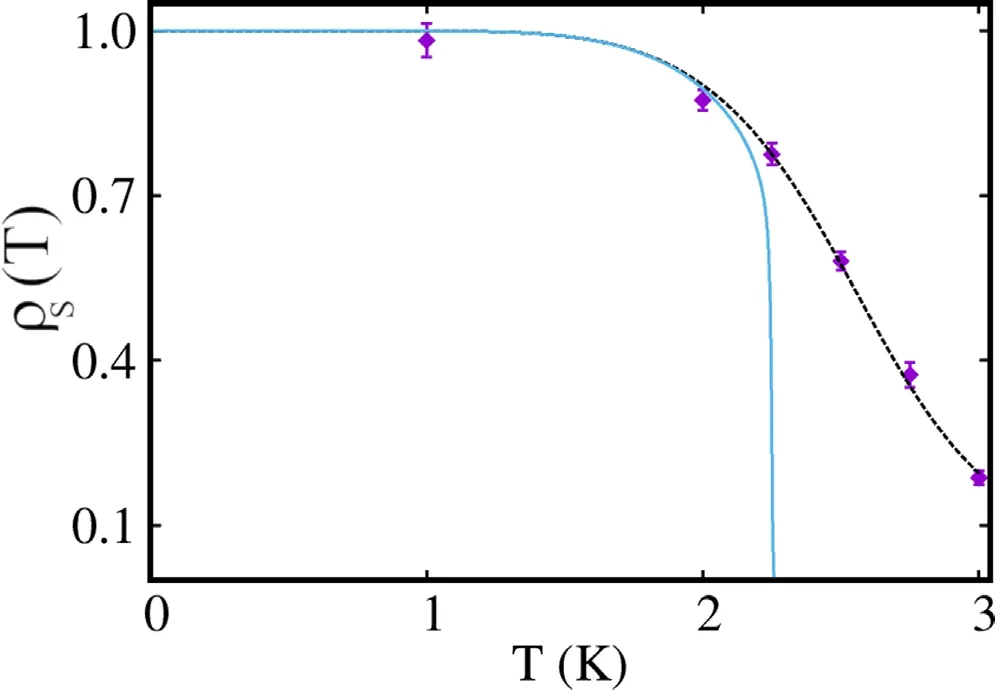
Figure 4.Superfluid fraction ρS(T)as a function of temperature,for a system comprising N=144 HMu molecules.Diamonds are values computed by simulation,the dotted line is a fit to the data based on the BKT recursive equations (see text),while the solid line represents the extrapolation to the thermodynamic limit.When not shown,statistical errors are smaller than the symbol size.
4.Discussion
We have investigated the low-temperature phase diagram of a bulk muonium hydride in 2D,by means of unbiased,reliable quantum simulations.Our model assumes a pairwise,central interaction among HMu molecules identical to that of H2molecules.Quantitative arguments have been offered in [17]in support of this assumption.Moreover,the use of the same potential utilized in[17]allows one to isolate the effect of the dimensional reduction (from 3D to 2D),which is the main subject of our study.
The significant(in our view)outcome of this study is the radically different physics that the system displays in 2D and 3D.To our knowledge,this is the first clear-cut example of dimensional reduction altering the bulk phase diagram of a substance as observed in this work.While in 3D HMu is a crystal,and its phase diagram is virtually identical to that of parahydrogen (albeit with a remarkably low equilibrium density),in 2D its phase diagram mimics that of4He,with a ground state superfluid equilibrium phase which crystallizes only on compression,and with a remarkably high critical temperature,above 2 K.In other words,the physical scenario once deemed possible,but which is not realized for parahydrogen,is predicted to take place for muonium hydride,at least as described by the model considered here.
What causes the equilibrium phase of HMu to be a(super)fluid in 2D,but a crystal in 3D?It is known that a Bose system can lower its (kinetic) energy through quantummechanical exchanges involving a macroscopic number of particles.This physical mechanism drives the system to lower density,as exchanges can take place only if particles are,on average,sufficiently far apart from each other to avoid the repulsive core of the pair-wise interaction at short inter-particle separation.As shown in [18],this is ultimately what causes4He not to crystallize at low temperature.The energy reduction arising from exchanges compensates for the increase in potential energy of interaction due to the lowering of the density (as the system does not take full advantage of the attractive part of the pair-wise interaction).
This occurs in helium because of the relative weakness of the interatomic pair potential,whereas in parahydrogen,the combination of greater well depth and hard core radius render the same scenario energetically disadvantageous,which is why the equilibrium phase is a crystal,even in 2D.The lower mass of HMu,on the other hand,renders the competition between exchange and potential energy altogether favorable to the lower density (fluid) phase in 2D,due to the reduced coordination number.
The experimental feasibility of the system considered here appears severely hampered by the very short lifetime of the μ+(of the order of a μs),replacing one of the two protons of a parahydrogen molecule,resulting in one of muonium hydride.To be sure,the production of a single,or few HMu molecules has already been demonstrated;indeed,‘muonium chemistry’ has been a legitimate,active area of research for quite some time [34].However,assembling a sufficiently large number of such objects in some restricted region of space,in order to carry out meaningful observations of condensed matter effects (a challenge in many respects reminiscent of those faced by cold atom experimenters),seems a truly daunting task.
Still,even if it were to be regarded exclusively as a‘toy’system,HMu can still prove a useful theoretical construct,both as a limiting case as well as offering nontrivial insight into the interplay between superfluid and crystalline orders.Of particular interest,for example,is the study (e.g.,by means of computer simulation) of layering,and the emergence of solid order,as successive superfluid layers of HMu are adsorbed on a substrate.
One might wonder whether the main physical effect described in this paper could conceivably be observed in some other Lennard–Jones-type system.On this point,we note that the value of the above-mentioned Λ parameter is~0.07 for HMu,to be compared to 0.09 for4He and ~0.04 for parahydrogen.One might think of realizing such a value in a system of cold atoms,in which the main parameters of the interaction could be suitably engineered,e.g.,by making use of the Feshbach resonance [35].
Acknowledgments
This work was supported by the Natural Sciences and Engineering Research Council of Canada,and by the China Scholarship Council.The computer codes utilized to obtain the results can be obtained by contacting the authors.The authors declare no conflict of interest.
ORCID iDs
 Communications in Theoretical Physics2024年2期
Communications in Theoretical Physics2024年2期
- Communications in Theoretical Physics的其它文章
- Finite dimensional irreducible representations of Lie superalgebra D (2,1;α)
- Correlation between mechano-electronic features and scattering rates using deformation potential theory
- The size effect and analogous boundary states in a circular non-Hermitian chain
- The modeling non-sequential double ionization of helium atom under highintensity femtosecond laser pulses with shielding charge approximation
- Non-static plane symmetric perfect fluid solutions and Killing symmetries in f(R,T)gravity
- Thermodynamic geometry of the RN-AdS black hole and non-local observables
