Asynchronous gain-scheduled control of deepwater drilling riser system with hybrid event-triggered sampling and unreliable communication?#
Na PANG,Dawei ZHANG,Shuqian ZHU
School of Mathematics, Shandong University, Jinan 250100, China
Abstract: This paper investigates the recoil control of the deepwater drilling riser system with nonlinear tension force and energy-bounded friction force under the circumstances of limited network resources and unreliable communication.Different from the existing linearization modeling method,a triangle-based polytope modeling method is applied to the nonlinear riser system.Based on the polytope model,to improve resource utilization and accommodate random data loss and communication delay,an asynchronous gain-scheduled control strategy under a hybrid event-triggered scheme is proposed.An asynchronous linear parameter-varying system that blends input delay and impulsive update equation is presented to model the nonlinear networked recoil control system,where the asynchronous deviation bounds of scheduling parameters are calculated.Resorting to the Lyapunov–Krasovskii functional method,some solvable conditions of disturbance attenuation analysis and recoil control design are derived such that the resulting networked system is exponentially mean-square stable with prescribed H∞performance.The obtained numerical results verified that the proposed nonlinear networked control method can achieve a better recoil response of the riser system with less transmission data compared with the linear control method.
Key words: Riser system;Recoil control;Asynchronous gain-scheduled control;Data loss;Event-triggered scheme
1 Introduction
The deepwater drilling riser system is a class of key marine engineering equipment that connects offshore drilling platforms and underwater wellhead systems during drilling operations.To ensure the safety of equipment and platform staffwhen facing the extremely harsh ocean environment or the failure of dynamic positioning systems,the riser system is required to implement the emergency disconnection between the lower marine riser package and the subsea blowout preventer.In this situation,the riser quickly recoils upwards,and this recoil,caused by elastic potential energy and friction resistance of drilling fluid,is named the recoil response (Liu XQ et al.,2022;Wang XL et al.,2022).If the recoil response is not properly suppressed,the platform staffand the riser equipment are in great danger.
In the past decade,considerable effort has been put into addressing the recoil response suppression of riser systems (Pestana et al.,2016;Liu J et al.,2018;Wang T and Liu,2018;Liu XQ et al.,2021;Wang XL et al.,2021,2022).In the prevalent literature dealing with the topic,the main challenging problems pertain to the means of characterizing the coupled dynamics model of the recoil control process and that of designing the efficient control strategies for satisfactory response suppression.In Liu XQ et al.(2020,2021),Meng et al.(2020),and Zhao et al.(2022a,2022b),using the finite element method and the concentrated mass method,a linear spring-mass-damping model was used for axial dynamic analysis of risers.With such a linear model,to suppress the effect of friction force on recoil response,Zhao et al.(2022a)designed a pure delayedH∞controller(PDHC),Zhao et al.(2022b)designed an optimal recoil controller with feedforward compensation,Zhang W et al.(2023a)proposed an observer-based dynamic output-feedback controller,and Zhang W et al.(2023b)proposed a delayed state-feedbackH∞controller.In fact,the tension force produced by the tensioner is essentially nonlinear(Pestana et al.,2016;Wang T and Liu,2018;Liu XQ et al.,2021).Although the linearization method based on the Taylor expansion is commonly used to model the risertensioner system (Zhao et al.,2022a,2022b;Zhang W et al.,2023a,2023b),it unavoidably causes an unsatisfactory control performance by the linear recoil control strategies when linearization errors are ignored.Thus,it is particularly necessary to present some specialized nonlinear modeling and recoil control methods for the riser-tensioner system.
Notice that the existing recoil control strategies so far have been designed in a traditional control system structure.From the perspective of modern industrial control,the prevalent networking technology and networked control system (NCS) structure can bring revolutionary progress and attractive advantages such as remote control and diagnostics,flexible system layout,and low implementation cost(Ma et al.,2019;Zhang XM et al.,2020;Shi et al.,2021).Since offshore drilling platforms tend to operate in a deep-sea field to explore more oil or gas resources,the operational environment of the drilling riser system poses some significant challenges to stability and safety(Dinh et al.,2017;He et al.,2020;Liu Y et al.,2022).Currently,the satellite communication network and other dedicated wireless ad-hoc networks are used mainly to deploy the network environment of marine engineering equipment in a deep-sea environment.Such types of networks are with limited resources and relatively low reliability,and they can impose imperfect constraints such as communication delay and random data loss,which further affect the control performance (Zou et al.,2016;Hu et al.,2020;Zhang DW et al.,2020;Zhang XM et al.,2022,2023).Accordingly,it is necessary to develop some networked nonlinear modeling and recoil control methods of riser-tensioner systems that can be deployed under the circumstances of limited network resources and unreliable communication (Coutinho and Palhares,2021;Zhang BL et al.,2021).
This paper proposes several networked recoil control system modeling and asynchronous gainscheduled control methods for riser-tensioner systems subject to limited network resources,unavoidable communication delay,and unreliable communication.Since the nonlinear riser-tensioner system in the existing forms depends on the displacement of the first mass block that is physically measurable,an equivalent form of the nonlinear riser-tensioner system is reformulated by a triangle-based polytope model inspired by the nonlinear modeling advantage of linear parameter-varying (LPV) systems (Li WF et al.,2020;Chu et al.,2022).To save network resources and against the random data loss,the hybrid event-triggered sampling scheme in Gao et al.(2023) is introduced to collect the necessary displacement and velocity information of the risertensioner system.Considering that the LPV model with the schedulable displacement information and the transmitted information is affected by the communication delay and the possible data loss,an asynchronous gain-scheduled control scheme is presented to implement the networked control.The resulting nonlinear NCS of the riser-tensioner system is modeled by an asynchronous parameter-scheduled system with sampling and random impulsive updates.For such a system,a computation method of the asynchronous deviation bounds of the scheduling parameters is provided and a discontinuous Lyapunov–Krasovskii functional method is applied to derive anH∞performance analysis criterion.Using the deviation bounds and the analysis results,a nonlinear design of the asynchronous gain-scheduled controller(AGSC) is developed.Finally,the NCS modeling and recoil control methods of the riser-tensioner system are numerically verified.
The main contributions of the present research are summarized below:
1.A specialized nonlinear NCS modeling method of the riser-tensioner system subject to event-triggered scheme,communication delay,and random data loss is proposed by applying the LPV system approach and the hybrid sampled-data system and impulsive system approach.
2.An asynchronous gain-scheduled control strategy is presented to suppress the recoil response of the networked riser-tensioner system with friction force as much as possible in theH∞control sense.
3.A case study is carried out,which reveals that the proposed nonlinear networked recoil control method,compared with the common linear control method,can achieve a better control effect and suppression performance in the network environment,and can save network resources with the eventtriggered scheme.
2 Nonlinear networked control system modeling and recoil control of the risertensioner system
2.1 Triangle-based polytope linear parameter-varying model of the risertensioner system
Usually,the deepwater drilling riser-tensioner system is simplified as a spring-mass-damping model with three degrees of freedom (Wang YB and Gao,2019;Liu XQ et al.,2021;Zhao et al.,2022a,2022b),and the dynamic equations of the model are given by
with the following model of the tension forceF(t)(Liu XQ et al.,2021):
Here,x0=(PH0Ar-PL0Ap-m1g+Fb1)/k2;mi’s(i=1,2,3) represent three equivalent mass blocks;ci(i=1,2,3) is the damping coefficient;xi(t)(i=1,2,3)is the displacement at timet;ki(i=2,3)is the stiffness;gis the acceleration of gravity;Fwi(t)andFmi(t) (i=1,2,3) are the friction forces of seawater and drilling mud discharge,respectively;Fbi’s (i=1,2,3)denote the axial buoyancy of three mass blocks;PH0andPL0are the pressures of the high-and low-pressure gas at the initial moment,respectively;VH0andVL0are the volumes of the high-and low-pressure gas at the initial moment,respectively;ArandApare the areas of piston at the rod and rod-less sides,respectively;κis a constant relative to the properties of gas and it is generally assumed to beκ=1;u(t) is the pressure drop generated by the recoil control.
Clearly,F(t) is nonlinear with respect tox1(t),which results in the riser-tensioner system(1) being a nonlinear system.Usually,a linearization method based on the Taylor expansion is adopted to convert system (1) to a linear system with the sacrifice of approximation accuracy (Zhao et al.,2022a,2022b;Zhang W et al.,2023a,2023b).To better model the nonlinearity,the LPV system modeling method is proposed as follows.Let
Using Eq.(1),the initial displacement values at the moment of emergency disconnection are given by
and the equilibrium point is computed by
The initial state of system(3)is denoted asz(0)=z0.By solving the external forceh(t)in a manner similar to that was adopted in Li CW et al.(2016)and Zhao et al.(2022a,2022b),one further obtains the risertensioner system:
Here,Fw(t) andFm(t) are the friction forces of seawater and drilling mud discharge,respectively;ρwandρmare the densities of seawater and drilling mud discharge,respectively;fwandfmare the friction coefficients of seawater and drilling mud discharge,respectively;Lw(t)andLrare the length of seawater section at timetand the length of the riser,respectively;v(t) is the discharge velocity at timet;Δtis the time increment;a(t) is the average acceleration in each time step fromt-Δttot;Asis the hydraulic area of the riser;Deis the diameter of the riser.
Note thatA(z1(t)) is a time-varying nonlinear matrix with respect to boundedz1(t).Inspired by Gao et al.(2022),a triangle-based polytope modeling method is introduced by designing the scheduling variables.The specific modeling process is stated as follows:
where the scheduling parameter?i(t)(i=1,2,3)and the coefficient matrixAi(i=1,2,3)can be obtained using the following lemma:
Lemma 1Define the following notations:
Then the parameters and matrices in system(5)can be computed by
2.2 Networked asynchronous gain-scheduled control formulation
For the LPV system(5),the following controller is proposed:
whereKi(i=1,2,3) is the control gain to be designed.To save communication resources and tolerate the random data loss(Ge et al.,2019,2020,2021,2022;Jiang et al.,2021;Sun et al.,2021;Wei et al.,2021;Liu ZQ et al.,2022),the hybrid event-triggered sampling scheme in Gao et al.(2023) is introduced as follows:
wherehis the sampling period,σ>0 is the threshold coefficient,T>0 is the weighting matrix,κ is the fixed triggering size,and N is the set of natural numbers.As shown in Gao et al.(2023),the main advantages of the event-triggered scheme (7)lie at solving the problem of random data loss of triggered data,providing a balanced choice between the fixed triggering size and the data loss probability,and improving the transient and steady performance.In scheme (7),Tcan be co-designed with the control design result,and the parameters κ andσare pre-set.As κ is inversely proportional to the maximum allowable data loss probability,one can set the value of κ according to rental network protocols.σcan be freely adjusted to satisfy 0<σ<1,meeting the expected transmission efficiency.Notice that the scheduling parameter?i(t) (i=1,2,3)in controller (6) is the function of the displacement informationz1(t) to be sampled and transmitted.Since the triggered scheme(7)is introduced,the data?i(tkh) are available for control computing.Due to the effect of inevitable communication delayτtkand possible random data loss,the scheduling parameters cannot be shared synchronously between the system and the controller.Thus,the control input is constructed as follows:
fort ∈{tkh+τtk}k∈N,where(tkh)=βkz(tkh)+(1-βk)(tk-1h) (?k ∈N),(t-1h)=0 is set to compute the triggered data(t0h),andβkis a stochastic variable obeying the Bernoulli distribution with the probabilities Prob{βk=1}=βand Prob{βk=0}=1-βwithβ ∈(0,1].Using the input delay method,one can transform the control input (8)into
2.3 Networked riser-tensioner system and recoil control problem statement
Substituting the control input (9) into system (5),the networked riser-tensioner system with asynchronous gain-scheduled control is derived as
fort ∈Fk,i(i=0,1,...,Jk,?k ∈N) with the reset equations
The initial condition is supplemented asz(t)=z(t0h)(t ∈[t0h-ηM,t0h])andd(t0h)=-z(t0h).
To suppress the adverse impact of friction force on the relative displacementzi(i=1,3,5) and ensure the safety of the riser system during the recoil response of the riser-tensioner system,the controlled output of system (10) is introduced as (Zhao et al.,2022a)
Therefore,the recoil control problem of the networked riser-tensioner system can be stated as follows:
AGSC (9) is designed such that (1) the system (Eqs.(10) and (11)) subject to condition (12)is exponentially mean-square stable whenh(t)=0;i.e.,the following inequalities hold for someυi>0(i=1,2):
(2) Under the zero initial condition,E{‖η(t)‖2} ≤γ‖h(t)‖2holds for the nonzeroh(t) and the prescribedH∞performance levelγ>0.
3 Main results
In this section,Lemma 2 shows a computing method of the asynchronous deviation bounds,and Theorems 1 and 2 provide the disturbance attenuation analysis and asynchronous gain-scheduled control design,respectively.
3.1 Computing method of asynchronous deviation bounds of scheduling parameters
Lemma 2For givenηM>0 and?i(t) (i=1,2,3)given in Lemma 1,the following inequality holds:
where the asynchronous deviation boundμi=min{1,ηMvi}(i=1,2,3)and
ProofIt is clear that
Based on the functional relations between?i(t) andz1(t)given in Lemma 1,one has|?i(t)-?i(t-τ(t))|≤ηMvi(i=1,2,3) from condition (15).Considering 0≤?i(t)≤1 (i=1,2,3),one can complete the proof.
3.2 Disturbance attenuation analysis of the networked riser-tensioner system
Theorem 1For given positive scalarsh,τM,ηM,γ,κ,σ ∈(0,1),β ∈(0,1],μi ∈[0,1] (i=1,2,3),and matrixKi(i=1,2,3),the system (Eqs.(10)and (11)) subject to condition (12) is exponentially mean-square stable withH∞performanceγ,if there exist symmetric matricesP>0,Q>0,R>0,S>0,T>0,H<0,W>0,Gi>0(i=1,2,3),Mi>0(i=1,2,3),Ni>0(i=1,2,3),and matricesUi(i=1,2,3)andXi(i=1,2)such that the following linear matrix inequalities (LMIs) hold forl=1,2,3,4 andi,j=1,2,3:
whereΠi ∈R2n×2n(i=1,2),Π3∈R3n×3n(n=6),Ξlij ∈R(12n+1)×(12n+1)(l=1,3),Ξlij ∈R(14n+1)×(14n+1)(l=2,4),H(i,j)∈R3n×3n(i,j=1,2,...,6) are block matrices,R denotes the set of real numbers,and (?)(s,t) represents the block matrix of thesthrow andtthcolumn of matrix (?).In addition,
Here,Sym{?}=?+?T.The proof of Theorem 1 is given in the supplementary materials.
3.3 Nonlinear design of the networked AGSC
Theorem 2For a given scalar?,and positive scalarsh,τM,ηM,γ,κ,σ ∈(0,1),β ∈(0,1],μi ∈[0,1] (i=1,2,3),there exists controller (6),which can ensure that the system(Eqs.(10)and(11))subject to condition (12) is exponentially mean-square stable withH∞performance levelγ,if there exist symmetric matrices>0,>0,>0,>0,>0,<0,>0,>0 (i=1,2,3),>0(i=1,2,3),>0 (i=1,2,3),and matrices(i=1,2,3),X,andYi(i=1,2,3),such that the following LMIs hold forl=1,2,3,4 andi,j=1,2,3:
The proof of Theorem 2 is given in the supplementary materials.
Remark 1The differences between the proposed results and the existing ones in Zhao et al.(2022a,2022b) and Zhang W et al.(2023a,2023b) are reflected in two aspects: (1) The system models and corresponding recoil control methods of the risertensioner system are different.In Zhao et al.(2022a,2022b) and Zhang W et al.(2023a,2023b),a linearization method based on the Taylor expansion was used to deal with the nonlinear tension force of the tensioner and linear control strategies were proposed for the linearized riser-tensioner system,while a nonlinear LPV system is presented in this study to equivalently describe the nonlinear tension force and a nonlinear controller is tailored to handle the modeling nonlinearity.(2) The system framework and control constraints are different.In Zhao et al.(2022a,2022b) and Zhang W et al.(2023a,2023b),a traditional system control architecture of the riser-tensioner system was discussed,while the NCS paradigm is considered in this study and the effect of event-triggered communication,data loss,and communication delay on control performance is investigated.In particular,the traditional recoil control method of the riser-tensioner system does not work in the NCS framework,as will be illustrated in the numerical example.
Remark 2The analysis and design results,i.e.,Theorems 1 and 2,are applicable to general LPV systems if Lemma 2 can be applied.In this case,it is necessary to update the system matrices inrevise the size ofn,and adjust the corresponding dimensions of matrix variables.Since the scheduling parameters in general LPV systems are usually functions of system states and the upper boundηMis prior knowledge,condition (14)in Lemma 2 can be satisfied.
4 Simulation results
In this section,we provide numerical results to demonstrate that the proposed nonlinear recoil control method is characterized by less conservatism and a better control effect in comparison with the existing linear control method.
First,the parameter values of the riser-tensioner system (Eqs.(1) and (2)) are listed in Table 1.Using these parameter values,the system matrices in Eq.(5) can be easily calculated.It is assumed that the displacement and velocity of the riser-tensioner system satisfy-6 m≤zi(t)≤2.5 m(i=1,3,5),-2 m/s≤zi(t)≤2.5 m/s (i=2,4,6).Using Lemma 2,one can obtain the asynchronous deviation boundμi(i=1,2,3)for a givenηM.
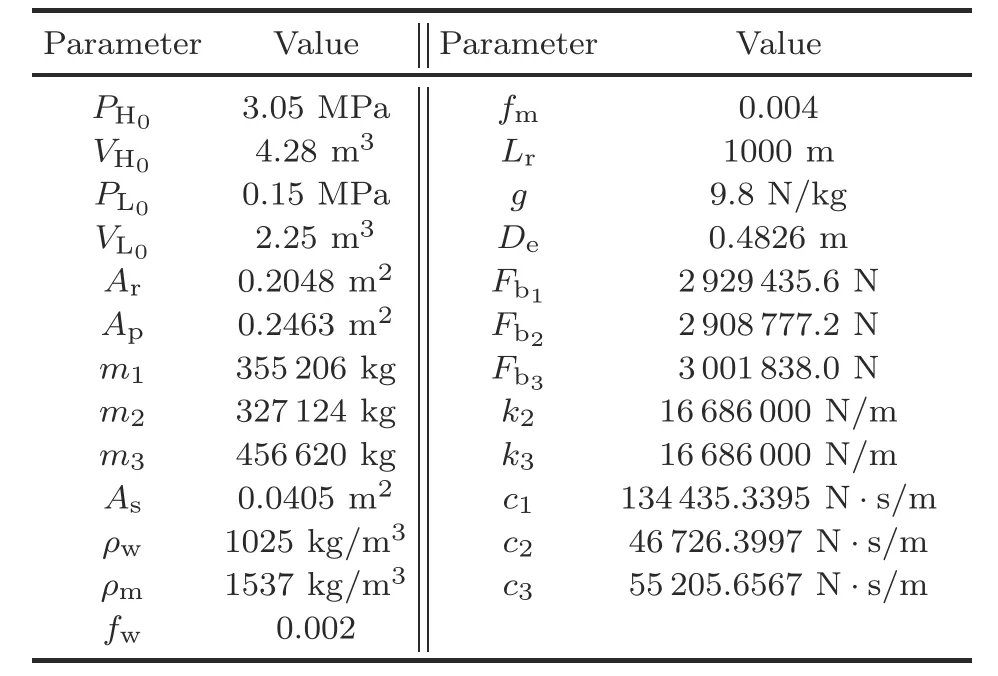
Table 1 Numerical values of physical parameters in the riser-tensioner system (Zhao et al.,2022a,2022b)
Second,we evaluate the solvability of the proposed nonlinear control design and the linear control design in Zhao et al.(2022a).Using the design method in Zhao et al.(2022a),a linear PDHC is proposed for a riser-tensioner system,where PDHC means that a pure time-varying delayτ(t)satisfying 0≤τ(t)≤ηMis artificially introduced into the control inputu(t)=Kz(t-τ(t)) under a traditional system framework.Concerning the present research,Theorem 2 can provide a nonlinear AGSC for the networked riser-tensioner system.For givenγ=1.0,the maximum allowable delay bound (MADB) can be obtained asηM=0.095 s by using the method in Zhao et al.(2022a).For givenγ=1.0,h=0.01 s,κ=0.2 s,β=0.9,σ=0.1,and?=0.2,the MADB can be obtained asηM=0.395 s by using Theorem 2.From the design feasibility,one can ascertain that the proposed nonlinear control design method is less conservative than the linear control design method in Zhao et al.(2022a).
Third,we demonstrate that the proposed nonlinear AGSC can achieve a better recoil control effect of the networked riser-tensioner system than the linear PDHC in Zhao et al.(2022a).In the following,we will compare the control effect of nonlinear AGSC and linear PDHC in two cases ofηM.
Case 1:ηM=0.095 s.This involves using the method in Zhao et al.(2022a)to obtain the minimumγmin=0.002 and the following control gain:
Such a controller is denoted by PDHC-0095.
Underh=0.01 s,κ=0.2 s,β=0.9,σ=0.1,and?=0.2,Theorem 2 can be used to obtain the minimumγmin=0.001 75 and the following control gains:
Such a controller is denoted by AGSC-0095.
Case 2:ηM=0.395 s.Underγ=1.0,h=0.01 s,κ=0.2 s,β=0.9,σ=0.1,and?=0.2,Theorem 2 can be used to obtain the following control gains:
Such a controller is denoted by AGSC-0395.In this case,the design method in Zhao et al.(2022a)is not feasible.
In simulations,for given Δt=0.01 s,a(0)=0 m/s2,v(0)=0 m/s,andLw(0)=0 m,the external forceh(t) in system (4) is approximately solved by using the whole fluid model of drilling mud discharge in Li CW et al.(2016)and Zhao et al.(2022a,2022b).The recoil responses of the riser-tensioner system with the designed controllers in cases 1 and 2 are depicted in Figs.1 and 2,respectively.As demonstrated in Fig.1,forηM=0.095 s,the achieved stabilizing transient time is approximately 10,60,and 80 s,corresponding to the AGSC-0095 designed in the present study,the PDHC-0095 introduced in Zhao et al.(2022a),and absence of controller,respectively.It indicates that AGSC-0095 ensures a better recoil response of the riser-tensioner system compared with PDHC-0095 and absence of control.Meanwhile,the simulation valueγsimand the theoretical valueγminof theH∞performance index provided by AGSC-0095 and PDHC-0095 are compared in Table 2,which verifies that AGSC-0095 can ensure a better interference rejection capability.WhenηM=0.395 s,the stabilizing transient time of the AGSC-0395 is about 60 s,while the design method in Zhao et al.(2022a) does not work.Based on the simulations conducted for the two cases,one can conclude that the proposed networked LPV controller can satisfactorily complete the control task and effectively suppress the recoil response of the risertensioner system,compared with the existing linear recoil controller.For givenβ=0.9 and κ=0.2 s,Figs.3 and 4 depict the release time and release interval of the hybrid event-triggered scheme (12) in cases 1 and 2,respectively.It can be seen that the sampled dataz(tkh+κ) (?k ∈N) are compulsorily triggered when κ=0.2 s is reached.The advantage that the proposed event-triggered control can tolerate the random data loss of triggered data is verified.WhenηM=0.095 s (or 0.395 s),the average data transmission interval of AGSC-0095(or AGSC-0395)can be calculated as 0.0506 s(or 0.0606 s)and the amount of data transferred of AGSC-0095 (or AGSC-0395) is reduced by 80.2500% (or 87.6250%)in comparison with the results obtained for the timetriggered control withh=0.01 s.The advantage that the proposed event-triggered control can significantly save communication and computing resources is also confirmed.

Fig.1 Displacements and control force of the riser system without control,with AGSC-0095,and with PDHC-0095
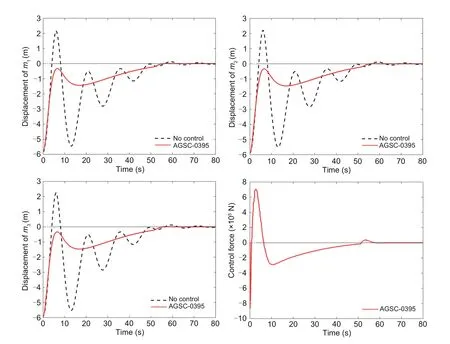
Fig.2 Displacements and control force of the riser system without control and with AGSC-0395
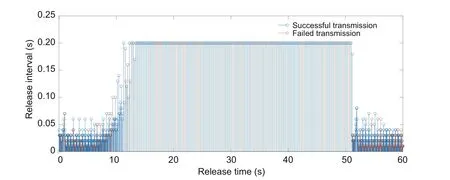
Fig.3 Release time and release interval when κ=0.2 s, β=0.9,and ηM=0.095 s (References to color refer to the online version of this figure)
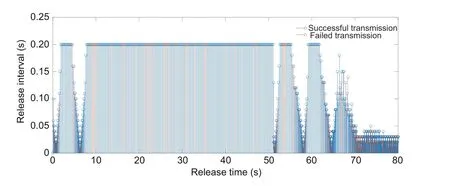
Fig.4 Release time and release interval when κ=0.2 s, β=0.9,and ηM=0.395 s (References to color refer to the online version of this figure)
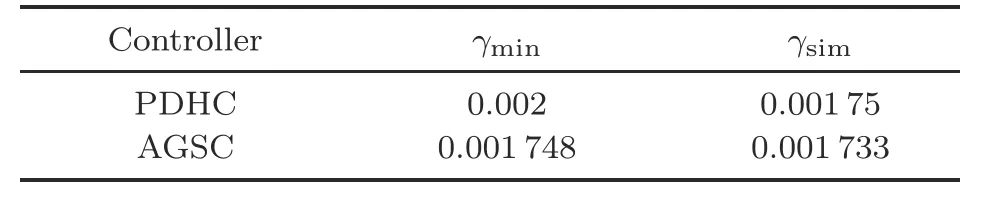
Table 2 H∞performance indexes of the asynchronous gain-scheduled controller (AGSC) and pure delayed H∞controller (PDHC) with τM=0.095 s
5 Conclusions
This paper has proposed nonlinear networked system modeling and asynchronous gain-scheduled control methods of the riser-tensioner system with event-triggered sampling,communication delay,and random data loss.The nonlinearities from the tension force have been modeled by a triangle-based polytope LPV system.The networked constraints have been reflected by an asynchronous parameterscheduled system with sampling and random impulsive updates.To suppress the recoil response of the riser-tensioner system subject to friction force and network constraints,an asynchronous gainscheduled control design algorithm that depends on deviation bounds has been proposed in theH∞control sense.Numerical results have been provided to verify that the nonlinear networked system modeling and control methods are better than the linear control method.
Contributors
Dawei ZHANG and Shuqian ZHU designed the research.Na PANG processed the data and drafted the paper.Dawei ZHANG and Shuqian ZHU revised and finalized the paper.
Compliance with ethics guidelines
Na PANG,Dawei ZHANG,and Shuqian ZHU declare that they have no conflict of interest.
Data availability
The data that support the findings of this study are available from the corresponding author on reasonable request.
List of supplementary materials
1 Proof of Theorem 1
2 Proof of Theorem 2
 Frontiers of Information Technology & Electronic Engineering2024年2期
Frontiers of Information Technology & Electronic Engineering2024年2期
- Frontiers of Information Technology & Electronic Engineering的其它文章
- Secure control and filtering for industrial metaverse
- The engineering of circular causality for specialization and design of complex systems:cad2CAS and casCAD2?
- A low-noise,high-gain,and large-dynamic-range photodetector based on a JFET and a charge amplifier*
- A novel topology with controllable wideband baseband impedance for power amplifiers?
- Empowering smart city situational awareness via big mobile data?
- Estimation of Hammerstein nonlinear systems with noises using filtering and recursive approaches for industrial control*
