Identifying influential spreaders in social networks: A two-stage quantum-behaved particle swarm optimization with L′evy flight
Pengli Lu(盧鵬麗), Jimao Lan(攬繼茂), Jianxin Tang(唐建新)1,,?, Li Zhang(張莉),Shihui Song(宋仕輝), and Hongyu Zhu(朱虹羽)
1Wenzhou Engineering Institute of Pump&Valve,Lanzhou University of Technology,Wenzhou 325100,China
2School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China
Keywords: social networks, influence maximization, metaheuristic optimization, quantum-behaved particle swarm optimization,L′evy flight
1.Introduction
As the pandemic spread around the world, lifestyles and the ways in which people obtain information were unexpectedly transferred to online mediums.[1]The virtual world has provided essential services, while reducing the distance between individuals.In particular,online social platforms,such as Facebook,WeChat,and TikTok,have promoted the growth of information consumption with the growing number of users and have nourished the emergence of online viral marketing on social networks.
While online social networks provide convenience to the users, they also offer opportunities to companies to market their products.[3]Generally, companies first select a group of influential individuals as adopters and give them free access to the product in the expectation that they will recommend the product to their family and friends through word of mouth.If there are strong connections among these users to sustain the exponential spread of the message, then the viral marketing campaign will probably be successful and the referral behavior will, partly, influence the final choice of the purchasers.This scenario has applications in practical campaigns, such as rumor restriction,[4]where one would identify the superspreaders of rumors and restrict them to reduce the risk to society.
Due to the inherent heterogeneity of individuals and the different ways of communication,the influence maximization(IM)problem here refers to the selection of a set of independent individuals that can maximize the coverage of information dissemination through the social relationships among the individuals.
The IM problem was first proposed by Domingos and Richardson,[5]who suggested that we should consider the consumer market as a social network and model it as a Markov random field.Researchers have since proposed a series of IM algorithms to conduct an in-depth study.Kempeet al.[6]proved that the optimization problem of selecting the most influential nodes is NP-hard under the independent cascade(IC)model and linear threshold (LT) model, and proposed a natural greedy strategy, promising that the obtained solution is approximately within 63% of the optimal based on submodular function analysis.However, to accurately evaluate the marginal gain of influence of each candidate node,thousands of Monte Carlo simulations are required in each round of seed selection.This leads to the high time complexityO(knmR)of the algorithm.In particular,the running time of the algorithm increases exponentially with the increase of the network scale,thereby limiting its application in large-scale social networks.
Researchers have subsequently tried to directly selectknodes as influential nodes according to the network topology features,such as degree centrality,[7]PageRank,[8]and so on.Alshahraniet al.[9]tried to combine the local influence with global influence of each node by using classical centrality metrics and proposed two algorithms, which are called Max-CDegKatzd-hops and MinCDegKatzd-hops.However, the approach of using network topology centrality fails to provide stable performance guarantees due to the lack of diversity in the selected nodes in different networks.In addition,community-based approaches have been developed to find influential nodes in the network.Bozorgiet al.[10]considered the influence of nodes within communities as a local influence and the influence of communities in the whole network as a global influence, and proposed INICIM to evaluate influential nodes by combining global influence and local influence.Caiet al.[11]explored the community property to improve the efficiency of the algorithm and proposed a communitybased greedy algorithm to identify the seed nodes.The advantage of community-based methods is that they provide a good trade-off between influence propagation and runtime.However, there are two problems: first,there is a lack of effective strategies to reduce the search space when selecting select seed nodes in large networks; and second, some of the algorithms suffer from the community overlap problem.
In recent years, metaheuristic algorithms have been proposed to efficiently solve the IM problem.Zareieet al.[12]defined the cost function as the influence of nodes and the distance between them,and proposed a population-based gray wolf algorithm to solve the IM problem.Liet al.[13]proposed a discrete crow optimization metaheuristic algorithm to efficiently solve the IM problem.This type of algorithm has a significant improvement in running time when compared with the greedy strategy-based approach.There is also a substantial improvement in the solution accuracy when compared to the centrality-based methods.However, the existing metaheuristic algorithms have some limitations because they may fall into another local optimum when they try to get rid of the local optimum.With this in mind, we develop a discrete twostage metaheuristic optimization(DTMO)algorithm combining QPSO and L′evy flight to efficiently identify the influential nodes in the network.The main contributions of this paper are as follows:
A new two-stage metaheuristic optimization algorithm framework was formulated to solve the IM problem.
(i) The evolution rules of the quantum-behaved particle swarm optimization algorithm were modified and a discrete quantum-behaved particle swarm optimization(DQPSO)algorithm with nonlinearly decreasing randomized crossover operation was developed.
(ii) A discrete L′evy flight (DLF) algorithm with automatic candidate pool selection based on greedy strategy was presented to enhance the performance of the DQPSO.
(iii) A new method for population diversity calculation was designed and a novel algorithmic transformation strategy was introduced using this method.
(iv) Our method was compared with other well-known methods on six real-world social networks.The experiments showed that our method can obtain comparable effects to the algorithms based on greedy strategy but with low time complexity.
The rest of this paper is organized as follows.Section 2 reviews and discusses the related work.The problem description,the fitness assessment function,and the propagation model are given in Section 3.Section 4 presents the original QPSO and L′evy algorithms and describes our proposed framework in detail.The experimental results and analysis are given in Section 5.Finally, this study is summarized and future research directions are proposed in Section 6.
2.Related work
The IM problem was first proposed from a network perspective by Domingos and Richardson,[5]where the authors argued that consumers and the individuals around them are interconnected and have an interacting influence, which was modeled through Markov random field theory.Kempeet al.[6]transformed the IM problem into a combinatorial optimization problem.They adopted the Monte Carlo simulation mechanism to evaluate the influence of candidate nodes and introduced a greedy algorithm that was based on a hill-climbing search strategy to find the influential nodes.To reduce the expensive computational cost that arose from the Monte Carlo simulations,Leskovecet al.[14]developed an improved greedy algorithm that was scalable to large-scale social networks.Their experiments showed that it is 700 times faster than the simple greedy algorithm, while the results are nearly optimal.Subsequently, Goyalet al.[15]proposed a superior version called CELF++, which is 35%–55% faster than CELF.Following this seminal work, Zhanget al.[16]introduced a residual-based algorithm RCELF that can achieve good time efficiency, low memory consumption, and approximate quality of the results.Compared with the original greedy algorithm, the improved greedy algorithm has a certain degree of improvement in terms of time cost.However,some algorithms need to record the states during propagation to reduce the number of Monte Carlo simulations.Meanwhile,some algorithms increase the memory consumption,which means that they cannot be scaled to real large-scale social networks.
Several heuristic algorithms have been put forward to tackle IM variations.Chenet al.[17]gave a more accurate discount value to the neighbors of the nodes selected as seeds and proposed the DegreeDiscount under the IC model with small propagation probability.Their experiments showed that the fine-tuned heuristic can provide a truly scalable solution to the IM problem with satisfactory propagation range and greater efficiency.Zareieet al.[18]proposed a special hierarchical measure to provide sufficient information about the topological position of the nodes,which ranks the influence of nodes more accurately than other state-of-the-art measures.Wanget al.[19]introduced a new metric, which they called node key degree,to measure the importance of nodes,and proposed the IT¨O algorithm to balance the conflict between exploration and exploitation.More recently, considering the dynamic nature and local aggregation factors on diffusion,Liet al.[20]adopted various entropy calculations to obtain the cohesion between neighboring nodes and then identify whether the node has the ability to become a propagable pioneer of other nodes.Menget al.[21]combined H-index,K-shell iteration factor,and clustering coefficient to attach weights to connected edges,which were in turn combined with the neighborhood, position and topology of nodes in the network to identify influential nodes.Liet al.[22]combined an improved gravity model with the community detection method to identify influence propagators in the network by finding bridge nodes in the network’s topology.Compared with traditional centrality methods, the methods combining the node characteristics can achieve a certain degree of improvement in accuracy.However,there is also a high time complexity,which makes it difficult to apply these methods to large-scale networks.In addition, some methods only measure the local structure of the network without diversity,and therefore lack solution stability when dealing with the IM problem.
Some recent research interest has focused on the use of metaheuristic algorithms,broadly referring to the construction of low computational cost influence evaluating models and the utilization of appropriate evolutionary optimization strategies to view the IM problem as a fitness optimization problem.Jianget al.[23]were the first to use the fitness evaluation function, named expected diffusion value (EDV), as an influence evaluation measurement and proposed a simulated annealing algorithm to optimize EDV to identify a set of influential seed nodes.Their experimental results showed that the proposed algorithm runs 2–3 orders of magnitude faster than the state-of-the-art greedy algorithm,while improving the optimal solution accuracy.Gonget al.[24]proposed a discrete particle swarm optimization algorithm to map candidate seeds to particles in the population and established a novel evaluation function called local influence estimation (LIE), which can be evaluated more accurately under the IC model with lower time complexity.A metaheuristic discrete bat algorithm based on the collective intelligence of individual bats from the population was proposed by Tanget al.[25]This algorithm combines the evolutionary rules of the original bat algorithm and designs a seed node candidate pool to enhance the search capability of the algorithm, and finally achieves satisfactory experimental results.By analyzing the efficiency of the greedy algorithm,Cuiet al.[26]proposed a degree-descending search strategy and developed a more efficient evolutionary algorithm,named degree-descending search evolution(DDSE),through the operations of mutation,crossover,and greedy selection.Singhet al.[27]extended EDV to a two-hop area to realize a more accurate evaluation of seed nodes and proposed a variant of discrete particle swarm optimization(DPSO)based on the mechanism of learning automata.To maximize the distance between the seed nodes and ensure that different parts of the network are reached,Zareieet al.[12]solved the IM problem by optimizing the influence of nodes and the distance between them via the gray wolf optimization algorithm, which performed well in experimental results and had lower computational cost.Wanget al.[28]developed an influence evaluation model based on the total valuation and valuation differences of neighboring nodes.The authors developed an evolutionary strategy with local crossover and variation on natural moth evolutionary rules.Their experiments showed that the method is effective and robust in dealing with the IM problem.After conducting extensive experiments, Weskidaet al.[29]showed computationally that evolutionary algorithms not only overcome the limitations of greedy algorithms but also have several advantages, such as the transferability of their parameters.However,a reasonable discrete evolutionary mechanism can provide a balanced trade-off in terms of solution accuracy,time consumption,and even memory management.Therefore,the design of more effective influence evaluation mechanisms and more reasonable evolution mechanisms deserves further discussion.
Quantum-behaved particle swarm optimization, as a swarm intelligence algorithm, was proposed by Sunet al.[30]from a quantum mechanical perspective by combining some features of the original particle swarm optimization(PSO)algorithm.Due to its efficiency and robustness, this algorithm has recently been applied to solve problems in various fields.For example, a hybrid inversion method based on the quantum particle swarm optimization method was introduced to solve the electromagnetic inverse problem by Yanget al.[31]Bajajet al.[32]proposed a discrete quantitative particle swarm optimization to improve the efficiency of test case prioritization.There are many other studies and applications of QPSO,such as path planning and the design of mobile robots in the workspace,[33]the constrained portfolio selection problem,[34]and the network clustering problem.[35]The results of these studies show that the QPSO algorithm provides strong robustness and solution efficiency thanks to its excellent evolutionary rules.
QPSO has attracted the attention of many researchers due to the simplicity of the evolution equation,few control parameters, and fast convergence, but it also suffers from problems such as premature convergence.As a random wandering strategy,L′evy flight is mainly adopted by combinatorial optimization algorithms to effectively solve intractable optimization problems, such as the green scheduling problem of the flexible manufacturing cell.[36]However,the use of combinatorial algorithms based on QPSO and L′evy flight for the IM problem has not yet been reported in the literature.Therefore, exploring reasonable evolutionary mechanisms based on QPSO and L′evy flight to effectively identify influential nodes is worth further investigation.
3.Preliminary information
3.1.Influence maximization
In the study of IM,a social network can be abstracted as a graphG=(V,E),whereV={v1,v2,...,vn}is the set of vertices, representing the individuals or organizations in the social network, andE={e1,e2,...,em}is the set of connected edges, indicating the existence of connections and cooperation between individuals or organizations in the social network.Note thatnandmdenote the number of vertices and the number of connected edges in the network,respectively.
For a given graphG,a set ofk(k ?n)influential nodes are selected and ignited.The number of nodes activated by the seed set in the graph is expected to be maximized under a specific propagation model.This problem can be formalized as
whereσ(·) is a measure of influence spread,Srepresents a candidate seed set withknodes andS?denotes the optimal seed set that maximizes the influence spread.
3.2.Influence estimation function
In the IM problem, the influence evaluation methods are divided into two main categories: (i) in the first category, a Monte Carlo simulation evaluates the propagation outcomes of the influential nodes;and(ii)in the second category,information based on the neighborhood structure characteristics of the nodes is utilized to estimate the diffusion effect of the seed nodes.
Although the Monte Carlo simulation method can achieve high accuracy, it is not well satisfied with practical scenarios due to its tremendous computational complexity.Therefore,to reduce computational cost, Jianget al.[23]proposed an influence evaluation function based on the direct adjacent neighbors of its corresponding seed nodes.Inspired by the principle of two-degree theory on influence spreading,[37]Gonget al.[24]proposed a LIE function, which approximates the expected influence spread based on the two-hop neighbors area of the influential nodes,

3.3.Influence propagation model
Currently, there are three widely spreading models for simulating influence propagation in the IM problem: the IC model,the LT model,and the weighted cascade model.Based on the influence estimator, we employ the classical IC model to simulate the spread of influence in given networks.In the IC model, nodes have two states: active and inactive.The node can only be converted from the inactive state to the active state during the propagation process, and vice versa.In the diffusion process,when a node is activated at timet,it has a single chance at timet+1 to activate its direct inactive neighbors with probabilityp.When a new node is activated, it repeats the previous step until no new node is activated,the propagation ends,and all nodes in the active state are returned.
4.Algorithm
4.1.Quantum-behaved particle swarm optimization
PSO, one of the most widely used swarm intelligence algorithms, was originally proposed by Kennedy and Eberhart.[38]PSO is often used to solve optimization problems due to its effectiveness and robustness.The original updating rules for PSO can be described as follows:
wherewis the inertia weight,c1is the individual learning factor,c2is the social learning factor, andr1andr2are random numbers drawn uniformly from[0,1].Xi=(x1,x2,...,xd)andVi=(v1,v2,...,vd)represent the position vector of theith particle in thedth dimension and its corresponding velocity vector,respectively.Pbestidenotes the historical best position of particleiand Gbest is defined as the best position in the whole population.More specifically,the first partwVtiin Eq.(4)reflects the effect of the particle’s velocity at timeton its new velocity at timet+1,and the second partc1r1(Pbesti?Xti)and the third partc2r2(Gbest?Xti) imply that the particle learns information from its corresponding historical optimal position and global optimal position of the population,respectively.
In recent years, many strategies have been proposed to enhance the performance of PSO, such as L′evy flight,[39]multi-swarm cooperative approach,[40]and fitness landscape features.[41]Inspired by quantum mechanics theory and trajectory analysis,[42]the ideology of quantum parallel mechanics is introduced into the framework of PSO to improve the performance of the algorithm,termed the quantum particle swarm optimisation algorithm,which outperforms traditional PSO in terms of exploration capability but with fewer control parameters.In QPSO,the position of theith particle is updated according to the following equations:
where Pbestiand Gbest denote the historical best position and the global best position of theith particle, respectively.Piis defined as a local attractor.According to Eq.(6), it can be seen that the local attractorPiis located in a hyper-rectangle with Pbestiand Gbest as vertices.?anduare random numbers in the interval(0,1),βis a contraction-expansion factor,and mbest is the average of the best positions of all particles.Ifu <0.5, then the minus symbol “?” is selected in Eq.(7),otherwise the plus sign“+”will be selected.The framework of QPSO is given in Algorithm 1.

Algorithm 1 The framework of QPSO.Initialize each particle’s position,Pbest,Gbest while T <Tmax do for each particle do Calculate local attractor Pi using Eq.(6)Compute particle’s position using Eq.(7)Update Pbest and Gbest end for end while Return the best position Gbest.
4.2.L′evy flight
In nature,most animals generally combine frequent shortdistance wandering with occasional long-distance travel when foraging food.As a random walk process,L′evy flight mainly consists of frequent local exploitation and occasional global exploration of the search space.The application of this mechanism to swarm-based intelligence algorithms can enhance the global search capability of the metaheuristics and prevent them from falling into premature convergence.By combining the characteristics of L′evy flight, some researchers have introduced hybrid swarm intelligence optimization algorithms[36]with promising results.The following are the rules to calculate the inherent step lengths of L′evy flight:
wherelrepresents the random step.For the parameter setting,1<m ≤3,andμ~N(0,σ2μ),υ~N(0,σ2υ).υandυare random numbers obeying Gaussian distribution,whileσμandσυsatisfy the following equations:
where Γ(·)denotes Gamma function.Figure 1 shows the trajectory of an individual wandering randomly in the search space under the L′evy flight mechanism.
Fig.1.The trajectory of an individual after flying 1000 steps under theL′evy flight in two dimensions.
4.3.Proposed algorithm
The whole framework of the proposed algorithm for IM is outlined in Algorithm 2.The algorithm is divided into three main stages: (i) initialize the particles in the population; (ii)update the positions of the particles in the population according to the rules of DQPSO;and(iii)apply the L′evy flight strategy on the Gbest and finally output the optimal solution.

Algorithm 2 The framework of the proposed algorithm.Input Graph G=(V,E),size of particle swarm n,size of seed set k,number of iterations Tmax and the contraction-expansion coefficient β1 and β2.Initialize particle position vectors X and Pbest Initialize historical diversity value HDV ←0 Initialize stages of algorithm evolution Stage ←1 Initialize iterator T ←0 Compute the shortest path length matrix M for graph G Compute fitness(X)and fitness(Pbest)Select out the initial global best position vector Gbest while T <Tmax do Update the stage of the evolution Stage and identify the algorithm to be selected Algorithm switch Algorithm do case Algorithm==“DQPSO”do Apply the DQPSO algorithm to update X Update Pbest and Gbest end case case Algorithm==“DLF”do Apply the DLF algorithm to update Gbest end case end switch T ←T+1 end while Output Output the best position Gbest as the seed set S.
4.3.1.Initialization
During the initialization phase,a degree-based initialization strategy similar to that of DPSO is employed.First, all particles in the population select the topknodes with the greatest degree in the graphG.At the same time,to guarantee the diversity of the population, a random replacement operation on the nodes in each particle is performed,i.e.,when the random value is greater than 0.5,the corresponding node will be replaced by any node in the graphGthat has not been selected as a candidate node in that particle.The same approach is utilized when initializing Pbest.The detailed initialization procedure is given in Algorithm 3.

Algorithm 3 Initialization.Input Graph G=(V,E),the size of particle swarm n,size of seed set k.for each i ≤n do Xi ←degree(G,k)for each element xij ∈Xi do if random>0.5 then xij ←replace(xij,N)end if end for end for Output The initial position vector X.
4.3.2.Discrete quantum-behaved particle swarm optimization algorithm
The original QPSO algorithm is only applicable to solve optimization problems with continuous space.Therefore, the update rules are redesigned in discrete form to solve the IM problem.The new evolutionary mechanism of DQPSO is defined as
whereuis a random value between 1/e and 1,Xtiis the position vector of theith particle at iterationt,βrepresents contraction-expansion coefficient, andβln(1/u) is redefined as the crossover probability, as described by the following equation:
forβ1=1,β2=0.5.Tmaxrepresents the maximum number of iterations.From Eqs.(10) and (11), it is obvious thatβgenerally varies nonlinearly from 1 to 0.Whenβreaches a large value in the first few steps, the crossover ability of the particles becomes stronger,which indicates that the particles have stronger exploration ability.In the later stages, the crossover ability of the particles gradually becomes weaker and ostensibly the particles gradually tend to converge.However, since ln(1/u)is a random value,there is also a lower probability of obtaining a stronger crossover ability, which to some extent increases the diversity of the population.
In Eq.(10),Ptiis given by
where?is a random value drawn from [0,1],k?is rounded upward to determine the number of nodes to be randomly selected in Gbest or Pbest, and then the selected nodes are merged to obtain the local attractorPi.When selecting nodes at random, it is important to ensure that the selected nodes cannot be duplicated.The specific operation is shown in Fig.2, assuming that Pbesti={1,5,10,17,20}, Gbest={3,5,11,14,19},k=5,?=0.36,thenk?=2;therefore,two nodes in Pbset and three nodes in Gbest need to be taken for combination.

Fig.2.Illustration of how to obtain local attractor Pi.The blue boxes represent the nodes to be randomly selected.
In the original QPSO algorithm, mbest is the average of the best positions of all of the particles.When mbest takes this case, it does not guide the particles very well, and therefore mbest is redefined as the average of the optimal positions of the top three particles.First,the top three particles are divided into two portions,the first portion includes the common nodes belonging to the three particles,and the second portion maintains the remaining nodes in the particles.All of the nodes in the first portion are then selected into Mbest.Finally, the nodes are randomly selected from the second component until there areknodes in the Mbest.A detailed illustration of this operator is shown in Fig.3.It is assumed that the top three historical optimal positions are Pbest1={1,3,4,7,11},Pbest2={1,4,6,8,10},Pbest3={1,5,4,8,11},the identical nodes are then{1,4},and the remaining nodes are{3,10,11,6,8,7,5},finally Mbest={1,4,8,5,10}is obtained by the restructuring mechanism.
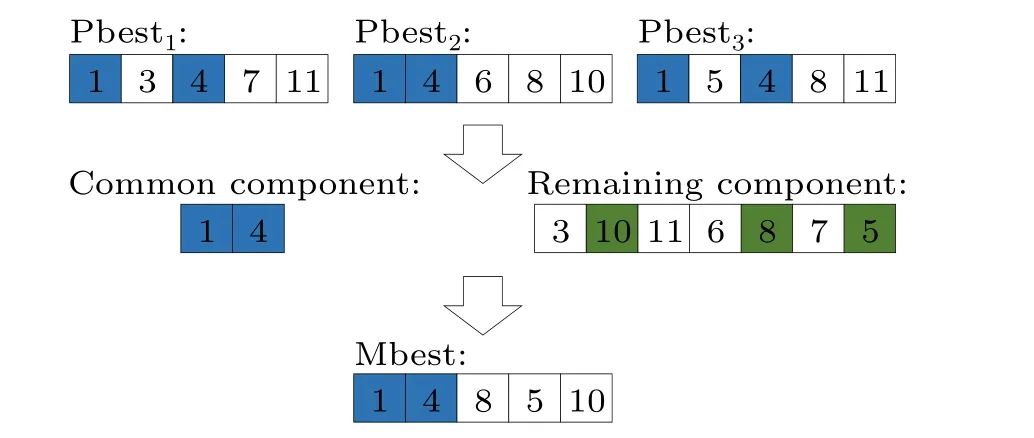
Fig.3.Illustration of the calculation of Mbest.The blue boxes represent common nodes belonging to all three particles and the green boxes represent randomly selected nodes.
The operator∩in Eq.(10)is a logical operator that is defined as a similar intersection operation to determine whether there are different elements in Mbest andXi.When a node inXiis a unique node to Mbest, the crossover probabilityβln(1/u)is calculated.Ifβln(1/u)is greater than a random value drawn from[0,1],then a node in Mbest that is not inXiis selected for the intersection exchange operation;otherwise,no operation is performed on that node.The⊕operation is the process of greedy search of the local attractorPsubject to the new particle position vectorXiobtained by the crossover operation.In this process, the nodes in the local attractorPithat are identical to those inXiare removed and then treated as a pool of candidate nodes.For each node inXi,an arbitrary node from the candidate node pool is selected to replace it.Meanwhile, the selected node is removed from the candidate node pool.When the position of the node after being replaced is better than the previous position, then any node from the candidate node pool continues to be selected for replacement;otherwise, the same operation is performed for the next node inXi.It should be noted that the operation is terminated when there is no node in the candidate pool.The framework of the DQPSO algorithm for IM is presented in Algorithm 4.

Algorithm 4 DQPSO algorithm framework.Input Particle position vectors X,the size of particle swarm n,size of seed set k,particle local attractor position vectors P attr,iterator T,the mean of the best position of the top three particles Mbest,the number of iterations Tmax,and the contraction-expansion coefficient β1 and β2.for each i ≤n do if Xij /∈M best do Compute the probability of mutation pmu if pmu >rand do Xi ←replace(Xi j,Mbest)end if end if end for for each i ≤n do candidate pool= /0 if P attrij /∈Xi do cand pool ←cand pool∪P attrij end if X'i ←Xi for each j ≤k do if cand pool== /0 do break end if Flag ←False while Flag==False do if cand pool== /0 do break end if X'ij ←replace(X'i j,cand pool)if fitness(X'i)>fitness(Xi)do Xij ←X'ij else do Flag ←True end if end while X'ij ←Xij end for Xi ←X'i end for Output Output particle position vectors X.
4.3.3.Algorithm transformation
To avoid the DQPSO algorithm converging swiftly to a suboptimal global solution,a metric to assess the diversity of the population is conceived.The diversity metric can be formulated as follows:
wherenis the size of the particle swarm,kis the size of the seed set, and the∩operation returns the number of identical nodes in the two position vectors.It can be seen from Eq.(13)that the diversity value becomes larger and the diversity of the population decreases with the evolution of the algorithm.When the diversity value of the population is less than its historical,it indicates that the population has converged to a stagnation.In this case,the algorithm will perform the second stage,i.e.,discrete L′evy flight,to identify a more optimal position.The framework of updating stage and identifying algorithm is given in Algorithm 5.

Algorithm 5 Update Stage and identify Algorithm.Input.Particle position vectors X,particle best position vectors Pbest,evolution stage Stage,and historical diversity value HDV.switch Stage do case Stage==1 do Compute Mbest Compute P attr Compute the current diversity value CDV if CDV?HDV >0 do HDV=CDV Algorithm=“DQPSO”end if else do Stage=2 Algorithm=“DLF”end case case Stage==2 do Algorithm=“DLF”end case end switch Output Output the stage of the evolution Stage and identify the algorithm to be selected Algorithm.
4.3.4.Discrete L′evy flight
The original L′evy flight is not available to solve discrete IM problem directly.Therefore, a discrete L′evy flight mechanism based on the shortest path length of the network is proposed.
Since the previous stage evolves through the DQPSO algorithm, the population tends to remain in an optimal state.Therefore,there is no need to perform discrete L′evy flight for all of the particles in the population but only for the Gbest.The shortest path length matrixMof graphGis first obtained in the initialization phase,and then L′evy flight step lengthlis derived from Eq.(7)and rounded upward.During the searching process, each node in Gbest will be replaced with a randomly selected node from the candidate pool, which is composed of nodes in Gbest with the same shortest path length in the network and the same flight step lengthlbut not the same as in Gbest.When the step flight lengthlis greater than the maximum shortest path length of that node in the network,the flight lengthltakes the maximum shortest path length of that node in the network.The detailed replacement process is the same as the⊕operation mentioned earlier.The framework of the DLF algorithm for IM is described in Algorithm 6.

Algorithm 6 DLF framework of algorithm.Input The best position Gbest and the shortest path length matrix M.Gbest'←Gbest for each i ≤k do compute the step size of the L′evy flight l cand pool ←M(Gbest(i),l)if cand pool== /0 do break end if Flag ←False while Flag==False do if cand pool== /0 do break end if Gbest'i ←replace(Gbest'i,cand pool)if fitness(Gbest')>fitness(Gbest)do Gbest ←Gbest'else do Flag ←True end if end while Gbest'←Gbest end for Output Output the best position Gbest'.
5.Experiment and analysis
5.1.Network data sets and baselines
To verify the performance of the proposed DTMO on the IM problem,we conducted extensive experiments on six realworld networks that were collected from NR with the topological characteristics shown in Table 1,where〈k〉represents the average node degree,Cis the average clustering coefficient,andACrepresents the assortativity coefficient.Figure 4 shows the node degree distribution of the networks.The results of influence spread are compared with several state-of-the-art methods, including the degree centrality (DC) based on the network topology, discrete moth-flame optimization (DMFO),[28]DDSE,[26]DPSO,[24]learning automatabased discrete particle swarm optimization(LAPSO),[27]costeffective lazy forward (CELF)[14]algorithm based on greedy strategy,and layered gravity bridge algorithm(LGB).[22]
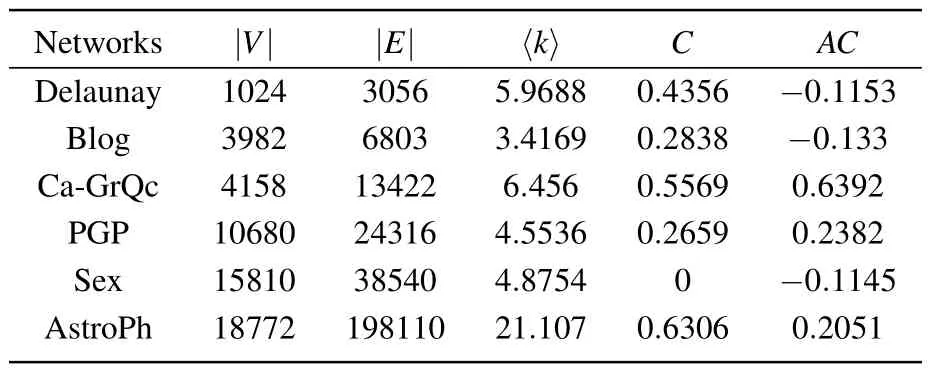
Table 1.Topological characteristics of the six social networks.
5.2.Parameter configuration
To test the scalability of the algorithm, the size of the seed setkwas set to 5, 10, 15, 20, 25, 30, 35, 40, 45, and 50, respectively, the maximum iterationsTmaxwere 100 and the population size was chosen as 100.In DMFO,the amplification factor was set toc=4, the mutation probability was 0.1,and the coefficientωwas 0.8.In DPSO and LAPSO,the learning factors were set toc1=c2=2,the inertia weight was 0.8,and additionally the values of the reward and punishment parameters were set toar=bp=0.6 in LAPSO.In DDSE,the probabilities of mutation, crossover, and diversity operations were set to 0.1, 0.4, and 0.6, respectively.The number of Monte Carlo simulations for CELF was set to 10000.In addition, 1000 Monte Carlo simulations were performed on the optimal set of seeds obtained by all of the other algorithms to obtain the average spreading coverage under the IC model with propagation probabilityp=0.01.
5.3.Comparison of the LIE evaluation
To validate that DQPSO and DLF play a desirable effect on their respective phases, we compared the fitness values of the obtained optimal seed sets of DTMO,DQPSO,and DPSO.Figure 5 shows the average LIE of different seed sizekon the six networks.
In the Delaunay network,as shown in Fig.5(a),all three algorithms perform competitive results over the entire interval, and a detail view atk=50 shows that DTMO gains a better marginal gain.In Blog and CaGrQc, the algorithms gradually show visible gaps as the seed numberkincreases and the gap gradually becomes more evident as the network’s scale increases.In Figs.5(d) and 5(e), it can be seen that DPSO is highly prone to suboptimal solutions, while DTMO and DQPSO have no evident instability, which indicates that the proposed algorithm has strong robustness.It is worth mentioning that, except for the Ca-GrQc network, the fitness values of DTMO and DQPSO are not significantly different throughout the interval ofk.In contrast, in Fig.5(c), there is a significant gap between the algorithm DTMO and DQPSO atk=50.This indicates that the random wandering strategy in the second stage of the algorithm compensates for the deficiency of the DQPSO algorithm falling into premature convergence.Overall,both the two-stage DTMO and the separate DQPSO achieved satisfactory results in all six networks.
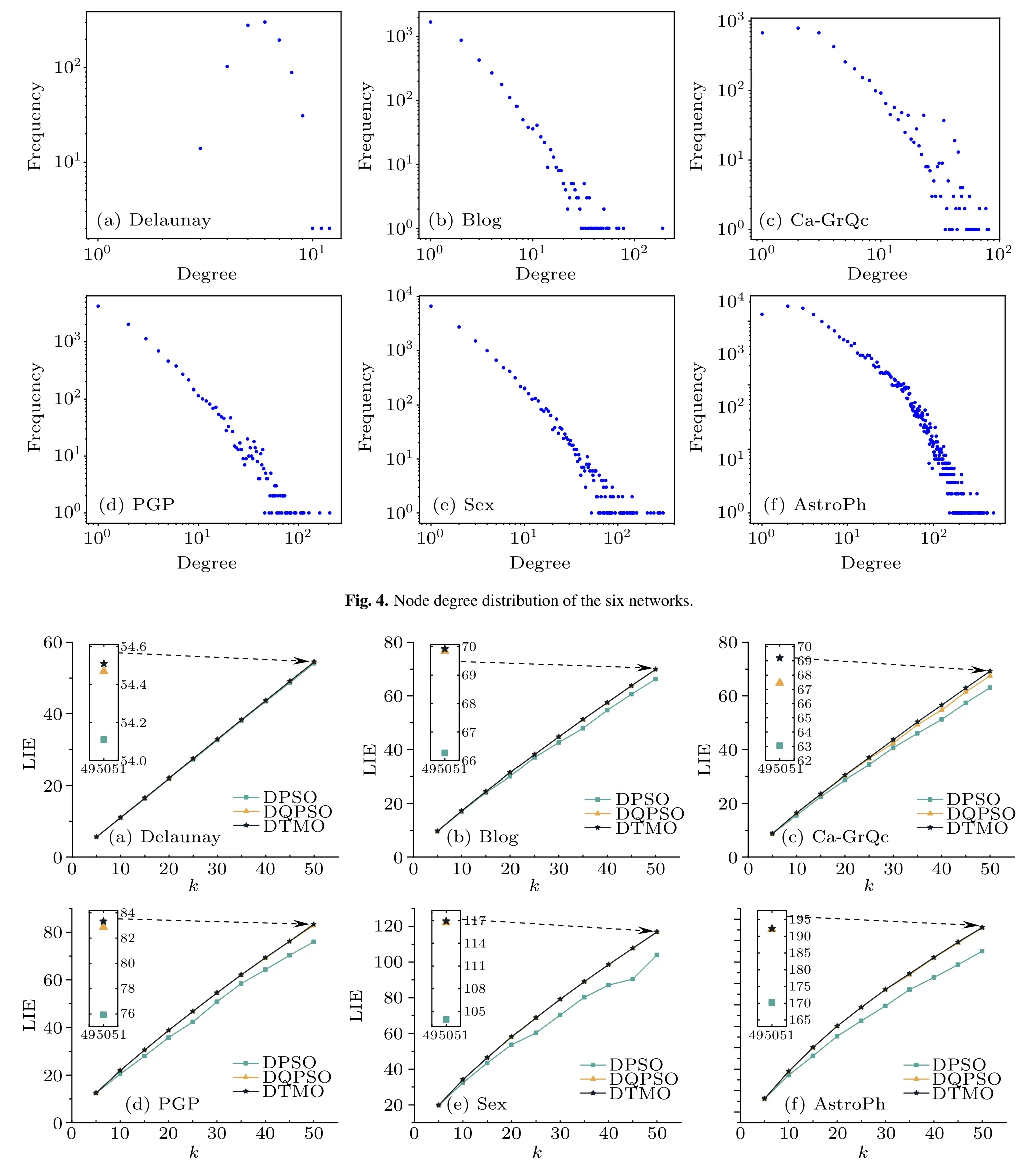
Fig.5.Comparison of LIE optimization of the three algorithms in the six social networks at different seed size k under p=0.01.
5.4.Performance comparison of the typical algorithms
To further validate the ability of the proposed DTMO algorithm to solve the IM problem,six state-of-the-art methods were selected to compare with DTMO in terms of the number of nodes activated in the network under the IC model.As shown in Fig.6, the spread size achieved by DTMO shows that it can return satisfactory propagation in the six networks.Moreover,it can be seen that DTMO has the most stable performance in different scenarios.
More specially, in the Delaunay network, it can be observed that the algorithms achieve similar influence spread throughout the range of 5≤k ≤50,and the proposed DTMO algorithm achieves the best result.In the Blog network shown in Fig.6(b), comparable results are obtained for all six algorithms except DMFO on the interval of 15≤k ≤25.There is a significant decline in the effectiveness of DPSO whenk ≥30.Atk=50,DDSE outperforms the others by a significant margin,while DTMO comes in a close second.
Figure 6(c)shows that CELF,DMFO,LGB,and DTMO can maintain good momentum whenk ≥15.LAPSO and LGB algorithms achieve similar performance over the entire interval,while the other algorithms show different levels of performance degradation.Atk=45 andk=50, both DTMO and DMFO outperformed the CELF and achieved the best influence spread.In addition,DTMO and DMFO achieved one optimal result each,indicating that both DTMO and DMFO have strong competitiveness in this network.Figure 6(d)shows that the ranking of all algorithms remains essentially constant over the entire range of seed size, with CELF and DTMO achieving comparable performance, and LAPSO coming in second.It should be noted that in Figs.6(c)and 6(d),both DDSE and DC showed lower efficiency.This is probably due to the fact that in both networks only the one-hop neighbors of the candidate nodes are evaluated,which leads to the problem of overlapped influence propagation in the propagation process.
In Fig.6(e), similar experimental results were obtained by LAPSO,CELF,DC,LGB,and DTMO.More specifically,LAPSO performed the best in the interval of 15≤k ≤45,while CELF and DTMO were entangled with each other in the influence size.Atk=50,DTMO,LGB,and LAPSO obtained the same results.It is worth mentioning that the topology of the network is a star structure, so DC can achieve satisfactory results.Meanwhile,DC degenerated atk=50 because it suffers from the influence overlap problem as the number of selected nodes increases.In the AstroPh network of Fig.6(f),DMFO and DTMO have achieved relatively high performance but were slightly inferior to CELF.
In summary, DTMO achieved comparable or even better results than CELF in most cases, indicating that DTMO can effectively solve the IM problem.DC and DDSE performed poorly in some networks because they only evaluated the one-hop neighbors of the nodes, resulting in inaccurate evaluation of influence.Although DPSO was more accurate in evaluating candidate nodes,the algorithm tended to be stagnant because its local search strategy easily returns the local optimum.LGB offers a dramatic improvement in influence dissemination when compared to traditional centrality-based approaches.LAPSO and DMFO achieved desirable results in some scenarios.This indicates that the improvement of PSO and the searching strategy in DMFO are very effective, and the respective evaluation functions can accurately evaluate the influence of the nodes.
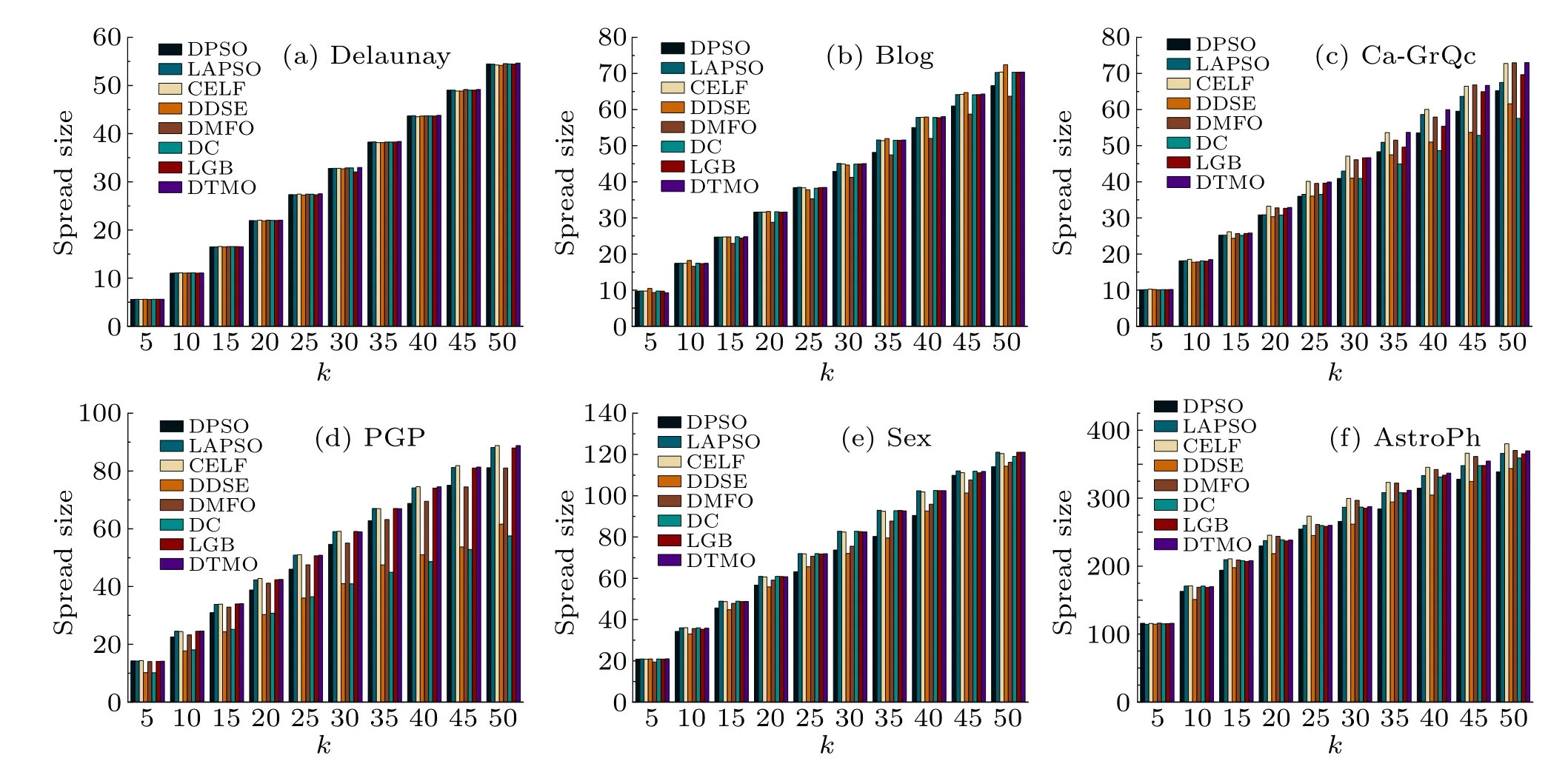
Fig.6.Comparison of the influence spread size of DTMO against six other algorithms under the IC model(p=0.01)on the six networks.
5.5.Statistical tests
To demonstrate the effectiveness of the proposed DTMO algorithm in identifying influence spreaders,a statistical analysis was employed to test the statistical significance of the performance differences of the six algorithms on the six networks,the results are reported in Table 2.In all six networks,the scenarios ofk=10,20,30,40, and 50 were chosen as independent problems,and hypotheses were tested for each scenario.Wilcoxon rank sum test at the confidence level of 0.05 was conducted to show the superior performance of DTMO over the other six algorithms.
From the statistical results, it can be seen that the influence propagation obtained by the DTMO algorithm is better than DPSO algorithm on the whole selected interval.DDSE, DMFO, DC, and LGB have similar performance,while LAPSO has slightly better performance.At the same time, it can give a similar performance guarantee when compared with CELF.
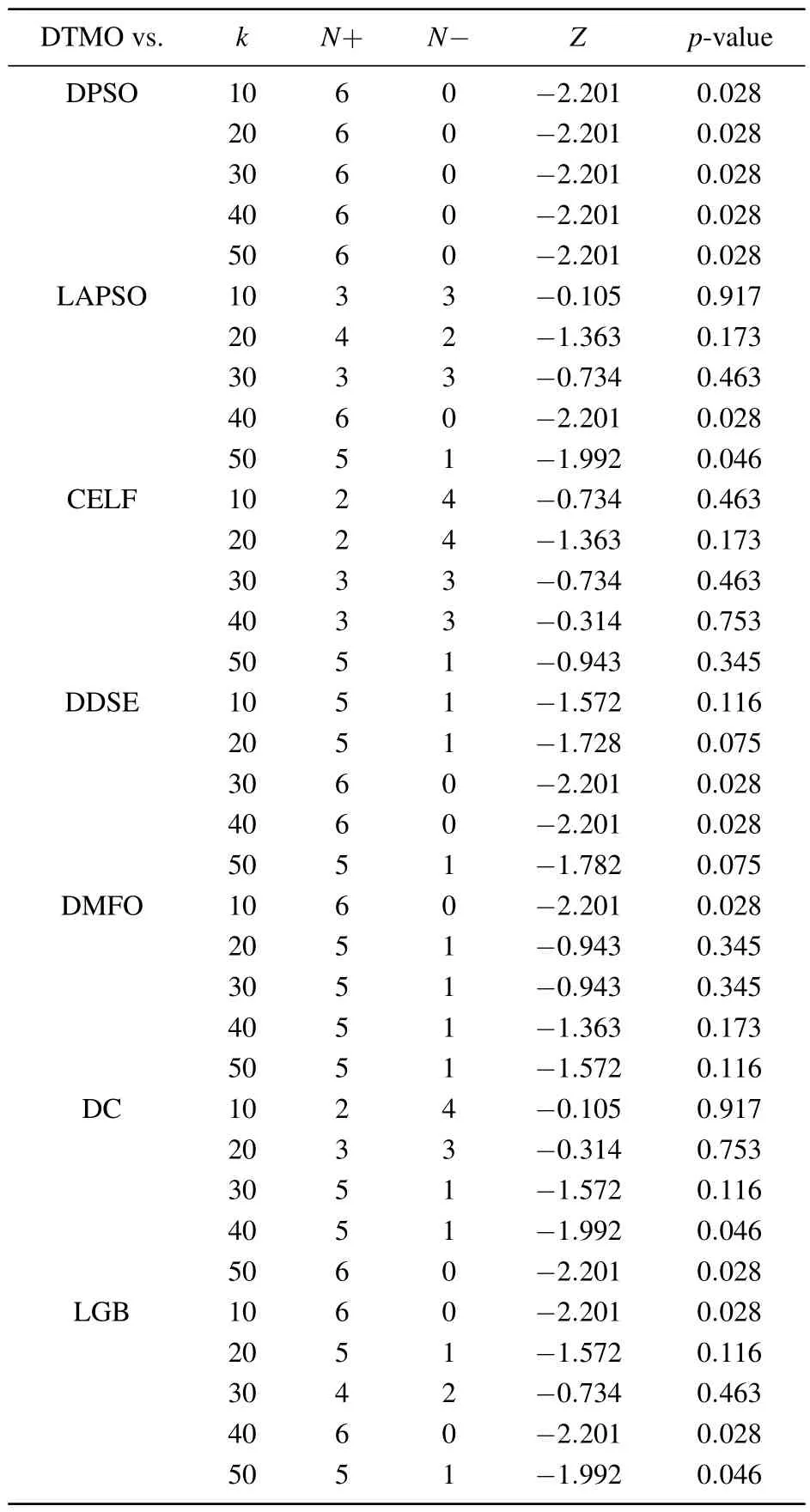
Table 2.Statistical results of the Wilcoxon test for the seven algorithms at α =0.05.
6.Conclusion
In this paper,a DTMO algorithm combining QPSO with L′evy is proposed to solve the IM problem.In the first stage of the algorithm,the evolutionary rules of the redefined DQPSO are used to update the particle positions to make the particles fly to a more optimal position.At the same time, population diversity is defined to determine whether the particles in the population converge to the optimal.When the particles in the population are in convergence, the second stage of the algorithm is performed to obtain the global optimal solution by updating the optimal positions of the particles in the population using the redesigned DLF mechanism.Finally, experiments with other well-known algorithms on six real networks show that the proposed algorithm obtains comparable or even slightly superior results to CELF but with less computational cost and obtains significantly better results when compared to the other algorithms.
Acknowledgments
Project supported by the Zhejiang Provincial Natural Science Foundation (Grant No.LQ20F020011), the Gansu Provincial Foundation for Distinguished Young Scholars(Grant No.23JRRA766),the National Natural Science Foundation of China (Grant No.62162040), and the National Key Research and Development Program of China (Grant No.2020YFB1713600).
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals

