A Game Theoretic Approach for a Minimal Secure Dominating Set
Xiuyang Chen, Changbing Tang,,, and Zhao Zhang
Abstract—The secure dominating set (SDS), a variant of the dominating set, is an important combinatorial structure used in wireless networks.In this paper, we apply algorithmic game theory to study the minimum secure dominating set (MinSDS) problem in a multi-agent system.We design a game framework for SDS and show that every Nash equilibrium (NE) is a minimal SDS, which is also a Pareto-optimal solution.We prove that the proposed game is an exact potential game, and thus NE exists,and design a polynomial-time distributed local algorithm which converges to an NE in O(n) rounds of interactions.Extensive experiments are done to test the performance of our algorithm,and some interesting phenomena are witnessed.
I.INTRODUCTION
WITH the rapid progress of wireless network technology,some distributed network systems such as multi-agent systems, sensor networks, and wireless ad hoc networks have become more and more popular for network monitoring which only requires little intervention from people.To save cost, it is desirable to use small number of intelligent devices to collect information from the whole system.Such a consideration leads to the minimum dominating set (MinDS) problem [1].
Note that in a MinDS problem, each sensor is only responsible for detecting security issues of the system, and is not endowed with the power to handle them.This limits the scope of application of dominating sets.For example, in a museum,each pavilion is viewed as a vertex of a graph, and the corridors between the pavilions form the edge set of the graph.A guard in pavilionviis responsible for monitoring the surrounding pavilionsN[vi], whereN[vi] is the closed neighbor set ofvi.If every pavilion could be monitored, then those pavilions with guards form a dominating set.If a problem occurs in a guarded pavilion, then the guard in the corresponding pavilion can deal with the issue.If a problem occurs in an unguarded pavilion, then a nearby guard could move to deal with the issue.At the same time, it is expected that all pavilions remain to be monitored after movement.This leads to the minimum secure dominating set (MinSDS) problem.In addition to the above scenario, SDS problems are also applied in the context of the protection system, network security system,military strategy analysis, etc.[1]–[4].
The concept of SDS was first introduced by Cockayneet al.[5] in 2005.Burgeret al.[6] designed two exponential-time algorithms for the MinSDS problem in general graphs.It is known that the MinSDS problem is NP-hard.In fact, Boumediene Merouane and Chellali [7] proved that the MinSDS problem is NP-hard even when restricted to bipartite graphs and split graphs.Therefore, many people attempted to solve the MinSDS problem with special classes of graphs [4],[8]–[15].These algorithms are centralized.Note that centralized algorithms are vulnerable to external attacks.Damage to the center may lead to a breakdown of the whole system.This observation motivates us to seek distributed algorithms for the MinSDS problem.
A distributed algorithm can effectively reduce the damage of attacks, especially in multi-agent systems, in which each node is an autonomous agent and can determine its strategy for the next step based on currently collected information(which is often local since an agent might not be as powerful as a center).Such an autonomy eliminates the dependence on a center, and greatly improves anti-attack capability.Note that individual benefits and social welfare are often conflicting.Thus, a disadvantage resulting from such autonomy is that a self-organized algorithm take a longer time to run, and may fail to get satisfactory solutions.
Using game theory can effectively cope with the above disadvantages, and the hypothetical definition of a player is exactly what we expect from an agent: rational, intelligent,and selfish.Game theory has the advantage whereby providing interaction frameworks (game design) and specific local rules (distributed methods), a satisfactory collective behavior may be theoretically guaranteed through competition and cooperation among individuals.For studies of game theory in wireless and communication networks, readers may refer to the monograph [16] and references therein.
Compared with the large quantities of approximation algorithms for the MinDS problem and its variants [17], studies on the domination problems using game theory are not as common.Yen and Chen [18] designed a multi-domination game and proved that every Nash equilibrium (NE) of the game is a minimal multi-dominating set, and is also a Pareto optimal solution.Based on the game, a distributed algorithm was designed.Note that the algorithm uses a central daemon which allows only one process at a time.Later, Yen and Sun [19]designed an independent domination game and proved that every NE is a minimal independent dominating set.A distributed algorithm was also presented under a central daemon.Chen and Zhang [20] designed a connected domination game and proved that every NE is a minimal connected dominating set and a distributed algorithm can find an NE in linear rounds of interactions.An example was given showing that the game cannot guarantee Pareto optimality.All these game theoretical algorithms are sequential, i.e., players have to make decisions in turn.As far as we know, algorithms for the secure dominating set problem are rare, and existing algorithms are all used for special graphs.Our paper is the first one using game theory to compute a secure dominating set in general graphs.Furthermore, our algorithm allows players to make decisions simultaneously, only using local information.
Another closely related area of research is game theoretical algorithms for the minimum vertex cover (MinVC) problem[21]–[25].Different from the dominating set problem which uses vertices to monitor vertices, the vertex cover problem uses vertices to monitor edges.Nevertheless, many ideas used in these studies are very inspiring to our work.Yang and Li[21] used snowdrift games to study the MinVC problem, and devised a distributed algorithm, trying to find a vertex cover with a small size.Tanget al.[22] generalized the study to the weighted version, and designed an asymmetric game algorithm, trying to find a vertex cover with small weight.Sunet al.[23], [24] proposed a distributed algorithm for the Min-WVC problem based on relaxed greed and finite memory.They used potential game theory to prove its convergence to an NE.Chenet al.[25] proposed a weighted vertex cover game using a 2-hop adjustment scheme, trying to get a better solution.In all of these works, minimality of NEs were proved, but Pareto optimality was not discussed, which is a preferred quality of solutions from a social point of view.
In addition to the above works which are most closely related with our work, there are also many game theoretical studies on various coverage problems from different perspectives.For example, Liet al.[26], [27] employed cost sharing methods and mechanisms for a generalized set cover game.The focus was on whether players chose to lie.Fang and Kong[28] studied the core stability of vertex cover games.The core of a game is an important concept in cooperative game theory,which ensures that players have a willingness to participate.The cores of a domination game were studied by Velzen in[29], and the cores of a connected domination game were studied by Kim in [30].Another measure of the quality of a game theoretical solution is the price of anarchy (PoA), which is the ratio between the cost of a worst NE and the cost of a socially optimal solution.Aiet al.[31] studied PoA and computational complexity of a coverage game.Note that their algorithm is centralized.
In this paper, we study the MinSDS problem in a multiagent system using potential game theory.The main contributions are summarized as follows.
1)Game Design: We design a security domination game in multi-agent systems, in which every player determines himself to be a dominator or a dominatee.By carefully designing utility functions for the players, we show that every Nash equilibrium (NE) is a minimal secure dominating set (MSDS),as well as a Pareto-optimal solution.Furthermore, we prove that this game is an exact potential game, and thus NE exists.
2)Algorithm Design: Based on the above security domination game, we propose a best response dynamic distributed local algorithm (BRDDLA) for the secure dominating set(SDS) problem.The algorithm is distributed and local: in each round of the algorithm, every player decides by himself on his strategy based on local information in his 6-hop neighborhood.
3)Efficiency of Algorithm: We prove that BRDDLA can converge to an NE inO(n) rounds, wherenis the number of players.Hence the algorithm can find a minimal secure dominating set, which is also a Pareto-optimal solution, in linear time.Since the MinSDS problem is NP-hard, so minimal solutions and Pareto-optimal solutions that can be obtained in linear time are fairly good.Furthermore, an NE solution achieves a kind of balance in a multi-agent system, which is also a desirable property.
4)Verification of Performance via Simulation: Simulations are done to experiment on the performance of our algorithm on randomly generated graphs.Since there is no previous algorithm on MinSDS in general graphs (GA), we compare BRDDLA with a natural greedy algorithm.It turns out that BRDDLA can obtain a much better solution than GA.Furthermore, we compare the algorithm with the exact algorithm on trees.It turns out that the output of BRDDLA is close to optimal solutions.Furthermore, the number of rounds of BRDDLA is less than those of reference algorithms, especially on the random tree graphs.It is also interesting to note that when testing the effect of decision priority on the performance of the algorithm in a Barabasi-Albert (BA) graph, a better performance can be reached if we let players decide in the order that the vertices are generated by the BA model.This might suggest that the earlier a vertex is generated in a BA graph, the more important it might be.
The remaining parts of the paper are organized as follows.Section II introduces preliminaries in game theory which are used in this paper.Section III designs the security domination game.Section IV provides strict theoretical analysis for the game.Section V describes the algorithm in details and provides theoretical analysis on its convergence.Section VI evaluates the performance and complexity of the algorithm through extensive simulation.Section VII concludes the paper with some discussions on future work.
II.PRELIMINARIES
In this section, we give the formal definition of SDS, and some basic terminologies and notations of graph theory and game theory.Main notations are summarized in Table I.
LetG=(V,E) be a graph with vertex setVand edge setE.We say that two verticesviandvjare adjacent if (vi,vj)∈E,in this case, we also say thatviandvjare neighbors of each

TABLE I LIST OF NOTATIONS


III.SECURITY DOMINATION GAME

Assume that all players are selfish, intelligent and rational,in the sense that they will not consider the benefit of the other players while seeking to maximize their own benefits.The most critical part of the game is to design good utility functions for the players such that a stable and reasonable social status can be reached through cooperation and competition among players.The following are some preferred features of a game.
1)Self-Stability: Starting from any initial state, the game can end up in an NE which corresponds to a secure dominating set.
2)Small Size: The cardinality of the SDS corresponding to an NE should be reasonably small.Since the computation of a minimum SDS is NP-hard even using centralized algorithms,we cannot hope for a minimum SDS in reasonable time.An alternative requirement is that the computed SDS should be minimal, that is, removing any vertex will no longer be an SDS.
3)Time Efficiency: The time for the game to reach an NE should be polynomial in the size of the instance.
We define utility functions as follows.For a strategy profileC=(c1,c2,...,cn), the utility function ofviis defined as
wheregi(C) andqi(C) are defined to be
wheremk,j(C) is an indicator function defined as

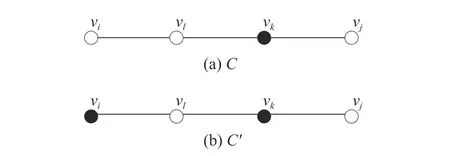
Fig.1.An example illustrating Property 2.
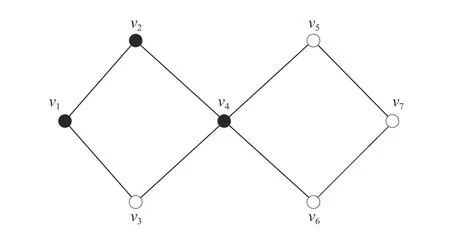
Fig.2.An example illustrating the ideas behind the definition of utility function ui.Blackened vertices are selected vertices in strategy profile C.

IV.THEORETICAL ANALYSIS
In this section, we analyze the theoretical properties of the security domination game designed in the above section.In the following, we shall useCto denote both a strategy profile(c1,...,cn)∈Σ and the vertex set {vi:ci=1} it corresponds to.We assume that a player is willing to change his strategy only when he can bestrictlybetter off.
A. Nash Equilibrium Solution
In this subsection, we show that an NE of the game always corresponds to a minimal secure dominating set.The proof makes use of the following property and Lemma 1.
Property 3:Foranyplayervi∈VandtwoprofilesC?C′,we havemk,j(C)≥mk,j(C′)foranyvj∈Vandvk∈Dj(C).

B. Potential Game and Existence of NE
Note that a game in strategic form does not necessarily have a pure Nash equilibrium [32].However, a potential game always has a pure Nash equilibrium [33].In this subsection,we prove the existence of NE for our game by showing that it is a potential game, and show that an NE can be reached in linear rounds of interactions among the players.
Definition 8(Exact Potential Game): We call a game

Lemma 2: The proposed security domination game is an exact potential game.
Proof: We prove that the following function is a potential function:
Denote the two terms ofπ(C) as π(1)(C) and π(2)(C), respectively.
LetC=(ci,C-i) andC′=(,C-i) be two strategy profiles beforeandafter somevichangesitsstrategyfromcito.We mayassume, without loss ofgenerality,thatci=0and=1.It can be calculated that
and
where the second equality holds because of Property 2 and thus the second and the fourth terms are cancelled.Combining (5) and (6), we have
Theorem 2: The secure domination game always has an NE.Furthermore, starting from any initial state, the number of iterations needed for the security domination game to reach an NE is at most


C. Pareto Optimality
Note that an NE is a stable state from the view of individual players, in which no single player can be strictly benefited by unilateral deviation.While a Pareto optimal solution is a stable state in which a strict benefit for some players will definitely harm the interest of some others, which is from the view of social welfare.This subsection shows that any NE of the game is also Pareto optimal.
Theorem 3: Every NE of the security domination game is a Pareto-optimal solution.

D. Relation of the Solutions

V.ALGORITHM DESIGN AND ANALYSIS
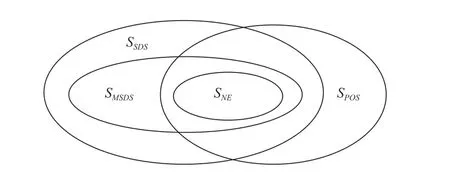
Fig.3.Relations between solution sets S S DS, S MS DS, S NE and S POS.
To realize the above SDS game, one may let players make their decisions in order until no player can improve his utility.Theorem 2 guarantees that in this way, the algorithm converges to an NE inO(n) rounds.However, this algorithm is not distributed and is quite time consuming (since every player has to wait for the decisions of the other players).

The reason why a mess might be created by a simultaneous decision is as follow: A best response of a player is based on the assumption that all the other players keep their strategies;thus, if two correlated players change their strategies simultaneously, then their best responses for the previous strategy profile are no longer best responses for the strategy profile after the simultaneous change.
An idea to avoid such a mess is to let only a set of independent players make decisions simultaneously.By the definition of utility functionui(C), it is easy to see that playervican make his decision on local information which is at most six hops away fromvi.The following argument shows that a little more storage space may further reduce the dependence on local information to at most three hops.

The distributed algorithm is described in Algorithm 1.To emphasize the range of information needed for a computation,we use a subscript.For example,BR(vi,CNi3) indicates that only information inNi3is needed forvito compute a best response.The details for the execution of the algorithm are explained as follows.Algorithm 1 is a distributed realization of the SDS game presented in Section II, where parameterthe reason of which will be clear after proving Lemma 4.For current strategy profileC, we denote the marginal utility of playervibymui(C)=ui(BR(vi,CNi3),C-i)-ui(ci,C-i).All players compute their marginal utility simultaneously, but not all of them change their strategy at the same time.A playervidecides to change his strategy only when

Algorithm 1 Best Response Dynamic Distributed Local Algorithm (BRDDLA)Input: An initial strategy profile C′Output: A minimal SDS C ←C(0)1:C(0)=(c(0)1 ,...,c(0)n )2: for do t=1,2,...,T 3: for every player (this is done simultaneously) do c′i ←BR(vi,CN3i ) S S j vj ∈N3i 4: by accessing for mui ←ui(c′i,C-i)-ui(ci,C-i)5:vi 6: if satisfies (7) then ci ←c′i 7:8: end if 9: end for vi C=C(t-1)10: if then 11: Break and go to line 12: else C(t)←C 13:14: end if 15: end for C′←C 16: Output 16
That is, the playervihas the priority to change his strategy only when he has the smallest ID among players inwith a strictly positive marginal utility.
The reason why we use (7) to determine who can change strategy is based on the following property.
Property 4: Suppose H is the set of players who have changed their strategies simultaneously in one execution of the inner for loop of Algorithm 1; then H is a 3-hop independent set in the SDS game, that is,
As a consequence, if a strategy profile C changes intoC′,then for any playerviwho has changed his strategy by rule(7), his best response to C is also a best response toC′.
Intuitively, since decisions are made locally, only allowing players who are somewhat distant to change strategies can effectively decouple mutual influences, and thus leads to a guaranteed convergence rate.We give a strict analysis for this intuition in the following.
Lemma 3: Suppose C is the current strategy profile.After a round of the inner for loop of Algorithm 1, the new strategy profile is), where H is the set of players who have their strategies changed in this round.Then,

The following theorem shows the quality of the solution.
Theorem 4: The outputC′of algorithm BRDDLA is a minimal secure dominating set and a Pareto-optimal solution.
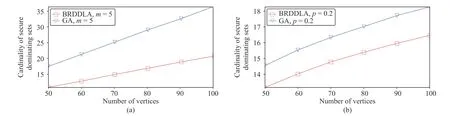
Fig.4.Comparison between BRDDLA and GA.(a) BA, m 0=5; (b) ER, p=0.2.
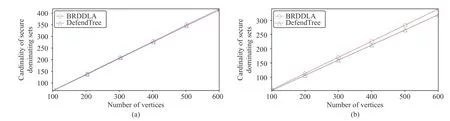
Fig.5.Comparison of BRDDLA and DefendTree on trees.(a) BAT; (b) RT.
Proof: We claim that whenC=C(t-1),Cmust be an NE.In fact,Cstops being updated only when no player can be strictly better off.Thus, the reason whyC=C(t-1)is becauseC(t-1)consists of best responses for every player, and thus is an NE.Then, the theorem follows from Theorems 1 and 3.■
VI.SIMULATION RESULTS
In this section, we experiment on the performance of our algorithm BRDDLA.All experiments are coded in Python and run with an identical configuration: AMD Ryzen 5 3500U with Radeon Vega Mobile Gfx and 16 GB of RAM.
A. Comparison With a Greedy Algorithm
Although there are some polynomial-time algorithms for MinSDS on special classes of graphs [4], [8]–[15], we have not found any algorithm on MinSDS designed for a general graph.Hence, we compare our algorithm with a natural greedy algorithm (GA) described in Algorithm 2, whereIS(C)denotes the set of insecure vertices inVwith respect to current solutionC.The algorithm iteratively selects a vertex the addition of which reduces the number of insecure vertices most.By Lemma 1, the whole vertex setVis an SDS, and thus GA terminates in at mostnrounds.

Algorithm 2 Greedy Algorithm (GA)Input: graph G Output: an SDS C IS(C)≠?1: while do vi ←argmaxvi∈VC{|IS(C)|-|IS(C ∪{vi})|}2:3:4: end while C ←C ∪{vi}
Graphs for the experiments are generated randomly using the following two models.
1)The Barabási-Albert Graph(BA)[34]: Starting from a graph with a small numberm0of vertices, new vertices are iteratively added.When a new vertex is added, it is connected tomexisting vertices, wherem≤m0, and the probability that an existing vertex is linked with the new vertex depends on its current degree.
2)The Erdo¨s-Rényi Graph(ER)[35]: In this graph, every edge is presented with probabilitypindependent of the other edges.
In Fig.4, the horizontal axis is the number of verticesn.For eachn, 1000 sampled graphs are generated.The vertical axis is the average size of computed solutions.It turns out that BRDDLA is superior to GA, especially in BA, where the average sizes of the solutions computed by BRDDLA are roughly 59% of those computed by GA.For clarity of figures,we only show the case whenm=m0=5 for the BA, andp=0.2 for the ER.In fact, when we tested on otherm,m0andp, all experiments support the same results.
B. Comparison With an Exact Solution on Trees
To see the accuracy of our algorithm, we compare BRDDLA with the exact algorithm DefendTree proposed by Burgeret al.[4] for MinSDS on trees.Trees for the experiments are constructed in the following two manners.
1)Barabási-Albert Tree(BAT): A tree is constructed by the Barabási-Albert model withm0=2 andm=1.
2)Random Tree(RT): LetVbe a vertex set onnvertices andFbe the edge set consisting all possible edges between vertices ofV.Starting from an empty graph on vertex setV,iteratively add an edgeefromFrandomly and uniformly as long as no cycle is created, until we obtain a spanning tree onV.
Again, for eachn, 1000 trees of sizenare sampled.Fig.5 shows the average sizes of solutions computed by BRDDLA(red line) and the average sizes of optimal solutions computed by DefendTree (blue line).It can be seen that these two lines are very close.We useto measure relative error of BRDDLA, whereC′is the output of BRDDLA andC?is the optimal solution computed by DefendTree.It can be seen from Table II thatγis around 1% for BAT and 6% for RT.

TABLE II RELATIVE ERROR OF BRDDLA MEASURED BY γ
C. Effect of Decision Priority
Theoretical analysis guarantees that BRDDLA could always find a minimal SDS, but different minimal solutions may have different sizes.According to decision rule 7, a player with a smaller ID has a higher priority to make a change.So, a question is: will different ID of players lead to solutions with much difference?

Tables III and IV show the values ofωandηin various types of experimental graphs.
From Table III, it can be seen that for a general graph, there is a big difference between the best solution and worst solution, and the difference is relatively smaller for ER than for BA.This indicates that sizes of different minimal solutions might vary greatly, and the variance is smaller in an evenly distributed graph than in a power-law graph.While for trees,the difference is much smaller, and smaller for BA than for ER.This might be because our algorithm is already fairly accurate for trees, especially for power law graphs.These experiments certify that different IDs of players do make a difference in the quality of the solution obtained by BRDDLA, which also suggests that in order to obtain a better solution, one may repeat the algorithm several times based on different ID arrangements.
What is most interesting is to observe from Table IV that the improvement brought about by decision priority is significantly smaller for BA than for ER.The reason might be explained as follows.For BA, (1,2,...,n) is the order of vertices added in the construction of the graph.A vertex which is added earlier has a larger chance to be an important individual, and thus letting such the vertex to make a decision earlier may have a better chance to create a good result.While in ER,importance of vertices is distributed evenly, and thus trying different players’ IDs might result in more diversified solutions.In summary, changing players’ ID might improve the performance of the algorithm for evenly distributed random graphs, while for BA, letting players’ IDs be equivalent to construction order might be good enough.
D. Effect of Initial Solution
In the above experiments, the initial strategy profile is always taken to beC(0)=(0,...,0).Although Lemma 2 guarantees that BRDDLA could converge to an NE starting from any initial strategy profile, we would like to know the influence of initial strategy profile on the final output.For this purpose, we use a simple method: restart.
The results are shown in Fig.6.For each type of graphs, 10 sample-graphs are generated.For each graph, 100 initial strategy profiles are taken uniformly and randomly, and the smallest size of these 100 solutions is recorded as the “result of restart”.In Fig.6, the green lines mark the results of restart,and the red lines mark the sizes of those solutions starting from strategy profile (0,...,0).It turns out that the effect of restart is obvious on ER and RT, but not so obvious on BA and BAT.The reason might be similar as before: our algorithm is already good enough for the BA model, which leaves only a little space for improvement.
E. Convergence Rate
In this subsection, we test on the number of rounds needed by DefendTree, GA and BRDDLA on BA, ER, BAT and RT.The number of vertices is 1000.The results are shown in Table V.As Lemma 4 shows, BRDDLA converges inO(n)rounds, wherenis the number of vertices.This is a theoretical result.It turns out that in a practical setting, BRDDLA converges in much less rounds thann.Furthermore, BRDDLA converges faster than the reference algorithms, especially on BAT and RT.The reason might be that both BAT and RT are sparse, and thus more players can change their strategies simultaneously.
VII.CONCLUSION
In this paper, we use the game theoretic method to solve the MinSDS problem in a multi-agent system.An SDS game was proposed and proven to be an exact potential game, converging to an NE in linear rounds of interactions.Moreover, we proved that every NE of the game is a minimal secure dominating set and a Pareto optimal solution.Then, a distributed algorithm was designed to simulate the game process.In each round of the algorithm, every player only uses local information at most three hops away to make his decision.The performance of our algorithm was tested through experiments on randomly generated graphs using both ER and BA.We compare its performance with a natural greedy heuristic, and it turns out that our algorithm out-performs the greedy strategy by a large amount.Compared with an existing exact algorithm for MinSDS on trees, our algorithm turns out to be fairly accurate.Furthermore, our algorithm is not only better in accuracy, but also faster in convergence.
There might be a lot of interesting topics to be further explored, such as price of anarchy (PoA) [36], allocation games [37], evolutionary games [38] and networked games[39], [40].

TABLE III INFLUENCE OF DECISION PRIORITY MEASURED BY ω

TABLE IV IMPROVEMENT BY DECISION PRIORITY MEASURED BY η
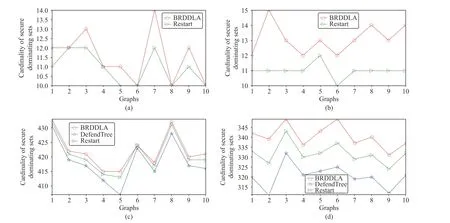
Fig.6.Effect of Initial Solution by Restart.(a) BA, m 0=m=5, | V|=50 ; (b) ER, p=0.2, | V|=50 ; (c) BAT, | V|=600 ; (d) RT, | V|=600.

TABLE V NUMBER OF ROUNDS OF THREE ALGORITHMS
 IEEE/CAA Journal of Automatica Sinica2023年12期
IEEE/CAA Journal of Automatica Sinica2023年12期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Knowledge Transfer Learning via Dual Density Sampling for Resource-Limited Domain Adaptation
- Subspace Identification for Closed-Loop Systems With Unknown Deterministic Disturbances
- Magnetic Field-Based Reward Shaping for Goal-Conditioned Reinforcement Learning
- Multi-Blockchain Based Data Trading Markets With Novel Pricing Mechanisms
- GenAI4Sustainability: GPT and Its Potentials For Achieving UN’s Sustainable Development Goals
- Resilient Event-Triggered Control of Connected Automated Vehicles Under Cyber Attacks
