Complete population transfer between next-adjacent energy levels of a transmon qudit
Yingshan Zhang(張穎珊), Pei Liu(劉培), Jingning Zhang(張靜寧), Ruixia Wang(王睿俠),Weiyang Liu(劉偉洋), Jiaxiu Han(韓佳秀),?, Yirong Jin(金貽榮), and Haifeng Yu(于海峰)
1Beijing Academy of Quantum Information Sciences,Beijing 100193,China
2State Key Laboratory of Low Dimensional Quantum Physics,Department of Physics,Tsinghua University,Beijing 100084,China
Keywords: transmon qudit,complete population transfer,Pythagorean coupling
1.Introduction
Qudits (quantum computational units withdenergy levels)have been a significant resource for quantum information and computation.[1-4]Benefiting from the extra energy levels and the larger Hilbert space,the utilization of qudits instead of qubits can enhance the efficiency of quantum gates,[5]increase noise tolerance,[6,7]and improve channel capacity.[8]A crucial technical requirement for practical applications of qudits is the controllable population transfer between energy levels.Especially,complete population transfer between non-adjacent energy levels provides a pivotal mechanism for preparing and manipulating quantum states,making it an indispensable tool in a wide range of qudit-based applications,such as quantum error correction[9]and remote entanglement.[10]
Realizing population transfer between adjacent energy levels in a qudit is relatively straightforward, but it becomes more challenging when attempting to transfer between nextadjacent levels.Several methods have been developed to perform such a transfer, including pulse trains consisting of multiple adjacent-transfer operations, stimulated Raman adiabatic passage(STIRAP)[11,12]and optimal control.[13]However, these approaches suffer from either long operation time or complicated optimization procedures.The Pythagorean coupling approach[14]may be an under-explored solution that provides a convenient avenue for rapid exchange of quantum information between next-adjacent energy levels without the need for special pulses or optimization.This approach has been demonstrated on a superconducting phase qudit,[15]but the very finite anharmonicity of the phase qudit led to a transition from SO(4) to SU(4), which significantly limited the transfer speed,and the transfer fidelity was also adversely affected by the short qudit lifetime.
The transmon[16,17]is a promising qudit platform[18-20]due to its long coherence time,[21,22]adequate anharmonicity for gates as short as tens of nanoseconds with little leakage, and its compatibility with multi-level readout.[18,23]In this work, we reposition the Pythagorean coupling as a valuable method for qudit operations by combining it with a more appropriate type of qudits.Using the method of Pythagorean coupling and energy level mapping,we experimentally investigate the population transfer process between next-adjacent energy levels in our transmon qudits.We also explore the timescale for fast and leakage-free complete population transfer allowed by the anharmonicity of our transmon qudit, and we find it comparable to the transfer operation between adjacent energy levels,as short as 20 ns.
2.Theoretical model
Consider a 4-dimensional cyclic nearest-neighborcoupled system, where|0〉,|1〉,|2〉, and|3〉 represent the eigenstates of the four energy levels.The Hamiltonian of the system is represented as
whereVij(∈R) describes the coupling strength between theith andjth energy levels.According to the work by Suchowskiet al.,[14]a complete population transfer between|0〉 and|2〉occurs when the values ofVi jsatisfy the relation

which is mainly determined byΓ a.
Sincekis the extra degree of freedom for the dynamics,we can set one of theVi jterms equal to zero by choosing the value ofk,for example,
(1)k=0, so thatV01=Γ c,V12=Γ a,V23=Γ b, andV03=0;
(2)k=-a/b, so thatV01=Γ b,V12=0,V23=Γ c, andV03=-Γ a;
(3)k=b/a, so thatV01=Γ a,V12=Γ c,V23=0, andV03=Γ b.
We reduce the four coupling coefficients to three by selecting proper values ofk, which brings convenience to the implementation of the Hamiltonian.
3.Results
We demonstrate the process of population transfer between next-adjacent energy levels on superconducting transmon qudits, where the first four energy levels are taken into consideration.Our experiments involve two qudits,denoted asQ1andQ2,with their basic parameters listed in Appendix A.The reasonable anharmonicity ensures fast population transfer while avoiding leakage, and largeT1protects the population from decay.Moreover,the population of the four energy levels can be obtained simultaneously from a single-shot readout.We realize the couplingsVijby applying a multi-tone microwave pulse ∑Vijcos(ωijt) to the qudit.The frequency of each tone is determined byωij=ωj-ωi,whereωirepresents the eigen-frequency of|i〉,and the amplitude of each toneVijis calibrated individually through a Rabi experiment between the energy levels|i〉and|j〉,with the corresponding oscillation frequency?ij/(2π)=Vij.
We investigate the complete population transfer between|0〉 and|2〉 onQ1withk=0, so the couplings satisfyV01:V12:V23=c:a:b, as shown in Fig.1(i).We initialize the system to the state(1,0,0,0)T,where the population of|0〉is unity and|1〉,|2〉,and|3〉are all unoccupied.WithV12=Γ abeing constant at 1.5 MHz, we vary the strengths ofV01andV23,and then measure the population of each energy level after a timeTCT(p=3,q=1),noting thatTCT(p>3,q=1)≈TCT(p=3,q=1).Figure 1 illustrates that a complete population transfer between|0〉 and|2〉 occurs when the values ofVijsatisfy the Pythagorean coupling relation.We observe three PPTs corresponding to (p,q) = (3,1), (p,q) = (5,1),and(p,q)=(7,1),as denoted by+markers for the simulated results in Figs.1(c) and 1(g), and x markers for the experimental results in Fig.1(g).The experimental transfer matches well with the simulated results for smallVij, but a slight deviation appears at largeVij.This discrepancy arises from the strongly nonlinear behavior of the IQ mixer under the highpower multi-tone microwave pulse, which makes the actualVijdiffer from the expected intensity.Our results show a maximum|2〉 population of 90.72% (Fig.1(i)).We note that the readout error is uncompensated in these measurements, and the actual transfer population is higher (see more details in Appendix A).
In the previous study[15]on phase qudit,due to weak anharmonicity, a strong microwave pulse caused the dynamics of the qudit to transit from SO(4)to the full SU(4)dynamical space,thereby preventing population transfer asVijincreased.Here,we attempt to investigate the critical driving strength for our transmon qudit by increasingVi jwhile maintaining a ratio of(a,b,c)=(3,4,5).Regrettably,the poor coupling ofQ1with its driving channel forces us to proceed with the experiment usingQ2, despite its unstable energy levels and readout fidelities.As indicated by the experimental results, over the entire range of available drive strengths, the evolution of each energy level corresponds well with the simulated SO(4)dynamics based on the Hamiltonian (1), thus confirming that no transition to SU(4) occurs (Fig.2).This implies the anharmonicity of our qudit facilitates fast next-adjacent energy level operations.We successfully achieve a complete population transfer between|0〉and|2〉in 20 ns,which is a timescale comparable to adjacent energy level transfers, as shown by a red dot in Fig.2(f).The variation in brightness of the experimental data in Fig.2 is caused by the instability of the readout fidelity.In the simulation,the nonlinear pulse intensity and the effects of rising and falling edges of the pulses are taken into consideration(further details are available in Appendix C).
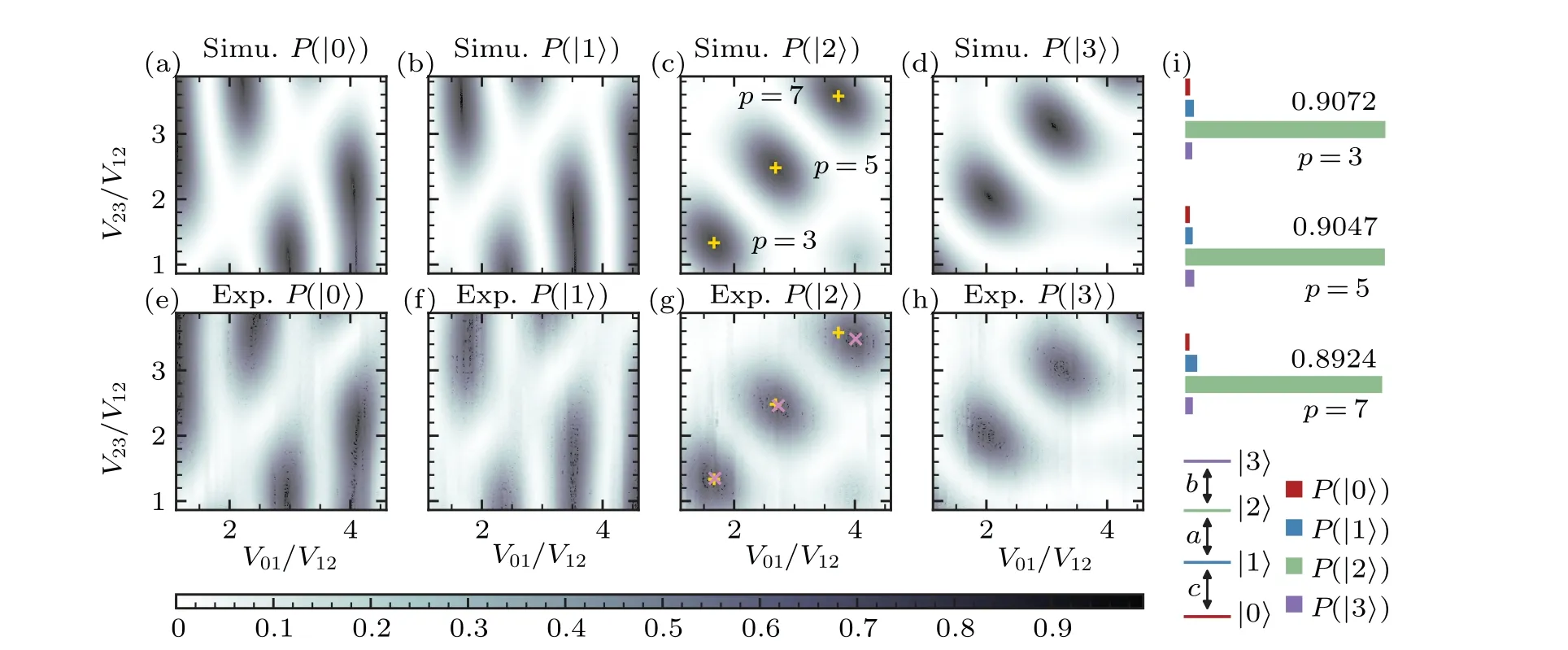
Fig.1.The population of four energy levels while maintaining V12 and TCT, and sweeping the strengths of V01 and V23.Panels (a)-(d)represent the simulated ideal results without considering any noise.Panels (e)-(h) show the experimental data.Gold + markers denote the theoretical PPTs of(p,q)=(3,1),(p,q)=(5,1),and(p,q)=(7,1)where complete population transfer occurs.The violet x markers indicate the experimental complete transfer conditions.Panel (i) illustrates the population of |2〉 after the transfer process for the three PPTs with uncompensated readout error.

Fig.2.The population of four energy levels with respect to V12.We proportionally increase the values of Vij while keeping the ratio of V01 :V12 :V23 =5:3:4.Panels (a), (c), (e), and (g) present the numerical simulation results of the evolution.Panels(b),(d),(f),and(h)show the corresponding experimental data.The red dot in (f) shows a transfer operation as fast as 20 ns.
We conduct further investigations on the transfer process.The propagator for the complete population transfer between|0〉and|2〉is determined by the PPT as
We utilize quantum process tomography(QPT)to benchmark the fidelity of the transfer operation.The quantum process is represented by
where ?λkrepresents the identity matrix ord2-1 generators of SU(4)group.The process fidelity is calculated by
and one can find more details in our previous work.[23]Figure 3 shows the experimental and theoreticalχmatrix of the process, with a process fidelity of 71.05%.The dominant error arises from the poor readout fidelity and stability of|3〉, which results in inaccuracies in the matrix elementsχk,l(k,l ∈[9,15]).To mitigate the impact of this error, we restrict our analysis to the subspace spanned by the first three energy levels|0〉,|1〉, and|2〉, and define the process in this subspace by truncating theχmatrix to its first 9×9 elements.The fidelity of the transfer process in this subspace is 97.76%.In addition to the state preparation and measurement(SPAM) errors, experimental imperfections, such as nonlinearity in the multi-tone microwave pulse,signal distortion and the frequency splitting caused by charge noise,also introduce operational errors during the transfer process.Furthermore,decoherence further decreases the fidelity of the process.
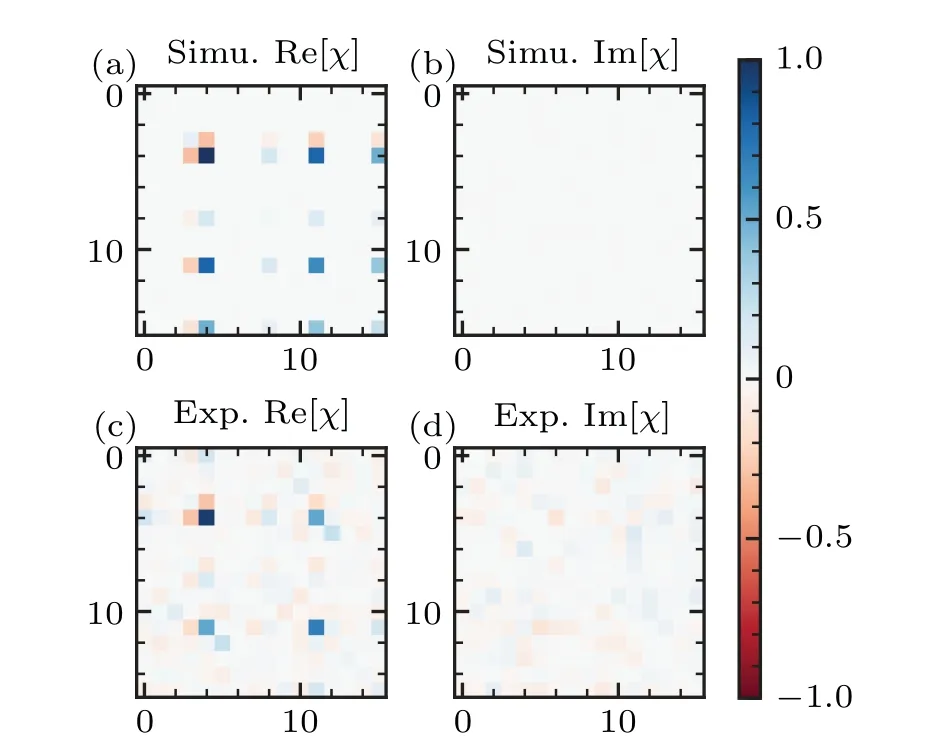
Fig.3.The χ matrix for the process of complete population transfer between |0〉 and |2〉 with (a,b,c)=(3,4,5).Panels (a) and (b) show the ideal χ matrix obtained via numerical simulation.Panels(c)and(d)show the experimental χ matrix.
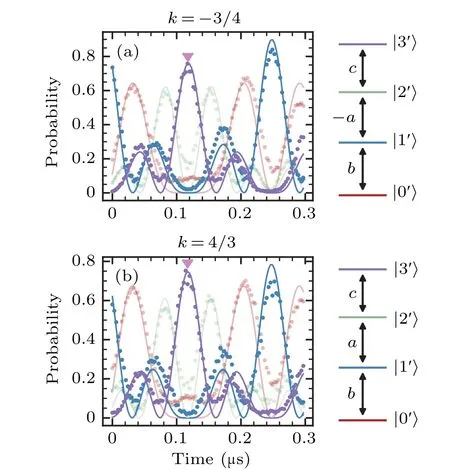
Fig.4.The population evolution for four energy levels of a qudit as a function of microwave pulse duration.The colors represent the qudit’s energy levels.The experimental data is shown as dots, while the simulated results, which consider SPAM error, nonlinear drive, and pulse shape, are displayed as lines.The violet inverted triangles illustrate the population transfer from |1〉 to |3〉.Panel (a) corresponds to the case of k=-a/b and (a,b,c)=(3,4,5), with the mapping given by|i′〉=|(5-i)mod 4〉.Panel(b)corresponds to the case of k=b/a and(a,b,c)=(3,4,5),with the mapping given by|i′〉=|(i+1)mod 4〉.
Finally,we demonstrate the complete population transfer between|1〉and|3〉using a method of energy level mapping.For example,for the case ofk=-a/b,we apply the mapping|i′〉=|(5-i)mod 4〉to the energy levels,where|i〉represents the energy levels in the HamiltonianH,and|i′〉represents the energy levels of the transmon qudit.With the mapping, the Hamiltonian parametersV01:V23:V03=b:c:-aandV12=0 are mapped toV0′1′:V1′2′:V2′3′=b:-a:candV0′3′=0.So,the transfer between|0〉and|2〉of the Hamiltonian is mapped to a transfer between|1′〉 and|3′〉 of the transmon qudit.As shown in Fig.4,the population transfer between|1′〉and|3′〉is observed experimentally for both cases ofk=-a/bandk=b/awith their corresponding mappings.The experimental results agree well with the simulation,where SPAM error,drive non-linearity and pulse shape are taken into account.
4.Conclusion
In this study,we achieve complete population transfer between|0〉and|2〉as well as between|1〉and|3〉in a transmon qudit using Pythagorean coupling and energy level mapping.Our experimental results demonstrate high-fidelity population transfer with a timescale comparable to the transfer between adjacent energy levels without any leakage out of SO(4) dynamics.
Our results have important implications for manipulating qudit states and can play an important role in a wide range of scenarios.For instance, the transfer operation provides a way to realize modular quantum computation by protecting one level from the environment while coupling another level strongly to the environment, where the two levels serve as a computing node and a microwave interface,respectively.This precise and efficient operation in qudits opens doors for the qudit-based quantum computation, communication, simulation,and cryptography.We hope that our findings will inspire further research on qudits and contribute to unlocking the potential of qudit-based quantum information processing.
Appendix A: Characteristic parameters of the transmon qudits
The experiments in the main text involve two transmon qudits,denoted asQ1andQ2.We characterize their basic parameters, and list them in Table A1.The ratio ofEjandEcforQ2is smaller thanQ1, which results in the instability of resonant frequencies for the higher energy levels.We can observe a beating pattern in Ramsey fringe experimentally for the higher energy levels ofQ2, which affects the accuracy of drives,and further affects the readout fidelity and stability for the higher energy levels.AlthoughQ1has more stable performance,its weak coupling to the drive line limits the gate speed and forces us to turn toQ2to demonstrate fast transfer.
We also characterize the state preparation and measurement (SPAM) features of the two qudits, as summarized in Table A2.We can mitigate this error by employing a Bayesian correction using the matrix presented in Table A2.Consequently, in Fig.1 of the main text, we state that the actual population of|2〉 after the transfer process exceeds 90.72%.We note that the preparation and readout fidelity ofQ2is much lower compared to that ofQ1,thus necessitates Bayesian correction during the QPT investigation.

Table A1.Basic parameters of the two transmon qudits.
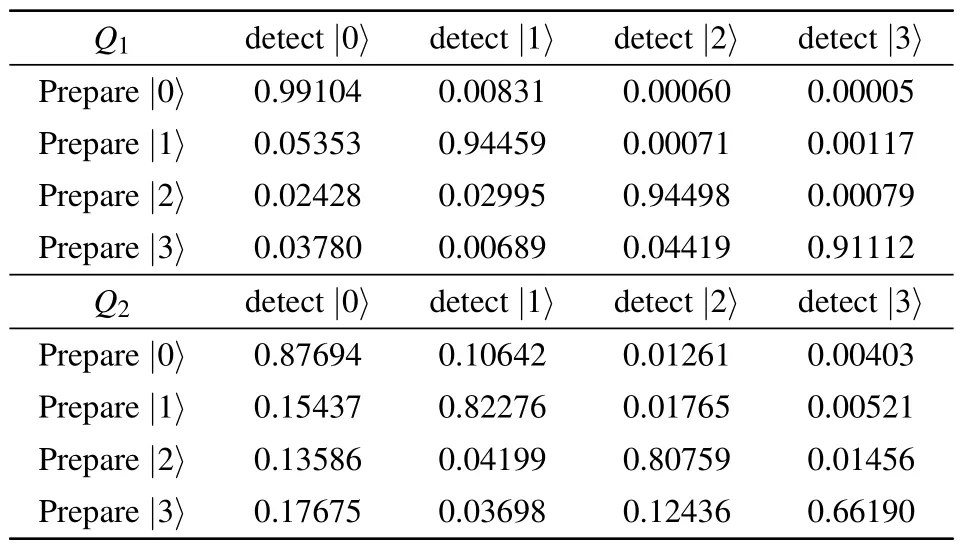
Table A2.Preparation and readout fidelity.
Appendix B:Non-linearity of the drives
In our experiments,the microwave pulses are modulated by an IQ mixer.However, we observe that the IQ mixer suffers from nonlinear effects when the signal strength is high.For instance, during the calibration ofV23forQ1, the corresponding Rabi oscillation frequencies exhibit a clear nonlinear relationship with the drive amplitude,as shown in Fig.B1.We incorporate this effect into our numerical simulation.

Fig.B1.An example for the non-linearity of microwave drives.
Appendix C:Numerical simulation of the evolutions
We develop a simulation model considering several experimental imperfections.Firstly, the microwave pulses employed in our experiments possess a linear rising and falling edge of 10 ns.As a result,we adjust our simulation to mimic these experimental conditions.Secondly, we observe that the nonlinear effect becomes more pronounced when applying a multi-tone pulse compared to calibrating the single-tone pulses individually.Consequently,we incorporate a nonlinear correction parameter for each drive into our simulation model,which is multiplied by the drive strength.This adjustment allows us to appropriately account for the nonlinear effect.Finally,to facilitate a more accurate comparison between the experimental and simulation results,we introduce a set of coefficients,and multiply a coefficient by the numerical probability for each energy level.These coefficients serve to simulate SPAM errors, enhancing the overall correspondence between the experimental and simulated outcomes.
In the main text,the simulated results shown in Fig.1 are from an ideal model without any modifications.While for the simulation shown in Fig.2,we consider the rising and falling edges of the pulses and driving non-linearity.Since the preparation and readout fidelity is unstable forQ2during the period we take the data,we cannot compensate this error with a fixed matrix,so this error is remained uncorrected.And for the experiment shown in Fig.4,we do all the above modifications in our simulation.
Acknowledgements
Project supported by the National Natural Science Foundation of China(Grant Nos.11890704,12004042,12104055,and 12104056),Natural Science Foundation of Beijing(Grant No.Z190012),and Key Area Research and Development Program of Guangdong Province(Grant No.2018B030326001).
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Multi-channel generation of vortex beams with controllable polarization states and orbital angular momentum
- Calibration of quantitative rescattering model for simulating vortex high-order harmonic generation driven by Laguerre-Gaussian beam with nonzero orbital angular momentum
- Materials and device engineering to achieve high-performance quantum dots light emitting diodes for display applications
- From breather solutions to lump solutions:A construction method for the Zakharov equation
- Ultralow-temperature heat transport study of noncentrosymmetric superconductor CaPtAs

