Asymmetric scattering behaviors of spin wave dependent on magnetic vortex chirality
Xue-Feng Zhang(張雪楓), Je-Ho Shim(沈帝虎), Xiao-Ping Ma(馬曉萍),Cheng Song(宋成), Haiming Yu(于海明), and Hong-Guang Piao(樸紅光)
1Hubei Engineering Research Center of Weak Magnetic-Field Detection,China Three Gorges University,Yichang 443002,China
2Department of Physics,College of Science,Yanbian University,Yanji 133002,China
3Key Laboratory of Advanced Materials(MOE),School of Materials Science and Engineering,Tsinghua University,Beijing 100084,China
4Fert Beijing Institute,School of Integrated Circuit Science and Engineering,Beijing Advanced Innovation Center for Big Data and Brain Computing,Beihang University,Beijing 100191,China
Keywords: magnonics,magnetic vortex,spin wave,magnetic chirality
Nonlinear science is an interdisciplinary science which studies the common law of nonlinear behaviors in various systems.[1,2]In recent years, nonlinear interaction between spin wave (magnon) and topological magnetic texture (magnetic soliton)has received a great deal of attention in magnetic systems,[3,4]because it provides a good platform for exploring nonlinear science and has potential application prospects.[5-7]In many nonlinear magnetic systems,the equilibrium position(vortex core position in the steady state)of magnetic vortices exhibits notable robustness.[8]In other words,the vortex structure remains remarkably stable even under the interference of the external field.Hence, the interaction between spin waves(SWs) and magnetic vortices can provide a stable platform for research of nonlinear dynamics and may have application prospects in the field of spintronics.[9]
SWs,as a collective precession behavior of spins in magnetic systems,[10,11]can transmit information using spin angular momentum rather than electron as a carrier, which can effectively solve the problem of thermal effect related power consumption caused by electron scattering.Since SWs has a wide frequency range from GHz to THz and their wavelengths can also reach nanometer scales,[12,13]it is advantageous to transmit information in magnetic nanodevices.Particularly,since they can propagate in magnetic materials, wave properties like diffraction,[14]refraction,[15]and interference[16,17]can be used to realize a variety of useful functions.At present,some SW-based functional devices have been reported, such as SW-based diodes and logic devices.[18-20]Interestingly, a nonreciprocal behavior of SW propagation can be achieved by modulating Dzyaloshinskii-Moriya interaction[21,22]and magnetic anisotropy[23,24]in magnetic systems, which is expected to be applied to the magnonic logics as an asymmetric behavior.However, it is obvious that the best way to apply magnonics is not to control the SW behaviors by changing the inherent structural properties of magnetic materials.Therefore, it will be of great significance for development of ultrafast, low power consumption and stable performance magnonic devices if the control of SW behavior can be realized through reconstruction of magnetic texture.[25]
Recently, it has been found that behaviors of SW propagation become richer and easier to be controlled with introduction of topological spin textures,[4]due to the fact that the spin texture exhibits structurally stable soliton-like dynamic behavior,[26,27]which can produce SWs when excited by an external field and influence the behavior of SWs as they propagate.[27-29]Among various spin textures, the magnetic vortex not only effectively excites SWs[30,31]through the gyromotion,[32,33]azimuth mode motion[34,35]or radial mode motion[36]of its core, but also controls the SW propagation behaviors by switching its chirality.[30]The vortex has two chirality with right and left handedness,[37]which are characterized by the circulation sense of the in-plane circling spins[c=-1 for clockwise(CW),c=1 for counterclockwise(CCW)]and the polarity of the vortex core(VC)(p=1 for upward core,p=-1 for downward core).That is,there are four chiral states:vortex(1,1)and vortex(-1,-1)for right-handed chirality,and vortex(1,-1)and vortex(-1,1)for left-handed chirality.Therefore, if the propagation behavior of SWs can be effectively manipulated by controlling the four chiral states of the magnetic vortex,it will benefit the design of magnonic devices and promote the exploration of nonlinear science.
In this paper,an asymmetric SW scattering behavior,depending on the chirality of magnetic vortices, is investigated in a cross-shaped ferromagnetic nanostructure.The results show that there are four scattering mechanisms in the magnetic system,including asymmetric skew scattering,back scattering(reflection),side deflection scattering,and geometrical scattering,which depend on the VC polarity,the VC stiffness,structural symmetry of the vortex circulation, and the waveguide structure.Moreover,based on the asymmetric effect of chiral topological structure on scattering behaviors of SWs,a control scheme of SWs propagating in the cross-shaped nanostructure is proposed by reconstructing the chiral structure.
In order to investigate the effect of magnetic vortex chirality on the SW scattering behavior, the SW propagation in a cross-shaped ferromagnetic nanostructure is carefully explored by using micromagnetic simulations based on the Landau-Lifshitz-Gilbert equation.[38]In all the simulations,the material parameters of the permalloy are considered, the saturation magnetizationMS=8.6×105A/m, the exchange stiffness coefficientAex=13×10-12J/m,the Gilbert damping constantα=0.01,and the zero magnetocrystalline anisotropy.As schematically illustrated in Fig.1,the cross-shaped nanostructure is composed of two flat rectangular strips of 2000×200×2 nm3,overlapping each other,which is discretized into 106unit cells of 2×2×2 nm3.Initially,a magnetic vortex is set in the cross region of the nanostructure, as shown in two insets of Fig.1,which illustrates two chiral structures of vortex(1,1)and vortex(1,-1).All spins in the four arms of the nanostructure are initially set to point toward the cross center(see the white arrows)to form a stable magnetic vortex structure.An SW source is placed at the end of the left arm (arm 1),as the black part shown in Fig.1.The SW is excited by the sinusoidal microwave fieldBext=B0sin(2π ft)^z(^zisz-axis unit vector), withB0=200 mT andf=50 GHz.An original monochromatic SW(SWorg)propagates along the+x-axis direction from arm 1 to arm 3.To prevent the influence of SWs reflection from the ends,the high damping constant is set in the 30nm-width region(see gray parts)at the three ends of each arm(arms 2,3 and 4).
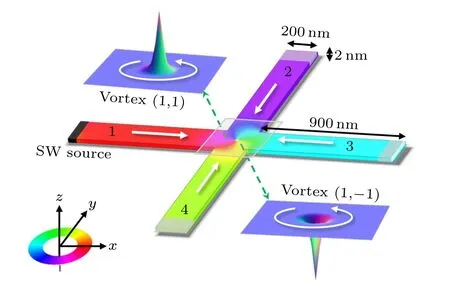
Fig.1.Geometry and dimension of the cross-shaped nanostructure in Cartesian coordinates.The color ring and white arrows indicate the inplane magnetization distribution.The black and gray parts show the positions of wave source and high damping regions, respectively.The upper-left and lower-right insets represent the right- and left-handed magnetic vortex structure,respectively.
As shown in Fig.2(a), it can be clearly observed that when the SWorgpropagates to the cross region of the nanostructure, the majority of the SWorgtravels through the vortex structure,and reaches arm 3,while a minority of SWorgis scattered to arms 2 and 4.As shown in Fig.2(b),there is a significant difference(asymmetry)in the average amplitudes of the SWs scattered into arms 2 and 4,whereas no such significant difference is observed in the no-vortex case(see Fig.S1 in the supplementary information).Hence,it can be found that there exists an interaction between the SW and the vortex, which suggests the occurrence of asymmetric behaviors in SW propagation.In addition, it is worth mentioning that in the vortex(1,1) case (see Fig.2(b)), the average amplitude of SWs injected into arm 2 is about 12 times larger than that injected into arm 4.
The asymmetric scattering of SWs is compared in the cases of four different chiral vortices [vortex (1,1), vortex(-1,1),vortex(-1,-1),and vortex(1,-1)]and the case without vortex(no-vortex)in order to verify the universality of the interaction between SW and vortex.As shown in Fig.2(c),the percentages of the average amplitudes of SWs scattered into arm 2(red)and arm 4(green)are compared in each case.In the no-vortex cases, the percentages of SW amplitudes for arms 2 and 4 are nearly identical, whereas in the presence of vortex structures,the percentages of SW amplitudes for arms 2 and 4 are noticeably different.It is obvious that the asymmetric scattering behavior of SWs in this system occurs due to the interaction between SW and vortex.It is worth reminding that the SWs scattered into arm 2 are relatively dominant when the VC polarity is up (p=1), while the SWs scattered into arm 4 are dominant when the VC polarity is down(p=-1).The change of vortex circulation (c=±1) does not significantly affect the asymmetric scattering effect.All of these reveal that the asymmetric scattering effect of the SWs in this system is mainly dependent on the VC polarity rather than the vortex circulation.
In order to further confirm the dominant role of VC polarity on the asymmetric scattering behavior of SWs in this system,a no-VC case was simulated in the redesigned nanostructure with an 8×8 nm2hole at the center of the cross region,as shown in Fig.3(a).The hole can pin the equilibrium point of the vortex circulation at the center of the cross region,and the vortex circulation structure still maintains symmetry[see inset of Fig.3(a)].The results show that the asymmetric scattering behavior of SWs cannot be observed in the no-VC case, as shown in Fig.3(b).However, by comparing the no-VC case and the no-vortex case[see Figs.3(b)and 3(c)],it can be clearly observed that the SW scattering effect in the no-VC case is more significant(~4.6 times)than that in the no-vortex case,and it is found that there is a phase difference(Δt ≈3 ps)between them,which suggests that the circulation structure of the magnetic vortex also has a scattering effect on the SWorg.In the no-vortex case,it can be clearly observed that the SWs are symmetrically scattered into arms 2 and 4, as illustrated in Fig.S1 of the supplementary information.The dispersion effect of SWs caused by the geometric characteristics of the waveguide structure can be called geometric scattering of SWs(SWgeo).[39]Therefore,it can be considered that the source of SWgeois located at the edges of both sides of the cross region.Obviously, in the no-VC case, the SWs scattered into arms 2 and 4 consist of two parts: one is the SWgeoand the other is the SWs caused by the vortex circulation scattering (SWC).Asymmetric scattering of SWs can also be achieved by modulating the vortex circulation structure,as shown in Fig.S2 of the supplementary information.
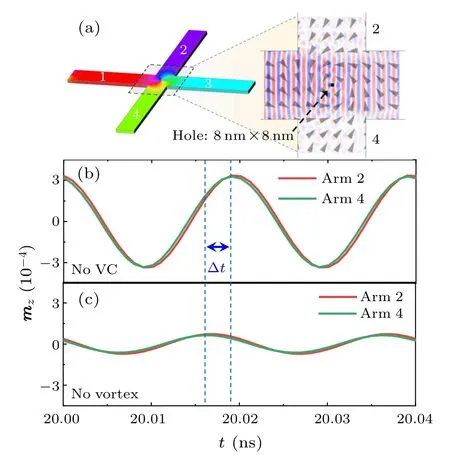
Fig.3.(a) Snapshots of SW distribution for the no-VC case at 20 ns after the SW excitation, the inset shows the magnetization distribution and SW distribution in the cross region.Time-varying mz signals collected at the detecting positions in arms 2 and 4, 550 nm far from the geometric center of the nanostructure,in the cases of(b)no-VC and(c)no-vortex.
The asymmetric scattering behavior caused by the interaction between SW and VC is an interesting physical phenomenon which belongs to the field of nonlinear science.In order to explore this phenomenon, the vortex (1,1) case was carefully analyzed in the following.In Fig.4(a), it can be clearly observed that 600 ns after the VC is excited by the SWorg,its gyromotion is effectively suppressed under the mechanical action of damping(FDM,red arrows),and finally converges(see the red time region)at a position~1.24 nm away from the cross center.This means that the SWorgalso has a skew mechanical effect on the VC, that is, an SW current force.[40]Although the VC deviates from the cross center under the SWorgcurrent force (FSW, the green arrow), it will not deviate further after~1.24 nm shift because there is a restoring force (FEP, the blue arrow) in this system that always points the cross center and its magnitude is related to the distribution of stray fields around the VC.Therefore, in this system the direction of theFEPis always opposite to theFSWwhile its magnitude is always equal to theFSWand depends on the distance(R)of the equilibrium position(EP)of the vortices from the cross geometric center.That is,the EP is determined byFEPandFSW.Nevertheless, after the equilibrium position of the vortex shifts a certain distance under the combined action ofFEPandFSW,the gyromotion behavior of the VC still follows the Thiele equation,[40-42]as shown by the dotted fitting line in Fig.4(a).The Thiele equation can be written as


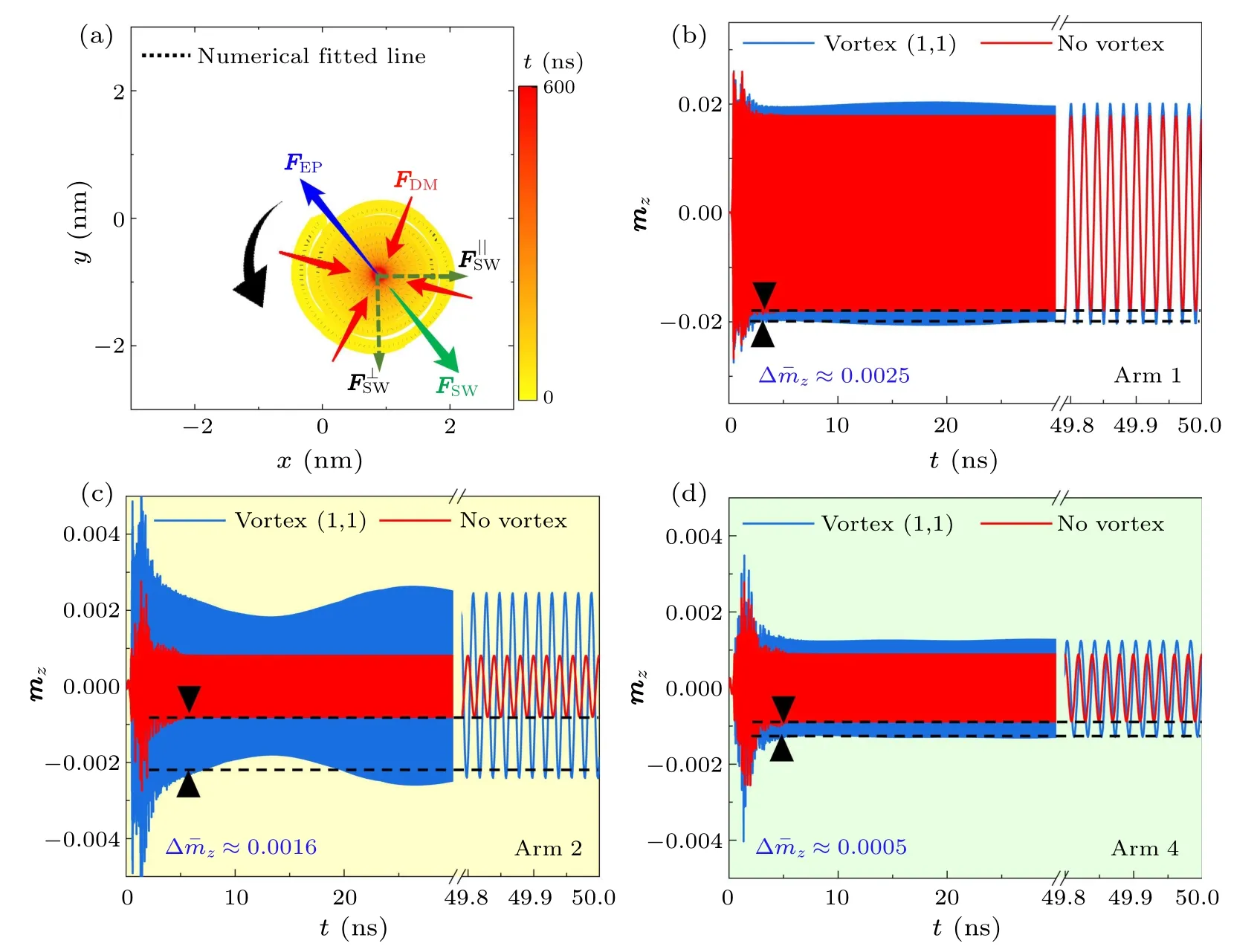
Fig.4.(a)The VC trajectory in the vortex(1,1)case during 600 ns,the black arrow represents the VC gyromotion direction and the red,blue and green arrows show the mechanical relationships among FDM,FEP,and FSW.Color bar indicates the time variation and the dotted line represents the numerical fitting.(b)The time-varying mz signals collected at the detecting positions 160 nm far from the geometric center of the nanostructure are shown in(b)arm 1,(c)arm 2,and(d)arm 4,for the cases of vortex(1,1)and no vortex.
In order to further confirm the possibility of SW scattering behavior caused by the reaction ofFSWon the VC, the distribution of SWs around the VC in the no-vortex and vortex (1,1) cases are compared.In the signals detected in arm 1, it is found that the mean amplitude of the signals in the vortex(1,1)case is obviously larger than that in the no-vortex case,Δˉmz ≈0.0025,indicating that the VC reflects the SWorgin the vortex (1,1) case, as shown in Fig.4(b).In the signals detected in arm 2, it is also found that the mean amplitude of the signals in the vortex (1,1) case is significantly larger than that in the no-vortex case, Δˉmz ≈0.0016, which is attributed to the skew scattering of the SWorgin the vortex(1,1)case,as shown in Fig.4(c).However,in the signals detected in arm 4,although the mean amplitude of the signals in the vortex (1,1) case is found to be larger than that in the no-vortex case, Δˉmz ≈0.0005, it is obviously weaker than that in arm 2(Δˉmz ≈0.0016).This means that the skew scattering effect of the VC on the SWorgobviously has asymmetric nature, as shown in Fig.4(c).According to the above phenomena, the conclusions are as follows: (1)The VC can cause reflection or skew scattering of the SWs.(2)The reaction forceFSWof the scattering or reflection will cause the oblique shift of vortex EP.(3)The skew scattering effect of VC on the SW is asymmetric and depends on the VC polarity(see Fig.S3 of the supplementary information).At present,the asymmetric interaction between VC and SW is considered originating from a socalled nonlinear topological magnon spin Hall effect, which is related to magnon spin-transfer torque effect[45-48]and depends on the magnon chirality and the VC polarity.However,the scattering behavior of vortex circulation structure on SWs has not received much attention so far,because the asymmetric scattering effect induced by vortex circulation structure is insignificantly compared with that of the VC,especially in the case of the SW driving the VC motion.In this paper,it is found that the vortex circulation structure contributes to the asymmetric scattering behavior of the SW and cannot be ignored.The obliqued shift of VC will make the vortex circulation distribution in the cross region of the nanostructure asymmetric,which will form an asymmetric scattering cross-section for the propagating SW,and eventually lead to asymmetric scattering effect.This conclusion is further confirmed by artificially designing a new micromagnetic simulation in which the vortex EP in the cross region is not located at the geometric center(see Fig.3(a)).
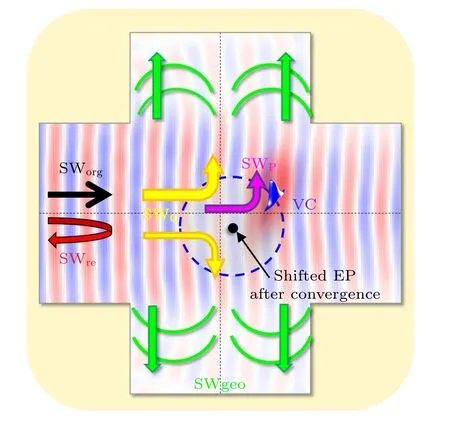
Fig.5.Schematic diagram of SW symmetric scattering mechanism for the SW propagating in the magnetic nonlinear system.The thick black arrow represents the SWorg propagating direction,the green arrows represent the geometric scatterings of SWgeo,the yellow arrows represent the SWC scatterings, the red curved arrow represents the SWre reflection,and the purple arrow represents the skew scattering of SWP.The red and blue interference patterns represent the main propagation distribution of SWorg.
In conclusion, it is found that there are four scattering mechanisms for SWs traveling in a cross-shaped ferromagnetic nonlinear system, as schematically illustrated in Fig.5:(i) the asymmetric skew scattering (SWP, purple arrow), related to VC polarity; (ii) the reflection (SWre, red curved arrow), associated with the scattering cross-section and stiffness of VC; (iii) the side deflection scattering (SWC, yellow arrows), depending on structural symmetry of vortex circulation; and (iv) the geometrical scattering (SWgeo, green arrows),depending on waveguide structural characteristics.The four mechanisms will play an important role in the exploration of nonlinear science and the development of magnonic devices.
Acknowledgments
Project supported by the Basic Science Research Program of the National Research Foundation of Korea (Grant No.2021R1F1A1050539), the Yanbian University Research Project(Grant No.482022104),and the Yichang Natural Science Research Project(Grant No.A22-3-010).
——記嘉蔭縣紅光鄉(xiāng)燎原村黨支部
- Chinese Physics B的其它文章
- Corrigendum to“Reactive oxygen species in plasma against E.coli cells survival rate”
- Dynamic decision and its complex dynamics analysis of low-carbon supply chain considering risk-aversion under carbon tax policy
- Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV
- Measurement of the relative neutron sensitivity curve of a LaBr3(Ce)scintillator based on the CSNS Back-n white neutron source
- Kinesin-microtubule interaction reveals the mechanism of kinesin-1 for discriminating the binding site on microtubule
- Multilevel optoelectronic hybrid memory based on N-doped Ge2Sb2Te5 film with low resistance drift and ultrafast speed

