Qi-Quan Li,Yu Zhang,Qian Li and Qi Sun

Faculty of Science,Kunming University of Science and Technology,Kunming,Yunnan 650500,China

Abstract We study the event horizon of a rotating Bardeen black hole surrounded by perfect fluid dark matter and the black hole as a particle accelerator.The black hole is represented by four parameters: mass M,rotation parameter a,dark matter parameter α and magnetic charge g.It is interesting that when we determine the values of magnetic charge g and dark matter parameters α we can get a critical rotation parameter aE and then we get a contour plane with Δ=0 taking three parameters as coordinates.We also derive the effective potential of the particle and the center-of-mass (CM) energy of the two particles outside the black hole by using the motion equations of the particle in the equatorial plane of the black hole.We find that the CM energy depends not only on the rotation parameter a,but also on the parameters g and α.We discuss the CM energy for two particles colliding at the black hole horizon in the extreme and non-extreme cases,respectively.It is found that the CM energy can become arbitrarily high when the angular momentum of one of the two particles is the critical angular momentum under the background of extreme black holes and there is no such result for non-extreme black holes,because the particles do not reach the black hole horizon when the angular momentum of the particles is critical angular momentum.Therefore,we prove that the rotating Bardeen black hole surrounded by perfect fluid dark matter can be used as a particle accelerator.

Keywords: black hole,particle accelerator,critical angular momentum,center-of-mass (CM)energy

1.Introduction

In April 2019,the event horizon telescope collaboration released the first image of a black hole shadow in Virgo A*.galaxy (M87),which lies 55 million light-years away from Earth [1].Just three years later,the collaboration officially published the first picture of the black hole shadow of Sgr A*located in the center of the Milky Way [2].The release of black hole shadows has given us an intuitive understanding of this mysterious celestial body in the Universe.However,there are still many problems in the theory of black holes,one of which is the singularity of black holes.In 1970,Hawking and Penrose proposed that when a spacetime satisfies the four physical hypotheses [3],it must be non-space-like and incomplete (i.e.there is a singularity).This means that when the mass of a star is greater than the Oppenheimer limit,it will collapse infinitely to form a black hole,and its matter will be compressed at the singularity of the black hole.The black hole singularity has a series of singular properties where the density and curvature are infinite,and the predictability of physical laws breaks down near the singularity.

In the real physical world,it is of great interest whether there is a singularity and whether there is a theory that can avoid the occurrence of black hole singularity.The existence of black hole singularity has not been verified by any experiments,but in theory,it is possible to prevent a black hole singularity from forming.In 1968,Bardeen [4] first proposed the regular black hole solution,which has a finite curvature scalar everywhere and no singularity.Borde discussed and analyzed the Bardeen black hole model in [5,6]and his study of black hole singularity further showed that in a large class of black holes,singularity can be avoided by topological changes [6].Ayón-Beato and García then found that in the framework of the standard general relativity,one can find a singularity-free solution of the Einstein field equations coupled to a suitable nonlinear electrodynamics,which is the charged version of the Bardeen black hole solution [7].Bambi and Modesto proposed the rotating Bardeen black hole [8].Recently,the metric of non-rotating and rotating Bardeen black hole surrounded by perfect fluid dark matter have been proposed and the shapes of Ergospheres have been painted [9].Of course,there are other regular black holes,such as the Hayward black hole[10]and the Berej–Matyjasek–Trynieki–Wornowicz black hole [11].

In order to study physical problems such as the origin of the Universe and the composition of matter,we built particle accelerators and particle colliders to accelerate particle collisions,but now we can only get particle collision energy less than 10 TeV,which is a huge gap with the energy corresponding to the physical theory that we need to verify and develop,such as the exploration of Planck-scale physics.Penrose indicated that black holes can provide a source of energy for surrounding matter [12].In 2009,Banados,Silk and West (BSW) [13] found that under the background of extreme Kerr black holes,when two particles with the same mass fall from infinity,if one of the particles has critical angular momentum,its center-of-mass (CM) energy is arbitrarily high when the two particles collide at the event horizon of the black hole.In [14],it was found that if a particle involved in the collision under the background of charged non-rotating Kaluza–Klein black hole has a critical charge,its CM energy will diverge at the horizon of the black hole,proving that non-extreme black hole can also be used as a particle accelerator.Patil and Joshi studied CM energy around naked singularities [15,16],and they successfully obtained a large amount of energy near the singularity.Since then,many different black holes have been demonstrated as particle accelerators [17–23].

In this paper,we mainly study the properties of particle collisions in the background of a rotating Bardeen black hole surrounded by perfect fluid dark matter,and the basic structure of this paper is as follows.In section 2,we review the rotating Bardeen black hole surrounded by perfect fluid dark matter and analyze the influence of dark matter parameter α,rotation parameter a and magnetic charge g on the horizon structure of black hole.In section 3,we calculate the equations of motion and effective potential of the particle on the equatorial plane of the black hole and discuss the range of angular momentum of the incident particle.In section 4,we derive the CM energies of two particles,and discuss the CM energies of particles at the event horizon of extreme and nonextreme black holes.In section 5,we summarize the content of the article.

2.Rotating bardeen black hole surrounded by perfect fluid dark matter

In this section,let us review the work of Zhang et al [9].In the Bardeen model,considering the coupling of gravity and nonlinear electromagnetic field,the corresponding Einstein-Maxwell equations should be modified as

where g and M are the magnetic charge and mass,respectively.Considering a black hole surrounded by perfect fluid dark matter,the energy-momentum tensor can be written as [25,26]

The black hole solution of the Bardeen black hole surrounded by perfect fluid dark matter can be obtained by solving the Einstein–Maxwell equations and energy momentum tensor as follows [9]:

In 1965,Newman and Janis proposed the Newman–Janis algorithm to solve the rotation of regular black hole [27],which has been widely used [25,28–35].The metric of the rotating Bardeen black hole surrounded by perfect fluid dark matter [9] was obtained by [36,37]For equation (8),when g=0,it recovers to the rotating Bardeen black hole metric [8],and when g=α=0,it recovers to the Kerr black hole metric [38].

We know that the Bardeen black hole has no singularity and is regular everywhere,but the question is whether the perfect fluid dark matter outside the black hole will affect this characteristic.Therefore,the curvature scalar of the black hole was calculated as [9]

When r=0,it is found in the above equation that the curvature scalar diverges due to the influence of the perfect fluid dark matter parameter α,indicating that there is a singularity in Bardeen black hole surrounded by perfect fluid dark matter.

2.1.Horizons

The metric (8) is singular at Δ=0 and corresponds to the horizon of black hole

From equations(12)and(13),when g and α take certain appropriate values,we can obtain aEthrough a numerical method,and then we draw a three-dimensional contour plane with Δ=0 in figure 3.By analyzing figure 3,we can find the following conclusions:

? We can obtain a region from the projection of the contour plane of Δ=0 on the g-α plane in figure 3.We find that any values of g and α in this region can find a aE(for a=aE,the black hole has a horizon and it is an extreme black hole),and when the values of g and α are not in this region,there is no aE.So in order to get an extreme black hole,the values of g and α must be in this region,and only in this region can aEexist.

? The three planes g=0,α=0,a=0 and the contour plane of Δ=0 form a spatial region.

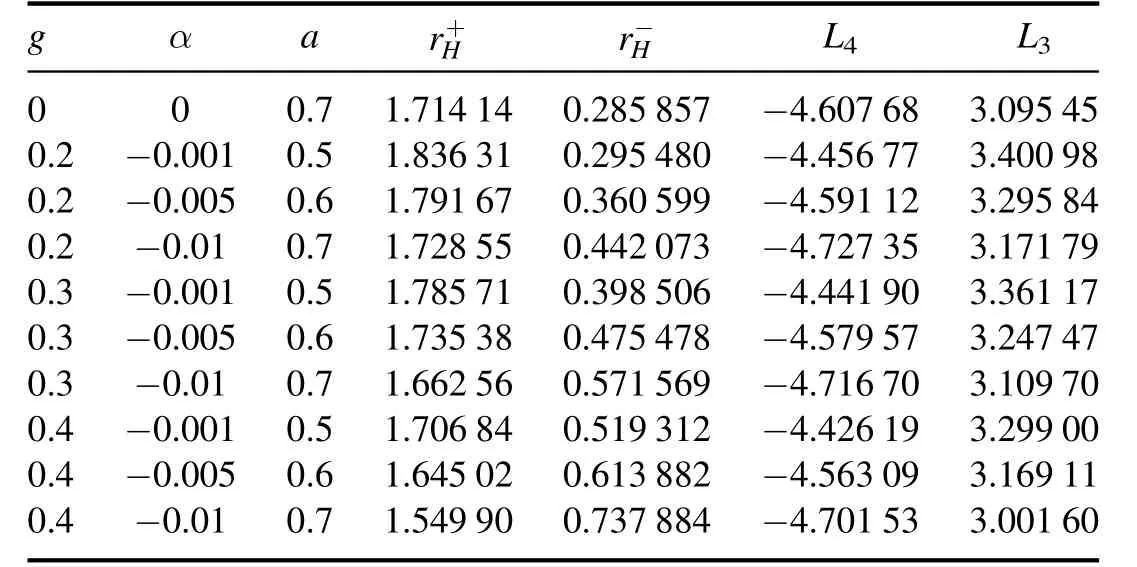
(1) The vertical coordinate a of the point in this spatial area satisfies a

(2) The vertical coordinate a of the point outside this spatial area satisfies a>aE,and Δ=0 has no root.There is no horizon in this particular case.

(3) When the vertical coordinate a of the point on the contour plane determined by Δ=0 satisfies a=aE,there is a root,and the black hole is an extreme black hole.

3.Equations of motion and the effective potential

In this section,we study the equations of motion for a timelike particle with rest mass m0in the background of a rotating Bardeen black hole surrounded by perfect fluid dark matter.We consider the particle moving on the equatorial plane of the black hole (θ=π/2,θ˙=0),and the generalized momentum of the particle in the space-time of the rotating Bardeen black hole surrounded by perfect fluid dark matter is expressed as follows:

we have an effective potential expression:

Fig. 2.Graphs of Δ versus r for fixed values of g=0.4 and M=1.Case a=aE corresponds to an extremal black hole.

Fig. 3.The contour plane of Δ=0,and the three coordinates are magnetic charge parameter g,dark matter parameter α and rotation parameter a,respectively.

The maximum and minimum angular momentum of the falling particle satisfy the following equation:

From the constraints of the above equation,we obtain the limiting values Lminand Lmaxof the angular momentum of the incident particles for extreme (table 1) and non-extreme(table 2) black holes.There is ut>0 for equation (16)because the geodesic of the particle is time-like,i.e.

When the above formula satisfies the conditionr→the following formula is obtained:

where ΩHis the angular velocity of the event horizon of the black hole,which is given by

Table 1.Limit values of angular momentum for different extreme values of a rotating Bardeen black hole surrounded by perfect fluid dark matter.

The critical angular momentum Lc=E/ΩHis obtained when we take the equal sign of equation (23).In figure 4 we give the curves of urversus r for different values of L,a,g and α.As can be seen from the figure,if the particle has a large angular momentum L>Lc,the geodesic do not fall into black holes.On the other hand,if the angular momentum L

Fig. 4.The behavior of ur versus r for extremal black hole.

Table 2.The limiting values of angular momentum for different non-extremal cases of rotating Bardeen black hole surrounded by perfect fluid dark matter.

4.Near horizon collision in rotating Bardeen black hole surrounded by perfect fluid dark matter

In this part,we calculate the CM energy of two time-like particles outside the black hole,and discuss the conditions under which the CM energy of two particles colliding at the horizon of the black hole will diverge.

For two time-like particles moving on the equatorial plane of the black hole,we take the particles mass m1=m2=m0,energy E1=E2=1,angular momentum L1and L2,respectively.The four momentum of particle i (i=1,2) is

For two particles the CM expression is

By using particle four-velocity normalization uνuν=-1,the above formula can be simplified to

Fig. 5.The behavior of Veff versus r for different angular momentum L.

Fig. 7.The behavior of ECM versus r for non-extremal black hole.

Fig. 8.The left and right graphs represent the corresponding ECM versus r images when changing the values of parameter g and a,respectively.

We substitute equations (16)–(18) into the above equation to simplify

From the above equation,we can draw that there are two major types of parameters affecting the CM energy of the two particles.The first type of parameters is related to the nature of the black hole itself,namely a,g and α;the second type of parameters is related to the physical quantity of the particle,namely L and m0.Of course,the CM energy is also affected by the radial coordinates of the two particles.We can adjust the parameters in equation(29)to make the CM energy of the two particles diverge at the event horizon of the black hole.Nonetheless,the former type of parameters is the property of the black hole itself and we cannot change it,so we can consider the second type of parameters.But in the latter parameters,adjusting the mass of the particle obviously cannot make the CM energy diverge,so we can adjust the angular momentum of the two particles.Therefore,we are inspired to discuss whether it is possible to make the CM energy arbitrarily high by adjusting the angular momentum of the two particles when they reach the horizon of the extreme or non-extreme rotating Bardeen black hole surrounded by perfect fluid dark matter.

For extreme black holes,the inner and outer event horizons coincide.Figure 6 shows the behavior of EMCversus r for extreme black holes with different parameters g and α.From the figure,we can get a conclusion that when one of the two particles of the incident particle has critical angular momentum,the CM energy diverges near the event horizon of the black hole,while the particle with LLccannot reach the event horizon of the black hole.

For non-extreme black holes,the inner and outer event horizons are separated,and figure 7 shows the behavior of Ecmversus r for non-extreme black holes with different parameters g,a and α.Ecmdiverges at the event horizon under the condition that the angular momentum of the particle satisfies a range determined by equation (21) and the angular momentum of a particle is the critical angular momentum.But at this time,it is found that the critical angular momentum is not satisfied with the angular momentum range of the particle falling into the black hole,so Ecmdoes not diverge.For example,when g=0.3,α=-0.005 and a=0.7,the range of angular momentum is-4.659 33–3.052 11,and the critical angular momentum is 4.501 16.The latter value is not satisfied with the angular momentum range of the particle falling into the black hole,so the CM energy does not diverge.Finally,in figure 8,we draw the curves of Ecmversus r corresponding to different values of magnetic charge parameter g and perfect fluid dark matter parameter α,respectively.We find that when the magnetic charge parameter g is in the range of 0.2–0.8 and the perfect fluid dark matter parameter α is in the range of -0.01 ～-0.001,the CM energy increases with the increase of the two parameter values.

5.Conclusion

In this paper,we have studied the event horizon of a rotating Bardeen black hole surrounded by perfect fluid dark matter,and have analyzed its possibility as a particle accelerator by studying the CM energy of two particles falling freely from infinity.The event horizon structure of the rotating Bardeen black hole surrounded by perfect fluid dark matter is more complex than that of the Kerr black hole and the rotating Bardeen black hole.We have found that when g and α are determined,one can get the critical value aE,which corresponds to the extreme value of a degenerate horizon black hole,that is,when a=aE,the two horizons coincide,and when aaE,the black hole horizon does not exist.

We have used the BSW mechanism to obtain the expression of the CM energy of two particles colliding in the equatorial plane of the black hole and have discussed its properties.Through the conservation of energy and angular momentum of the particle and the four-speed normalization of the particle,the equations of particle motion,and the value range of angular momentum of the particle are obtained.We have calculated the expression of particle CM energy and have discovered that CM energy for extreme black holes will diverge when one of the incident particles has critical angular momentum.Nevertheless,in the case of non-extreme black holes,the CM energy is limited,because one of the two particles with critical angular momentum cannot reach the event horizon of the black hole,and its angular momentum does not satisfy the angular momentum range of the particle falling into the black hole.For particles that can be incident into a non-extreme black hole,the CM energy depends on the magnetic charge parameter g,the dark matter parameter α,and the rotation parameter a,so the BSW mechanism depends on those parameters as well.

After Penrose proposed the Penrose process[12]in 1971 and the BSW mechanism proposed by Banados,Silk,and West [13] in 2009,Bejger et al [40] utilized the BSW mechanism to improve the energy extraction efficiency of the Penrose process.In [41],the BSW mechanism is used to accelerate particles and the Penrose process to extract energy,and it is found that the efficiency of Compton scattering between photons and massive particles near the event horizon can reach nearly 1400%.It has been shown in many studies[42–44] that the energy extraction efficiency of the Penrose process using the BSW mechanism is much higher than that of the Penrose process alone.This indicates that the BSW mechanism plays a significant role in particle acceleration,black hole energy extraction,and Planck scale physics research.In future work,we hope to use the BSW mechanism to study the Penrose process and calculate the maximum efficiency of energy extraction under the background of rotating Bardeen black holes by perfect fluid dark matter.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No.12065012),Yunnan Fundamental Research Projects (Grant No.202301AS070029),and Yunnan High-level Talent Training Support Plan Young and Elite Talents Project (Grant No.YNWR-QNBJ-2018-360).