Matthias Baaz Norbert Preining

Abstract. This paper introduces diagrams in projective geometry as valid proving tools.Al though diagrams are used to support the understanding of proofs in projective geometry,they are not considered as proofs themselves.We will show that diagrams can be transformed in cut free proofs with elementary expense and vice versa.This means,that diagrams are a valid and complete proof tool,however diagrams may be non elementarily more complex than usual proofs using lemmata(cuts).As an interesting consequence of these analyses we will demon strate,that diagrams are not constructive in the logical sense.

1 Introduction

What is our way of proving? Which ways of demonstrating the truth of a state ment are accepted as proof? What is the connection between informal descriptions and formal proofs,is there any at all?

Over time various proof methods have emerged and fallen back into oblivion.A lot of these lost methods were used to guide mathematicians into new areas of knowledge,assure them of the truth of their conjectures.To cite from[19]:

We secure our mathematical knowledge bydemonstrative reasoning,but we support our conjectures byplausible reasoning.A mathematical proof is demonstrative reasoning,but the inductive evidence of the physi cist,the circumstantial evidence of the lawyer,the documentary evidence of the historian,and the statistical evidence of the economist belong to plausible reasoning.

The difference between the two kinds of reasoning is great and man ifold.Demonstrative reasoning is safe,beyond controversy,and final.Plausible reasoning is hazardous,controversial,and provisional.Demon strative reasoning penetrates the sciences just as far as mathematics does,but it is in itself(as mathematics is in itself)incapable of yielding essen tially new knowledge about the world around us.Anything new that we learn about the world involves plausible reasoning[…]

Accompanying the introduction of formal methods within mathematics and logic less and less methods of proving where founded on a formal base and therefore ac cepted as valid.One particular interesting example,and at the same time one of the last ones,since it is from 1953,is the use of physical notions in a proof of Schütte([26]),which would be impossible today.Nevertheless it is of fundamental proof theoretic interest to understand the relation between formal proofs and informal descriptions.If we improve our understanding of these connections we could on the one hand bet ter understand old proofs using these methods and on the other hand really use this methods in new proofs.

The use of diagrams in geometry resembles exactly the description given above.They were used for plausible reasoning ([19,20]).Ever since ancient civilizations like the Chinese,Arian or Greek cultures started to prove geometrical theorems there where different forms of proving,different ways of assuring the truth of statements.All these different forms where accepted as complete proving tools.The distinction between plausible and demonstrative reasoning has not been made.With the begin ning of strict formalization of mathematics and the use of formal methods within mathematics,some of these proving techniques have vanished or have changed the way they are used,because they couldn’t meet the requirements of current science for a valid proving method.Some of these methods still exist but have lost there im portance because they where not considered “timely” or formal enough to be used,see[13]for discussion and further references.

One of these methods is the use of diagrams to prove facts of various geometries.This method has had a long history as we will point out below.We will undertake a small excursion in the history of diagrams and try to investigate this very old method of proving.In this paper we will analyze diagrams within the framework of proof theory to understand the connection between diagrams and formal proofs.

In recent times diagrams have lost their status as proving tool.The purpose of this paper is to show that diagrams can be regarded as proofs,i.e.that we can translate diagrams into proofs and vice versa.Additionally we will show interesting results concerning the length of diagrams compared to the length of proofs using standard techniques like cut elimination.For this purpose we will use Herbrand disjunctions,which will be analyzed in detail in Section 4.

1.1 Historic examples

Proofs of geometric propositions are found in the earliest known mathematical texts in India and China as well as in Greece.Let us give some examples (taken from[31]):

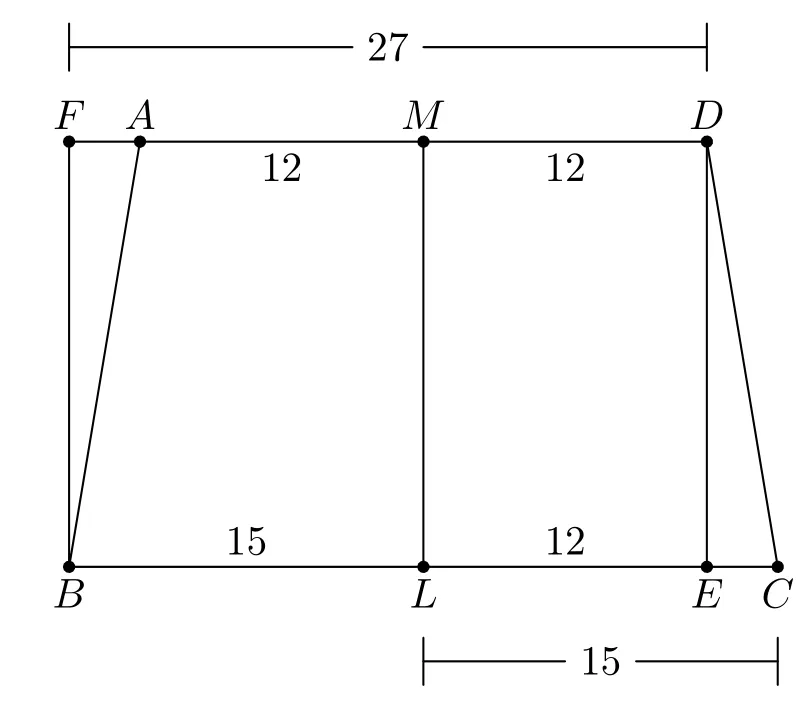
Figure 1:Area of a trapezium

One draws(a line)from the southernamsa(Din Figure 1)toward the south ern srōni (C),(namely) to (the pointEwhich is) 12 (padasfrom the pointLof theprsthya).Thereupon one turns the piece cut off(i.e.the triangleDEC)around and carries it to the other side(i.e.the north).Thus thevediobtains the form of a rectangle.In this form(FBED)one computes its area.

The translation is taken from [27,p.332],where there is also an interesting comment:

The striking thing is that here we have a proof.

As another example let us present a passage from the earliest Chinese text on astronomy and mathematics,theChou Pei Suan Ching,which may be translated as“Arithmetical Classic of the Gnomon and the Circular Paths of Heaven.”In this clas sical text from the Han period a proof of the“Theorem of Pythagoras”is presented.The proof is only worked out for the (3,4,5) triangle,but the idea of the proof is perfectly general.Figure 2 and the translation are taken from[16]:

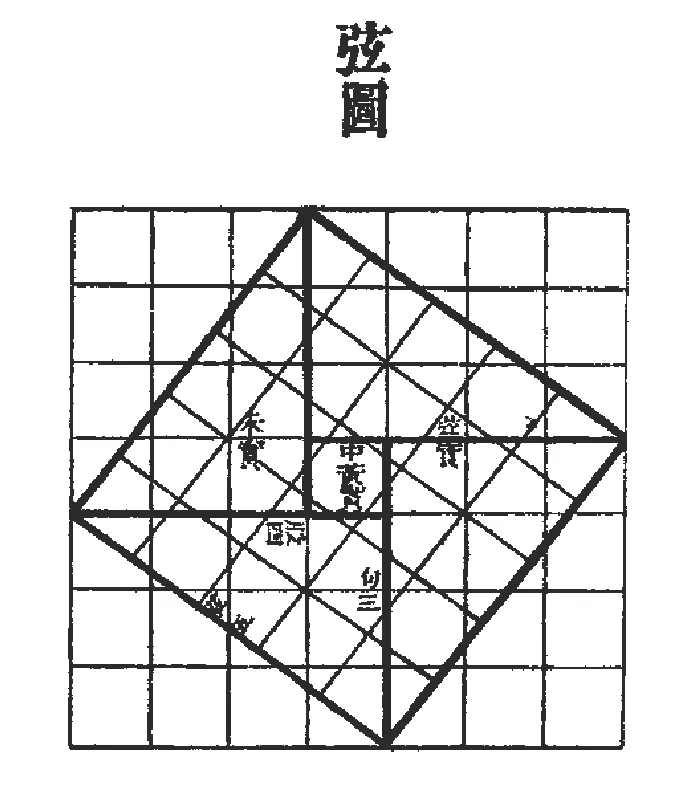
Figure 2:The proof of the Pythagorean Theorem in the Chou Pei Suan Ching.From J.Needham:Science and Civiliza tion in China,Vol.3

Thus,let us cut a rectangle(diagonally),and make the width 3(units)wide,and the length 4(units)long.The diagonal between the(two)corners will then be 5(units)long.Now after drawing a square on this diagonal,circumscribe it by half rectangles like that,which has been left outside,so as to form a(square)plate.Thus the(four)outer half rectangles of width 3,length 4,and diagonal 5,together make two rectangles (of area 24)? then (when this is subtracted from the square plate of area 49)the remainder is of area 25.This(process)is called“piling up the rectangles.”

These examples are of course not the only ones.All the proofs in Euclid’s“El ements”can be viewed as diagrams.But diagrams as proving tools are not limited to ancient times,there are a lot of theorems in geometry which are obvious from a dia gram,take for example Dandelin’s theorem([17])on the intersections of a plane with a cone or Robert’s theorem on the existence of triangular faces in the arrangement of lines in an Euclidean plane.Other examples in logic can be found in the works of C.S.Peirce,see[12].

1.2 Current state

Today diagrams lost most of their importanceas proving tools by themselvesand are more or less only used to explain the ideas of a proof and to help understanding,but all the proofs have to be formalized in a strict sense.On the other hand there are some approaches to the area which try to reintroduce diagrams as proofs:For example,Grünbaum introduced a notion of provability in elementary geometry which is based on diagrams made with MATHEMATICA([33]).Other approaches of proving with the help of diagrams can be found in programs likeGeometer’s Sketchpad([30])orDrGeo([10]).

(Projective)Geometry is also the topic of research in automated reasoning([9,32,34]),formal verification([7,8]),and related works([5,6]).

1.3 Why projective geometry

Projective geometry is the simplest geometry,since the only concept is inci dence,i.e.“point lying on a line”,while other geometries,like affine or even higher geometries introduce more and more concepts like parallel,distance,measurement.But although projective geometry lacks concepts like distance and angle,it has great expressive power(cf.Section 6).

One step of making a diagram is to assume points or lines in a“general”position.This means that a new point should not be placed in some special relation to the other ones.Given how many“special”points there are in a triangle,it is obvious that it is difficult to put a new point into it which is“for sure”not one of these special points.In projective geometry the assumption of general position is easier,just because of this lack of higher concepts.

Finally we want to mention that projective geometry is also easily axiomatized,it is in fact defined by only three axioms.

2 Diagrams in Projective Geometry

Most of the proofs in projective geometry are illustrated by a diagram.In gen eral,a diagram in projective geometry is considered only as tool to support the un derstanding of a accompanying formal proof,exhibiting basic facts about incidences and equalities.

In this paper we want to show that diagrams,due to the minimality of projective geometry with respect to predicates(only incidence and equality),can be considered proofs by themselves,and by this are open to proof theoretic analysis.

2.1 Introduction to projective geometry

2.1.1 What is projective geometry

Definition 1(LPG).The language for projective geometry has two types calledPointsandLines1We will use the expression“Point”(note the capital P)for the objects of projective geometry and“points”as usual for e.g.a point in a plane.The same applies to“Line”and“l(fā)ine”.,variables of these types(P,Q,…for Points,g,h,…for Lines),equality(=),incidence(I,arity two,type(Point,Line)),and two function symbols con(arity two)and intsec(arity two),and for constants,the PointsA0,B0,C0,D0.

Terms of the language are con(P,Q)whereP,Qare of type Point,and intsec(g,h)whereg,hare of type Line.These terms will be also written as[PQ]and (gh) re spectively.The former one is of type Line,the latter on is of type Point.

The atomic formulas of the language are equalities between terms of the same type andP I gwherePis a Point andgis a Line.

The axioms for projective geometry are

or in more common terms

? (PG1)For every two distinct Points there is one and only one Line,so that these two Points incide with this Line.

? (PG2)For every two distinct Lines there is one and only one Point,so that this Point incides with the two Lines2“one and only one”can be replaced by“one”,because the fact that there is not more than one Point can be proven from axiom(PE1)..

? (PG3)There are four Points,which never incide with a Line defined by any of the three other Points.

2.1.2 An example:the finite projective plane

One of the basic properties of projective planes is the fact that there are seven distinct Points.Four Points satisfying axiom (PG3) and the three diagonal Points([A0B0][C0D0])=：D1,([A0C0][B0D0])=：D2and ([A0D0][B0C0])=：D3.If we can set up a relation of incidence on these Points such that the axioms(PG1)and(PG2)are satisfied,then we have a minimal projective plane.Figure 3 defines such an incidence table.In this table not only the straight lines are Lines for the projective geometry,but also the circle.

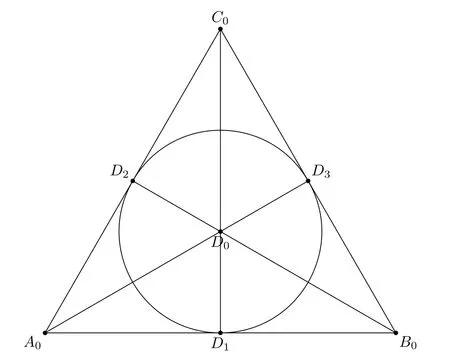
Figure 3:Incidence Table for the minimal Projective Plane

We could attribute a number called“order”,which is the number of Points on a Line minus one,to every finite projective plane.Then there is the question for which numbernthere is a projective plane with ordern.One partial solution of this problem depends on the existence of finite fields.Given a finite field,we can construct a finite projective plane with the same order.Since there are finite fields for every power of a prime3The so called Galois Field GF(n).,for any such number there is also a projective plane.

Principally these questions can be answered simply by trying all possible relation tables withnPoints andnLines and check whether there is one satisfying the axioms.But this method is computationally infeasable,because the number of such tables rises exponentially.

2.1.3 Some consequences of the axioms

We want to mention some consequences from the axioms which are easily prov able:

? There are seven distinct Points in a projective plane,namely the four constantsA0,...,D0and the three diagonal Points

? For each Line there are three distinct Points which incide with this Line.

? For distinct Linesgandhthere is a PointPsuch thatand.

? There is a one to one mapping from the set of Points to the set of Lines in a projective plane.

? If there are exactlyn+1 distinct Points on a Line,then on every Line there aren+1 distinct Points,for each Point there are exactlyn+1 different Lines passing through it and there are exactlyn2+n+1 Points and exactly that many Lines.

2.2 A formalization of diagrams in projective geometry

In this part we give a formalization of a diagram in projective geometry and explain our motivation behind some of these concepts.

All Points and Lines are combined in the sets calledτPandτL,respectively.So if we say,thatx ∈τP,then we mean thatxis of type Point,i.e.it’s any term which describes a Point.

Diagrams speak about geometric objects,that are Points and Lines.So the first logical objects necessary for the formalization are constants or variables for Points and Lines.From these constants we build more complex objects by connecting and intersection.This step is described in the following definition.

Definition 2(Set of Terms overC).LetCbe a set of constants of typeτPorτL,thanTnis inductively defined

Definition 3(Depth).Thedepthof a termtis defined as the numbern,at whichtis added(or constructed)in the process given above.

The expression“depth”describes how deeply a term is nested.

A simple condition on a subset ofT(C)is the property to be closed under sub terms:

Definition 4(admissible set of terms).LetMbe a subset ofT(C),Ca set of con stants,thenMis called admissible if it obeys the following rules:

The idea is to define a set of Points,Lines and certain combinations of them(the intersection points and connection lines)and let the diagram be a subset of all possible atomic formulas over these terms.

Definition 5(Universe of Formulas).LetMbe an admissible set of terms andPa set of predicates,then the universe of formulas overMwith regard toPis defined as

With?FUP(M)we denote the set of all negated atomic formulas fromFUP(M),i.e.

In the following,Pwill only be{I,=}or{I}.The setFUcontains all the possible positive statements which can be made over the set of termsM.

In the course of a formal construction a special situation can occur that has to be resolved immediately,as it describes a situation where same objects have different names:

Definition 6(Critical Constellation).LetPandQbe terms inτPandgandhterms inτL.Then we call the appearance of the following four formulas a critical constel lation:

We will denote such critical constellations by(P,Q;g,h).

Such a constellation is called critical,because from these four formulas it follows that eitherP=Qorg=h(or both),but we cannot determine which one of these alternatives holds without supplementary information(see Figure 4).

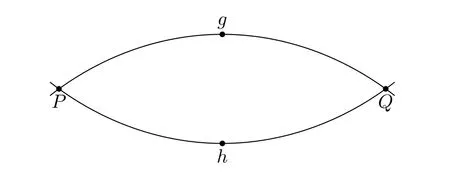
Figure 4:The two solutions for a critical constellation

When constructing any diagram we start from some assumptions over a set of constants and then construct new objects and deduce new relations.From a proof theoretic point of view these first assumptions are the left side of the deduced sequent,i.e.the assumptions from which we deduce the fact.

We want a diagram to be a set describing all the incidences in the diagram4This one is on the paper!.But we also want that this subset is closed under trivial incidences,which means that if we talk about a Line which is the connection of Points,then we want that the trivial formulas express that these two Points lie on the corresponding Line.

Further we don’t want to have a critical constellation in a diagram.That’s be cause we want that every geometric object is described by only one logical object,i.e.one term.Since a critical constellation implies the equality of two logical objects,without and automatic way to determine which pair,we want to exclude such cases.

Definition 7(Diagram).LetMbe an admissible set of terms over a set of constantsCwhich contains all constants and lines generated from the constants,i.e.

letEbe a subset ofFU{I}(M)∪?FU{I,=}(M)with

letQbe a set of equalities and let the triple(M,E,Q)obey the following require ments:

Then we call the tripleS=(M,E,Q)a diagram.

We will call the violation of(S.2)also a direct contradiction.

A small example should help to understand the concepts:

In the diagram depicted in Figure 5 the different sets are(incidences of the con stants not listed):

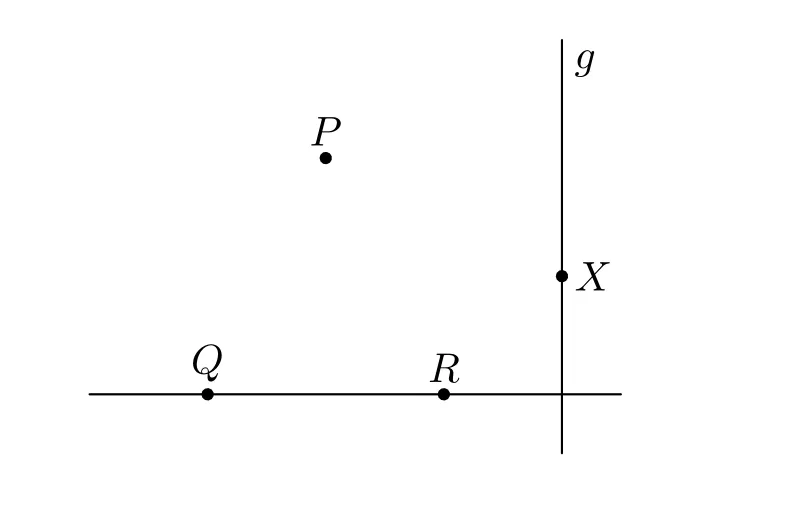
Figure 5:A sample diagram

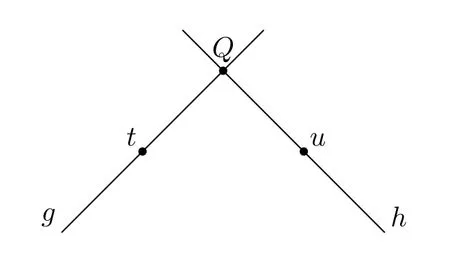
Figure 6:Identifying two objects t and u

By convention,expressions likeP ∈S,(P I g)∈S,()∈S...,mean,respectively,P ∈M;(P I g),()∈E.Any other similar expression has to be interpreted accordingly.

Why should the setEbe a subset only ofFU{I}(M)and not ofFU{I,=}(M)?The reason is that in a diagram every geometric object should have one and only one name and should also be described by one logical object.The same idea lies behind the introduction of the concept of the critical constellation.

Note that one diagram is only one stage in the process of a construction,which starts from some initial assumptions and by constructing diagrams successively,de duces more and more facts and so constructs more and more complex diagrams.

The setQin the definition of the diagram was initially absent,but investigations in the equality of proofs and constructions showed that this set is important for the proof,although it is not used in the diagram.This depends on the usage of equality:in the diagram it is a strict one,i.e.,there is only one name for an object allowed,while in a proof you can use at some point one name and a different name at another point.In the diagram,as we will see later,there is not a local substitution of a term,but a global one,therefore only one name is“actual”at a time for an object.But if we want to translate a proof into a construction,which is one of the aims of this work,we need information on all the name changes that are possible.

2.3 Actions on diagrams

Till now a diagram is only a static concept,nothing could happen,you can not “construct”.Thus,we define certain actions on diagrams which result in new diagrams with more information.These new diagrams need not satisfy the require ments(S.1)–(S.3),but it will be asemi diagram:

Definition 8(Semi diagram).Asemi diagramis a diagram that does not need to satisfy(S.2)and(S.3).

These actions should correspond to similar actions in real constructing.After these actions are defined,we can explain what we mean by a construction in this calculus for construction.

The following list defines the allowed actions and which special actions have to be taken in a specific step by describing the changes that have to be carried out on the triple of a diagram.

In the following listing we will use the function closure(Q)on a set of equalitiesQ.This function deduces all equalities which are consequences of the setQ.This is a relatively easy computation.If we haveQ={x=x,y=y,z=z,x=y,y=z},then the procedure returnsQ ∪{x=z}.This function is used to update the setQof a diagram after a substitution.

Joining of two PointsX,Y?Symbol:[XY]

The requirement (S.1) and (S.4) is fulfilled since the necessary formulas are added toEandQ.This action can produce a semi diagram from a diagram.

Intersection of two Linesg,h?Symbol(gh)

Dual to the joining of two points.

Assuming a new ObjectCin general position,Symbol{C}

ThatS′is a diagram is trivial,sinceCis a completely new constant.Cmust be a constant of typeτPorτL.

Giving the Line[XY]a nameg：=[XY]?Symbolg：=[XY]

S′is a diagram since this operation is only a name change.

Giving the Point(gh)a nameP：=(gh)?SymbolP：=(gh)

Dual to giving an intersection point a name.

Identifying two Pointsuandt?Symbolu=t

Note that the setQ′can contain termstnot inM′.This action can produce a semi diagram from a diagram.

Identifying two Lineslandm?Symboll=m

Dual to identifying two Points.

Using a“Lemma”:Addingt I u?Symbolt I u

This action can produce a semi diagram from a diagram.

Adding a negative literalt I| u?Symbol

Adding a negative literaltu?Symboltu

To deduce a fact with diagrams we combine the concept of diagram and the concept of actions into a new concept called construction.Construction will deduce facts.

Definition 9(Construction).Aconstructionis a rooted and directed tree with a semi diagramSattached to each node and an action attached to each vertex and satis fying the following conditions:If a vertex with actionAleads from nodeN1to nodeN2,thenN2is obtained fromN1by carrying out the action onN1.If from a nodeNthere is a vertex labeled…

? with[XY]or(gh),thenXYorghis contained inEN.

? with{C},g：=[XY],P：=(gh),then there is no other vertex fromN.

? withP I g,P I| g,X=Y,XY,then there is exactly one other vertex labeled with the negation of a formula.This is called a case distinction.

Furthermore ifSattached to a node…

? yields a direct contradiction,then it has no successor,

? is a semi diagram but not a diagram,i.e.that there are critical constellations,let(P,Q;g,h)be one of them,then there are exactly two successors,one labeled with the actionP=Qand one labeled with the actiong=h.

What is deduced by a construction:A formula is true when it is true in all the models of the given calculus.The distinct models in a construction are achieved by case distinctions.So if a formula is deduced by a construction,it must be present in all the leaves of the tree.Since some leaves end with contradictions(from which we can obtain anything),we require only that a formula,which should be deduced,has to be present in all leaves which are not contradictory.

We also have to pay attention to the way a construction handles identities.Since in a construction an identity is carried out in the way that all occurrences of one term are substituted for the other,we prove not only an atomic formula,but also all the formulas which are variants with respect to the corresponding setQ.This notion will now be defined.

Definition 10.Two atomic formulasP(t1,u1)andP(t2,u2)are said to beequiv alent with respect to Q,whereQis a set of equalities,in symbolsP(t1,u1)≡QN P(t2,u2),when(t1=t2),(u1=u2)∈QN(or the symmetric one).

Now we can define the notion of what a construction deduces:

Definition 11.A construction deduces the formula

The meaning of this definition is that if a construction deduces ?then the dis junction of all formulas in ?is proved by this construction.

3 Overview and Layout

We want to show the equivalence of constructions(as defined in Section 2)with formal proofs in the sense that for any formulaAprovable in Projective Geometry,we can give a construction which proves the same formula and vice versa.

We will start with formulaAprovable in Projective Geometry

which is nothing else than

whereAxis the set of axioms for Projective Geometry.Note that these axioms contain existential quantifiers.Next we will skolemize this formula as shown in Section 4 and obtain

This Skolem form does not contain strong quantifiers(see Definition 13)and thus we can obtain a Herbrand Expansions(see Section 4.1)for this formula,which we will denote with

We will use a special procedure to transform this propositional formula into an equiv alent one which is–in a certain sense–minimal.The discussion of this minimality is done in 4.2.We obtain

To make a construction from this formula we have to eliminate the Skolem func tions which have been introduced in the above process.This will be explained in Section 4.3,arriving at

which is a purely propositional formula not containing any Skolem function.From this we can generate a construction as shown in Section 5.

This completes the extraction of proofs from diagrams.

We continue in Section 6 with proving that there are formulas which can be proven by construction,but the difference in length of proof by construction and by LK increases non elementary.Herein we use Orevkov’s result([18])and adapt it to Projective Geometry.

4 Herbrand Expansions

In his thesis from 1930,Jacques Herbrand proved the fact that for all provable formulas of first order predicate logic an equivalent one without quantifiers can be found.This insight,today called Herbrand’s theorem,is one of the most fundamental of mathematical logic,since it allows the discussion of the validity of any formula just in terms of finite means,i.e.,in terms of propositions,and not in terms of the abstract notation of quantifiers.

In the previous part we have defined a notion of provability in Projective Geom etry using constructions.Now we want to follow the path laid out in Section 3 and develop a method for the transformation of a provable formula into a construction which proves this formula.The first step as given in Section 3 is the skolemization of the formulaAwith the axioms prefixed,i.e.,ofAx ?A,whereAxis a conjunction of axioms of Projective Geometry.

In the following we willnotrestrict ourselves to prenex formulas.Note that prenexation changes the Herbrand expansion,an underlying reason for the errors in Herbrand’s original proof.In Projective Geometry,we will often have to work with formulas of the following form

Later on we will present Herbrand’s theorem in its original form,which is dif ferent from the one dominating the current use,where a slightly different form,calledSkolem form,appears.This Skolem form is more suitable for resolution techniques and automated reasoning.

Definition 12(sign of a quantifier).Thesignof a quantifier within a formula is defined as follows:The sign of the quantifier inQxA(x)is positive.The sign of the quantifier changes when going fromAto?Aand fromAtoA ?B.The sign does not change in any other case.

As an example take the following formula

The universal quantifier is in the scope of one negation sign and in the left scope of one implication,therefore the sign of this quantifier is positive.The existential quantifier is in the scope of one negation and its sign therefore is negative.

Definition 13(strong,weak).A quantifier is calledstrongif it is a universal quan tifier with a positive sign or a existential quantifier with a negative sign.Otherwise it is calledweak.

We will associate a closed formulaS(A) with each closed formulaAwhere every strong quantifier is replaced by a Skolem term depending on weak quantified variables of its scope.

More formally we transform the formula into a tree in the following way:

Definition 14(tree associated with a formula and term).The tree of a constant or variable is a single node with this constant attached.The tree of a term is a node with the function symbol attached and,ifnis the arity off,nsuccessors with the trees of the subterms are following.The tree of an atomic formula is a node with the predicate symbol attached and,ifnis the arity ofP,nsuccessors with the trees of the terms are following.The tree of a formulaA ∧Bis a node with∧attached and 2 successors with the trees forAandBare following.The trees for∨,?and?are similar.The tree for a formula(Qx)A(x)is a node with(Qx)attached and one successor with the tree ofA(x).

Letnbe a node within this tree.Then the path from the top to this nodenis written aspn.If a strong quantifier is attached to this node,we compute two numbers for this node:One is the number of weak quantifiers and one is the number of strong quantifiers on the pathpn.We will write these two numbers asn(e,u).In other words:If we have a node labeled withn(e,u)then a strong quantifier is attached to this node,there areeweak quantifiers andustrong quantifiers on the path from the top to the noden.

Now we transform the path several times by the same procedure:If there is no noden(e,0)then there is no strong quantifier at all and we are finished.Otherwise take one of these nodes,a new function symbolfwith aritye.Now substitute within the subtree starting from the nodenall occurrences of the variable for the universal quantifier with the termf(x1,...,xe),where thexiare the variables from theeweak quantifiers on the pathpn.Finally remove the nodensince all the variables bound by the respective quantifier are already substituted and recompute the valueseandufor all nodes with strong quantifiers in this subtree.

After repeating this process a finite number of times we obtain a tree without any strong quantifiers which we can transform back into a formula,which we will call the Skolem form of the original formulaA,written asS(A).

Example.LetAbe the formula

It is not too difficult to show the following lemma:

Lemma 1.A formula A is provable if and only if S(A)is provable.

4.1 Herbrand expansions

Herbrand disjunctions are a well known tool,but require prenexation.The orig inal form of Herbrand’s Theorem does not require prenexation but works with infix formulae.To keep axioms and consequences separate in Projective Geometry,we will use infix formulae.For this,the usualHerbrand disjunction(a disjunction of instances of the matrix)need to be exchanged withHerbrand expansions.

We only recall the necessary properties and refer the reader to[14,15]for details.Definition 15(Herbrand expansion ofA).LetAbe an infix Skolemized formula(i.e.,A=S(B)for someB).By replacing each occurrence of

where thetiare terms of the Herbrand universe we obtain aHerbrand expansionsofA,denoted byA.

Theorem 1(Herbrands Theorem(original form)).For any formula A there is a Her brand expansion B of A,such that A is valid iff B is valid.

NOTE:It is important to note,thatAisnotuniquely defined,but that there can be different Herbrand expansions for one formula.

Definition 16.Thecomplexityof a Herbrand expansionH,denoted by|H|,is the multiplication of the length of disjunctions and conjunctions created during the ex pansion5See[4]for the definition of the Herbrand complexity..

With HE(A)we denote an Herbrand expansion which is minimal in terms of the complexity.

With HEM(A),whereMis a model ofA,we denote the minimal Herbrand disjunction which is equivalent toAin the modelM.

In the following,when we speak of the Herbrand expansion of a formula,it is supposed that this formula is provable,otherwise there would be no Herbrand expan sion.

The difference between HE(A)and HEM(A)is simply the fact that in certain models ofAthe original Herbrand expansion can collapse because of additional iden tities.

Definition 17.Thesizeof a Herbrand expansion is the number of logical symbols,constants,variables,and function and predicate symbols occurring in it.

Proposition 2.For any Herbrand expansion H of a formula S(A)we can obtain a cut free proof of →S(A)with height exponential in the complexity of S(A).

For any cut free proof of →S(A)we can obtain a Herbrand expansion with complexity exponential in the height of a cut free proof.

4.2 Minimization for Herbrand expansions

We aim at a double exponential bound of the size of Herbrand expansions relative to the complexity of the Herbrand expansion and the size of the original formula.More specificly,for a given formulaA′and a given Herbrand expansionHof the skolemization of the formulaA′we want to find another,possibly different,Herbrand expansion,which has terms with bounded depth and which is,in some sense,minimal.We will explain this concept of minimality later on.

Definition 18.For every occurrence of every syntactic component of a formula(function symbols,variables,predicate symbols,conjunctors,quantifiers) there is a unique signature called thepositionwhich describes the position within the formula.For a positionpcorresponding to a predicate symbol,the operator Atom(A,p)yields the atomic formula for this predicate symbol.

We don’t fix ourselves to a specific way to describe positions in formulas.

Let the given Herbrand expansion be the formulaH:

whereare(lists of)Skolem terms andare(lists of)(regular)terms.

Now we substitute new variables into the formulaHfor thetiand obtainH#:

Note that also the Skolem termsTimay have changed due to the substitution into different termsSi.Since we only changed terms,the positions of atomic formulas withinH#andHare the same.We construct the setMof all pairs of positions,whose corresponding atomic formulas are equal inH,i.e.:

Finally we construct the equality systemGconsisting of all the atomic formulas inH#,which are equal inH:

This equality system has a solution (see [23,24]for the treatment of unification),namely the original substitution which we used to obtain the skeletonH#fromH.

Definition 19(Herbrand Skeleton).The formulaH#obtained fromHby substitut ing new variables for the terms occuring in the formula is calledHerbrand Skeleton.

The mentioned equality systemGdescribes the connections between the atomic formulas withinHwhich renderHtrue,i.e.a substitution,which is a solution of this equality system,will transformH#into a tautology.

For any tautology there can be various ways to exhibit it’s truth.The reasons for being a tautology are the connections between atomic formulas.We are looking for a minimal set of these connections such that the resulting formula is still a tautology.

Definition 20(alternative equality system forH#).A subsetgofGis calledalter native equality systemforH#if there is a solutionσofgwhich transformsH#into a tautology.

Note that all the subsetsghave at least one solution,the projection of the primary solution,but this substitution does not necessarily transformH#into a tautology.

If we have such an alternative equality system it describes a different method of transformingH#into a tautology.

All these alternative equality systems make up a tree where the root is the orig inalGand going down the tree gives smaller and smaller systems.In each branch there is agwhich is the smallest one.From all thesegwe can take one of those,which have the smallest number of equalities,i.e.the smallest number of necessary connections to render the Herbrand disjunction true.

Definition 21(minimal alternative equality system).An alternative equality sys temgis calledminimalif all solutions of all proper subsets ofgdo not transformH#into a tautology.

Of course there can be more than one minimal alternative equality system,de pending on which branch in the above tree we choose.

It is possible to estimate the size of the deepest term in the Herbrand expan sion of a formula:this is just the usual bound coming from the construction of the most general unifier(see[23,24]),namely|t|≤d2|V|,wheredis the maximal term depth before starting the unification and|V|is the number of variables occuring in the termst.

Recall that we use the termdepth,that is the nesting level of terms,and not the term breath(number of symbols).

Lemma 2.The depth of a given term in any minimal Herbrand expansion is boundedby the following formula:

where d is the maximal depth of the Herbrand skeleton of A,k the complexity of the Herbrand expansion and l the number of variable places(or the number of quantified variables)in the Herbrand expansion.

Proof.This is obvious from the construction of the most general unifier.□

Now we have all the ingrediences to prove the following lemma on how to find an Herbrand expansion of a given complexity.

Corollary 1.For any formula A and any integer k it is possible to check(in exptime)whether there is an Herbrand expansion for A with length smaller than k and if there is one it is possible to find it.

For any Herbrand expansion it is possible to find another Herbrand expansion with the same skeleton but with a minimal number of connections within the Herbrand expansion.We will call such an Herbrand expansionminimal.

Proof.For anykstarting from 1 we construct all the terms with depth less than the upper bound given in the above lemma and try all the combinations for substituting these terms into the variables of the expansion and check for a tautology.Since there is only a finite set of terms for anykthe procedure terminates for anyk.□

4.3 Replacement of Skolem terms with constants

The general idea is to take a Herbrand expansionofthe Skolem form,i.e.H(S(A)),and eliminate the Skolem terms which arenotin the original language.We can get rid of these Skolem terms by looking at the reasons out of which an Herbrand expansions is valid:Namely out of purely propositional reasons.If we view the atomic propo sitions,which are syntactically different,as propositional variables,the formula is a propositional tautology.

Using this fact we can transformH(S(A))into a validity equivalent Herbrand expansion ofAby replacing occurrences of terms governed by function symbols which are introduced during the process of creatingS(A) with new constants.By this substitution,the propositional structure of the formula and therefore its validity are retained.

Theorem 3.Any H(S(A))can be transformed into another Herbrand expansion of S(A)where there are no occurrences of Skolem function symbols.

Proof.Following the outline of the proof from above,letf1,…,fnbe all the new function symbols inS(A)andu1,…,uNall the syntactically different terms or sub terms inH(S(A)),which are of the formfi(...)for somei.Without loss of generality assume that the terms are ordered according to the subterm property,with minimal terms first.ConstructSNas follows:

where thecukare new distinct constants.WithinSNthere is no occurrence of any of thefiand it has the same propositional structure asH(S(A)) and is therefore valid,and therefore equivalent toS(A)which in turn is(provably)equivalent toA.ThereforeSNis an Herbrand expansion forA.□

Note that we are indexing the new constants with the Skolem terms.This allows to revert the procedure.

4.4 Deskolemization

According to Proposition 2,we can obtain a cut free proof ofS(A)from a Her brand expansion ofS(A) with exponential expense.From the obtained proof one can eliminate the Skolem terms and reintroduce the original quantifiers,again with exponential expense,see[3].

4.5 Additional properties of Herbrand expansions

In the following we want to estimate the length of a Herbrand expansion from below.This will later be used to prove a non elementary speedup from diagrams to proofs with cuts(Section 6).

The technique used is to reduce the Herbrand expansion to increasingly simple formulas while keeping a bound of the length.We will use some lemmas which are easy to prove:

Lemma 3.If M is a model of A then the Herbrand expansion of A in M is not longer than the(general)Herbrand expansion,i.e.

Lemma 4.The Herbrand expansion of A∧B(in M)is not shorter than the Herbrand expansion of A(in M),i.e.

Lemma 5.If B is not valid in M and is of bounded complexity,then there is an atmost exponential function f such that

Lemma 6.If there is only one witness for(?x)A(x)in a model M and A(t)is valid in M,then the Herbrand expansion of A(t)in M is not longer than the Herbrand expansion of(?x)A(x)in M,i.e.

5 Diagrams Made from Herbrand Expansions

In [22],we gave a definition of a construction and proved the equivalence of diagrams and proofs by translating a given proof in a specific calculus into a proof by constructions.Here we connect diagrams with the more general concept of Herbrand expansions and cut free proofs.

5.1 Operations on constructions

We will define certain operations on constructions,which will be used to trans late Herbrand expansions into diagrams.

Definition 22.The construction of a literalL,denoted byC(L),is generated by constructing the necessary terms followed by the case distinction afterL.Theopen nodeof this construction is the node containing?L.

The following operation will initially create an object which is not a construc tion,because some non terminal nodes are contradictory,and substitutions will not be consistent.But it is always possible(see[21])to transform this into a construction by iterating through all nodes.We will call this operationpruning.

Definition 23.IfC1is a construction with open nodesN1,...,Nn,andC2a con struction with open nodesM1,...,Mn,thenC1⊕C2is the construction obtained by attachingC2onto all open nodes ofC1and prune the tree to obtain a construction.The open nodes ofC1⊕C2are the open nodes of all the copies ofC2.

5.2 Transformation from Herbrand expansion to construction

We want to note that we cannot start with the Herbrand expansion of an arbitrary formula,because we can only prove a formula with a diagram if it is a formula of projective geometry.We therefore assume that a given formulaAwas proven in a sound calculus for projective geometry.

Therefore,the formulaAx ?Ais valid in first order logic and has an Herbrand expansion.The formula we will prove with diagrams will be the expansion ofA,i.e.,the Herbrand expansionAx ?A.

The transformation from a Herbrand expansion to a construction is done in the following steps:

1.Minimizing the term depth

2.Reformation of the geometric part into a DNF

3.Building up the construction from the literals and terms by case distinctions

Part 1 is described in Section 4.5,part 2 is trivial.

For part 3 we use the operations defined above to obtain a construction:

After having added all the literals there should be only closed nodes,some closed by contradictions,some by parts of the Herbrand expansion,but it is not obvious why all the nodes are closed.

Proof.We will prove this theorem by a series of lemmas:

Lemma 7.If there is a construction for a formula A and in another construction there is a node which derives?A,then below this node there are only contradictory leaves.

Proof.Take this node and attach the whole construction derivingA.After pruning of the tree we obtain a construction in which all the nodes are obviously contradictory.

□

Next assume that there is a node in the construction from above which is open,i.e.it is not contradictory and does not derive the Herbrand expansion.Then,for every sub conjunction there must be at least one literal whose negation is in the node.We now need a construction of the Herbrand expansion to close this node.This is not a vicious circle,because we assumed that the original formula was proven.

Lemma 8.If below a node there are only contradictory nodes and no occurrence of a critical constellation,then the node by itself is contradictory.

Proof.LetNbe the upper node,N′(L,R) be the successor(s) andα,(α,β) the actions leading fromNtoN′(L,R).We have to scrutinize all the possible actions on whether they could generate a contradiction in the next node:

Ifα=[PQ]orα=(gh),then the new formulas areP I[PQ]andQ I[PQ],whose negation is not in the upper node because the term isn’t constructed yet.Therefore,if inN′there is a contradiction,it must be already inN.

The argumentation for the other cases are similar.The only situation when this argumentation can not work,is if there is a critical constellation where the following substitutions generate the contradictions.□

Now we have to show how to eliminate rules between certain occurrences of critical constellations.

Lemma 9.If all the leaves under a node N are contradictory,then these contra dictions are automatically derived with the critical constellation procedure,i.e.the procedure which solves only critical constellations until none is left.

Proof.We assume a nodeNwith two successorsLandR,and that the action is a critical constellation(P,Q;g,h),i.e.fromNtoLthere is a vertex labeled withP=Qand fromNtoRthere is a vertex labeled withg=h.Furthermore assume thatLandRare contradictory(otherwise use Lemma 8).

Assume thatNis not contradictory(otherwise we can kill the critical constella tion below and proceed to the next one).Therefore the critical constellation actions generated the contradictions.

We now have to analyze the possibilities how this critical constellation has emerged out of the predecessor ofN.There are four possibilities for actions leading to the nodeN:The joining,the meeting,a case distinction or a critical constellation.The first two are analogous.

First for the joining:It must be the joining ofPandQ,otherwise the predecessor already has a critical constellation.So the critical constellation is in fact(P,Q;[PQ],h).The contradiction inR,where the vertex labeled with[PQ]=his leading to,must be of the form () orhh.In the latter case there must be a for mula[PQ]hinNand therefore also in the predecessor ofN,which is impossible since this term is constructed on the vertex leading toN.

If the contradiction is (),then it can come from either (X I[PQ])or from([PQ])inN.In the latter case the formula[PQ]would be present in the predecessor ofN,too,which is impossible.In the former caseXhas to be eitherPorQ.But ifX=Pthen we would have ()inN,otherwise(),and in both cases already the nodeNwould be contradictory.

The meeting of two lines is handled analogously.

Now for the part where the vertex leading toNcomes from a case distinction.Assume that below the node following the negative vertex there are no other case distinctions(otherwise we start the whole procedure below this).So we can eliminate all the actions below the node and only critical constellations are left.But since the negative literal cannot induce a critical constellation they must already be present in the predecessor ofNand therefore the case distinction can be eliminated.

For the last part,if there is a critical constellation above,we have eliminated all the intermediate actions,as desired to complete the proof.□

We see the importance to know that there is a construction.Because if we start with the procedure from above and end up in an open node,we know that this node is contradictory or the critical constellation procedure produces a subtree with all leaves closed.This is independent of any calculus or deduction rules.

This concludes the proof of Theorem 4.□

One interesting consequence of the way this theorem is proven is that diagrams as they are used are not constructive in the usual sense,meaning that there are non constructive elements in it.One of the most obvious of these elements is the case distinction,which of course is necessary.Another one is the occurrence of critical constellations,which are instances of case distinctions.

This fact,that diagrams aren’t constructive in the strict sense of the word,is inter esting and perhaps surprising,since diagrams are commonly thought of as paradigms of constructive objects.

5.3 An example

We want to give an example for such a diagram:The fact we want to prove is the fact thatA0does not lie on the line through two diagonal points.That is,we want to proof thatA0.For the diagram compare Figure 7.

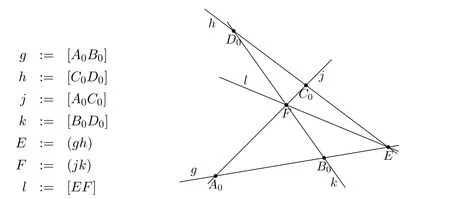
Figure 7:Diagram of A0 l

The corresponding construction tree is given in Figure 8.This example demon strates the automatic deduction of a contradiction with the help of critical constella tions.From node 1 to node 2 the various terms are constructed and renamed,which is a trivial part and no critical constellation will arise.But in node 2 we start prov ingA0by contradiction.We split the construction adding onceA0(node 3r)and onceA0(node 3l).In node 3r a critical constellation arises,which can be solved in two ways,either leading to a contradiction in node 4l or to a new critical constellation in node 4r.The solution to the new critical constellation produces con tradictions in both nodes 5l and 5r,which closes all the nodes below the addition ofA0in node 2.The only open node left over is node 3l,which provesA0.

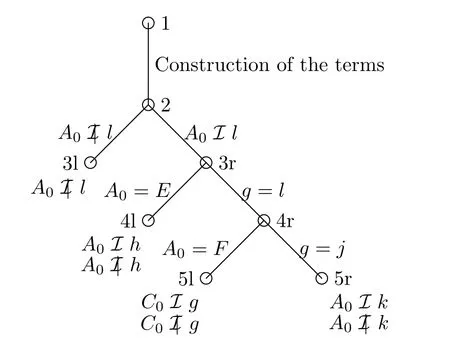
Figure 8:Construction tree for A0 l

5.4 Estimations of the length of the constructions

With the estimate of the length of terms in the Herbrand Expansion given in Section 4.5 we can give an estimate of the length of a construction as follows:

In every step of the construction of the terms and the case distinctions the branches can be split(doubled),which yields the multiplicand of.Furthermore in ev ery final(prefinal)node there can be a chain of critical constellations,but not more than#t,where#tis the number of terms,#lthe number of literals anddmthe maximal term depth.We thus obtain the following (very rough) bound on the lengthlCof a constructionCmade from a HE:

6 Speed up Results between Diagrams as Cut Free Proofs and Proofs with Cuts(Lemmata)

In this section,the fact that we can embed the rational numbers into models of projective geometry,together with an analysis of Herbrand expansions will provide non elementary speedups from diagrams as cut free proofs to proofs with cuts,based on[29]and[18].

To achieve this we will translate Orevkov’s formula into the language of projec tive geometry.Some very old results on the undecidability in the arithmetic of integers and rationals and in the theory of fields by Julia Robinson([25])together with the con cept of representability from G?dels historic work let us define a formula representing the predicatePfrom Orevkovs paper,whereP(a,b,c)holds iffa+2b=c.Finally we will present a detailed analysis of the Herbrand expansion and obtain a lower bound for the cut free proof of the modified Orevkov formula.Together with the short proof from Orevkov’s paper we obtain the mentioned result.We take Orevkov’s series of formulas because it uses no additional function symbols.We will represent recursive functions as presented in[28].

6.1 Orevkov’s speedup formulas

In[18]a series of formulas of first order predicate logic is given for which there is a non elementary speedup in proof depth between cut free proofs and proofs with cuts.Orevkov formalizes the functionf(x)=2xinto a predicatePand iterates this function to get 2i：=fori>0 and 20：=0.

Orevkov denotes bythe formulas

and gives for allka derivation ofwith cut,where the number of sequents depends linearly onk,while on the other hand he proves that in any derivation which is cut free the number of sequents is non elementary ink.

Since we don’t have any free predicate symbols6We are working in a theory!,it is necessary to formulate the same predicate in projective geometry.

The formula we want to construct should have the following properties:There is a short proof in some reasonable calculus,and the Herbrand expansion of this formula is long.

Let us start with a short reminder on projective geometry:In the times when projective geometry was used only for projective closed Euclidean planes over the real numbers,i.e.in our usual geometry,the theorem of Desargues was really athe orem,but with the foundation of projective geometry with axioms it turned out that this theorem is independent of the axioms and therefore projective planes where the theorem is not valid are possible.So today we speak of the Axiom of Desargues.

Definition 25.Two triangles are said to beperspective from a point Oif there is a one to one correspondence between the vertices so that lines joining corresponding vertices all go throughO.Dually,two triangles are said to beperspective from a line oif there is a one to one correspondence between the sides of the triangles such that the points of intersection of corresponding sides all lie ono.

Theorem 5(Axiom of Desargues).If two triangles are perspective from a point,then they are perspective from a line.

The interesting fact with this axiom is that by adding the axiom of Desargues we get as models all the projective planes which can be algebraized,i.e.where there is a field such that the projective plane can be considered as the projective plane over the 3 dimensional vector space over this field.In these planes the field can be defined as one line of the plane and the arithmetic operations of the field can be defined as terms.

This construction is as follows:Take a linegand a distinct lineh,two points 0 and 1 on linehbut not on lineg,a pointRongbut not onhand a linelnot equal tog,hand which passes through(gh)(This is indeed possible!).Then the operations+and?can be expressed in terms of joining and meeting as follows:

It is easy to prove that with this construction the points on linehexcept the point(gh)(which is∞)form a field.Furthermore it is possible to construct an iso morphic projective plane from the 3 dimensional vectorspace of this field.We there fore obtain

Theorem 6.Any Desarguesian projective plane can be algebraized.

Consider the second requirement from above:Since the Herbrand expansion is long if the Herbrand expansion in a certain model is long,it is enough to work in one model.We choose the model of the projective plane over the 3 dimensional vectorspace over the field Q and denote it withPGQ.This model is a Desarguesian plane(see[21])and therefor the operations“+”,“?”,“·”and“/”can be defined as terms as shown above.

Now we have to define natural numbers in this model.This is possible with the following definitions:

LetR(x)state thatxis rational,in our case this is thatxlies on a special line.Then we can define the notion of integer as follows:

which are due to[25],who showed that in the arithmetic of rationals the notion of an integer is definable in terms of addition and multiplication.This proof is based upon results of Hasse concerning quadratic forms([11]).

After having defined the integers we can define positive with the identity of Lagrange,every integer greater than zero is the sum of four squares.Combining the arithmetic operations and the less than relation we can define all the recursive functions(cf.[28]).

Now lets start with Orevkov’s formula and translate it into a form applicable in projective geometry.We think of the predicate letterPno longer as a free predicate,but a formula describing the equalitya+2b=cforP(a,b,c).Furthermore we have to put the axioms in front of the formula,i.e.Ax ?BifBis Orevkov’s formula.And in the formula itself it is necessary to prefix any variable with Nat(v)?···because we want to play only on the natural numbers.The formula Nat(v)stands for the formula we get from Robinson and the translation into projective geometry with the definitions of the arithmetic operations.

6.2 Orevkov’s proof of non elementary speedup and its translation

In this section we will prove the following

Theorem 7.There is a series of formulas which can be proved in linear time using cuts,but only in non elementary time using diagrams.

6.2.1 The long proofs

We will use the following notation:If there is an at most exponential functionfsuch thatxf yforf(x)>y.

So let us start with the analogon to Orevkov’s formula in projective geometry:

We want to estimate the length of the Herbrand expansion of this formula from below.And if we find a non elementary lower bound of the length of the Herbrand expansion we would have proved the one part.We will use the lemmas from above a lot of times to reduce the above formula to the “real” core where a long computation has to be carried out.

According to Lemma 5 we can estimate the length for the above formula by estimating the length of

in the modelPGQ,i.e.there exists an at most exponential functionfsuch that

We will now write out the formulas to see where we have to zoom in to find the core computation:

A partP(a,b,c)is a formula describinga+2b=c,which we obtained from G?del’s representation theorems.Specifically,we can say thatP(a,b,c)looks like(?z)(a+z=c ∧G(b,z))withG(x,y)describingy=2x.Since everyPoccurs in the above formula in the formP(0,x,y),which is(?z)(0+z=y ∧G(x,z)),which in turn is nothing else thanG(x,y),we can writeBk(0)also as

and with the abbreviations

Applying lemmas 4,5 and 6 we have

wherev0=2kandv1=2k?1and so on.This is obvious from the fact that theviare the computed values of 2l,i.e.vi=2k?i.

We have now reduced the analysis from the original formula to the analysis of a simpler formula,the formulaG1≡G(v1,v0)wherev1andv0are number terms.The next step is to look intoG(x,z).Unfortunately here we come to the level where we have to actually use G?del’s representing functions,actually find the representing formula for 2x.

We arrive at the following formulas:

with Seq(),lh(),…are the well known sequence functions.We can writeG(x,z)as

ForG1we obtain

This means thatw1=「(20,21,...,vk)?the G?del number of the respective se quence.According to Lemma 6 we can writeG1as

with the abovew1.So we can estimate the length of the Herbrand expansion again from lemmas 4 and 6

We will now rewrite the formulaw1=(μs)Q(v1,s)with the aim to eliminate all the bounded quantifiers and theμquantifier.

continuing withQ(v1,w1)

If we write

thenL(i,l,w)means thatwis the G?del number of a sequence,which is longer thenlentries,and that there is an indexi

We will now further“simplify”—or better analyze—the last formula from above:

The right disjunct evaluates in the modelPGQto false and therefore the length of the Herbrand expansion of the whole formula can be estimated from below by the length of the Herbrand expansion of the left part.But the left part tells us nothing else than there is no“wrong”index in the sequence determined byw,and therefore this sequence is the sequence of 2i:

Again according to Section 4.5 the length of the Herbrand expansion of the last line can be estimated by the length of the Herbrand expansion of

so we get

Finally we have obtained a formula where we can actually compute a lower bound of the length of the Herbrand expansion,namely the length is greater thanv1,which in turn is 2k?1:

Combining the formulas(2),(4),(5),(6)and(7)we get

wherev1=2k?1andfis an at most exponential function.

We have shown that the Herbrand expansion of the modified formula of Orevkov is longer with respect tofthan 2k?1.It remains to show that there is a short proof in a reasonable calculus likeLPGK.

6.2.2 The short proofs

We now come to the proof that equation 1 can be proved in a few steps,more precisely,we will give a proof of this formula with length linear ink,the index of the formula.

In Orevkov’s paper[18]there is a proof of

In this proofPis a free predicate symbol,while in our context it is a compound formula.The second difference is that there are no“restriction formulas”Nat(x)in his proofs.But these two points do not generate a problem,because

? Orevkov’s proofs can be used if we work in a calculus where compound initial sequents are allowed.This is no problem since the transformation from com pound to atomic initial sequents is linear(see[2]and further improvements).

? Subformulas of Orevkov’s proofs have to be relativized to Nat.

These two changes together with a weakening at the end we get proofs of equation(1)from the original proofs.These proofs have lengths linear ink.

7 Closing Comments

Diagrams lead from special cases to general onesThis analysis presents di agrams as tools to progress from specialized problems to general statements.We described a method to obtain general results from special instances.This is similar to the generalization of Euler’s calculation in[1].

Diagrams are not constructiveAs can be seen from the way diagrams are drawn and the way they are translated to Herbrand expansions it is easy to see that diagrams arenot,as the name suggests,constructive.All this“non constructivity”arises from the concept ofgeneral position,which indeed becomes more difficult to be explained when geometries with higher concepts (distance,angle,…) are introduced.Since Projective Geometry only makes use of the notion of incidence the assumption of a Point in general position is easier to realize than elsewhere in geometry.The concept of general position lacks constructiveness due to atomic case distinctions which have to be made.It is the principle of the excluded middle on atomic level,which makes constructions non constructive.

Theoretical foundations for computer tools for geometric reasoningAs the use and speed of computers increases they are employed more and more as proving tools with the help of programs like Mathematica etc.These programs are already applied to prove theorems and to draw diagrams.This article provides a theoretical framework for such applications.([10,30,33])