Some Fermat-type Indices of Sierpi′nski Graphs and Sierpi′nski Pyramid
GUO Lin(郭林),ZENG Cheng(曾成),GAN Ting(甘庭)
(1.School of Mathematics and Information Science,Shandong Technology and Business University,Yantai 264005,China;2.School of Computer Science,Wuhan University,Wuhan 430072,China)
Abstract: In this study,we present our observations on some Fermat-type indices including Fermat eccentricity,Fermat radius and Fermat diameter.We determine Fermat radius and Fermat diameter of Sierpi′nski graphs and Sierpi′nski pyramid by encoding method.Normalizing distance in Sierpi′nski graphs,we give the precise value of average Fermat eccentricity of Sierpi′nski pyramid and therefore a asymptotic formula of Sierpi′nski graphs is obtained.
Key words: Sierpi′nski graph;Sierpi′nski pyramid;Fermat distance;Fermat eccentricity;Self-similar measure
1.Introduction
LetG=(V(G),E(G)) be a simple and connected graph,whereV(G) denotes the vertex set andE(G)the edge set of the graphG.The Fermat distance functionFonV(G)×V(G)×V(G) is given byF(u,v,w)=minσ∈V(G){d(u,σ)+d(v,σ)+d(w,σ)},that is,the minimum size among all spanning trees ofGcontaining these three vertices.For an arbitrary vertexu ∈G,the Fermat eccentricityε3(u) ofuis defined as the maximum Fermat distance fromuto any other two vertices.Very recently,LI,YU and Klavˇar[1]investigated the Fermat eccentricity of trees and block graphs.The study of Fermat eccentricity provides theoretical support for some problems,such as minimizing maximum time delay and predicting anti-HIV activity[2].
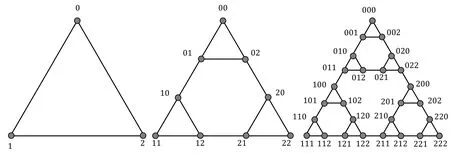
Fig.1 The graphs , , and their labeling
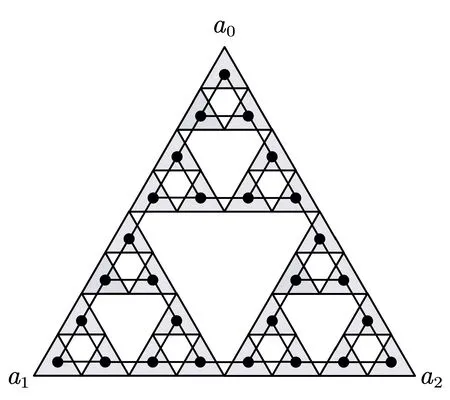
Fig.2 The relation between and
We now give the formal definition of the Sierpi′nski pyramid.Leta0,a1,···,apbe the coordinates of thepcorners of a (p ?1)-dimensional regular pyramidF ∈Rp?1,wherep ≥3.We letTi(x)=x/2 +ai/2 be the contracting similitude fori ∈[p]0.Then the (p ?1)-dimensional Sierpi′nski pyramidis the unique attractor of IFS (Iterated Function System).It is well known that dimH SPp=dimB SPp=logp/log 2.As the cross-research object of fractals and graph theory,the average distance of Sierpi′nski gasketSP3has been discussed in [6]by using the approaches of finite pattern and self-similar measure.However,there are yet no published works on the Fermat-type indices of Sierpi′nski graphs and Sierpi′nski pyramid.Our work is an attempt in this regard.
In our paper,we focus on some Fermat-type indices of Sierpi′nski graphsand their corresponding Sierpi′nski pyramidsSPp,including Fermat eccentricity,Fermat diameter and two types of Fermat radius.
2.Preliminaries
We start with some notations which will be used throughout our paper.
Let|S|be the cardinal number of the setS.Then the order ofGis|V(G)|and the size ofGis|E(G)|.The distancedG(u,v) (d(u,v) for short) between two verticesuandvofGis the length of the geodesic path inGconnectinguandv.The eccentricity of a vertexuinG,denoted byε2(u),is maxv∈V(G)d(u,v).The diameter and the radius of a graph are given byd(G)=maxu∈V(G)ε2(u) andr(G)=minu∈V(G)ε2(u),respectively.It is well known that
Clearly,the Fermat distanceF(u,v,w) is an extension of distance.We call the vertexσthat realizesF(u,v,w) the Fermat vertex.The Fermat eccentricityε3(u;G) (ε3(u) for brevity) ofuisε3(u;G) :=max{F(u,v,w) :v,w ∈V(G)}.The Fermat radius and the Fermat diameter ofGare,respectively,the minimum and the maximum eccentricity,that is,Fr1(G):=min{ε3(u):u ∈V(G)}andFd(G):=max{ε3(u):u ∈V(G)}=max{F(u,v,w):u,v,w ∈V(G)}.We mark(G) as the average Fermat eccentricity ofG.The Fermat co-eccentricityε3,2(u,v;G) (ε3,2(u,v) for brevity) ofuandvinV(G),as the dual of the Fermat eccentricity,is naturally defined asε3,2(u,v;G):=max{F(u,v,w):w ∈V(G)},which deduces the second type of Fermat radius,that is,Fr2(G):=min{ε3(u,v):u,v ∈V(G)}.
where we letQi=Ti(SPp),i ∈[p]0for notational convenience.
3.Fermat Diameter and Fermat Radius
In this section,we present analytical results on Fermat radius and Fermat diameter of Sierpi′nski graphs and Sierpi′nski pyramid by encoding method.We first list a basic lemma that appears in [3].
where the Iverson convention (A)=1,if the statementAis true,and (A)=0,if it is false.Furthermore,
Proposition 3.1For the Sierpi′nski graph
ProofReplace the Fermat vertex of tripletu,v,wbyu,v,win turn,we obtain
and the equality holds ifu,v,ware different extreme vertices.
Lemma 3.2The Fermat distance of vertexuand two extreme vertices insatisfies
Moreover,the Fermat eccentricity of a vertexu ∈is given by
Eq.(3.2) can be easily derived by induction and Lemma 3.1.The second assertion of Lemma 3.2 comes straightforwardly from Eq.(3.2) and the definition ofε3(u).
Lemma 3.2 demonstrates that to determine the Fermat eccentricity of a vertexu,it is sufficient to consider only the Fermat distance ofu ∈to extreme vertices.
Note thatl ≥m.From Lemma 3.1 we of course deduce
Hence we have the following proposition about Fermat radius of.
Proposition 3.2Letp ≥3 andn ∈N+.Two types of Fermat radius are given in turn by
ProofWe elaborate that the proposition holds in the following three cases.
The proposition is therefore proved.
Corollary 3.1For (p ?1)-dimensional Sierpi′nski pyramidSPpandp ≥3,we derive
4.Fermat Eccentricity
Directly from (2.1) and Lemma 3.2,we have the following intuitive lemma.
Lemma 4.1Foru ∈Fk,
ProofFor a given vertexu′=kun?1···u1∈kSn?1p,we have
By the recursive definition of Sierpi′nski graphs and Lemma 3.2,we thus get
Applying (2.1) to (4.1) leads to Lemma 4.1.
We are now prepared for our main result.
Theorem 4.1Forp ≥3,the average Fermat eccentricity ofSPpis given by
Moreover,we have the asymptotic formula for,that is,
wherek ∈[p ?1]0.
By symmetry ofSPp,we have
By Lemma 4.1 and self-similar measure inSPp,Mp?k,pcan be rewritten as
Similarly,the initial valueM2,pis given by
The second assertion of Theorem 4.1 comes straightforwardly from3(SPp) and (2.1).
- 應(yīng)用數(shù)學(xué)的其它文章
- 粘性Cahn-Hilliard方程的二階凸分裂有限元格式
- 求解非線性方程組的修正Fletcher-Reeves共軛梯度法
- Extending Slow Manifold Near an Asymmetric Cusp Point
- The Smoothing Newton Method for NCP with P0-Mapping Based on a New Smoothing Function
- 四耦合非線性薛定諤方程的矢量孤子解及疊加解
- Dynamics of an SVIR Epidemic Model with Markovian Switching

