LIU Xuemei,MENG Jixiang

(School of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830017,China)

Abstract: For a simple non-complete graph G,the h-component connectivity(resp.,h-component edge connectivity)of G is the minimum cardinality of a vertex subset of G whose deletion renders at least h components for any positive integer h.In this survey,we mainly summarize results on h-component connectivity(resp.,h-component edge connectivity)and the exact values of the h-component connectivity(resp.,h-component edge connectivity)of some well-known networks.

Key words: component connectivity;component edge connectivity;Cartesian product;hypercube

0 Introduction and Some Terminology

1 General Results on Component(Edge)Connectivity

Chartrand et al.[3]provided a sufficient condition for a graph withh-component connectivity at leastk,while Oellermann[5]presented a stronger condition than the former,whereh≥2 andk≥0.Recently,the relationship between extra connectivity and component connectivity of graphs has been investigated by Li et al.[6],while the relationship between extra edge connectivity and component edge connectivity of graphs has been suggested by Hao et al.[7]and Guo et al.[8],independently.Moreover,Liu et al.[9]explored the relationship between component diagnosability and component connectivity of a class of regular graphs under some restricted conditions.

1.1 Sufficient conditions for a graph to have h-component connectivity at least k

Chartrand et al.[3]gave a sufficient condition for a graph to haveh-component connectivity at leastkwith respect to minimum degree,while Oellermann[5]obtained a sufficient condition with respect to degree sequence.

Theorem 1(Chartrand et al.[3]) LetGbe a graph of ordern.If δ(G) ≥[n+(h-1)(k-2)]/h」,then(G) ≥kfor 2 ≤h≤α(G).

Theorem 2(Oellermann[5])LetGbe a graph of ordern≥2 with degree sequence(d1,d2,···,dn),whered1≤d2≤···≤dn.Forh≥2 and 1 ≤k≤n-h+1,ifdi≤i+k-2 impliesdn-k+1≥n-i(h-1)for anyiwith 1 ≤i≤(n-k+1)/h」,then(G)≥k.

1.2 Relationship between extra connectivity and component connectivity

Theorem 3(Li et al.[6]) Lethandrbe two nonnegative integers.LetG=(V(G),E(G)) be a graph with |V(G)| ＞(r+1)(h+1)-[h(h+3)/2].IfGsatisfies the following two conditions:

(i)There exists a subgraphAofGwithA?K1,h+1anddG(x)=rfor any vertexx∈V(A),whereV(A)={u,u1,u2,···,uh,uh+1}anduui∈E(G)with 0 ≤h≤r-2 and 1 ≤i≤h+1,such that|NG()∩NG()|=2(1 ≤i1,i2≤h+1 andi1,i2are distinct),|NG()∩NG()∩···∩NG()|=1(1 ≤i1,i2,···,ik≤h+1 andi1,i2,···,ikare pairwise distinct fork≥3)and|NG(u)∩NG(ui)|=0.Moreover,there exists a subgraphA′ofAwithA′?K1,hsuch thatNG(V(A′))is anh-extra cut ofG;

(ii)For any subsetS?V(G)with|S|≤r(h+1)-h(h+3)/2-1,G-Sis either connected or it has a component containing at least|V(G)|-|S|-hvertices,then=r(h+1)-h(h+3)/2.

As applications of the above result,Li et al.[6]explored the extra connectivity or component connectivity for some wellknown networks,including complete cubic networks,hierarchical cubic networks,generalized exchanged hypercubes,dual cube-like networks,Cayley graphs generated by transposition trees and hierarchical hypercubes as well,combined with the known conclusions about the extra connectivity or the component connectivity of them.

1.3 Relationship between component diagnosability and component connectivity

In [9],Liu et al.suggested some characterizations of the (h+1)-component connectivity of a class of regular networks under some restrictions as the following Theorems.Furthermore,they established the relationship between component connectivity and component diagnosability of one class of networks.

Theorem 4(Liu et al.[9]) LetGbe at-regular triangle-free connected network with |V(G)|≥(h+1)(2t-h)+1.IfGsatisfies the following two conditions:

(i)There exists a subgraphAofGwithA?K1,h,whereV(A)={u,u1,u2,···,uh}and(u,ui)∈E(G)with 1 ≤h≤t-2 and 1 ≤i≤h,subject to that|NG(ui)∩NG(uj)|=2(1 ≤i,j≤handi≠j);

(ii) For any subsetS?V(G) with |S|≤th-h(h+1)/2,G-Sis either connected or has a large component of at least|V(G)|-|S|-(h-1)vertices,then=th-h(h+1)/2+1.In fault diagnosis,the PMC model was initially pioneered by Preparata,Metze,and Chien[10].LetG=(V(G),E(G))be a multiprocessor system.Then,for any two distinct faulty setsF1,F2?V(G),under the PMC model,F1andF2is a distinguishable pair if and only if there exists a vertexu∈V(G)(F1∪F2),which is adjacent to a vertexv∈F1△F2,whereF1△F2=(F1∪F2)(F1∩F2).Motivated by the idea of conditional diagnosability,Zhang et al.[11]proposed the(h+1)-component diagnosability of a network recently and they also determined theh-component diagnosability ofn-dimensional hypercubes under both the PMC and MM*models for 2 ≤h≤n+1 andn≥7.For a multiprocessor systemG,

(i)An(h+1)-component fault cutFofGis a vertex set such thatG-Fhas at leasth+1 components;

(ii)A systemGis(h+1)-componentt-diagnosable if and only if for any two distinct(h+1)-component faulty subsetsF1andF2ofV(G)such that|F1|≤t,|F2|≤t,F1andF2are distinguishable;

(iii)The(h+1)-component diagnosability of a multiprocessor system,denoted byis the maximum number of faulty vertices which can guarantee to locate with the condition thatGis(h+1)-component faultt-diagnosable.

Theorem 5(Liu et al.[9])LetGbe at-regular triangle-free network andhbe an integer with 1 ≤h≤t-2.IfGsatisfies the following conditions:

(i)|V(G)|≥(h+1)(2t-h)+1;

(ii)There exists a subgraphAofGwithA?K1,h,whereV(A)={u,u1,u2,···,uh}and(u,ui)∈E(G)with 1 ≤h≤t-2 and 1 ≤i≤h,subject to that|NG(ui)∩NG(uj)|=2(1 ≤i,j≤handi≠j);

(iii)For any subsetS?V(G)with|S|≤t(h+1)-h(h+3)/2,G-Sis either connected or has a large component with at least|V(G)|-|S|-hvertices,then+t-(h+1)=t(h+1)-h(h+3)/2.

As by-products of the above result,Liu et al.[9]presented the (h+1)-component diagnosability of the state-of-the-art compound networks based on hypercube,such as bicube network,generalized exchanged hypercube,hierarchical hypercube,half-hypercube,and so on,combined with the known conclusions about the component connectivity of them.Moreover,Tian et al.[12]explored the relationship between the component diagnosability of hypercubes under the PMC model and its component connectivity.

1.4 Relationship between extra edge connectivity and edge component connectivity

Hao et al.[7]studied the relationship between extra edge connectivity and component edge connectivity of regular graphs as the following two Theorems.Using this relationship,they explored the extra edge connectivity and the component edge connectivity of some well-known graphs,includingBCgraphs,data center networks DCell,augmentedk-aryn-cubes,hierarchical star networks,burnt pancake graphs,(n,k)-star graphs,et al..

Theorem 6(Hao et al.[7]) LetGbe a connected graph and it has an (h+1)-extra edge cut.Let φ be the set of all minimum(h+1)-extra edge cut ofG.Assume thatm=min{|E(G*)|:G*is a component ofG-SforS∈φ},where min is over allS∈φ and all components ofG-S.IfG-Thas at mosth+1 components for anyT?E(G)with|T|≤+m-1,then

Theorem 7(Hao et al.[7]) For a connected graphG,let φ={S?V(G) : |S| ＜|V(G)|/2,bothG[S] andG[V(G)S]are connected subgraphs}andt=minS∈φ{(diào)|E(S,G-S)|}.LetS*∈φ be a subset ofV(G)such that|E(S*,G-S*)|=t,|S*|=sand|E(G[S*])|=m.IfGsatisfies the following conditions:

(i)For any edge cutFofGwith|F|≤t-1,the graphG-Fhas a large component and small components which contain at mosts-1 vertices in total;

(ii)For any edge cutFofGwith|F|≤t+m-1,the graphG-Fhas at mostscomponents,then=t+m=

In[8],Guo et al.investigated the relation between extra edge connectivity and component edge connectivity for regular networks as the following conclusions.

Theorem 8(Guo et al.[8])LetGbe ak-regular super-graph.Then(G)=(G)+1.

Theorem 9(Guo et al.[8])LetGbe ak-regular super-K3-free graph with|V(G)|≥9.Then(G)=(G)+2.

Based on the above results,Guo et al.[8]determined the component edge connectivity ofBCnetworks,k-aryn-cubes and enhanced hypercubes.Also in [8],Guo et al.proposed a conjecture about the relationship between component edge connectivity and extra edge connectivity of regular graphs.

2 Component(Edge)Connectivity of Graphs and Networks

Many researches have been focused on the component(edge)connectivity of some well-known networks in recent years.Little is known abouth-component edge connectivity.In this section,the exact values of theh-component connectivity(resp.,h-component edge connectivity)of several special graphs and some well-known networks are surveyed.

2.1 Several special graphs

The component connectivity of several special graphs,including path,cycle,wheel,complete bipartite graph,complete multipartite graph,tree,has been studied and the results are delivered as follows.

Theorem 12(Li et al.[14])LetTbe a tree with ordern,then 1 ≤(T)≤h-1 for 2 ≤h≤n-1.

Theorem 13(Li et al.[14])LetTbe a tree of ordern≥3.

(a)the maximum degree ofTis at mosth-1,and

(b)there are two verticesuandvsubject todT(u)+dT(v)≥h+2 ifuandvare adjacent ordT(u)+dT(v)≥h+1 ifuandvare nonadjacent.

(a)the maximum degree ofTis 3,and

(b)there are at most two adjacent vertices of maximum degree.

2.2 Cartesian product

LetKn,Cn,Pnbe a complete graph,a cycle,and a path withnvertices,respectively.The independence number of a graphGis represented by α(G).ThekthpowerGkof a graphGis the graph with vertex setV(G)such that two distinct vertices are adjacent inGkif and only if their distance inGis at mostk.The Cartesian productG×Hof graphsGandH:

(i)V(G×H)=V(G)×V(H);

(ii)(x,u)(y,v)is an edge ifx=yanduv∈E(H),orxy∈E(G)andu=v.

Then-fold Cartesian productof graphsG1,G2,···,Gncan be defined recursively as above forn≥2.

2.2.1 Cartesian product of several special graphs

Guo et al.[15]determined the component connectivity of the Cartesian product of some graphs by using Cauchy-Schwarz inequality as follows.

Theorem 14(Guo et al.[15])

2.2.2n-fold Cartesian product ofCk

Lyu et al.[17],Guo et al.[8]and Xu et al.[18]obtained the component connectivity and the component edge connectivity ofQknas follows.

2.2.3n-fold Cartesian product ofKL

Yang et al.[20]determined the component edge connectivity ofas follows.

2.3 Hypercube and some hypercube variants

The exact values ofh-component connectivity(resp.,h-component edge connectivity)of hypercube and several variations of hypercube are recorded in this subsection.

2.3.1n-dimensional hypercubeQn

The hypercube is one of the fundamental interconnection networks.Then-dimensional hypercubeQnis an undirected graphQn=(V,E)with|V|=2nand|E|=n2n-1.Each vertex can be represented by ann-bit binary string.There is an edge between two vertices whenever their binary string representation differs in only one bit position.

2.3.2n-dimensional balanced hypercubeBHn

Then-dimensional balanced hypercubeBHn[23]withn≥1 hasvertices with addresses (a0,a1,···,an-1),whereai∈{0,1,2,3}for 0 ≤i≤n-1.Each vertex(a0,a1,···,an-1)is adjacent to the following 2nvertices:

wherejis an integer with 1 ≤j≤n-1.

2.3.3n-dimensional enhanced hypercubeQn,k

2.3.4n-dimensional dual cubeDn

Then-dimensional dual cube[28],denoted byDn,has 22n-1vertices,each labeled by a(2n-1)-bit binary stringu1u2···u2n-1,andui∈{0,1}fori=1,2,···,2n-1.Two verticesu=u1u2···u2n-1andv=v1v2···v2n-1are adjacent if and only if the following conditions are satisfied:

(i)uandvdiffer in exactly one bit positioni;

(ii)If 1 ≤i≤n-1,thenu2n-1=v2n-1=0;

(iii)Ifn≤i≤2n-2,thenu2n-1=v2n-1=1.

Theorem 24(Zhao et al.[29])Forn≥2 and 1 ≤h≤n-1,=nh-h(h+1)/2+1.

2.3.5n-dimensional shuffle-cubeS Qn

Then-dimensional shuffle-cube[30]withn=4k+2 is denoted byS Qn.Its vertex set is the same as that ofQn.For any vertexu=un-1un-2···u1u0,we definepj(u)=un-1un-2···un-jandsi(u)=ui-1ui-2···u1u0.Then,S Qnis recursively defined as follows.

(i)S Q2isQ2;

2.3.6n-dimensional hierarchical hypercubeHHCn

Then-dimensional hierarchical hypercubeHHCn[32]is defined to be a graph with vertex set{(X,Y)|X=an-1an-2···am,Y=am-1am-2···a0andai∈{0,1}for all 0 ≤i≤n-1},wheren=2m+mandm≥1.Vertex adjacency ofHHCnis defined as follows:(A,B)is adjacent to

(i)(A,Bl)for all 0 ≤l≤m-1,and

(ii)(Am+dec(B),B),where dec(B)is the decimal value ofB.

2.3.7n-dimensional hypercube-like networkGn

The recursive definition of the hypercube-like networks[33]is as follows:

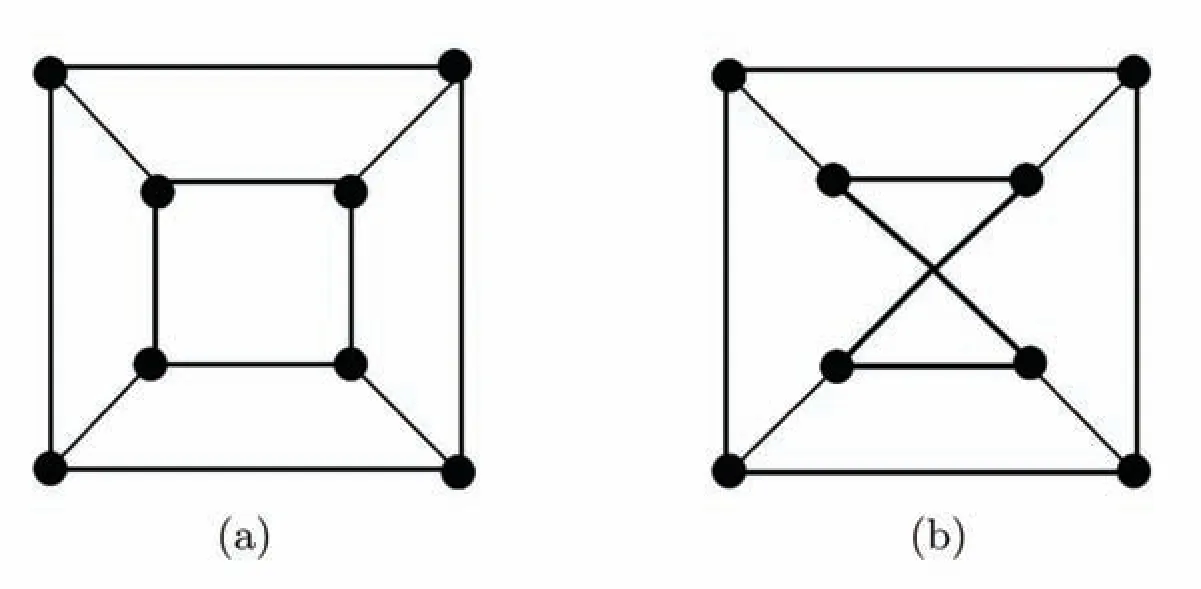
Fig 1 (a)Q3 (b)G(8,4)

Theorem 28(Liu et al.[34])Forn≥8 and 1 ≤h≤2「n,=nh-eh.

2.4 Several well-known networks

2.4.1 Alternating group graphAGn

The alternating group graphAGn[35]can be viewed as the Cayley graph generated by a 2-treeH,where eachK3inHalways contains two fixed vertices.That is,the generating graph ofAGnhas a tree-like(in fact,star-like)structure of triangles.

2.4.2n-dimensional split-star network

Given two positive integersnandkwithn＞k,note that Zn={1,2,···,n},and let Pnbe a set ofn!permutations on Zn.Then-dimensional split-star network[38],denoted bysuch that={(p,q)|p(resp.q)can be obtained fromq(resp.p)by either a 2-exchange or a 3-rotation}.Where

(i)A 2-exchange interchanges the symbols in 1st position and 2nd position;

(ii)A 3-rotation rotates the symbols in three positions labeled by the vertices of a triangle in which three vertices of the triangle are 1,2 andkfor somek∈{3,4,···,n}.

2.4.3m-dimensional DCell network withn-port switchesDm,n

2.4.4n-dimensional burnt pancake graphBPn

2.4.5n-dimensional bubble-sort star graphBSn

Then-dimensional bubble-sort star graph[44],denoted byBSn,is a graph consisting ofn! vertices with each vertex represented by a distinct permutation of[n]and edges described by the transposition graphG(T)with the edge set{(1,i):2 ≤i≤n}∪{(i,i+1):2 ≤i≤n-1}.For(u,v)∈E(BSn),to describe the adjacency ofuandv,we denote byv=u(1,i)for 2 ≤i≤norv=u(i,i+1)for 2 ≤i≤n-1.

Theorem 37(Gu et al.[43])Forn≥3,=4n-9;forn≥4,=6n-16;forn≥4,=8n-24.

3 Conclusions

In addition to the above,there are some results,that are not shown in detail in this survey,about theh-component connectivity (resp.,h-component edge connectivity) of some well-known networks and graphs,e.g.Cayley graph generalized by 2-tree[37],BCnetwork[7,8,45],augmentedk-aryn-cube[7],hierarchical star network[7],(n,k)-star graph[46],folded hypercube[47-50],bicube[51],hierarchical cubic network[52],complete cubic network[53],generalized exchanged hypercube[54-55],generalized hypercube[56],generalized Petersen graph[57],Cayley graph generated by a transposition tree[6,58],star graph[58],godan graph[59],twisted cube[60],locally twisted cube[61-63],divide-and-swap cube[64],crossed cube[65],round matching composition network[66],hierarchical star network[67],bubble-sort network[58,68],augmented cube[69],pancake graph[70],alternating group network[59,71-72],et al..What is more,one may ask a question whether similar results apply to other networks.The exact values ofh-component connectivity(resp.,h-component edge connectivity)are known only for some well-known networks and almost all of them are about smallh.Apart from the aforementioned,the problems of determining theh-component connectivity(resp.,h-component edge connectivity)of many networks for the rest ofhare still open.Several conjectures about the exact value of theh-component connectivity(resp.,h-component edge connectivity)of several well-known networks can be seen in[24,29,37,41].Moreover,extremal aspects of component(edge)connectivity of graphs can be referred to[13-14,73-74],and a conjecture about the size of graphs with given order and component connectivity is presented in[13].