DING Yahao ,Mohammad SHIKH?BAHAEI ,YANG Zhaohui ,HUANG Chongwen ,YUAN Weijie

(1.King’s College London,London WC2R 2LS,U.K.；2.Zhejiang University,Hangzhou 310058,China；3.Southern University of Science and Technology,Shenzhen 518055,China)

Abstract: Although federated learning (FL) has become very popular recently,it is vulnerable to gradient leakage attacks.Recent studies have shown that attackers can reconstruct clients’ private data from shared models or gradients.Many existing works focus on adding privacy protection mechanisms to prevent user privacy leakages,such as differential privacy (DP) and homomorphic encryption.These defenses may cause an increase in computation and communication costs or degrade the performance of FL.Besides,they do not consider the impact of wireless network resources on the FL training process.Herein,we propose weight compression,a defense method to prevent gradient leakage attacks for FL over wireless networks.The gradient compression matrix is determined by the user’s location and channel conditions.We also add Gaussian noise to the compressed gradients to strengthen the defense.This joint learning of wireless resource allocation and weight com‐pression matrix is formulated as an optimization problem with the objective of minimizing the FL loss function.To find the solution,we first analyze the convergence rate of FL and quantify the effect of the weight matrix on FL convergence.Then,we seek the optimal resource block (RB) allocation by exhaustive search or ant colony optimization (ACO) and then use the CVX toolbox to obtain the optimal weight matrix to minimize the optimization function.The simulation results show that the optimized RB can accelerate the convergence of FL.

Keywords: federated learning (FL);data leakage from gradient;resource block (RB) allocation

1 Introduction

Federated learning (FL)[1],an emerging distributed learning algorithm,has received much attention in re‐cent years due to its data protection property[2].This algorithm has been extensively employed in applica‐tions where preserving user privacy is of utmost importance,such as in the case of hospital data[3].FL allows clients to uti‐lize private sensitive data to collaboratively train a machine learning model locally without explicitly sharing individual sensitive data.In the context of wireless networks with lim‐ited bandwidth and latency requirements,the advantages of FL are even more pronounced,especially when there are a large number of users and data.This is because only models or gradients are transmitted,which not only enhances the pri‐vacy of the data but also significantly improves communica‐tion efficiency.

Although FL offers default data privacy by avoiding the ex‐change of raw data between participants and a server,recent studies have noted that FL faces various attacks such as membership inference attacks[4],generative adversarial net‐work attacks[5–6],gradient leakage attacks[7–10],model inven‐tion attacks[11],model poisoning,data poisoning and freeriding attack during the training process[12].These attacks will expose users’ private data,such as the location of confi‐dential sites,and the condition of patients,or corrupt the global model and affect the performance of the model.One of the most advanced privacy leakage techniques is gradient leakage,where an honest-but-curious server could illegally re‐construct the user’s privacy data by performing gradient leak‐age attacks on the client’s uploaded model weights or gradi‐ents.Furthermore,even if the federated server is reliable,gra‐dient leakage can occur by eavesdroppers near the clients or server in the wireless network.Therefore,tackling the gradi‐ent leakage issue is essential for promoting FL in practical ap‐plications,such as edge computing and UAV swarms.

The related work is as follows.

1) Gradient leakage attacks: Gradient leakage attacks are used to reconstruct training input data (e.g.,images or text) and labels through shared gradients or weights.The work in Ref.[7] first discussed the recovery of image data from gradi‐ents in neural networks and demonstrated the feasibility of re‐constructing data from a single neuron or linear layer net‐works.In Ref.[6],a single image was reconstructed from a 4-layer CNN comprising a significantly large fully-connected layer.ZHU et al.in Ref.[8] proposed the deep leakage from gradient (DLG) algorithm.In particular,it yields dummy gradi‐ents by randomly generating dummy data and dummy labels,then minimizing the difference between the dummy gradient and the original gradient,which in turn makes the dummy input close to the original input,and finally recovering the original data.They successfully reconstructed training data and groundtruth labels from a 4-layer CNN.Moreover,they demonstrated that it is indeed possible to recover multiple images from their averaged gradients (maximum batch size of 8).Following up Ref.[8],due to the difficulties of DLG in convergence perfor‐mance and extracting ground truth labels consistently,the im‐proved deep leakage from gradient (iDLG) algorithm was pro‐posed in 2020[9]as a simple and effective method to recover the original data and discover ground truth labels.GEIPING et al.[13]studied the reconstruction of multiple images from their aver‐aged gradients,where they used cosine similarity as a cost func‐tion and optimized the sign of the gradient.The simulations show that it only reconstructs single images from gradients.Fur‐thermore,the work in Ref.[10] introduced a GradInversion method to recover training image batches by inverting averaged gradients.

2) Defense methods for privacy leakage: Recently,a num‐ber of studies have focused on defense strategies for privacy leakage in FL.These methods can be categorized into four types: homomorphic encryption[7,14–15],multi-party computa‐tion[16–17],differential privacy (DP)[18–20],and gradient com‐pression.Homorphic encryption and multi-party computation incur a significant extra computational cost,thus it is not suit‐able for wireless network scenarios with limited communica‐tion resources and delay requirements.For the DP method,it is to add Gaussian noise or Laplacian noise to the gradient be‐fore transmission,which can mitigate privacy leakage,but it also negatively affects the training process and model perfor‐mance[21].Gradient compression defends against data leakage by pruning gradients with small magnitudes to zero so that eavesdroppers cannot match the original gradients.The work in Ref.[8] demonstrated that it is not possible to prevent leak‐age when the sparsity is less than 10%,but when the compres‐sion rate is more than 20%,the recovered image is no longer recognizable,and the leakage is successfully prevented.How‐ever,excessive compression may affect the model's perfor‐mance.Overall,these defense approaches achieve adequate defense either by incurring significant overhead or by compro‐mising the accuracy of the model and they are not specifically designed to defend against data leakage on a gradient[22].Un‐like the general-purpose protection mentioned above,the stud‐ies in Refs.[22–24] focus on defending against gradient leak‐age attacks.SUN et al.in Ref.[22] observed that the classwise data presentations of each client's data are embedded in shared local model updates,which is why privacy can be in‐ferred from the gradient,and the proposed Soteria could effec‐tively protect training data via perturbing data presentation in an FC layer.In PRECODE[23],variational modeling is used to disguise the original latent feature space susceptible to pri‐vacy leakage by DLG attacks.Moreover,WANG et al.[24]pro‐posed a lightweight defense mechanism against data leakage from gradients.They used the sensitivity of gradient changes w.r.t.the input data to quantify the leakage risk and perturb gradients according to leakage risk.In addition,global correla‐tions of gradients are applied to compensate for this perturba‐tion.These three methods provide a significant defense against DLG attacks and have little effect on model perfor‐mance.However,one essential part,wireless network re‐sources (e.g.,bandwidth and power),are not considered in these defense frameworks.

Although the aforementioned methods (Soteria,PRE CODE,and a lightweight defense mechanism) have been suc‐cessful in defending against DLG attacks,all the proposed de‐fense methods focus solely on the theoretical process of FL training and only the server or participants are considered ma‐licious attackers.To the best of our knowledge,there is a lack of research on defending against DLG attacks for FL in wire‐less networks.The fact is that the convergence and perfor‐mance of FL may be affected by bandwidth,noise,delay,power,etc.in dynamic wireless networks.Therefore,to fill in the blank,we propose a novel defensive mechanism,weight compression for gradients,to protect data privacy from DLG attacks in FL.Moreover,we consider external eavesdroppers,such as users around the clients or servers who are not in‐volved in FL training.Key contributions of this work include:

? We propose a novel defensive framework,weight compres‐sion,for protecting the data privacy of FL over wireless net‐works by considering FL and wireless metrics and factors.This defense is implemented by compressing the local gradi‐ent by taking into account the user’s location and channel quality.In addition,Gaussian artificial noise is added to the compressed gradients for further defense.

? We formulate this joint resource allocation and weight compression matrix for FL as an optimization problem with the goal of minimizing the training loss while satisfying the delay and leakage requirement.Thus,our defensive mechanism jointly considers learning and wireless network metrics.

The rest of this paper is organized as follows.The system model and problem formulation are analyzed in Section 2.The analysis of the FL convergence rate is presented in Section 3.In Section 4,the joint optimization problem is simplified and solved.Then,the simulation result and analysis are described in Section 5.Finally,conclusions are summarized in Section 6.

2 System Model and Problem Formulation

In this paper,we consider a small network consisting of one server and a set ofNclients to jointly train an FL model for task inference in a wireless environment,which includes an eavesdropper,as shown in Fig.1.

2.1 Federated Learning Model

In the FL model,the training data as input of the FL algo‐rithm collected by each clientiis denoted asXi=[xi1,…,xiKi],whereKiis the number of samples collected by clientiand each elementxikdenotes theK?th sample of clienti.The matrixyi=[yi1,…,yiKi] is the corresponding labels of training dataXi.After collecting data,each clientitrains its local model using (Xi,yi) and the server aggregates received local models to update the global model for the next round of training.The main objective of the FL training process is to find optimal model parametersw*that minimize the global loss function and the training process can be considered as solving an optimization problem,defined as:

whereK=Kiis the total size of the training data of all clients;wiis a vector that represents the local model of each clienti;f(wi,xik,yik) is the loss function of thei-th client with one data sample.Fi(wi,xi1,yi1,…,xiKi,yiKi) is the total loss function of thei-th client with the whole data sample,which is abbreviated asFi(wi).Moreover,the expression off(·) is application-specific.

In general,Eq.(1) could be solved by performing gradient descent in each client periodically.The detailed training pro‐cess consists of the following three steps:

1) Training initialization: The server first initiates a global modelw0and sets up hyperparameters of training processes,e.g.,the number of epochs and learning rate.The initialized global modelw0is broadcast to clients in the first round.The clients start local model training after receivingw0.

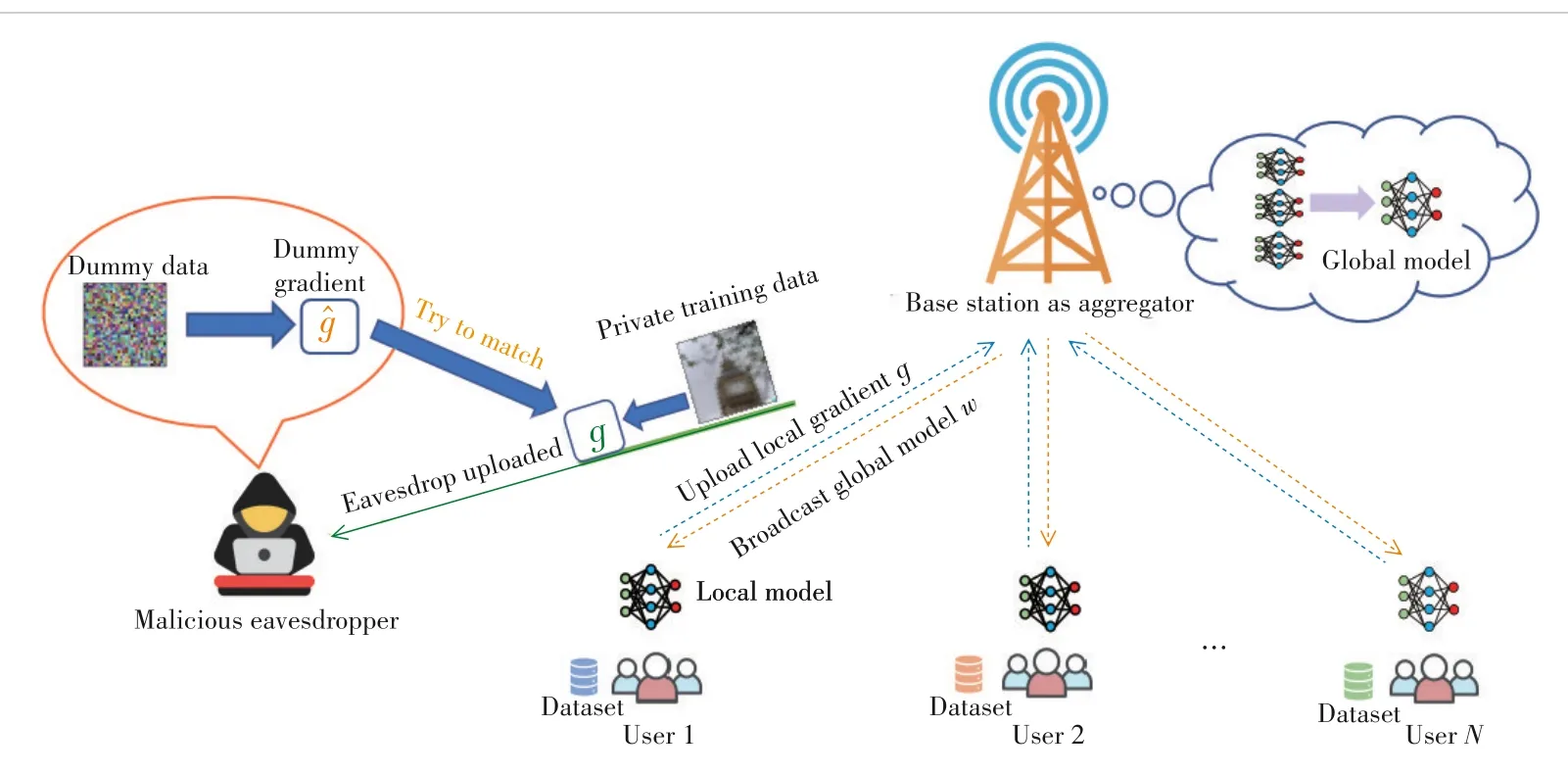
▲Figure 1.Architecture of FL algorithm with one eavesdropper in wireless networks

2) Local training and updating: At each stepj,after receiv‐ing the global weightwjfrom the server,each clientisamples a batch from their own dataset to compute the updated local gradients.

whereis a randomly selected subset ofBtraining data samples from useri’s training datasetKiat thej-th training round.

3) Model aggregation and download: Once the server receives all local gradients fromNclients,it combines them to update the global gradients.Then,the weightswj+1are updated and sent back to the clients for the next training round.The update of the global gradient vector and weights is given by[25]:

whereηis the learning rate.Finally,processes 2 and 3 are it‐erated until the global loss function converges or achieves the desired accuracy.

2.2 Threat Model

In this work,we consider the DLG attack[8]performed by the eavesdropper on the uplink and downlink to recover the original private data from the client.The DLG attack is conducted by making the gap between the generated dummy gradient and the eavesdropped local FL gradient smaller and smaller through multiple iterations,so that the corresponding dummy data be‐come more and more similar to the original data.

We assume that the eavesdropper taps only one nearby cli‐entiat a time,eavesdropping on the last updated local gradi‐ent () of the uplink trans‐mission and the weight (wJ) from the downlink,whereJis the number of iterations for FL to reach conver‐gence.After that,the eaves‐dropper randomly generates a set of dummy inputs=[,…,] and=,…,],which are ini‐tialized as random noise and optimized toward the ground truth datax*.These dummy data and labels are updated by the difference between the dummy gradi‐ent and the original gradi‐ent in each loop.Finally,the privacy data are recovered by minimizing the following objective[10,26].

2.3 Defense Method

Data leakage is mainly caused by the leakage of the gradi‐ent transmitted in the wireless network.Therefore,it can be considered to compress or encrypt the gradient on the client side to make it difficult for eavesdroppers to recover private data.In this section,we propose a defense method against data leakage called weight compression.The weight compression scheme belongs to gradient compression,which is based on the user’s location and channel quality to determine the com‐pression matrix.Local gradients are divided into several parts by the compression matrix and only some of the gradients are sent to the server at a time for aggregation.Moreover,we add Gaussian noise to compressed gradients as the second defense strategy to strengthen the defense.Fig.2 shows the result of ap‐plying DP to defend against DLG attacks.Fig.2(a) illustrates that DLG can recover the original image easily without adding any defense methods and Fig.2(b) demonstrates its effective‐ness with the addition of the Gaussian noise defense approach.

We defineas the weight matrix of clientiat thej?th itera‐tion.To further prevent privacy data leakage,we add artificial Gaussian noise to the compressed gradient,and then the se‐lected partial local gradient is given as:

▲Figure 2.Illustration of the differential privacy (DP) method to pro?tect the privacy of federated learning (FL)

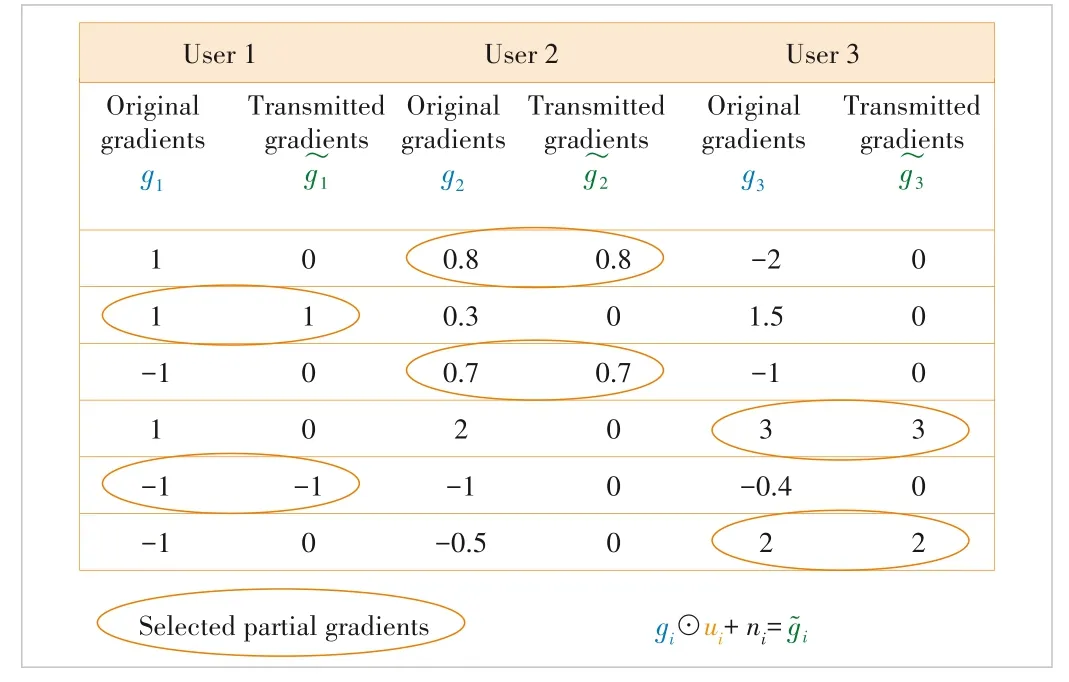
▲Figure 3.An example of proposed weight compression

2.4 Transmission Model

In the FL training process,all clients upload their local FL gradient to the BS via orthogonal frequency domain multiple access (OFDMA).For the uplink,the upper bound of the trans‐mission rate of clientican be given by:

According to the data rate of the uplink in Eq.(10),the transmission delay between clientiand the BS on the uplink can be expressed by:

2.5 Problem Formulation

In order to prevent eavesdroppers from recovering the pri‐vate data of clients and to guarantee FL model convergence,we propose a defense method called weight compression to compress the transmission gradient and formulate an optimiza‐tion problem to implement this joint-designed defense method and the FL algorithm.The objective is to minimize data leak‐age with limited iterations or delays by optimizing the portion selection of the local FL gradient for transmission.The optimi‐zation function is defined by

whereB0is the bandwidth of each RB,Bis the total uplink bandwidth,τis the requirement for uplink transmission delay,andDP0is the constraint of gradient leakage.Eq.(12c) shows the sum of the bandwidth allocated to each user is less than or equal to the total bandwidth of the uplink.Eq.(12e) indicates the compression requirement for the number of valid gradients uploaded by each user.

3 Analysis of FL Convergence Rate

Since we add defense methods to the original FL algorithm,we need to investigate how transmitting compressed gradient affects the performance of FL to solve Eq.(12).Therefore,in this section,we derive the upper bound on the optimality gap of the defense-added FL algorithm.

4 Optimization of Training Loss

In this section,we aim to minimize the training loss of FL by optimizing the weight compression matrix and RB allocation and considering the constraints under the wireless network.We first simplify the objective function in Eq.(12).From Theo‐rem 1and the analysis of FL convergence conditions in Sec‐tion 3,we see that if we want to minimize the training loss of FL,we only need to minimize the gap betweenF(wj+1) andF(w*),under the condition thatA<1.Then we get

Next,we aim to find the optimal RB allocation and weight compression matrix for each user.To accomplish this,we uti‐lize ant colony optimization (ACO) for a large number of RBs and exhaustive search for a small number of RBs.

5 Simulation Results and Analysis

For our simulations,we investigate how the wireless net‐work parameters (Pi,b),user sample sizeKiand gradient com‐pression restrictionsαiaffect the convergence rate under the premise that FL can converge.This simulation topology is a circular wireless network area with a central base station serv‐ingN=5 uniformly distributed users withd=30 m.Specifi‐cally,we consider only six RBs and five users,first finding all solutions forbby exhaustive search (at most one user is as‐signed two RBs),and then we solve the optimization problem by using a CVX (a Matlab‐based modeling system for convex optimization) toolbox and MOSEK solver in MATLAB.Other key parameters used in this simulation are listed in Table 1.

Fig.4 shows how the change ofPiand the allocation of RBchange the objective function value,i.e.,the convergence rate of the FL algorithm.As can be seen from Fig.4,with the in‐crease ofPi,the objective function first decreases and then tends to remain unchanged.This is because when the user power increases,the uplink transmission rate of the user be‐comes larger,allowing the user to upload more gradients,thus accelerating the convergence speed and optimizing the objec‐tive function.However,whenPiis very large,the optimal num‐ber of gradients that users can upload is already saturated due toDP0constraints,so the objective function cannot continue to decline.

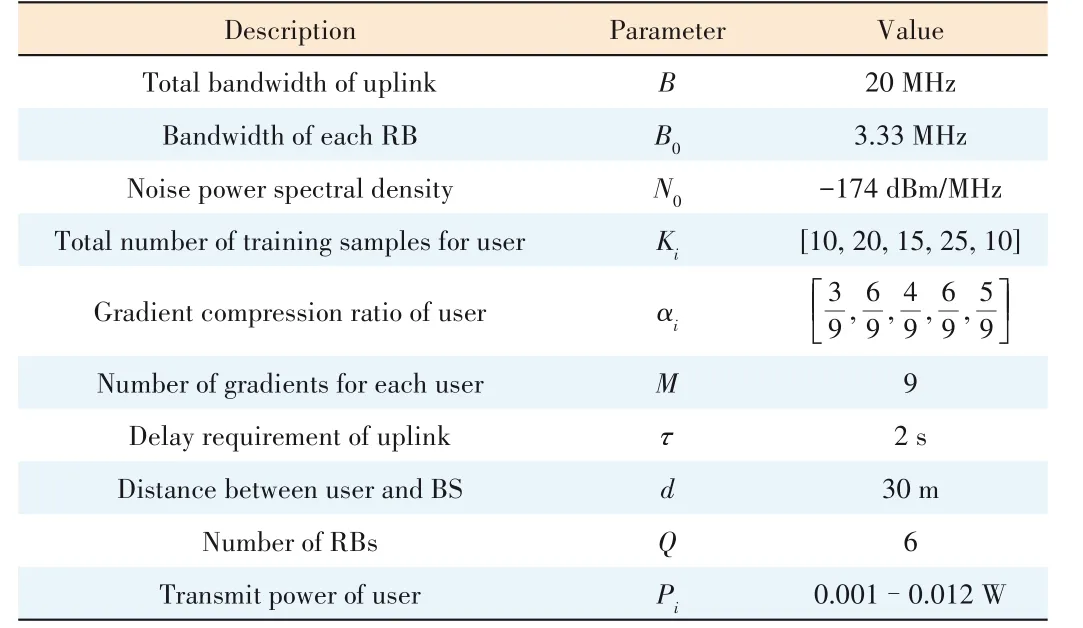
▼Table 1.Simulation Parameters

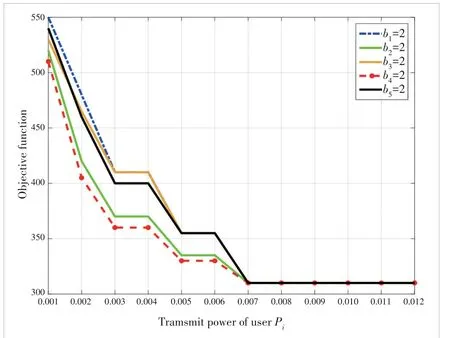
▲Figure 4.Objective function as user power and resource block (RB) al?location varies

Different RB allocations also affect the convergence speed of FL at the samePi,and here we analyze three cases.The ob‐jective function value of the red line in Fig.4 is the smallest,which is because the number of samplesK4and the compres‐sion ratioα4of user 4 are the largest.Therefore,assigning more RBs to the user with more samples and largerαican in‐crease the transmission rate of that user and reduce the total delay of uplink transmission,thereby accelerating the conver‐gence speed.WhenKiis the same butαiis different,that is,the blue line and the black line,the largerαiis,the smaller the value of the objective function is.The reason is that ifαiis large,more gradients can be transmitted,so assigning more RBs to it will result in faster convergence.Whenαiis the same andKiis different,i.e.,green and red lines,the largerKiis,the smaller the value of the objective function is.This is because the largerKiis,the smallerDP0is and the smallerρi,mis.According to Constraint (30e),moreui,mcan be taken as 1,resulting in a smaller objective function and better performance.Overall,optimizingbcan make the con‐vergence faster given a fixedPi.

6 Conclusions

In this work,we propose a novel defensive framework to pro‐tect data privacy from DLG attacks in wireless networks.We jointly optimize RBs allocations and weight compression ma‐trix to minimize FL training loss.We first formulate this opti‐mization problem and simplify it by finding the relationship between the weight matrix and FL convergence rate.Optimal RB allocation is solved by ACO for a large number of RBs and exhaustive search for a small number of RBs.The optimal weight matrix is solved by the CVX toolbox.The simulation re‐sults illustrate that optimizing RBs can effectively improve the convergence speed given fixed user power.