XU Xinyi,LIU Shengli,YU Guanding

(Zhejiang University,Hangzhou 310027,China)

Abstract: As a popular distributed machine learning framework,wireless federated edge learning (FEEL) can keep original data local,while uploading model training updates to protect privacy and prevent data silos.However,since wireless channels are usually unreliable,there is no guarantee that the model updates uploaded by local devices are correct,thus greatly degrading the performance of the wireless FEEL.Con‐ventional retransmission schemes designed for wireless systems generally aim to maximize the system throughput or minimize the packet error rate,which is not suitable for the FEEL system.A novel retransmission scheme is proposed for the FEEL system to make a tradeoff between model training accuracy and retransmission latency.In the proposed scheme,a retransmission device selection criterion is first designed based on the channel condition,the number of local data,and the importance of model updates.In addition,we design the air interface signal‐ing under this retransmission scheme to facilitate the implementation of the proposed scheme in practical scenarios.Finally,the effectiveness of the proposed retransmission scheme is validated through simulation experiments.

Keywords: federated edge learning;retransmission;unreliable communication;convergence rate;retransmission latency

1 Introduction

With the construction of smart cities,a large num‐ber of Internet of Things devices,smartphones and other mobile devices have emerged from all aspects of our lives.The current society has en‐tered the era of big data,and hundreds of millions of data are generated on mobile terminals every day[1–3],which poses novel challenges to both traditional centralized machine learning approaches and wireless communication tech‐niques[4–5].On the one hand,due to a large number of data,uploading all data to the cloud would result in a huge commu‐nication burden[6],and on the other hand,since the data con‐tain user privacy,such as medical health and personal prefer‐ences,uploading raw data to the cloud would bring about the problem of privacy leakage[7–8].

To overcome the abovementioned challenges,a distributed machine learning framework named federated edge learning (FEEL) has been proposed recently[9–11].Under FEEL,mul‐tiple distributed mobile devices use their locally dispersed data to jointly train a common machine learning model,rather than transferring raw data to a central node.The original data containing user privacy are stored on mobile devices,and only the intermediate data,such as gradients and parameters,are transmitted so that user privacy can be protected.In addition,FEEL shifts the model training process from the center to the local devices,thus making full use of distributed computing resources.Due to the advantages brought by the special archi‐tecture of FEEL,it has been intensively used in the fields of healthcare,computer vision,finance,etc.[12–15]

Recently,most research on FEEL assumes that communica‐tion links are reliable.For example,Ref.[16] considers the method of minimizing the transmitted energy under the delay constraint to improve the performance of FFEL.However,in practice,especially in wireless FEEL,channel transmission is generally unreliable due to random channel fading,shadow‐ing,and noise.The accuracy of the intermediate data transmis‐sion during training cannot be guaranteed[17].Retransmission is an important means to improve the accuracy of transmission in wireless communication systems,but with the cost of in‐creasing the communication delay[18].However,with the appli‐cation of FEEL in medical and autonomous driving,it is more sensitive to the accuracy and delay of transmission[19].This motivates us to investigate novel retransmission schemes for FEEL in this paper.

1.1 Related Work

There have been several studies considering the channel unreliability of wireless communications in distributed learn‐ing systems.In Ref.[20],the wireless channel in the FEEL system is modeled as an erasure channel and a scheme for this situation is proposed,which inherits the previous round of gradient when the packet is lost.Based on this,the au‐thors further analyze the influence of coding rate on wireless FEEL in Ref.[21].In Ref.[22],a decentralized stochastic gradient descent method under the user datagram protocol (UDP) is proposed to reduce the impact of unreliable chan‐nels on decentralized federated learning.Moreover,an asyn‐chronous decentralized stochastic gradient descent algorithm is proposed in Ref.[23] to reduce the impact of unreliable channels by performing asynchronous learning and reusing outdated gradients in device-to-device (D2D) networks.The authors in Ref.[24] have proposed an unbiased statistical re‐weighted aggregation scheme from the perspective of gradi‐ent aggregation,which comprehensively considers node fair‐ness,unreliable parameter transmission,and resource con‐straints.In Ref.[25],a sparse federated learning framework is proposed,which compensates for the bias caused by unre‐liable communication through the similarity between local models,and adds local sparseness to reduce communication cost,which further improves performance.In Ref.[26],a fed‐erated learning framework is proposed,where the central server aggregates the global model according to the received parameters and the transmission correct probability,thereby reducing the impact of unreliable transmission.The authors in Ref.[27] further propose a decentralized D2D framework under unreliable channels,which reduces the impact of unre‐liable channels by jointly optimizing the transmission rate and bandwidth distribution.

From the perspective of wireless communication,retrans‐mission has been applied to many current communication standards,including 5G and WiFi.So far,only a few works have studied the retransmission issue in distributed learning.Retransmission can improve the reliability of data packets,but it also reduces the timeliness of data.In some scenarios,it may even be considered to improve the timeliness of data at the cost of reduced reliability[28].In Ref.[29],a Hybrid Auto‐matic Repeat reQuest (HARQ) protocol suitable for multilayer cellular networks has been proposed,which can enhance error detection and correction in D2D communications.In Ref.[30],a retransmission scheme based on data importance is proposed for the edge learning system.The specific ap‐proach of this scheme is to make a tradeoff between the signalto-noise ratio (SNR) and the uncertainty of the data,and corre‐spondingly establish a threshold for retransmission.

1.2 Motivations and Contributions

As aforementioned,in wireless FEEL,devices upload gradi‐ents to the edge server through wireless channels,which is un‐reliable.This will affect the performance of model training.The goal of conventional retransmission schemes is to maxi‐mize the throughput of correctly transmitted data.However,the performance of FEEL with unreliable channels is limited by traditional retransmission since FEEL has different goals of learning accuracy and learning latency.In particular,the im‐portance of data from different devices is different and gener‐ally contributes differently to the model training process.In addition,the communication cost introduced by retransmis‐sion of each device is also different due to various channel fad‐ing environments.The above factors need to be considered when developing a retransmission scheme for the edge learn‐ing system.The main contributions of this paper can be sum‐marized as follows.

? We first propose a FEEL framework with unreliable chan‐nels,in which the gradients uploaded by the local devices are split into multiple packets,and the wireless channel exists the packet error rate (PER).Unreliable transmission leads to bias between the actual global gradient and the theoretical one,which is detrimental to model training.

? We mathematically analyze the effect of PER on the con‐vergence rate and communication cost.To mitigate the impact of unreliable communications on learning performance,the re‐transmission device selection is optimized by making a trad‐eoff between convergence rate and communication cost.

? We derive the optimal solution to device retransmission selection,which greatly improves the model training perfor‐mance.We also analyze the performance of the proposed re‐transmission selection scheme and develop a signaling proto‐col for retransmission.

? We employ a convolutional neural network (CNN) model of the CIFAR-10 and MNIST datasets to test the learning per‐formance of our proposed retransmission selection scheme.Test results show that our proposed scheme outperforms sev‐eral existing retransmission schemes.

The rest of the paper is organized as follows.In Section 2,we introduce the system model.In Section 3,the principle of retransmission design is introduced,and the corresponding protocol is proposed.In Section 4,we analyze the retransmis‐sion gain and cost and formulate the retransmission selection optimization problem.The retransmission selection is derived in Section 5.Finally,we draw the conclusions in Section 6.

2 System Model

2.1 Machine Learning Model

As depicted in Fig.1,we consider a FEEL system consist‐ing of one edge server andKdevices.Devicekhasnklocally labeled data,and the total number of data in the entire system can be represented as.All devices only use their own data to jointly train a machine learning modelwwith the edge server,and the specific method is stochastic gradient de‐scent (SGD).Considering the imbalance of data distribution,the global loss function can be written as:

whereLk(w) is the loss function of devicek,and we have

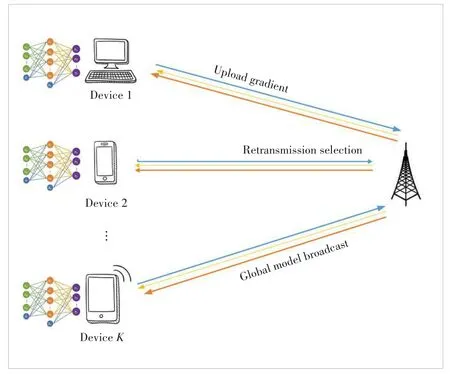
▲Figure 1.Federated edge learning system

wherexi,krepresents thei-th training data of devicek,yi,krep‐resents the corresponding label,andf(?) represents the loss function of the training model.Some popular machine learning loss functions are summarized in Table 1.

The purpose of federated training is to find the optimalw*that minimizesL(w).FEEL is different from the traditional centralized machine learning framework.In the FEEL frame‐work,all the original data are kept on local devices,and the training results are uploaded to the edge server.In thet-th round of training,the selected devices use the local data and the global modelwtreceived from the edge server to obtain the loss functionLk(wt),and upload the gradient ofLk(wt) to the edge server,which can be written as:

After receiving the uploaded gradients of all selected de‐vices,the edge server decodes the data packets and aggre‐gates the global gradientgtas:

▼Table 1.Loss function for popular machine learning models

Then the edge server uses the global gradientgtobtained by the aggregation to update the model,that is,wt+1=wt-ηgt,whereηis the learning ratio.After completing the update of the global model,the edge server broadcasts it to each device in the system.In this way,one round of iterative training of FEEL is completed.

2.2 Wireless Communication Model

In this paper,we utilize time division multiple access (TDMA) as the multiple access method.In a TDMA scenario,all devices use the same frequency band in different time slots and upload gradients to the edge server in turn.During one training iteration,it is assumed that the expected channel state information can be obtained by the channel estimation al‐gorithms.Among the training iterations,the channel of the it‐eration differs from one another.The expected channel state information in each iteration is separately adopted for the per‐formance analysis.Therefore,when a device uploads the gradi‐ents,it will occupy the full bandwidth,denoted byB.For ease of analysis,it is assumed that the wireless channel is static at each training gradient upload and changes in different rounds of training iterations.It is further assumed that the distances of all local devices to the edge server are known,and the small-scale fading is modeled as Rayleigh fading.Then,we can express the uploaded data rate of the devicekas:

whereis the transmit power of devicek,is the channel power gain between the device and the edge server,andN0is the noise power over the whole bandwidthB.We assume that each device is uploading and retransmitting data at the maxi‐mum available power.Note that this assumption fits many sce‐narios,such as LTE[31].

Since wireless channels are generally unreliable,channel er‐rors need to be considered.It is assumed that the uploaded gra‐dients of each device are divided into several packets,and each packet has redundant encoding for error detection.In this pa‐per,the cyclic redundancy check (CRC) code is used to check for errors.Then the PER of devicekcan be expressed as:

wheremis the PER decision threshold[32].

Since the global model sent by the edge server to all de‐vices is the same,the downlink channel can be modeled as a broadcast channel and a more robust encoding method can be used.In this paper,we consider that the channel error occurs only in the uplink channel,and assume that there is no chan‐nel error in the downlink channel.Let the channel bandwidth of the downlink channel beBD,and denoteγas the smallest SNR among all devices,and then the achievable downlink data rate is expressed as:

3 Retransmission Protocol

In this section,we first introduce the principle of retrans‐mission design in FEEL.Then,we propose a novel retransmis‐sion protocol and develop the corresponding processing mod‐ules for both devices and the edge server.

3.1 Principle of Retransmission Design

In FEEL,the edge server performs global model updates by periodically aggregating local gradients uploaded by devices.Therefore,the performance of the trained model depends on the quality of the gradients received by the edge server.How‐ever,unreliable gradient transmission may occur due to wire‐less channel impairments including interference,noise and shadowing.Therefore,it is predicted that the performance of model training is largely affected by channel impairments.

A common solution to unreliable transmission is retransmis‐sion.Conventionally,the purpose of retransmission is to ensure the reliability of data and at the same time maximize the system throughput.However,the main goal of FEEL is to maximize the training accuracy for a given training time.Therefore,a novel retransmission protocol is required for the FEEL system.

When designing the retransmission protocol for a FEEL sys‐tem,one should consider both the training accuracy and the ad‐ditional communication cost brought by retransmission.Re‐transmission can reduce erroneous packets so that the gradient updates received by the edge server deviate less from the ground-truth gradient,which can improve the convergence speed and the accuracy of model training.However,retransmission also increases the communication latency,resulting in an in‐crease in training time.Therefore,we need to properly select the devices that need to be re‐transmitted and design appropriate signaling to make a fair tradeoff between learning accuracy and learning latency.

3.2 Retransmission Protocol and Processing Module

In our proposed retransmission protocol,not all devices participate in retransmission,that is,retransmission selection is required.Consid‐ering the characteristics of FEEL,the device se‐lection depends on not only the channel condi‐tions but also the local data volume and the im‐portance of the upload gradient.Gradient up‐dates that have a more significant impact on global model training will be retransmitted with a larger probability.Moreover,the latency caused by retransmission should also be accounted for.In our proposed protocol,a device with a higher data rate is also more likely to be retransmitted because it brings less addi‐tional communication cost.In addition,the PER between the device and the edge server shall also be taken into account.Due to the robustness of model training,devices with a small PER would bring little performance gain when retransmitting.Also,for a device with a large PER,the reduction of the PER after retransmission is very limited,but it will cause a rela‐tively large communication cost.Therefore,when the PER is too large or too small,the probability of the device being se‐lected for retransmission is both small.

We also consider a new design of retransmission signaling,as shown in Fig.2.Under the traditional retransmission scheme,after receiving an erroneous packet,the edge server only sends a negative acknowledgement (NACK) signal to the device,requiring the device to retransmit.Until the edge server successfully decodes the data packet,it sends an ac‐knowledgement (ACK) signal to the device,and the device starts to transmit the next data packet.In our protocol,when an edge server receives a packet and detects an error using CRC codes,it sends a signal to the corresponding device that includes the information shown in Fig.2.

In Fig.2,NACK indicates that the packet is transmitted with an error,but unlike that in the traditional retransmission schemes,it does not indicate that the device needs to retrans‐mit the packet.Whether to retransmit needs to be judged ac‐cording to the retransmission selection algorithm.Retransmis‐sion allowed signalνkindicates whether the device is selected for retransmission,which is related to the channel conditions,the number of local data,and the importance of the gradient.Specifically,νk=1 indicates that the devicekis selected for re‐transmission;otherwiseνk=0 indicates no retransmission.Whenνk=1,it is equivalent to traditional NACK.Error packet index represents the gradient position contained in the transmis‐sion data packet.If it is selected for retransmission,the device can retransmit the gradient of the corresponding position.

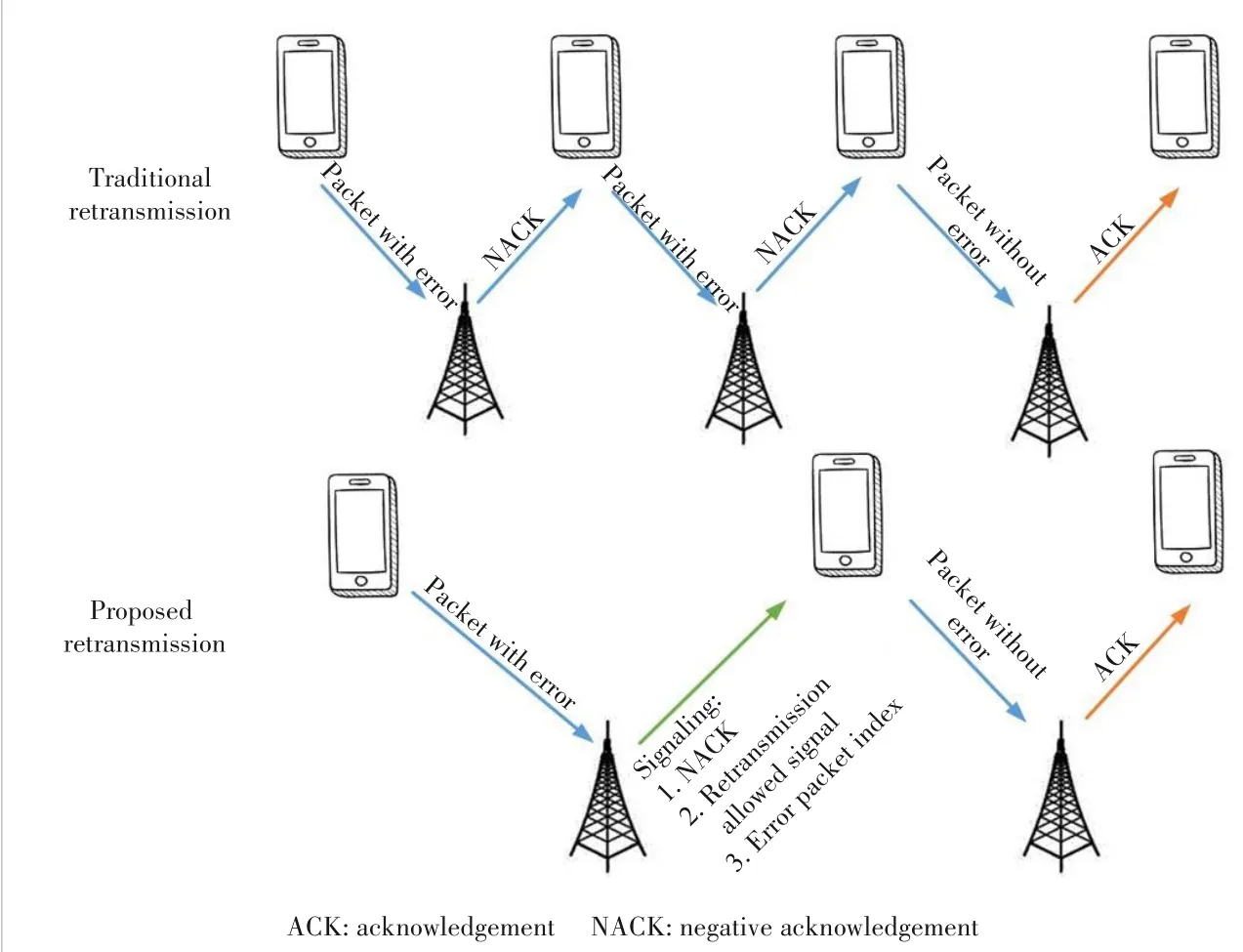
▲Figure 2.Retransmission signaling

According to the received signal,the device will determine whether the uploaded packet is transmitted correctly and whether it is allowed to retransmit.After that,it retransmits the particular data corresponding to the erroneous packet,as indicated by the edge server.

4 Retransmission Design

In this section,we first analyze the one-round convergence rate with unreliable channels.Then,we propose a new crite‐rion to evaluate the gain of retransmission on learning perfor‐mance.The retransmission cost is analyzed as well.Based on this,we formulate a mathematical optimization problem to make a tradeoff between retransmission gain and retransmis‐sion cost.

4.1 One-Round Convergence

Due to the PER,during one round of training,the global gradient obtained by the edge server using the received gradi‐ent is not equal to the theoretical gradientgtin Eq.(4).There‐fore,we define the actual global gradient obtained by the ag‐gregation under the unreliable channel asgt,and we have:

Based on the above assumption,we can obtain the conver‐gence rate of one round under an unreliable channel.

Theorem 1: When the learning rate,the training loss function in one round can be written as:

See Appendix A for details.

From Eq.(12),it can be seen that the loss function is con‐strained by three terms.The first term E{L(wt)} represents the loss function of the previous training round,which is inde‐pendent of unreliable transmissions.The second itemis related to the theoretical gradient value of this round,which depends on the data in local devices,but is inde‐pendent of PER and the retransmission scheme.The third termis the bias term introduced by channel er‐rors,which will reduce the loss function,thus affecting the convergence speed.In order to reduce the influence of unreli‐able channels and improve training performance,we need to reduce channel interference.Therefore,we next analyze the impact of PER () on the gradient bias.Since we focus on the retransmission design of each round,for the con‐venience of presentation,we ignore the superscripttthat rep‐resents the number of training rounds in the following.

We first assume that the machine learning model has a total ofDlayers of neural networks,and the device divides the cor‐responding gradients intoDpackets during the uploading pro‐cess.Thed-th packet contains gradient updates for thed-th layer of the neural network,which is denoted asgk,d.Let indi‐catorρk,ddenote whether the transmission of thed-th packet of devicekis correct.That is,ρk,d=1 indicates that there is no error in the transmission,which means that the edge server can decode and obtain the correct gradientgk,d,and there is a probability ofP(ρk,d=1)=1-pk.Similarly,we letρk,d=0 denote the occurrence of a transmission error with probability ofP(ρk,d=0)=pk.After the edge server receives the pack‐ets,if the error is detected and retransmission is not consid‐ered,the corresponding gradient is set to zero,which can be written as:

Lemma 1: The impact of error transmission on learning per‐formance can be expressed as the bias of gradients caused by packet transmission errors,which can be written as:

First,the gradient bias term is affected by the PERpk.The larger the PER of the device is,the larger the error term will be,and the smaller the loss function will decrease in one round.Second,the error term is affected by the number of lo‐cal data on each device.The larger the number is,the more significant the impact of the device’s PER on the entire model.Third,the error term is also affected by the gradient ob‐tained from training.The larger the sum of uploaded gradients is,the larger the bias term would be introduced.Finally,since the global gradient is obtained by aggregating the uploaded gradients of selected devices,the bias term can be expressed as the sum of the bias introduced by each device due to unreli‐able transmission.Through the above analysis,we can obtain the convergence rate of one round in the presence of transmis‐sion errors as:

4.2 Gain of Retransmission

Next,we analyze the learning performance gain brought by retransmission.Define the PER of devicekafter the retrans‐mission selection asqk,which can be written as:

wherepkis the probability that an error occurs in one transmis‐sion,andνk(1-pk) represents the probability that devicekis selected for retransmission and there is no error in the retrans‐mission.Based on Eq.(14),considering the retransmission,the impact of PER on the convergence can be expressed as:

whereorrepresents the bias between the theoretical gradients and the actual gradients after retransmission.

The PER of the device selected for retransmission will be reduced after retransmission,and its impact on learning per‐formance will also be reduced.Therefore,we can present the following definition to analyze the gain which is achieved by retransmission.

Definition 1: We define the gain of retransmission as the difference between the bias of global gradients before and af‐ter retransmission on the learning performance,which can be written as

Eq.(19) reveals that the retransmission gain of the device is related to the number of local data,the value of the gradi‐ent update,and the reduction of the PER before and after re‐transmission.A larger data volume and gradient value of the device will bring a larger gain of retransmission to the learn‐ing performance.This solution can also be applied to dy‐namic wireless channels,just changing the retransmission PER to the actual PER.

4.3 Cost of Retransmission

Although device retransmission will bring gains to the learn‐ing performance,retransmission will also increase communica‐tion latency due to the additional resource required by retrans‐mission.Therefore,we give the definition of the cost of retrans‐mission as follows.

Definition 2: The cost of retransmission of devicekis de‐fined as the increase in latency introduced by retransmission,which can be expressed as

whereqis the number of quantization bits andNis the total number of parameters.

4.4 Problem Formulation

Until now we have analyzed the gain and cost of retransmis‐sion.Retransmission will bring a gain in learning performance but increase additional communication costs.Therefore,we need to consider the tradeoff between cost and gain when de‐veloping a retransmission scheme.Our goal is to maximize re‐transmission gain while minimizing retransmission cost.We defineβ∈[0,1] as a factor for the tradeoff between retrans‐mission gain and retransmission cost,and the following re‐transmission gain-cost tradeoff problem can be established.

Eq.(21a) represents the retransmission indicator limitation.Whenβis close to 0,it means that the main goal is to reduce the latency when retransmission is selected.Whenβis close to 1,it means that improving the convergence rate is the main goal.

5 Retransmission Optimization and Theoreti?cal Analysis

In this section,we first give a retransmission selection strat‐egy based on P1.Then,we analyze the effect of PER on re‐transmission selection.

5.1 Optimal Solution

By inserting Eqs.(16),(19),and (2) into Eq.(21),and relax‐ing the {0,1} variableνkto [0,1],P1 can be formulated as:

Eq.(22) consists of two parts: the first part is related to feder‐ated learning (FL) training loss,and the second part is related to FL one-round training latency.This is a classical convex op‐timization problem,and the optimal solution can be obtained through the Karush-Kuhn-Tucker (KKT) condition.

Theorem 2: The retransmission selection policy can be ex‐pressed as:

Theorem 2 reveals that the retransmission indicator is a value bounded by 0 and 1,which is related to the local data vol‐ume,gradient value,data rate,and the PER of the device.Spe‐cifically,the probability of being selected for retransmissionincreases with the data numbernkand the gradient valuein the order of.This is because with a large number of device data and gradient values,the learning performance gain ob‐tained by retransmission is also large.Also,increases with the data rateRkin the order of-1.Since the data rate is large,the communication cost of retransmission will be small,and the probability of the device being selected for retransmission will increase.The impact of the device PER on the retransmission selection will be analyzed in the next section.

Since the obtainedis the optimal solution after relax‐ation,we need to consider how to convert it into a {0,1} vari‐able for retransmission selection.We give two strategies.The first is to perform threshold processing on,with 0.5 as the limit.If≥0.5,it means retransmission,and if<0.5,it will not be retransmitted.The second is to sort all devices from large to small according to the value of,and select the largest proportionM% of devices offor retransmission.The choice ofMreflects the tradeoff between model accuracy and training latency.

5.2 Theoretical Analysis

In this section,we will analyze the impact of PER on the re‐transmission indicator.We first define:

From Eq.(24),mkis related to the number of local data,gra‐dient value and data rate,but is irrelevant to the PER.When the local data volume,the gradient value,and the uploaded data rate of devicekare large,devicekis more important in the retransmission design,andmkis correspondingly small.Therefore,mkreflects the contribution of the gradient of de‐vicekto the global model training,as well as the state of its channel.Andmkis always greater than 0.Moreover,the im‐portance of device decreases asmkincreases.Then,in order to analyze the influence ofpkon the retransmission indicator,we define the following function:

wheref(pk) is a strictly unimodal function withpk∈[0,1].See Appendix D for details.

Theorem 2 reveals that the optimal retransmission indicator first increases and then decreases withpk.Therefore,there ex‐ists an optimalthat maximizesf(pk).This result is rather intuitive,which shows that there is a tradeoff between retrans‐mission gain and cost.For the device with a low PER,due to the robustness of neural networks,retransmission has little gain in learning performance,but will increase communica‐tion cost.Therefore,its probability of being selected for re‐transmission is relatively low.For the device with a relatively high PER,there will still be a high PER after retransmission.Thus,the gain in model training performance is not large.Also,the retransmission cost is large,and the probability of being selected is low.Note that devices with intermediate PER can improve the accuracy of gradient data after retrans‐mission,and will not bring reused data or additional deviation.

6 Numerical Result

In this section,we conduct extensive experiments to verify the effectiveness of the proposed retransmission scheme.

6.1 Simulation Settings

Assume that the coverage area of the edge server is 1.5 km,and there areK(K=10) mobile devices that are randomly dis‐tributed across the cellular network.The transmit power of each device is 28 dBm,and the transmit power of the edge server is 33 dBm.Then,the noise power spectral density is-174 dBm∕Hz and the PER decision thresholdm=0.2 dB.Since in the TDMA scenario,all devices occupy one channel to upload gradients.The uplink channel takes into account large-scale fading,given by 128.1+37.6log(d),wheredrep‐resents the distance between the device and the edge server in kilometers.We also consider small-scale fading of the channel,specifically represented by Rayleigh fading.All de‐vices and the edge server jointly train a CNN model.We choose CIFAR-10 and MNIST as datasets.CIFAR-10 con‐sists of 50 000 training images and 10 000 testing images.And MNIST consists of 55 000 training images and 5 000 testing images.The datasets are both non-identically and in‐dependently distributed (non-IID) and divided into 10 cat‐egories.Also,we choose the learning ratioη=0.05.We quantize each element of the uploaded gradient with 16 bits.All elements of each layer are treated as one packet,and a 32-bit CRC code is added.Other major parameters are listed in Table 2.

6.2 Performance of Proposed Retransmission Scheme

Based on the previous theoretical analysis,the proposed al‐gorithm can make a tradeoff between reducing the gradient ag‐gregation bias caused by unreliable transmission and control‐ling the transmission delay,thereby accelerating the model convergence.We use the global training loss and global test accuracy to evaluate the learning performance of the whole learning system.In the simulation of this section,the discreti‐zation method for the retransmission factoris to take 0.5 as the threshold.That is,the selection indicator is set to 0 ifis less than 0.5 and set to 1 if it is larger than 0.5.

The comparison algorithms in Fig.3 are shown as follows.

? Without PER: The wireless channel is ideal and PERfree,meaning that all gradients can be transmit‐ted correctly.

? Without retransmission: There is PER in the uplink channel,but retransmission is not considered.If the uploaded data packet is judged to be incorrect,it will be set to zero and the packet will be discarded.

? Existing retransmission schemes: Using the existing retransmission scheme based on the transmission result.The devices retransmit the er‐roneous data packets after receiving the NACK.

? The proposed retransmission scheme: Us‐ing the scheme proposed in this paper,we made the retransmission selection according to the de‐vice’s local data,gradient data,and PER.

We first perform simulations under the CIFAR-10 dataset.The curves of training loss and test accuracy versus training time under different retransmission schemes are shown in Fig.3.As can be seen from the figure,when transmitting on a reliable channel,no retransmission is required.At this time,the model training can reach convergence in a very short time with a high model accuracy.When the channels are unreliable and retransmission is not performed,the per‐formance of model training will be greatly degraded.When retransmission is not performed,model training can reach convergence very fast,but the accuracy of the final model is pretty low.As a result,when there is no retransmission,the communication cost is relatively small.Although multiple rounds of training are required,one round of training latency is short,so the overall latency is short.However,due to the large bias between the received gradient and the local gradi‐ent,the performance of the final trained model is not satisfac‐tory,which also confirms the necessity of retransmission.It can also be seen that,in the existing retransmission scheme,although the accuracy of the final model is high,it takes much longer time to converge.This is because the existing re‐transmission scheme aims to maximize the throughput,without considering selecting retransmission devices,or the importance of uploading gradients for model training.Due to a large num‐ber of transmitted gradient data and participating training de‐vices,the wireless FEEL system needs to spend a lot of time to achieve model convergence with‐out retransmission selection.Therefore,the exist‐ing retransmission schemes cannot exhibit good performance under the FEEL system.As shown in Fig.3,the retransmission scheme proposed in this paper can make the model training converge in a short time,and achieve high accuracy at the same time.The reason is that the influence of different gradients has been considered in the re‐transmission.This scheme can maximize the re‐transmission gain,reduce the influence of chan‐nel errors,and improve the performance of model training by selecting proper retransmis‐sion devices.In order to further illustrate the ef‐fectiveness of our proposed scheme,we increase the number of devices to 20 for simulation,and the results are shown in Fig.4.

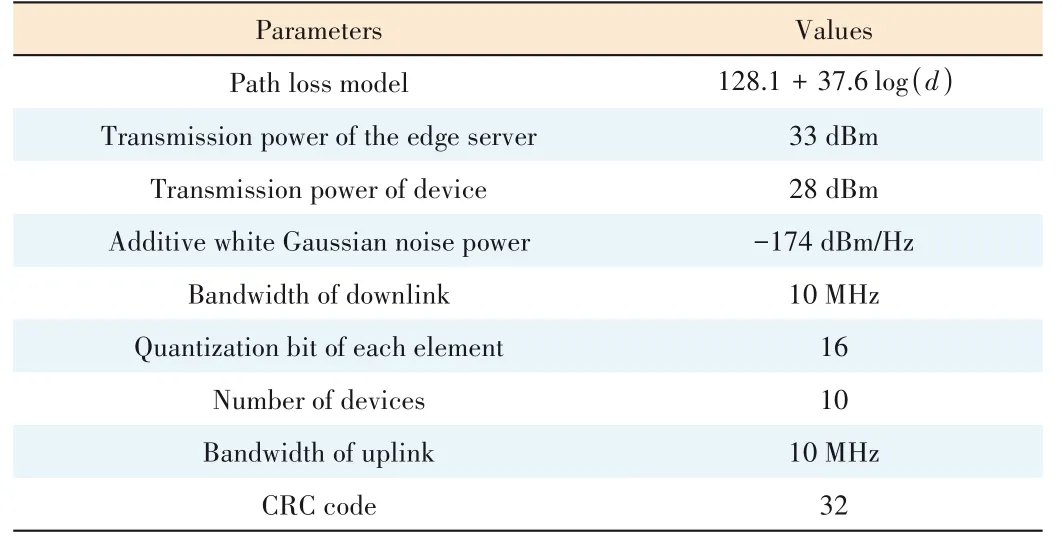
▼Table 2.Simulation parameters

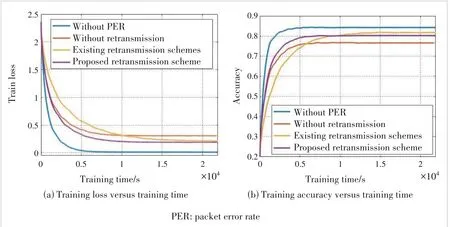
▲Figure 3.Performance comparison between transmission schemes under CIFAR-10

6.3 Performance with Difference Retrans?mission Ratios

When selectingM% of devices for retrans‐mission in each round of transmission,the choice of parameterMmay reflect the tradeoff between model accuracy and training latency in our proposed retransmission scheme.

From Fig.4,whenMis too small,e.g.,20% or 40%,both the convergence rate and final model accuracy become low.This is because the im‐pact of channel error is strong when the number of selected retransmission devices is small.WhenMis too big,e.g.,80%,the convergence speed is low and the final accuracy has no sig‐nificant advantage.This is because retransmis‐sion will increase the latency,and some devices are not of high importance,resulting in limited retransmission gain.

6.4 Performance Comparison Under Other Datasets

To verify the broad effectiveness of our pro‐posed scheme,we change the training dataset to MNIST for further simulations.MNIST con‐sists of 0–9 numbers handwritten by different people.The curves of training loss and test ac‐curacy are shown in Fig.6.After the dataset is changed,the effect of channel unreliability on model training and the performance improve‐ment of our proposed scheme can still be seen.From Fig.7,the proportionMof retransmission devices still affects performance,which further proves the necessity of retransmission device selection.

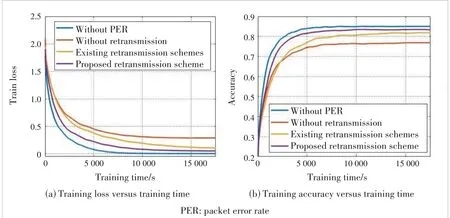
▲Figure 4.Performance comparison between different retransmission schemes under CIFAR-10 with device number K=20

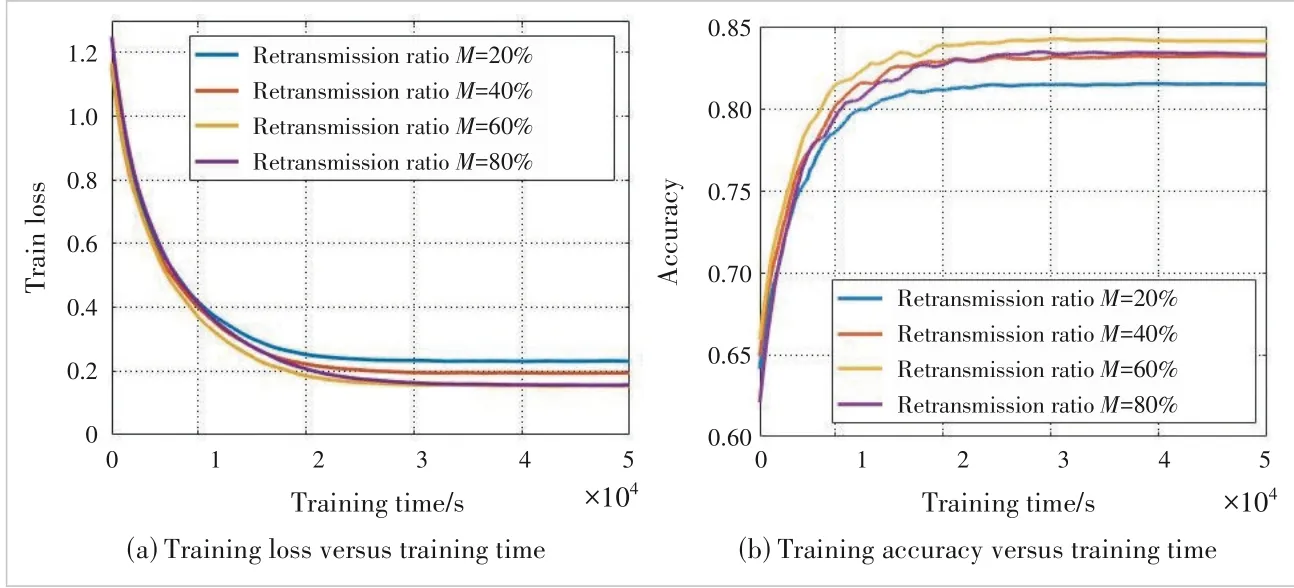
▲Figure 5.Performance comparison between different M under CIFAR-10

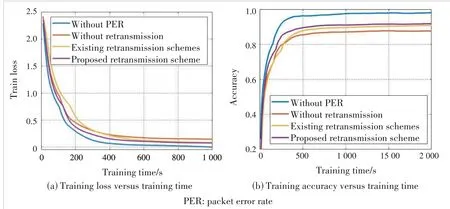
▲Figure 6.Performance comparison between transmission schemes under MNIST

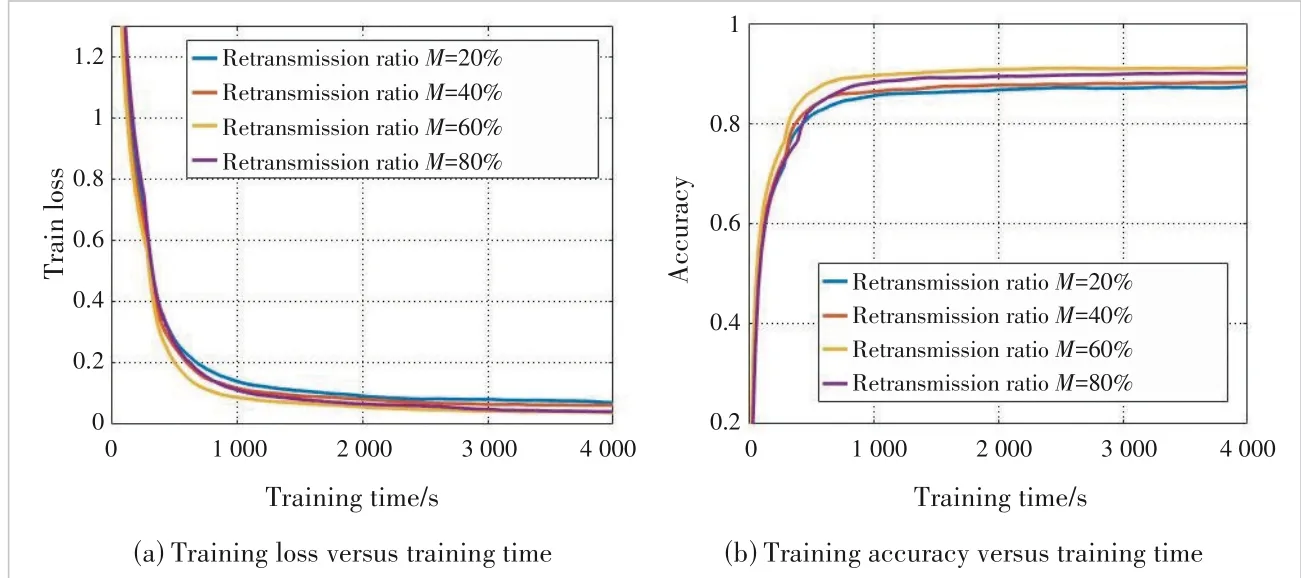
▲Figure 7.Performance comparison between different M under MNIST

7 Conclusions

In this paper,we mainly study the retransmission design for FEEL under unreliable channels.We first analyze the impact of unreliable transmission on the training performance of the FEEL model,and derive the relation between the loss function and the channel PER in one round.Based on this,we analyze the gain to the convergence rate brought by device retransmis‐sion,as well as the communication cost introduced.Then,we propose a retransmission selection scheme for FEEL with un‐reliable channels,which can make a tradeoff between the training accuracy and the transmission latency.It comprehen‐sively considers the channel conditions,the number of local data,and the importance of updates.We also present the air interface signaling and retransmission protocol design under the proposed retransmission selection scheme.Finally,the ef‐fectiveness of the proposed retransmission scheme is verified by extensive simulation experiments.The results show that our proposal can effectively reduce the impact of unreliable wireless channels on the training of the FEEL model,and is superior to the existing retransmission schemes.

Appendix A

Proof of Theorem 1

We first use the second-order Taylor expansion ofL(wt+1) to get

Thus,we have completed the proof of Theorem 1.

Appendix B

Proof of Lemma 1

First,the bias term can be expressed as the difference be‐tween the ground-truth gradient and the aggregated gradient,which can be expressed as

Appendix C

Proof of Theorem 2

First,we take the first-order and second-order differentials of the objective function,and get

So the objective function of P2 is convex.In addition,Eq.(22a) is a linear constraint.Therefore,we can conclude that P2 is convex and we can use the KKT condition to find the optimal solution.We define the Lagrangian function L un‐der the inequality constraints,as

By solving the above equations,we can get the optimal solu‐tion,as shown in Theorem 2.

Appendix D

Proof of Theorem 3

Taking the partial derivative off(pk) overpk,it follows

whereis related tomk.And sincemk>0,∈(0,1).

Therefore,we can prove thatf(pk) increases on (0,) and decreases on (,1).