Jie Li(李杰) Wen-Hui Guan(管文慧) Shuo Yuan(袁爍) Ya-Nan Zhao(趙亞男)Yu-Ping Sun(孫玉萍) and Ji-Cai Liu(劉紀(jì)彩)

1Department of Mathematics and Physics,North China Electric Power University,Beijing 102206,China

2School of Physics and Optoelectronic Engineering,Shandong University of Technology,Zibo 255049,China

Keywords: pulsed Laguerre-Gaussian laser beams, high-order radial mode, optical power limiting, reverse saturable absorption

1.Introduction

Since the invention of lasers,the strong field laser has attracted considerable research interest due to its great brightness, strong directionality, excellent monochromaticity and good coherence as a result of its high photon degeneracy.To broaden the application range of a laser, the pursuit of shortwidth or high-power lasers has always been a hot topic in the research field of laser technology.[1]Laser techniques produce huge advantages for human society, whereas they also pose a potential hazard for human eyes and optical sensors.[2]Therefore, laser protection and related studies are also active topics in the research areas of nonlinear optics and material sciences.[3-9]

The propagation of light in a nonlinear optical medium is affected by both nonlinear refraction and nonlinear absorption processes.[10,11]Nonlinear optical processes for realization of the optical power limiting (OPL) effect[12,13]involve nonlinear scattering,[14]photorefraction,[15]self-focusing, selfdefocusing, two-photon absorption (TPA),[16-20]reverse saturable absorption(RSA)[21-26]and so on.Among them,RSA has attracted considerable attention from experimentalists and theorists and has been widely studied.Generally,in a nonlinear optical medium with RSA characteristics,weak linear absorption of the ground state mainly occurs when the incident light intensity is low, whereas strong excited-state absorption takes a crucial role with the increase in the light intensity and intensively decreases the transmittance of the light field,leading to the OPL effect.

The ability to generate and shape optical beams with novel spatial-temporal structures has increased dramatically in state-of-the-art laser technology.[27-29]Laguerre-Gaussian(LG)laser beams,[30-32]as a class of optical field with cylindrical symmetry,have been well produced due to their promising applications in laser manufacturing,micromechanical manipulation, quantum optics, optical communication and so on.[33-40]Compared with the fundamental transverse mode Gaussian beam, the higher-order LG beams are beams with transverse spatial modes and may even carry photonic orbital angular momentum.Such beams have attractive applications in many fields, such as optical information capacity expansion, optical super-resolution imaging, optical tweezers, and optical fabrication.For example, the high-order spatial LG33mode has been proposed to be used in the laser interferometer gravitational wave observatory to reduce the coupling of the thermal noise to the gravitational wave readout.[33]Singleringed LG beams with doughnut-like transversal intensity distributions and orbital angular momentum about their axis were used to extend the capabilities of laser tweezers for lasing trapping and micro-manipulation.[34-37]With the enhancement of laser power, the nonlinear optical effects of the high-order LG beams gradually appear in their applications.Although the strong field nonlinear optical and propagation effects of the fundamental Gaussian beams have been extensively studied, related investigations with the high-order LG beams are still rare.For example, the propagation behavior of the light bullets in LG and Bessel optical lattices with spatially modulated linear and nonlinear refractive indices were investigated,and showed that the shape of the light bullets and the width of the stability domain can be controlled by the nonlinearity modulation depth.[38,39]The optical limiting properties of an LG beam with the first-order azimuthal index using the selflensing effect was demonstrated experimentally in a thin dyedoped polymer sample.It was shown that the peak phase shift in the sample required for limiting is smaller than that for a fundamental Gaussian beam, and that the nonlinear medium can be placed either in front of or behind the beam focus with higher flexibility.[40]

The LG modes form a complete set of solutions to the paraxial wave equation, and are indexed by two mode numbers,called the azimuthal and radial indexes,respectively.The azimuthal index indicating the orbital angular momentum of the beam has been extensively studied and widely used, but very little research has been conducted on the radial mode number until recently, which was referred to as the “forgotten quantum number”.[41,42]Due to the special multi-ring light field distribution of the high-order radial mode LG beam, it has potential applications in two-dimensional optical lattices,optical manipulation, optical processing, and pulse shaping.Therefore,growing interest has been paid to the radial modes of LG beams due to their unique characteristics of light field distribution.[43-46]

In this paper, we investigate the strong nonlinear optical interaction between pulsed LG laser beams of high-order radial modes with zero orbital angular momentum and the fullerene C60molecular medium;[47-49]special attention is paid to the OPL behavior of the laser pulses during propagation.C60is chosen here due to its good nonlinear optical properties, such as wide absorption spectra, rather fast intersystem crossing rate, long triplet state lifetime, low ground state absorption and strong triplet state absorption, which result in the strong reverse saturable absorption ability of the medium.In our study, we solve the mutually coupled paraxial wave equation and the rate equations within a five-level model.The Crank-Nicholson and the predictor-corrector numerical schemes are used to simulate the evolution of the light field and the population transfer in the molecular medium.It is found that the initial pulsed LG beam is strongly reshaped during its propagation in the C60molecular medium,and clear OPL behavior is observed for different orders of the LG beams before the takeover of the saturation effect.Although the energy transmittance of the high-order radial mode LG beam is higher than the fundamental Gaussian beam of the same initial peak intensity, it has a higher damage intensity threshold and its OPL behavior breaks down later under a relatively higher input field intensity.

The paper is organized as follows.We start in Section 2 with the theory and the physical model of the interaction between the pulsed LG laser beam and the fullerene C60molecular medium.Subsection 2.1 gives the paraxial wave equation presented in the local time frame, and Subsection 2.2 shows the rate equations simplified according to the decay time hierarchy of the molecular system using the adiabatic approximation method.The properties of the pulsed LG laser beams and the molecular parameters are presented in Subsection 2.3.The results of simulations and discussions are presented in Section 3.Subsection 3.1 mainly shows the nonlinear dynamics of population transfer induced by the nanosecond LG laser beams,and the pulse shaping and optical power limiting processes are illustrated and discussed in Subsections 3.2 and 3.3.Our findings are summarized in Section 4.

2.Theoretical models

Generally, in the semiclassical theory of the interaction between light and matter, the light field is regarded as a classical electromagnetic field, and its evolution is described by Maxwell equations, while the properties of the molecular medium are considered quantum mechanically.In this paper,we study the nonlinear optical dynamics of the nanosecond pulsed Laguerre-Gaussian laser beams in the fullerene C60molecular medium.Taking into account the time hierarchy of the studied system,here we applied the paraxial wave equation theory and reduced rate equations to describe the propagation of the laser beam and the strong nonlinear optical interactions in the molecular medium.

2.1.Paraxial wave equation

The propagation of the electromagnetic field in an optical medium is traditionally described by Maxwell equations.Assuming that the electromagnetic field propagates mainly in thezdirection in a non-magnetic optical medium without free charge and free current,by using the slowly varying envelope approximation, one can obtain the following paraxial wave equation:

whereε0is the vacuum conductivity,n0is the linear refractive index of the solvent, andcis the speed of light in vacuum.Here,E(r,t) andP(r,t) are, respectively, the slowly varying envelope distribution of the electric field?(r,t) =(1/2)E(r,t)exp[i(k·r-ωt)]+c.c.and the macroscopic polarizationP(r,t) =P(r,t)exp[i(k·r-ωt)]+c.c.as functions of the position vectorrand the timet.The relationship between the wave vectorkand optical-field angular frequencyωisk=n0ω/c.Meanwhile, Δ⊥is the twodimensional Laplace operator in the plane perpendicular to the propagation direction.

If we separate macroscopic polarization into the imaginary part representing the light absorption and the real part representing the light refraction,the paraxial wave Eq.(1)can be expressed as

whereσtot=[2kIm(P/E)]/(Nε0)is the total absorption cross section of the medium,δn= [n0Re(P/E)]/ε0is the nonlinear refractive index depending on the light field intensity,Im(P/E) and Re(P/E) represent the imaginary and real parts ofP/E, andNis the concentration number of the molecule.

The first derivative terms with respect to timetand positionzexist simultaneously in Eq.(2).To reduce the derivative terms in Eq.(2),here we introduce the retarded time transformationt＇=t-n0z/cto obtain the paraxial wave equation in the local time frame,which can be written as

Apparently, the time derivative term of paraxial wave Eq.(3)disappears in the local time frame,but the electric field and the polarization vectors are still functions of the retarded timet＇.The transformation of the local time frame not only simplifies the form of the wave equation, but also reduces the computational work in the numerical simulations.One can also see from Eq.(3)that by neglecting the weak influence of the nonlinear refractive indexδn, the propagation of the field in the local time frame does not depend on the linear refractive indexn0of the solvent.

2.2.Rate equations

In the optical band,one can describe the reverse saturable absorption of the fullerene C60molecule under the excitation of a light field using a five-level model that includes three singlet states|S0〉,|S1〉,|Sn〉and two triplet states|T1〉,|T2〉.[21,47]A diagram of the five-level system is depicted in Fig.1.

Since the relaxation rate of the non-diagonal elements of the density matrix is much higher than that of the diagonal elements,the change in the population distribution can be ignored during the relaxation time of the off-diagonal elements.Therefore, the rate equations describing the evolution of the population in the five-level system (Fig.1) can be written in the following form:

whereρS0,ρS1,ρSn,ρT1,ρT2are,respectively,the populations of the states|S0〉,|S1〉,|Sn〉,|T1〉,|T2〉, andΓS1,ΓSn,ΓT1,ΓT2are the decay rates of the states|S1〉,|Sn〉,|T1〉,|T2〉.Here,Γcis the rate of intersystem crossing from the singlet|S1〉state to the triplet|T0〉state, andγS1S0,γSnS1,γT2T1represent the fieldinduced rates of one-photon transition|S0〉 →|S1〉,|S1〉 →|Sn〉,|T1〉→|T2〉,respectively.The one-photon transition rateγij(t)between two adjacent energy levels|i〉and|j〉under the action of a light field with frequencyωand intensityI(t)can be expressed by the corresponding absorption cross sectionσijas

Furthermore, since the excited states of the system also have fast relaxation times with picosecond orders of magnitude,while the effective time of population transfer between the singlet state and the triplet state as well as the duration of the incident pulse has the order of nanosecond,it would be reasonable to also use adiabatic assumption with the populationsρS1,ρSnandρT2in the related excited states.More explicitly,one can see from Eq.(4)and Fig.1 that when the duration of the pulseτand the effective time of population transferτST(t)fromρS0toρT1are much longer than（ΓS1+γc+γS1S0(t)+γSnS1(t)）-1,(ΓSn+γSnS1(t))-1, (ΓT2+γT2T1(t))-1, which are, respectively,the characteristic transfer times ofρS1,ρSn, andρT2, the time derivatives terms ofρS1,ρSn, andρT2in Eq.(4) can be neglected.Such an adiabatic condition of the populations is easier to meet with faster decay rates of these excited states, for example, by increasing the population number density of the molecules.Therefore, the five partial differential rate equations for the five-level system can be reduced to one partial differential equation explicitly about the evolution of the population in the ground state,

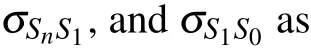
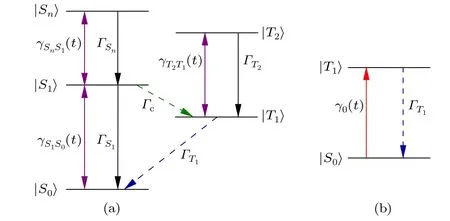
Fig.1.A diagram of the traditional five-level model of the fullerene C60 molecule (a), and the effective rate of population transfer γ0(t) in the simplified two-level model based on the adiabatic approximation(b).

2.3.Pulsed Laguerre-Gaussian laser beams and molecular parameters

The Crank-Nicholson numerical scheme and the predictor-corrector method are used to solve the coupled paraxial wave equation (3) and the rate equation (6) in the retarded time frame.The incident laser field has a Laguerre-Gaussian transverse mode(LGpl)distribution

In this study, we only consider the propagation of incident LG pulses with isotropic transverse distribution by settingl=0, namely, the high-order radial modes with zero orbital angular momentums.In this case, the Laguerre polynomials are used as

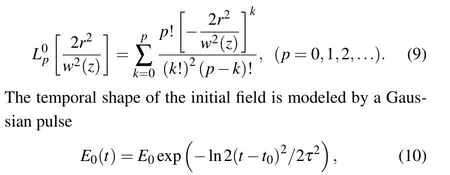
whereτis the half width at half-maximum (HWHM) of the field intensity andt0is the center of the pulse.The duration of the pulse is taken to beτ=10 ns andt0=40 ns.The transmittance of the total pulse energy at the propagation distanceLcan be expressed by

The specific values of the one-photon absorption cross section,the decay rates and the intersystem crossing rate of the molecule are strongly correlated with the experimental conditions.Referring to the experimental data of Ebbesenet al.[47]for the incident wavelength of 650 nm, in numerical simulations we set the absorption cross sections of the C60molecule asσS1S0= 0.20×10-22m2,σSnS1= 9.20×10-22m2, andσT2T1= 14.2×10-22m2; the decay rates and the intersystem crossing rate are 1/ΓT1=280 μs, 1/ΓSn=1/ΓT2=1 ps,1/(ΓS1+Γc)≈1/Γc=1.2 ns.The molecules are assumed to be in the ground state before turning on the field.

3.Results and discussion

3.1.Characteristic time of population transfer

The characteristic time of the population transferτST(t)≡1/γ0(t) between the ground state|S0〉and the lowest triplet state|T1〉primarily depends on the field intensity.It is one of the most important quantities that determines the evolution of the nonlinear optical dynamics in the five-level system studied here.The effective rateγ0(t)in Eq.(6)can be written explicitly in two terms as

One can see from Eq.(12) that since the decay rate of the triplet stateΓT1is much smaller than the intersystem crossing rateΓc,mainly the first term on the righthand side of Eq.(12)contributes.The effective rateγ0(t)increases with the increase in the field intensity, but the saturation effect will be reached when the transition rateγS1S0(t)is close toΓc.

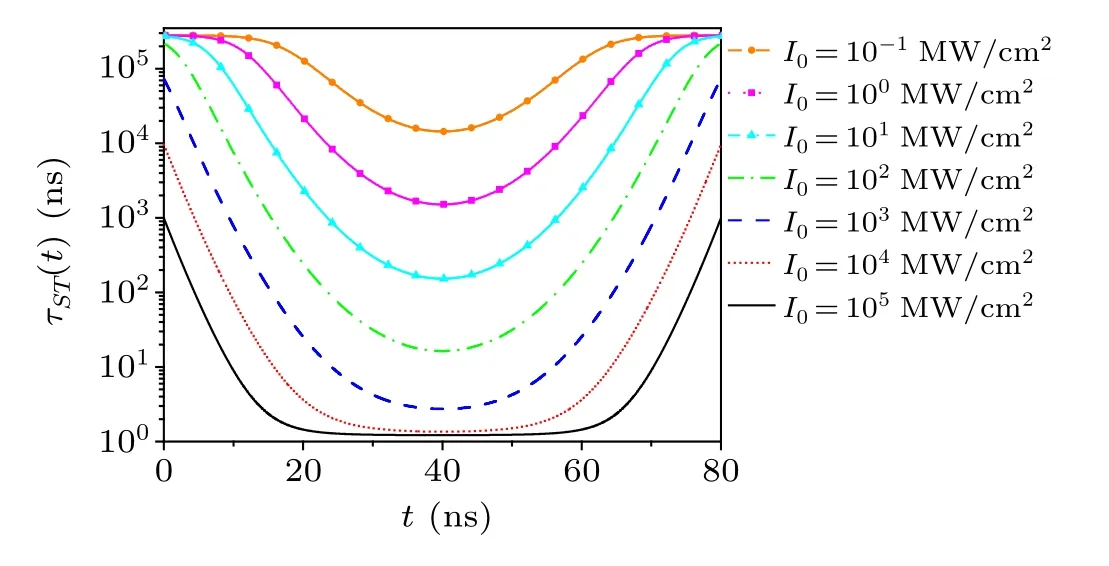
Fig.2.The characteristic time of the population transfer between the singlet and triplet states|S0〉→|T1〉induced by the on-axis field(r=0)of the pulsed LG30 laser beam.The HWHM of the pulse is τ =10 ns centered at t0=40 ns: N=1020 cm-3.

Fig.3.The on-axis population distribution induced by the pulsed Laguerre-Gaussian laser beam at the beginning of propagation.The peak intensity of the field is(a)I0 =10 MW/cm2, (b)I0 =102 MW/cm2, (c)I0=103 MW/cm2,and(d)I0=104 MW/cm2.The other parameters are the same as in Fig.2.

The population transfer induced by fields of different intensity levels are shown in Fig.3.When the field intensity is much smaller than the saturation valueIs= 1.274×103MW/cm2,most of the populations are kept in the ground state and linear absorption of the singlet states mainly occurs(Fig.3(a)).As shown in Fig.2,the increase in the field intensity shortens the characteristic time of the population transfer.When the field is strong enough to promote a remarkable part of the populations to the triplet state(Fig.3(b)),the sequential two-step photon absorption channel (S0→S1)×(T1→T2)becomes important,and the reverse saturable absorption of the triplet states causes the optical power limiting behavior of the field.When the field intensity is further increased to close to the saturation valueIs,the light field transfers almost the entire population to the triplet state (Fig.3(c)).After this, the onephoton absorption of the triplet state dominates and results in obvious population distribution in the upper-level triplet stateρT2(Fig.3(d)).One can further see in Fig.3 that the response speed of the medium to the laser pulse is evidently accelerated by the enhancement of the field intensity.

3.2.Pulse shaping and optical power limiting

When the transverse distribution as well as the propagation effects of the pulsed Laguerre-Gaussian beams (8) are considered, the paraxial wave Eq.(3) coupled with the rate Eq.(6) is solved numerically in the retarded time coordinate system.In our simulations, we neglect the influence of the nonlinear refractive indexδnon the field evolution within a short enough propagation distance.In this case,the linear refractive indexn0of the solvent will not appear explicitly in Eq.(3).

The spatial and temporal distribution of the input thirdorder radial mode LG03field atz=-L/2 and the field distribution after a propagation distance ofL=1.0 mm atz=L/2 are shown,respectively,in Figs.4(a)and 4(b).One can clearly see that each light ring of the pulsed LG30radial mode is strongly reshaped during pulse propagation.The temporal or longitudinal shape of the field is changed from a uniform central symmetric Gaussian pulse to non-symmetric pulses with different shapes, and the pulse durations are cut down due to the strong absorption at the tails of the light rings, as shown in Fig.5.The brighter the initial light ring, the more severe the change in its temporal profile,and the shorter the duration of the output field.Furthermore,the field intensity as well as the pulse energy is drastically attenuated during propagation,especially for the central on-axis light ring with the strongest initial field intensity.The nonlinear field intensity dependent absorption(Eq.(12))also changes the energy ratios of the light rings at different propagation distances,as shown in Fig.4(c).After propagation,the energy ratio of the central light ring falls precipitately,while the energy ratio of the weakest outermost light ring gradually takes the maximum value.

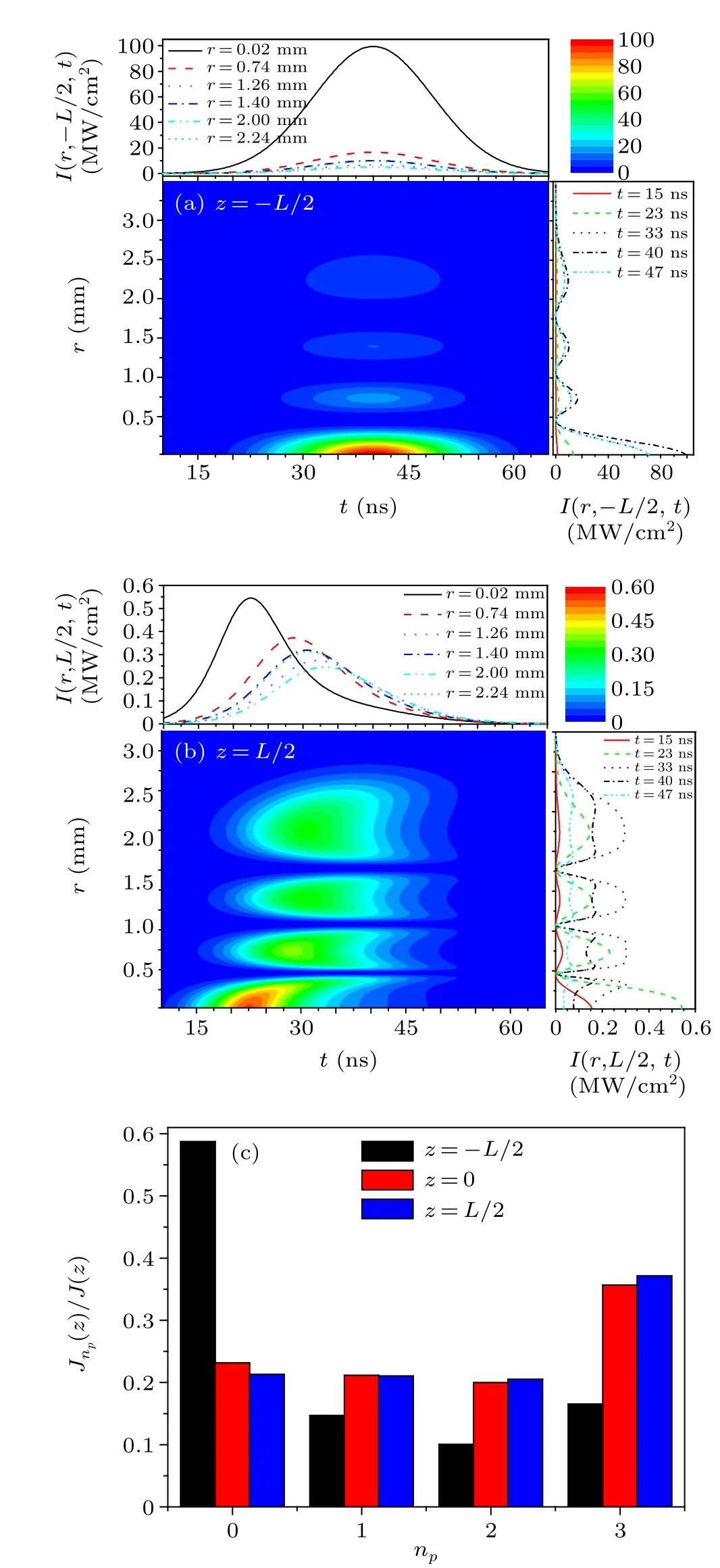
Fig.4.Contour distribution of the field intensity.The color bars give the values of the field intensity in the unit of MW/cm2.(a) The input laser pulse with an LG30 radial mode distribution.(b)The field distribution at z=L/2 after a propagation of L=1.0 mm.The beam waist w0=1.0 mm.The other parameters are the same as in Fig.3(b).(c) The energy ratio of each light ring after different propagation distances of the input LG30 radial mode: np is the index of the light ring; np =0 means the on-axis light ring; np =1 is the first light ring away from the axis,np =2 is the second light ring away from the axis,etc;Jnp(z)is the energy of the np-th light ring;and J(z)is the total pulse energy at position z.

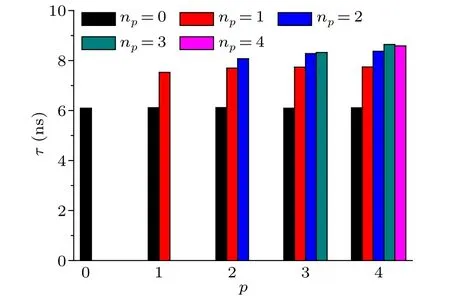
Fig.5.The HWHM of each light ring after a propagation distance of 1.0 mm: p is the radial mode order of the input pulse LGp0,and np is the index of the light ring.The initial HWHM of each light ring is 10 ns.The other parameters are the same as in Fig.4(b).

The main reason for the pulse-shaping effects(Fig.4)is the light intensity dependence of the effective rate(Eq.(12))of population transfer presented in Subsection 3.1.At the leading edge of the pulse, only the weak linear one-photon absorption of the ground singlet state occurs because of the low field intensity there.For the main part of the pulse,due to the increase in the field intensity, the effective rate of population transfer from the singlet to the triplet states increases; therefore,the strong reverse saturable absorption of the triplet states becomes the dominant nonlinear optical process, leading to striking suppression of the high intensity part of the pulse and resulting in the OPL behavior of the field.For the rear part of the pulse,although its input intensity is as low as the leading part, intense triplet state absorption still occurs there due to the accumulation of the population in the triplet state by its anterior part,which causes the asymmetry of the output pulse.In brief,because of the strong reverse saturable absorption effect,obvious OPL behavior is observed for the LG pulse,and the intensity dependence of the effective rate of the population transfer from the singlet to the triplet states results in the asymmetric shaping, energy ratio redistribution and shortening of the output pulse.

3.3.Energy transmittance of different orders of the pulsed LG beams

To clearly show the OPL performance of the incident Laguerre-Gaussian laser beams of different radial orders,the transmittance of the pulse energy as a function of the peak intensity of the incident laser field is presented in Fig.6 for different concentrations of the absorbing molecules.When the initial field intensity is low enough,only the linear singlet state absorption between the ground and the first excited states occurs and the transmittance is consistent with theTS1S0values given in Table 1.

The increase in the input field intensity increases the effective rate of population transfer between the singlet and triplet states and opens the reverse saturable absorption channel of the triplet state.Under these two-step photon absorption conditions,the transmittance of the field drops down fast,and the output field intensity and the corresponding pulse energy are confined below certain values, thus resulting in the OPL behavior of the pulse.From Fig.6(a)one can clearly see that the minimum value of the transmittance is close to but larger than the transmittance of the pure linear triplet state absorption between the two triplet states given in Table 1.After this,the transmittance increases steeply until the upper limit value of one with the further increase in the field intensity, which means the saturation of the population transfer to the triplet states and the breakdown of the OPL performance.Figure 6 also shows that the lower-order LG beam has a faster OPL response and lower energy transmittance,but it also breaks down earlier at lower input field intensity.

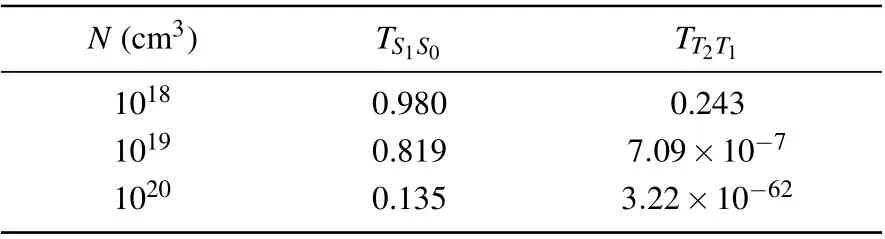
Table 1.Transmittance of pure S0 →S1 singlet state absorption TS1S0 =exp(-NσS1S0L) and pure T1 →T2 triplet state absorption TT2T1 =exp(-NσT2T1L) for different concentrations N of the C60 molecules at the wavelength of 650 nm after propagation of 1 mm.

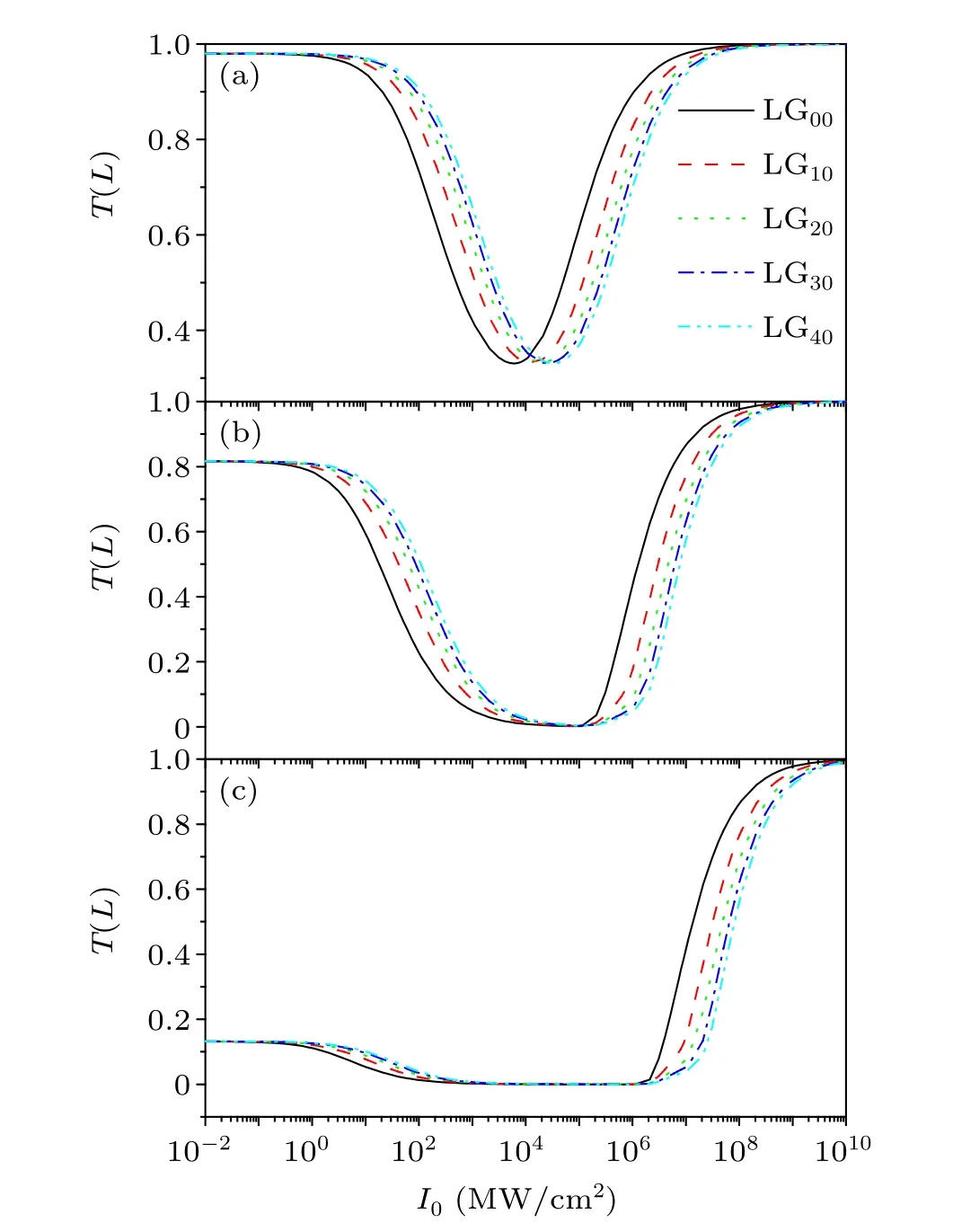
Fig.6.Energy transmittance(12)as a function of the peak intensity of the incident laser field I0.The concentrations of the C60 molecules are(a)N =1018 cm-3, (b)N =1019 cm-3, and(c)N =1020 cm-3.The other input parameters are the same as in Fig.2.

Figure 7 presents the dependence of the energy transmittance on the propagation distanceL.One can see that the transmittance of the field drops down fast at the beginning of propagation due to the intense field-induced fast population transfer;then the decrease in the energy transmittance becomes very slow.This means that there is a characteristic region of the highly efficient OPL performance,and there should be an appropriate compromise between the length of the absorber and the expected value of the energy transmittance.In general,the OPL performance of the pulsed LG beam can be controlled by the concentration of the absorbing molecules and the propagation length,and the LG pulses of different orders show different OPL behavior,which should be taken into account in real applications.

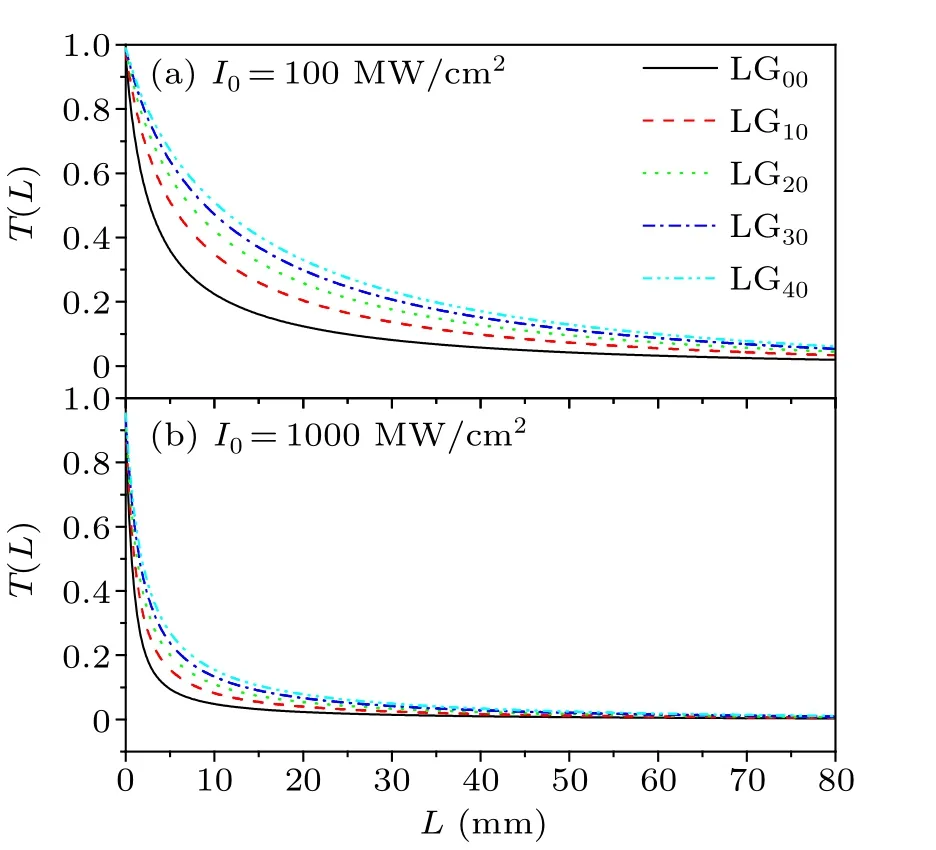
Fig.7.Energy transmittance as a function of the propagation distance L.The incident intensity is (a) I0 = 100 MW/cm2 and (b)I0 =1000 MW/cm2, respectively.The other input parameters are the same as in Fig.6(a).

4.Summary

We studied the nonlinear propagation and the reverse saturable absorption processes of nanosecond Laguerre-Gaussian laser beams of high-order radial modes in C60molecular medium.The adiabatic approximation is used to simplify the population rate equations of the system as the population relaxation times of the excited states are much shorter than the pulse duration and the effective population transfer time from the ground state to the triplet state.

Our results demonstrate that the dynamics of population transfer and pulse propagation are predominantly defined by the effective population transfer time between the ground state and the triplet state, which decreases with the increase in the field intensity.During the propagation of Laguerre-Gaussian laser pulses of high-order radial modes, the spatiotemporal shape of the pulse changes distinctly and the pulse duration is shortened almost by one half.Simultaneously,the pulse intensity decreases dramatically during the course of propagation,and the peak intensity of the light field is reduced by several orders of magnitude,thus displaying extraordinary optical power limiting behavior.The lowerorder pulsed Laguerre-Gaussian beam shows better optical limiting performance with a smaller energy transmittance, but its optical limiting behavior also breaks down earlier at a relatively weaker incident field intensity than the higher-order ones.This study provides valuable information for future experimental studies of the nonlinear optical properties of high-mode laser fields,and paves the way for the application of high-mode laser fields in optical power limiting processes.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos.11974108 and 11574082), Fundamental Research Funds for the Central Universities (Grant No.2021MS046), and the Natural Science Foundation of Shandong Province,China(Grant No.ZR2019MA020).