First-principles prediction of quantum anomalous Hall effect in two-dimensional Co2Te lattice
Yuan-Shuo Liu(劉元碩), Hao Sun(孫浩), Chun-Sheng Hu(胡春生),Yun-Jing Wu(仵允京), and Chang-Wen Zhang(張昌文)
School of Physics and Technology,University of Jinan,Jinan 250022,China
Keywords: quantum anomalous Hall effect,spin-polarizationm Chern insulator,first-principles calculations
1.Introduction
In 1988 Haldane theoretically predicted the quantum anomalous Hall effect (QAHE),[1,2]which is one of the typical representatives of topological phase.QAHE refers to the phenomenon of anomalous Hall conductivity quantization due to the coupling between spin-orbit coupling(SOC)and intrinsic magnetization.This is different from the spin-degenerate chiral edge state integer quantum Hall effect, whose timereversal symmetry (TRS) is broken by an external magnetic field.The spinless/spinful chiral edge state is an important hallmark of QAHE, which originates from the bulk topology of the quantum anomalous Hall(QAH)system.Precisely because of its dissipative chiral edge state,QAHE is ideal for the transmission of electronic and spintronic devices,can be used to make a new generation of low-power or even power-free electronic devices and provide the right platform for studying new quantum phenomena such as topological electromagnetic effects and topological superconductivity.So far, there have been many schemes to implement QAHE proposed.The first observable QAHE was in Cr-dopedX2Te3(X=Bi, Sb)films at 30 mK.[3]Similar to the magnetic adatoms on nonmagnetic Dirac materials,[4]the enhanced SOC of QAHE can be achieved by depositing atomic layers of heavy elements(MnX;X=S,Se,Te)on the surface of magnetic insulators.[5]It is clear that the low observed temperature is far from practical application.Some articles claim that magnetic dopants will cause uneven magnetic distribution, which is not conducive to the occurrence of QAHE, resulting in low observation temperature.[6,7]For this reason,the method of increasing the observation temperature has become to search for intrinsically magnetic topological insulators, and non-dissipative electronic conduction at room temperature is a key research direction in condensed matter physics science.[8,9]Spin can be actively manipulated in spin-polarized transport-based devices, such as the spin-FET proposed by Datta and Das.[10]Two-dimensional (2D) Dirac semimetal materials have received high attention because of higher magnetoresistance,higher carrier mobility and topologically non-trivial properties, which originate from characteristic linear band dispersion near the Fermi surface and Massless fermions.In search of new 2D Dirac materials, a great deal of research has been carried out,both experimentally[11,12]and theoretically.[13-17]This is a novel ferromagnetic system with 100% spin polarization, and its conduction around the Fermi energy level is driven by one of the spin components, while the other has the suitable gap, which enables reduced device size and nonvolatile memory.[18-20]The semimetal containing the Dirac cone in the conductive channel is the Dirac semi-metallic material,which has potential application prospects in high-speed spintronic devices.
Chern insulators are also known as quantum anomalous Hall insulators.[21-23]When Dirac semimetals have strong spin orbital couplings,they can lead to Chern insulators[24-26]or valley electron materials.[10,27-29]When there is no external magnetic field, Chern insulators exhibit a QAHE with quantized Hall conductivitye2/h, enabling dissipative-free transport of chiral edge channels in novel electronic devices.Up to now, many QAHE candidates have been proposed, in particular magnetically doped or functionalized topological insulators whose lattice shapes are honeycomb or square.[4,30-33]Relatively speaking,the monolayer(ML)Co2Te structure proposed in this paper is relatively new,which may provide some preparation for future work on this type of structure.
In this paper, we demonstrate ML Co2Te as a new QAH stage based on the first-principles calculations.In this system,each spin-polarized Co cation contributes a magnetic moment of 2μBoriginating from the d orbital.The band structures with/without SOC are calculated,indicating that the ML Co2Te structure is a non-trivial QAH insulator with a bandgap of 96 meV.Then, by calculating the edge states and anomalous Hall conductance of ML Co2Te, it is verified that it has the non-zero Chern numberC= 1.At the same time, the Curie temperature of this material is confirmed to reach 573 K through Monte Carlo (MC) simulations of the unit cell.Our discovery provides a promising material for the practical application of QAHE in spintronics.
2.Computational details
We carry out the approach of first-principles calculations as implemented in Viennaab initiosimulation package based on the density-functional theory (DFT).The projector-augmented-wave (PAW) potential,[34,35]Perdew-Burke-Ernzerhof (PBE) exchange-correlation functional,[36]and the plane-wave basis with a kinetic energy cut of 400 eV are employed.The Brillouin zone is sampled by using an 9×9×1 Gamma-centered Monkhorst-Pack grid, and SOC is included by a second variational procedure on a fully selfconsistent basis.Since the correlation effects of Co-3d electrons, we employed the GGA+Umethod and set theU=5.0 eV(J=0.0 eV).In the process of structure optimization,the positions and lattice parameters of all atoms have been completely relaxed, and the maximum force allowed on each atom is less than 0.001 eV/°A.What is more,the Berry curvature is calculated by the maximally localized Wannier function method implemented in WANNIER90 package,[37,38]and Cod orbitals are chosen as projected orbitals.[39]Finally,we use the iterative Green’s function method to study the edge state to further prove its QAHE.[40]
3.Results and discussion
The geometry of ML Co2Te is depicted in Fig.1(a).The calculated lattice constant isa=b= 4.6037 °A.Each Co atom is surrounded by three Te atoms, and the Co-Te-Co has a bond angle of 120°.Firstly, we calculate the formation energy to verify the stability of the structure, ΔEf=ECo2Te-2ECo-ETe, whereECo2Te,ECo, andETeare the total energies of Co2Te, Co, and Te crystals, respectively.The resulting value,-1.83 eV/atom,is in the same order of magnitude as those of ML C3Ca2(-2.60 eV/atom)[41]and graphene(-8.66 eV/atom),[42]which indicates that ML Co2Te is a relatively strong bonding planar network.We also calculate the electronic localization function(ELF)and results are depicted in Fig.1(b).The value of ELF ranges from 0 to 1, and can usually be used to determine the characteristics of electronic bonds and the degree of electronic localization, where ELF=0,0.5,1 denote no electron distribution,homogeneous electron gas, and complete local electrons at specific sites,respectively.In the figure, we can clearly see that the electrons are mainly located around the Te atoms,and only a small amount is located near the Co atoms,which indicates that the typical ionic bond between Co and Te is formed.The calculation of the calculated elastic constant also has important reference significance for checking the mechanical stability of the structure.Using Voigt notation, the elastic tensorCwithD6hpoint-group symmetry for 2D materials can be reduced into
The calculated results show thatC11andC12are 324.7143 kbar(1 bar=105Pa) and 252.1783 kbar, respectively.The calculatedCijsatisfy the Born criterion of mechanical stability:C11>0 andC11-C12>0,confirming the mechanical stability of ML Co2Te with the potential for experimental preparation and room temperature survival.

Fig.1.(a)Top and side views of ML Co2Te.The rhombus shows the unit cell.Among them, blue balls and brown balls represent Co atoms and Te atoms, respectively.(b) ELF image of ML Co2Te viewed from the side.(c)First Brillouin zone with high symmetry points Γ,M,and K.
To find the preferred magnetic ground state of the system, we have considered three possible configurations of the unit cell, including FM, AFM, and NM, as shown in Fig.2(a).The calculation dates show that the energy of FM state(ΔEFM=EAFM-EFM)is 1.301 eV and 4.913 eV lower than that of AFM and NM states,respectively.The total magnetic moment of each unit of ML Co2Te single molecule layer is predicted to be 4μB,of which Co atoms contribute the vast majority,which is a low-bucked honeycomb lattice.The magnetocrystalline anisotropy energy(MAE)is defined as the energy required to rotate the magnetization from the easy axis to the hard axis of a ferromagnet,which determines the difficulty of spin flipping.It plays a critical role in establishing 2D FM ordering.For the lattice, the MAE(θ,φ)in any direction(θ,φ)is as follows:
whereK1andK2are system-dependent anisotropy constants andθis the azimuthal angle of rotation.We can find in the calculation that MAE(θ,φ)has almost nothing to do with the in-plane azimuthφ, that is to sayK3=0.The results show that the MAE(θ,φ)reaches its minimum value in the in-plane axis,demonstrating that this structure is in-plane magnetized,as depicted in Fig.2(c).

Fig.2.(a)Different magnetic configurations.(b)The variation of the magnetic moment with temperature for each cell with temperature according to MC simulations.(c) Magnetocrystalline anisotropy energy (MAE) for Co2Te by rotating the spin with in z-x and x-y planes, respectively.The orange line in panel represents the fitted curves.MAE(θ)=K1 cos2 θ+K2 cos4 θ and MAE(θ)=0,respectively.
In the practical application of spintronic devices, the Curie temperature (Tc) is also an important parameter.It is easy to adjust the direction of the magnetic axis to be outplane.At this time,the Heisenberg model we use to calculate the Curie temperatureTcis
in whichSi/SjandSziare the spin vectors of each Co atom and the spin component parallel to thezdirection,J=6.78 meV andA=-115.31μeV are the nearest neighbor exchange parameter and MAE.TheJwith normalized spin vector can be attained by comparingEAFMandEFM,which has the following expression:J=(EAFM-EFM)/2zS2,wherezis the number of the nearest neighbor Co atoms,andSis the spin value of a single Co atom.AndAis calculated fromA=(E100-E001)/S2.To make the FM-paramagnetic transition clearer,we next calculate the heat capacity(Cv)as follows:
Here, ΔETis the change of the total energy as the temperature changes fromTtoT+ΔT.Figure 2(b)shows the variation of the magnetic moment of each unit cell with temperature.It can be noticed that the magnetic moment starts to decrease sharply from 4μBto 0 K at 573 K,which means state transition from FM to AFM.This temperature is much higher than that observed in recent years for ML CrI3(45 K)[43]and Cd2N3(225 K),[44]so this system is expected to be a potential candidate for high-temperature QAHE in spintronic applications.
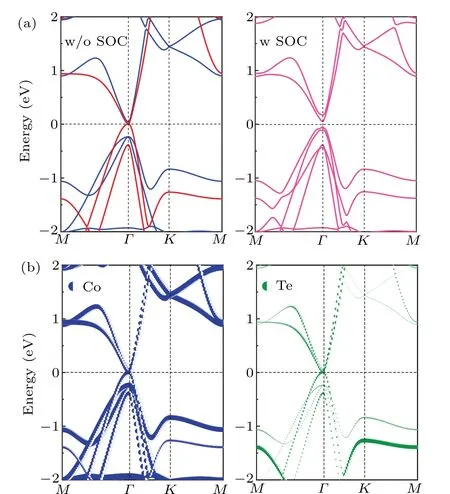
Fig.3.(a) The electronic band structures of ML Co2Te without (w/o) and with (w) SOC, red and blue lines of the graph without SOC represent the spin-up and spin-down channels,respectively.(b)Energy band composition analysis of Co and Te atoms in ML Co2Te.
Next,we will explore the electronic nature of this aspect.The structure of the single-molecular-layer spin polarization band of ML Co2Te is depicted in Fig.3(a).We can see that the spin-up channel and the spin-down channel are not related without considering the SOC, where the former has no bandgap, but the latter opens a large bandgap of 272 meV.Such single-spin channel hybridizations differ from conventional QAHE, which arise from hybridizations between two different spin states near the Fermi surface.The consideration of SOC makes the system of ML Co2Te open a sizable bandgap of 96 meV at PBE level towards spin-up channel,which provides the possibility to achieve QAHE.
One prominent feature for realization of QAHE is band topology.To further determine the components of atoms near Fermi level,we plot the atom-resolved band structures of ML Co2Te.It can be observed from Fig.3(b)that the band structure of the spin channel near the Fermi surface are mainly contributed by the magnetic Co atoms.Then we narrow calculation interval to obtain the orbital-resolved band structure of Co atoms near the Fermi surface.As depicted in Figs.4(a) and 4(b),we can apparently find that the band structure is considerably contributed by Co-dx2-y2/dxyand Co-s orbitals.With considering SOC,as depicted in Figs.4(c)and 4(d),part of the orbitals of Co-dx2-y2and Co-dxyare interchanged in conduction band and valence band,respectively.This orbital reversal indicates the existence of band topology of ML Co2Te.And large gap of 96 meV due to SOC are indicating a wide platform of anomalous Hall conductivity.
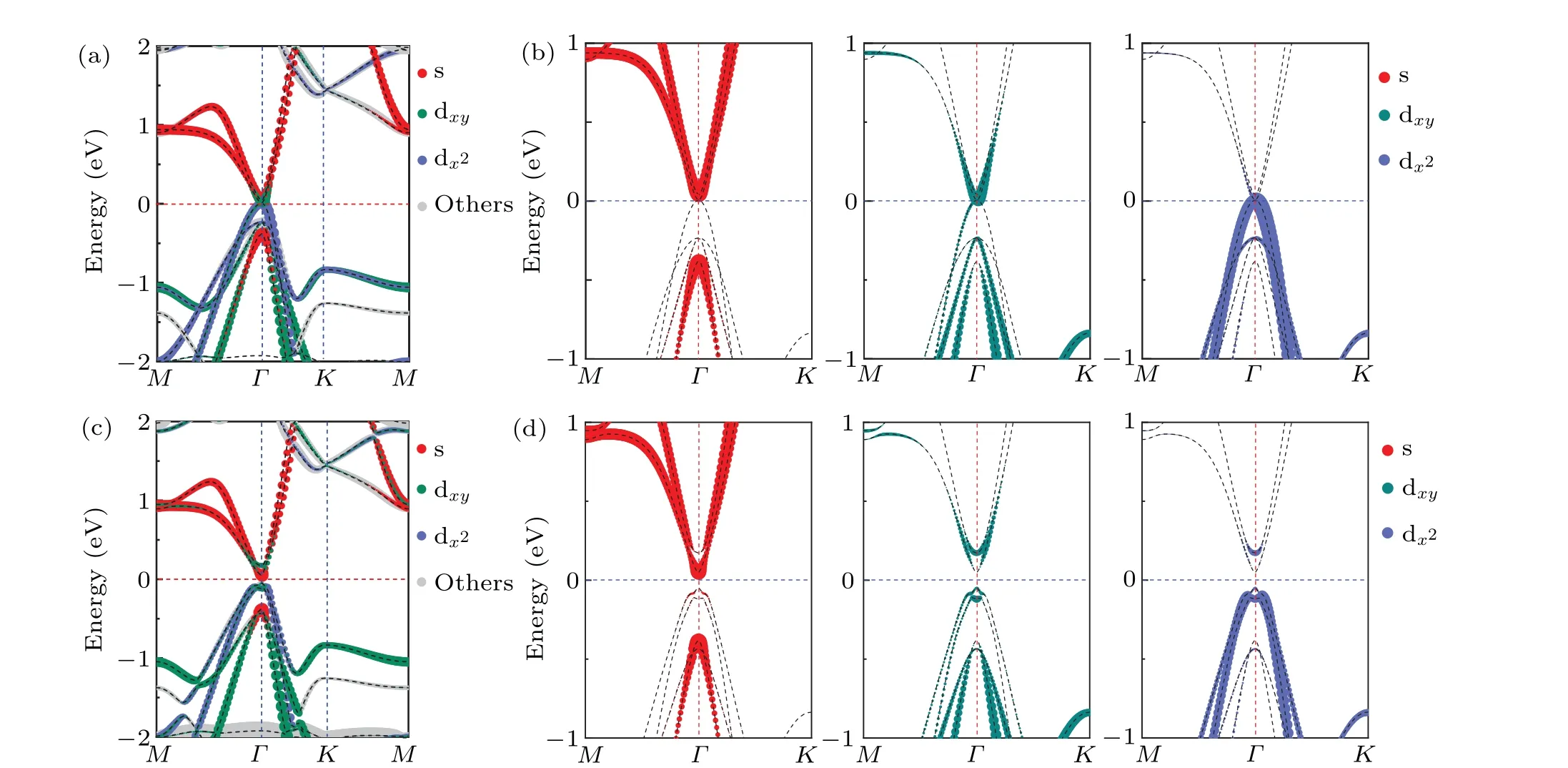
Fig.4.(a)The main orbitals of Co atoms without SOC.(b)The s,dxy,and dx2-y2 orbitals of Co atoms without SOC.(c)The main orbitals of Co atoms with SOC.(d)The s,dxy,and dx2-y2 orbitals of Co atoms with SOC.The gray part in the figure represents the contribution of Co atoms on other orbitals(px,py,pz,dyz,dxz,dz2).
The Kubo formula[45,46]states that the QAH phase can be determined using the Chern number (C) calculated from thek-space integral of the Berry curvature(Ω(k))of all states below the Fermi level,as shown below:
Here,Enis the eigenvalue of the Bloch function|Ψnk〉,fnis the Fermi-Dirac distribution function, andνxandνyare the velocity operators.Figure 5(c)shows the Berry curvature for the whole valence bands along the high symmetry directions in momentum space.By integrating(Ω(k))over the first Brillouin Zone,the Chern number(C)
is equal to 1.Thus, the anomalous Hall conductivity shows a quantized charge Hall plateau, with valueσxy=e2/h, located in the insulating gap of the spin-up Dirac cone,as shown in Fig.5(d).Such a presence of a topological protection chiral edge state is a prominent feature of QAHE.We computed the edge states of a semi-infinitely large ML Co2Te to reveal the non-trivial topological properties of the system at a deeper level.Since the existence of chiral the edge state is completely determined by the bulk topology,we calculated the band structure of the ML Co2Te edge using the Wannier charge center method,[47]where the maximally localized Wannier function is constructed from the WANNIER90 TB package.[48]Figure 5(a) shows the fitted DFT and TB bands, and it can be seen that the energy bands fitted by Wannier and PBE are very similar.Notably, the texture of edge state in Fig.5(b) shows that it is fully spin-polarized in thezdirection, which indicates the semi-metallic nature of this material.The edge states connecting the valence and conduction bands can clearly be seen from the figure traversing the insulating gap of spin channel,which confirms its non-trivial topological properties.The semi-metallic behavior exhibited here differs from that of conventional semimetals, which may highly suppress spin polarization when SOC is considered.[49-52]
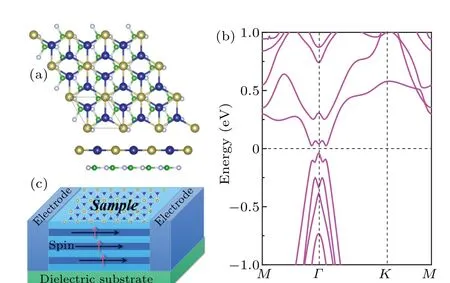
Fig.6.(a) Top and side views of the epitaxial growth of the Co2Te lattice on BN substrate.The interlayer distance is 3.66 °A.Among them, green balls and gray balls represent B atoms and N atoms, respectively.(b) The corresponding energy band structure Co2Te/BN.(c) A model of a feasible topological field transistor device.The ML Co2Te is deposited on a dielectric substrate sandwiched between two electrodes.The red arrows represent the spin direction of the electron in the edge state,while black arrows represent the electron transport direction.
Finally, a key point is whether the QAHE of ML Co2Te can be maintained on the substrate, which is unavoidable in device applications.As we all know, single-layer BN material is chemically inert and not easy to combine with other molecules, so we use it as a protective film for ML Co2Te growth.So, the Co2Te/BN has been constructed, as shown in Fig.6(a).In this structure, the QAH effect in the Co2Te lattice is essentially maintained.Figure 6(b) shows the calculated band structure of SOC.It can be seen that there is still a SOC-induced band gap atΓpoint near the Fermi level,which is consistent with what we would expect.Considering that 2D h-BN substrate electrically insulates the QSH layer adjacent to ML Co2Te and protects the parallel spiral edge channel from interlayer hybridization gaps, Co2Te/BN is an ideal superconductor to support dissipative charge/spin transport in quantum devices.It indicates that it is feasible to construct quantum devices using Co2Te/BN heterostructures, as depicted in Fig.6(c).
4.Conclusion
In summary, we calculated electronic band structure of ML Co2Te based on first-principles, characterized by a large gap in the spin-down channel and a Dirac cone in the spin-up channel.When considering spin-orbit coupling, the spin-up channel opens a 96-meV gap, and the non-zero Chern number and edge state features further reveal its topological nontriviality.The Curie temperature is 573 K through MC simulations.Thus, these results suggest that ML Co2Te as a material with QAHE provides a promising platform for the fabrication of dissipation-free, all-spin-polarized and high-speed spintronic devices.
Acknowledgements
Project supported by the Taishan Scholar Program of Shandong Province,China(Grant No.ts20190939),the Independent Cultivation Program of Innovation Team of Jinan City(Grant No.2021GXRC043),and the National Natural Science Foundation of China(Grant No.52173238).
- Chinese Physics B的其它文章
- Analysis of cut vertex in the control of complex networks
- Atlas of dynamic spectra of fast radio burst FRB 20201124A
- Investigating the characteristic delay time in the leader-follower behavior in children single-file movement
- Micro-mechanism study of the effect of Cd-free buffer layers ZnXO(X =Mg/Sn)on the performance of flexible Cu2ZnSn(S,Se)4 solar cell
- Thermally enhanced photoluminescence and temperature sensing properties of Sc2W3O12:Eu3+phosphors
- Heterogeneous hydration patterns of G-quadruplex DNA

