Low-Density Parity-Check Codes: Highway to Channel Capacity
Liyuan Song,Shuyan Yu,Qin Huang,*
1 Fujian Provincial Engineering Technology Research Center of Photoelectric Sensing Application,Key Laboratory of OptoElectronic Science and Technology for Medicine of Ministry of Education,Fujian Normal University,Fuzhou 350007,China
2 School of Electronic and Information Engineering,Beihang University,Beijing 100191,China
Abstract: Low-density parity-check (LDPC) codes are not only capacity-approaching,but also greatly suitable for high-throughput implementation.Thus,they are the most popular codes for high-speed data transmission in the past two decades.Thanks to the low-density property of their parity-check matrices,the optimal maximum a posteriori probability decoding of LDPC codes can be approximated by messagepassing decoding with linear complexity and highly parallel nature.Then,it reveals that the approximation has to carry on Tanner graphs without short cycles and small trapping sets.Last,it demonstrates that welldesigned LDPC codes with the aid of computer simulation and asymptotic analysis tools are able to approach the channel capacity.Moreover,quasi-cyclic(QC) structure is introduced to significantly facilitate their high-throughput implementation.In fact,compared to the other capacity-approaching codes,QCLDPC codes can provide better area-efficiency and energy-efficiency.As a result,they are widely applied in numerous communication systems,e.g.,Landsat satellites,Chang’e Chinese Lunar mission,5G mobile communications and so on.What’s more,its extension to non-binary Galois fields has been adopted as the channel coding scheme for BeiDou navigation satellite system.
Keywordst: LDPC codes; sparsity; high-speed;message-passing;cycles;trapping sets;quasi-cyclic
I.INTRODUCTION
In his PhD thesis in 1960,Gallager[1]invented a class of good codes specified by parity-check matrices containing mostly ‘0’s and only few ‘1’s.It has been shown that these codes perform very well under his proposedmessage-passing(MP)decoding.However,this landmark work was forgotten for three decades,since the decoding was too complex for computational capability of that time[2].As shown in the brief timeline in Figure 1 of LDPC codes,a significant contribution during these decades is that Tanner[3]introduced bipartite graphs consisting of two types of nodes connected by edges,called Tanner graphs,to graphically represent LDPC codes.
Until the late 1990s,MacKay [4,5] designed binary codes with very sparse parity-check matrices and showed by simulations that those codes can approach nearchannel capacity,i.e.,Shannon limits,with the optimalmaximum a posteriori probability(MAP)decoding.Later,Wiberg [6,7] proved that the MP decoding performs exactly MAP over Tanner graphs free of cycles.Soon people realized that these capacityapproaching codes are in fact Gallager’s LDPC codes.
In general,it is very hard to perform the MAP decoding over general linear codes.However,the MP decoding allows LDPC codes to achieve the performance of MAP decoding with linear complexity.Moreover,the highly parallel nature of MP promises the possibility of implementing decoders with highthroughput.It makes LDPC codes extremely attractive for communication systems,considering decoders usually consume most of the computational resources of baseband chips.
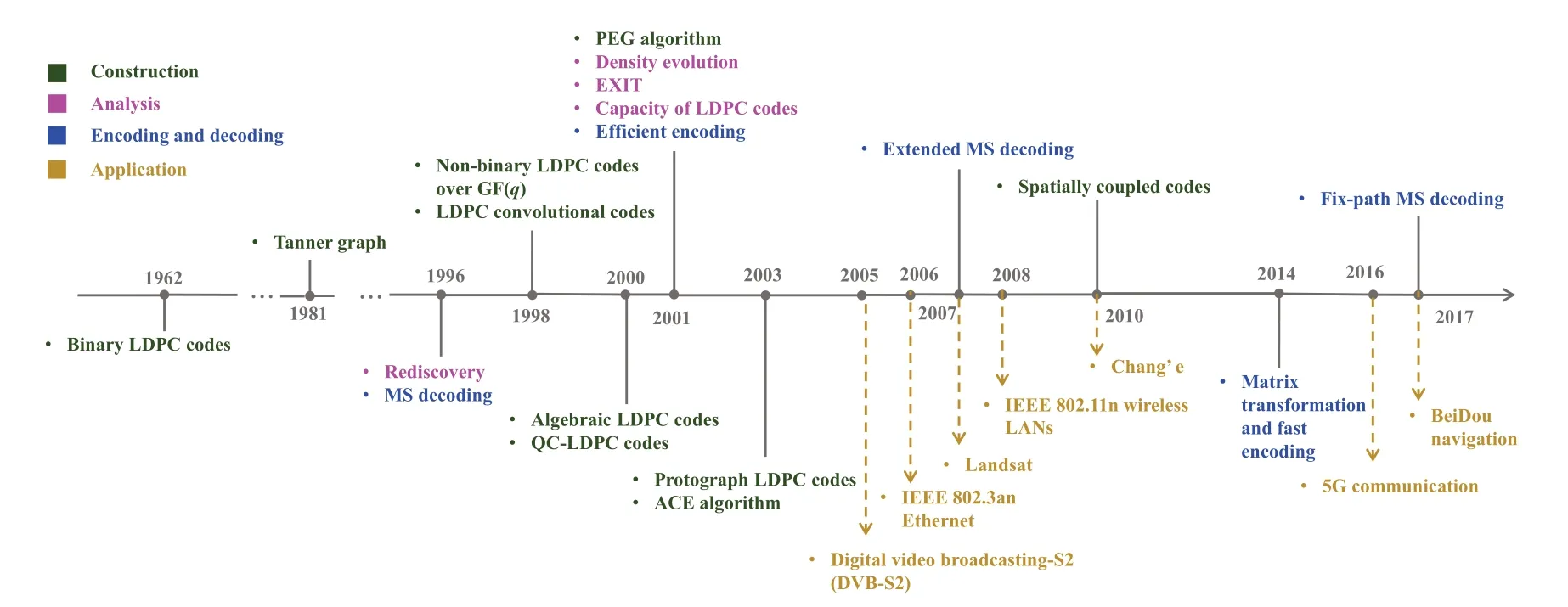
Figure 1.A brief timeline of LDPC codes.
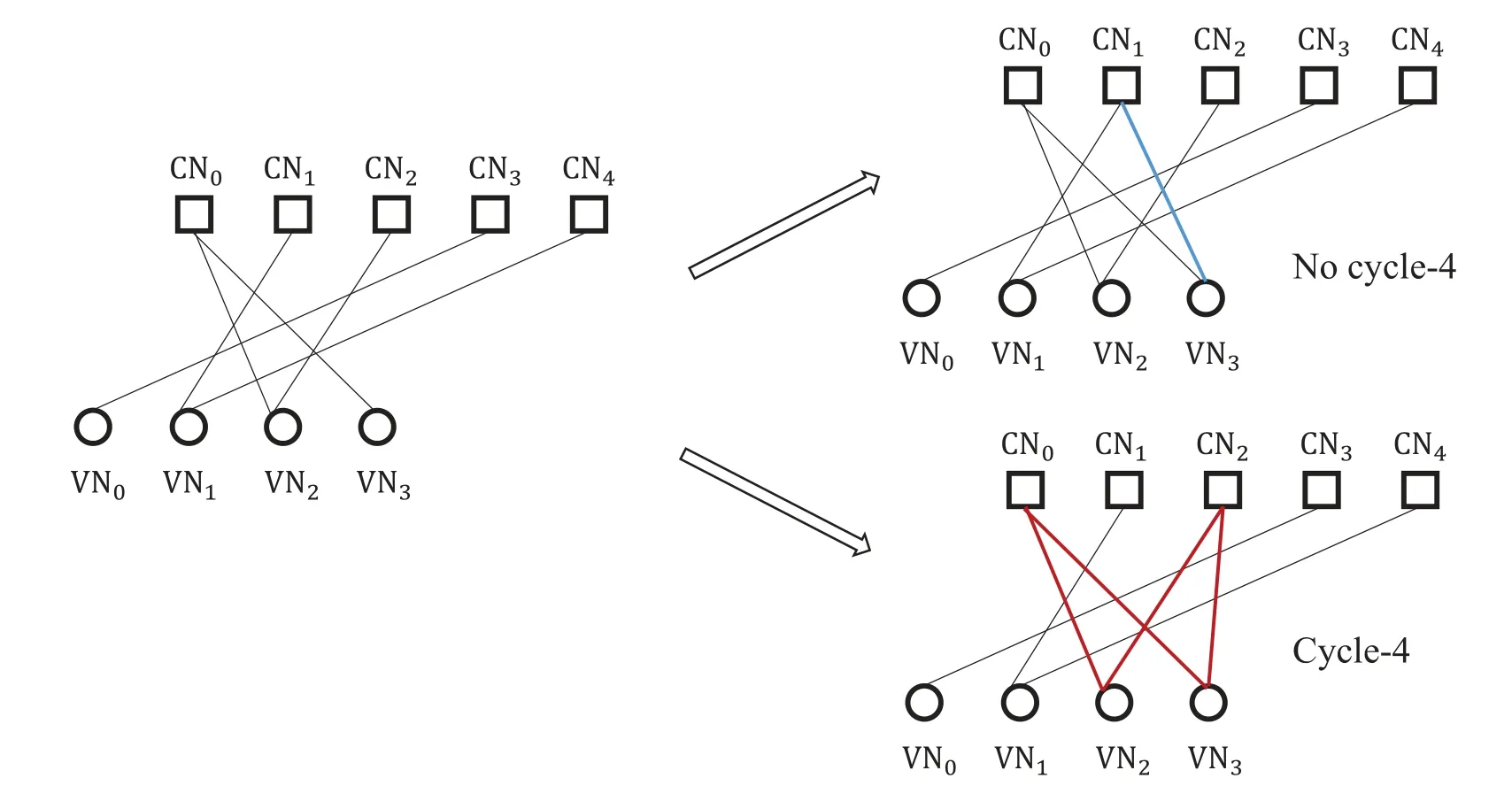
However,it remained challenging in practice to achieve good error performance due to short cycles in Tanner graphs of LDPC codes.Linet al.[8—11]constructed a variety of algebraic LDPC codes based on finite geometries and finite fields.The introduction ofrow-column constraint(RC constraint)guarantees that there are no cycles of length 4 in Tanner graphs.Moreover,these algebraic LDPC codes usually havequasicyclic(QC)structure,which is very important for implementation as we will mention later.The other construction is based on computer search over graphs.Huet al.[12,13]gave aprogressive edge-growth(PEG)algorithm to construct Tanner graphs in an edge-byedge manner.Later,it was generalized for constructing QC-LDPC codes[14].
Besides short cycles,Richardson pointed out that there are two another vital aspects of Tanner graphs which can affect error performance,trapping sets[15]and degree distributions [16].Trapping sets are the combinations of a relatively small number of errors that lead MP to failure.Usually they induce subgraphs lacking connections to the whole graphs.Later,several methods based on algebraic structure[17]or computer search [18] were proposed to avoid small trapping sets.Degree distributions describe the number of edges connected to nodes in Tanner graphs.Asymptotic analysis tools,density evolution[16]as well as its approximation,extrinsic information transfer(EXIT)chart[19],demonstrate that long LDPC codes with optimized degree distributions can approach the channel capacity.
If we implement the MP decoders of LDPC codes in hardware,it comes to complex routing due to“random-like” connected edges in Tanner graphs.It not only costs a large amount of chip area,but also significantly increases the computation delay[20].Thus,many researchers focused on a class of structured LDPC codes,QC-LDPC codes,whose parity-check matrices consist of circulants.The QC structure not only alleviates the wire routing problem by simple shift registers,but also brings regularity of paritycheck matrices to facilitate high-throughput design.Moreover,QC-LDPC codes have comparable performance to their random-like counterparts.
As a result,QC-LDPC codes have been widely applied in numerous applications such as satellite communications,space communications,mobile communications and so on.For example,the (8176,7156)QC-LDPC code [21],designed by Linet al.,has been used inLand Remote-sensing Satellite 8(Landsat 8) with a significantly higher data transmission rate than previous Landsat missions.Moreover,QCLDPC codes have been used in Chang’e Chinese lunar mission,which significantly reduce the antenna area.Besides,QC-LDPC codes have been used in various communication standards,e.g.,IEEE 802.11n wireless LANs.In 2016,QC-LDPC codes have been recommended byThird Generation Partnership Project(3GPP) as the channel coding scheme for theenhanced mobile broadband(eMBB)data channel in 5G communication [22],where the peak data download rate is up to 20 Gbps.
In addition,Davey and MacKay [23] extended binary LDPC codes tonon-binary(NB)-LDPC codes over finite fields GF(q).Though they have been demonstrated to outperform their binary counterparts,their MP decoding is too complex for practical applications.Then,a variety of low complexity decoding algorithms [24—28] have been proposed to seek better trade-offs between performance and complexity.Recently,NB-LDPC codes have been adopted as the channel coding scheme for BeiDou navigation satellite system[29,30].
The rest of this paper is organized as follows.Section II reviews the basic principles of LDPC codes.Constructions of LDPC codes are presented in Section III.Section IV gives several typical applications of LDPC codes.In Section V,NB-LDPC codes are reviewed.Conclusions are drawn in Section VI.
II.PRINCIPLES OF LDPC CODES
This section starts from the matrix and graphical representations of LDPC codes.Then,the MP decoding is presented.Cycles,degree distributions and trapping sets are comprehensively discussed,as well as their importance for LDPC with the MP decoding.
2.1 Parity-check Matrices and Tanner Graphs
There are two different methods to represent LDPC codes: matrix representation and graphical representation.
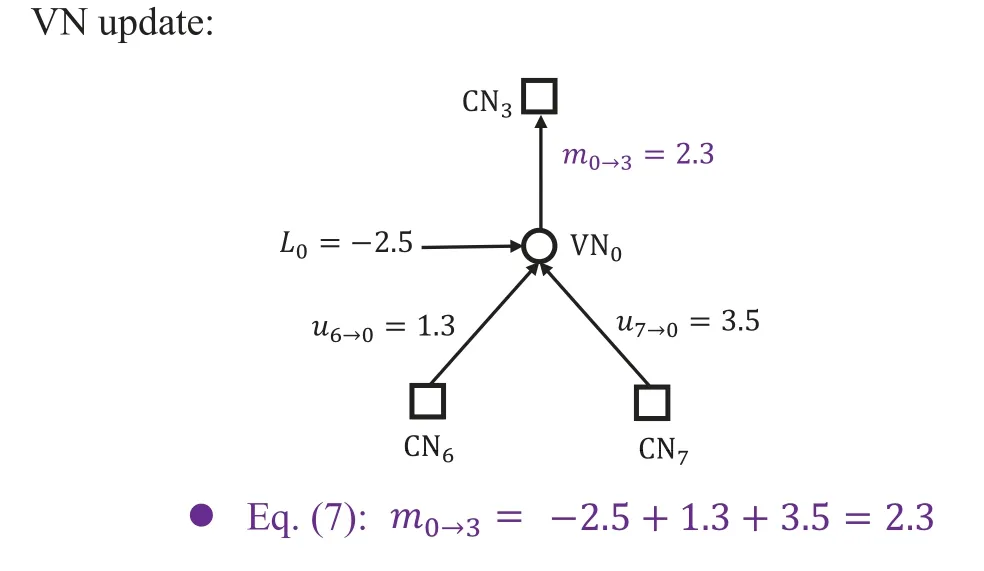
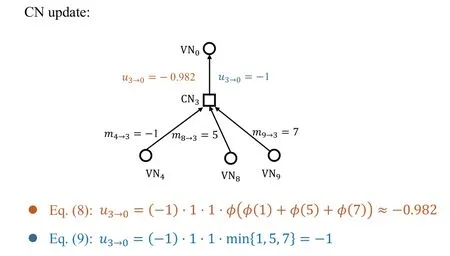
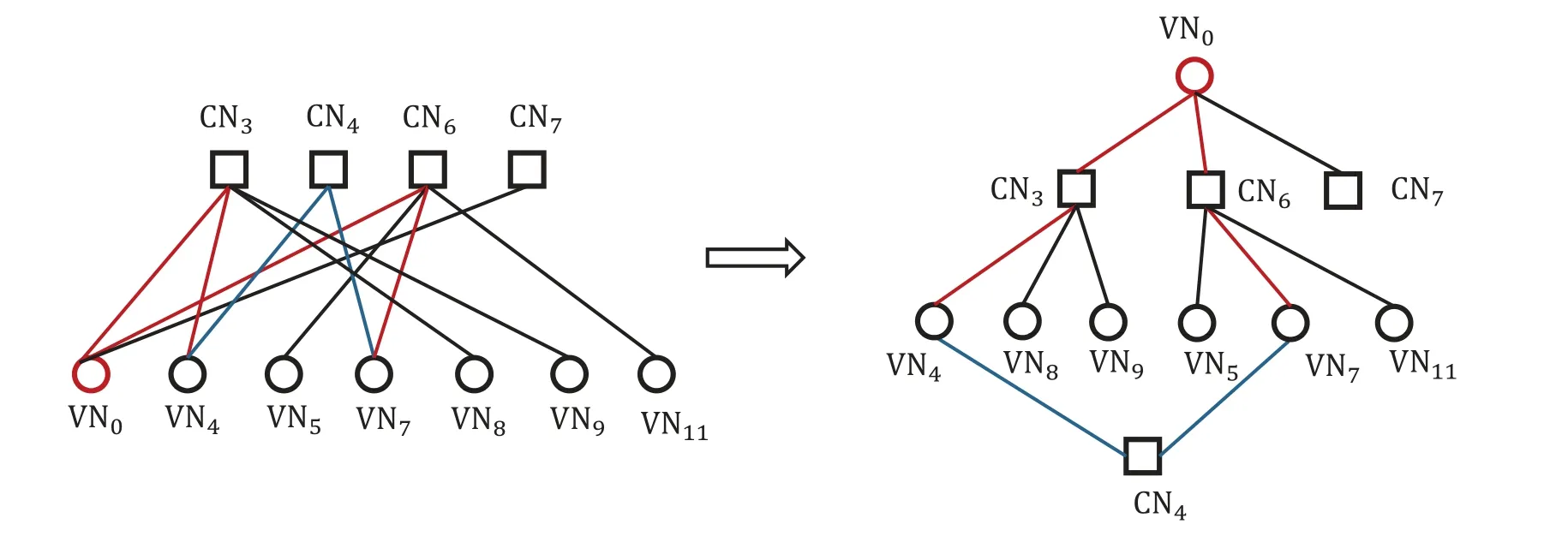
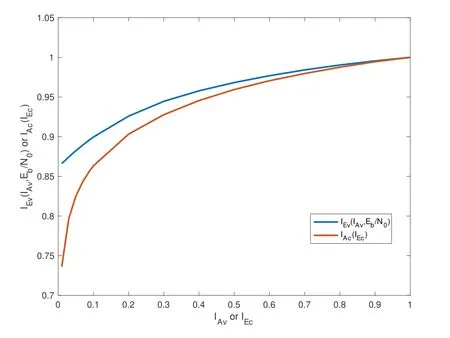
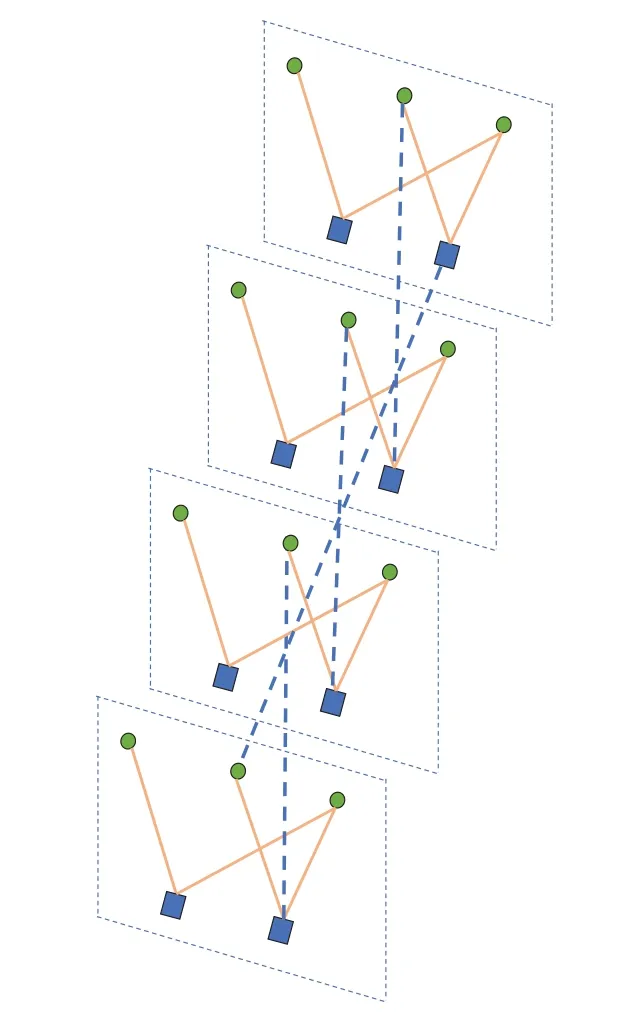
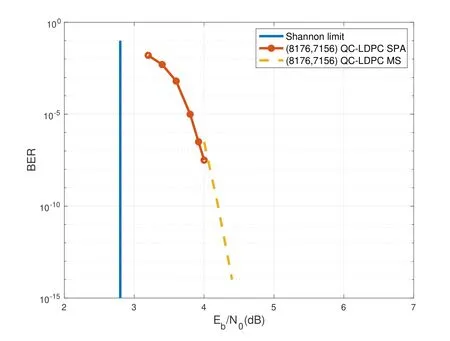
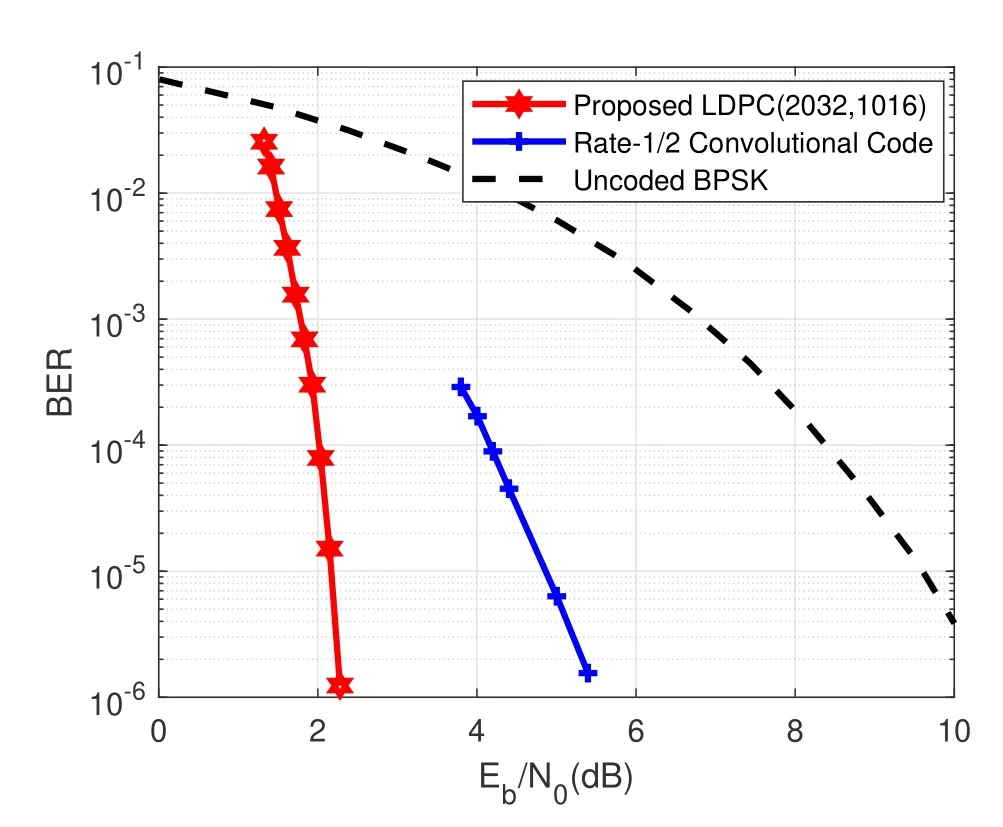
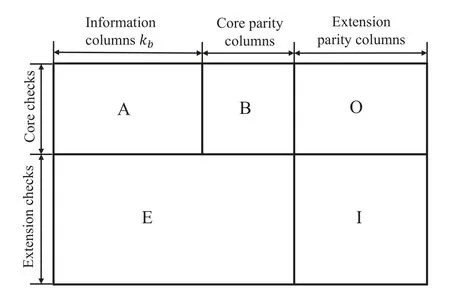
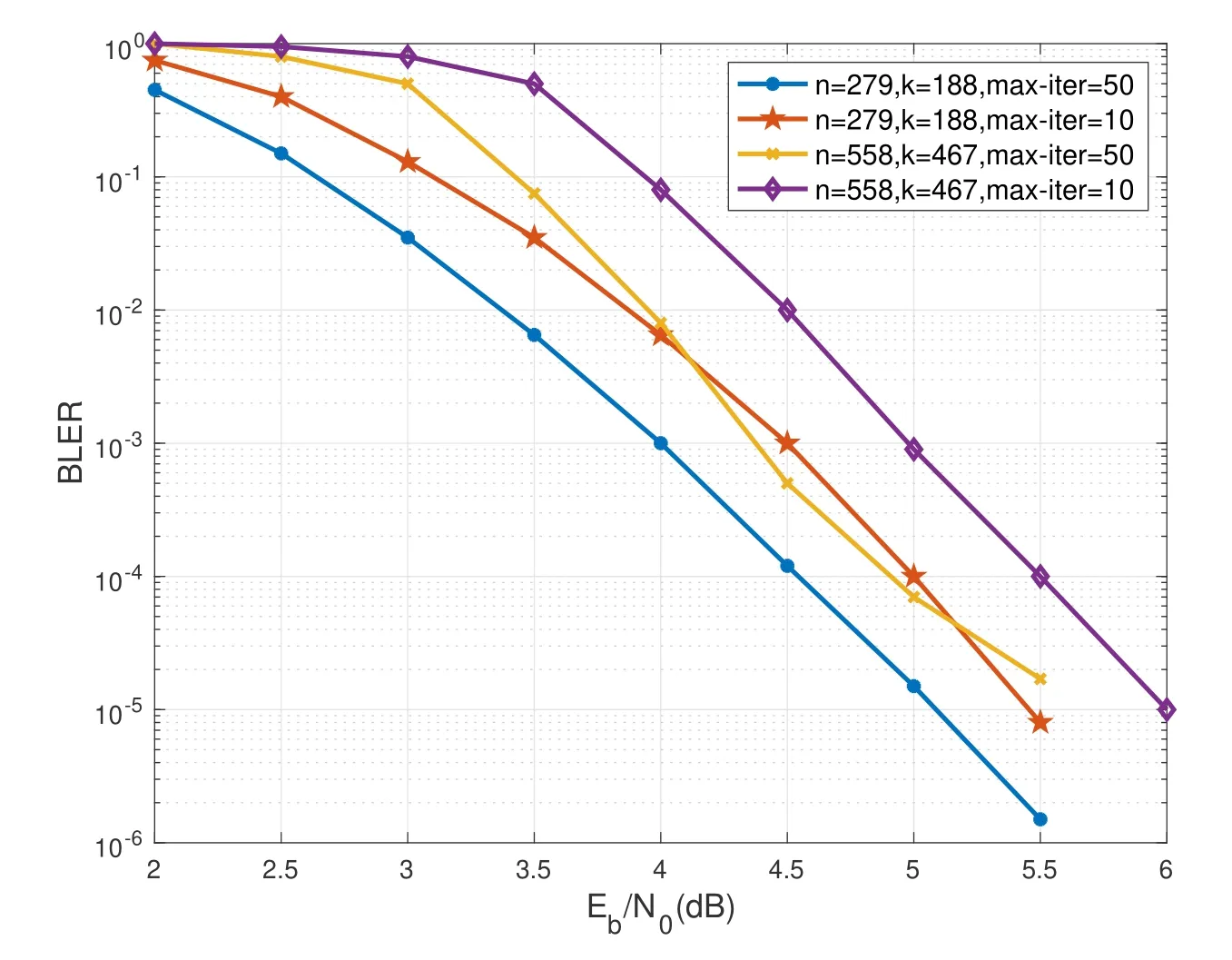
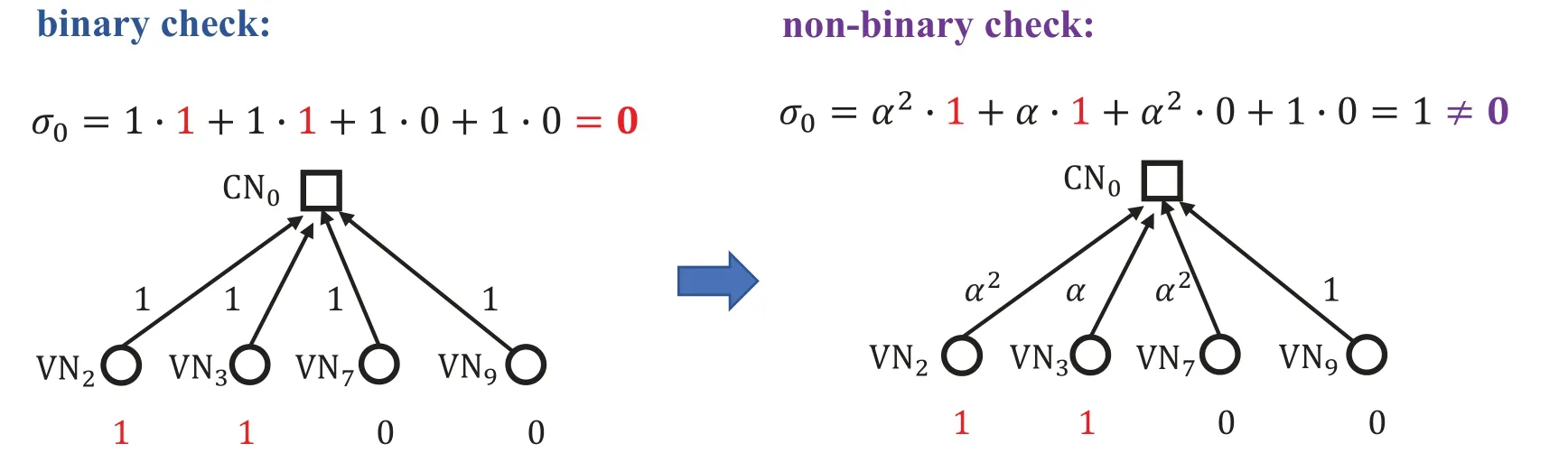
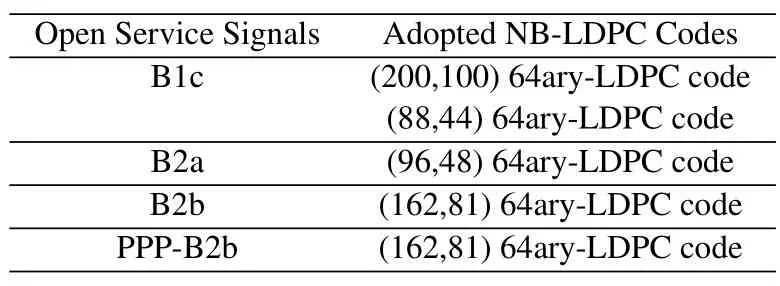
An(n,k)binary LDPC codeCcan be defined by the null space of anm×nbinary parity-check matrix H=[hi,j],where the rank of H is equal to(n ?k)≤m.The code length ofCisnand information length isk.The code rateRofCis equal toR=k/n.Define two index sets,Mj={i:0≤i An (n,k) binary LDPC codeCcan also be represented by a Tanner graph.It is a bipartite graph consisting of two types of nodes,variable nodes(VNs)andcheck nodes(CNs),and edges which connect a VN and a CN,respectively.Each VN in the Tanner graph ofCrepresents a column in the parity-check matrix H,and each CN represents a row in H.If thej-th VN,VNj,is connected to thei-th CN,CNi,by an edge,it means that the elementhi,jin H is ‘1’.The Tanner graph ofCcan be denoted byG=(V∪C,E),whereV={VN0,VN1,...,VNn?1} is the set of all VNs,C={CN0,CN1,...,CNm?1} is the set of all CNs,andEis the set of all edges connecting VNs and CNs.If the density of H is low,the value of|E|is a relatively small number andG=(V∪C,E)is sparse. Example 1.The parity-check matrix of a(12,3)regular binary LDPC code Cb with ρ=4and γ=3,respectively,is given as follows: The corresponding Tanner graph is shown in Figure 2. Let c=[c0,c1,...,cn?1] be one codeword of the(n,k) regular binary LDPC codeC.For 0≤j < n,each VNjcorresponds to a codeword bitcj.For each VNj,it indicates all hard-decision bitsci→jpassed from neighboring CNi,i ∈Mj,should be equal to the corresponding codeword bitcj,i.e., For example,the hard-decision bits passed to VN0of the(12,3)regular LDPC codeCbin Example 1 should fulfill Hence,the constraint in each VN of the regular LDPC codeCis equivalent to one(γ+1,1)repetition code(RPC). Figure 2.The Tanner graph of a(12,3)regular binary LDPC code Cb. For 0≤i < m,each CNidenotes a parity-check constraint equation of all codeword bits corresponding to neighboring VNs where the indexit ∈Ni,0≤t<ρ,and⊕is the XOR operation.For example,the parity-check constraint of CN0of the(12,3)regular LDPC codeCbshould fulfill Hence,the constraint in each CN of the regular LDPC codeCis equivalent to one (ρ,ρ ?1)single paritycheck code(SPC). The degree of each VN (respectively each CN) is equal to the number of edges connected to each VN(respectively each CN).Degree distribution polynomials usually are used to specify the degrees of VNs and CNs,respectively.Suppose the degree distribution polynomials of VNs and CNs areλ(x)=andrespectively,whereλdis the fraction of VNs with degreed,andρdis the fraction of CNs with degreed.The maximum degree of VNs (respectively CNs) isγmax(respectivelyρmax).For example,the degree distributions of VNs and CNs in Figure 2 areλ(x)=x2andρ(x)=x3,respectively. A sequence of edges forming a closed path in the Tanner graph is called a cycle.The number of edges which form the cycle is called the length of cycle.A cycle of lengthlis called cycle-l.The girth of a Tanner graph is defined as the length of its shortest cycle,denoted byg.The Tanner graph ofCbin Figure 2 does not have any cycle-4,but has cycle-6,one of which is indicated by the red edges.Thus,its girth isg=6. Based on the Tanner graph of LDPC codes,the MP decoding iteratively updates and passes reliability messages along the edges connecting VNs and CNs.The decoding process in each VN is called VN update,which computes the reliability message of each codeword bit and extrinsic reliability messages for each of neighboring CNs.The decoding processor in each CN is called CN update,which computes the extrinsic reliability messages for each of neighboring VNs. Consider the (n,k) regular binary LDPC codeCwith column weightγand row weightρ.Suppose a codeword c=(c0,c1,...,cn?1) ofCis transmitted over thebinary-input additive white-Gaussiannoise(BI-AWGN) channel withbinary phase shift keying(BPSK) modulation 0→+1 and 1→?1.The received vector is denoted by ann-tuple y=(y0,y1,...,yn?1).LetLj,0≤j < n,denote the input reliability message to VNjfrom the channel,andmjdenote the reliability message of the codewordcj.The extrinsic reliability messages passed from VNjto all neighboring CNs are defined asmj→i,i ∈Mj.The extrinsic reliability messages passed from CNi,0≤i < m,to all neighboring VNs are defined asui→j,j ∈Ni. For 0≤j whereσ2is the variance of the AWGN channel.The varianceσ2is equal to the two-sided power spectral densityN0/2 of the AWGN channel.Thus,it can be computed according to one of the measures of thesignal-to-noise-ratio(SNR),e.g.,the ratioEb/N0,whereEbis the average energy per information bit.Then,the reliability messagesmj→ipassed from VNjto all neighboring CNs are initialized asmj→i=Lj,i ∈Mj. Figure 3.An example of one VN update for the (12,3)LDPC code Cb in Example 1.Assume that all-zero codeword is transmitted. In VN update,each VNj,0≤j < n,updates the reliability messagemjof the codewordcjaccording to the constraint of the RPC in(1) and the extrinsic reliability messages for each of neighboring CNs wherei ∈Mj.Ifmj <0,the hard-decision bitof VNjis equal to 1; otherwise,=0.An example of one VN update for the (12,3) LDPC codeCbin Example 1 is shown in Figure 3. In CN update,each CNi,0≤i < m,computes the extrinsic reliability messages for each of neighboring VNs based on the constraint of SPC in(3) whereis the hyperbolic tangent function,and sgn(x) is the sign ofx.The iterative MP decoding algorithm using the above CN update is called thesum-product algorithm(SPA).An example of one CN update of the SPA for the(12,3)LDPC codeCbis shown in Figure 4. Figure 4.Examples of one CN update of the SPA and MS decoding for the (12,3) LDPC code Cb in Example 1.Assume that all-zero codeword is transmitted. The non-linear hyperbolic tangent function?(x)in CN updates is quite complex to implement.Thus,we usually approximate SPA by themin-sum(MS)decoding algorithm in hardware implementation.It replaces complex hyperbolic tangent operations by comparing and minimizing operations as follows: An example of one CN update of the MS algorithm for the(12,3)LDPC codeCbis shown in Figure 4.Besides its low complexity,it is more robust than the SPA for various channels.Thanks to minimizing operations of MS,the input reliability messages from BI-AWGN channel can be directly calculated without estimatingσas follows: By the cooperatively and iteratively work of the above VN and CN update,the reliability messages are passed to the full Tanner graph to achieve the global MP decoding.If the hard-decision vector=[,,...,] is a codeword,or the decoding exceeds the maximum iteration number,the decoding is terminated. It is worth mentioning that all VN and CN update units can be processed in parallel.In other words,the MP decoding can be decomposed into two layers of independent computation in VNs and CNs.As a result,the MP decoding owns highly parallel nature so that it is greatly suitable for high-speed transmission. Recently,many improved MP decoding algorithms have been proposed to achieve better trade-offs between decoding complexity and performance,such as thereliability-based iterative majority-logic decoding[31],thebelief-propagation-list erasure decoding[32],thethreshold-based MS decoding[33],and thediscrete MP decoding[34]. Figure 5.A partial graph of the(12,3)LDPC code Cb in Example 1 can be viewed as an approximate two-layer tree with the VN0 as the root node. On a cycle-free Tanner graph,the above iterative MP decoding can perform the exact MAP decoding for LDPC codes[7].It is because cycle-free Tanner graph can be regarded as a tree composed of VNs and CNs.Then,the iterative MP decoding can achieve a globally optimum solution through the locally operates on these nodes.However,cycle-free Tanner graphs generally can not support good codes whose minimum distance linearly increases with code length[35]. On a Tanner graph with cycles,the effectiveness of the iterative MP decoding is seriously affected by short cycles.Short cycles may highly likely force the decoder to continually work around a local loop,which will cause positive feedback too early and may result in decoding failure.However,as long as the probability of short cycles in a Tanner graph containing cycles is low,the MP decoder can also work well demonstrated by experimental results. Since high-density matrices inevitably have short cycles,e.g.,cycle-4,low-density matrices,i.e.,sparse Tanner graphs,are required for the MP decoding.In fact,constructions of good LDPC codes usually avoid short cycles,but not remove all the cycles in Tanner graphs of low-density matrices.Girthg ≥6 is important for obtaining satisfactory error performance. For example,a partial graph expanded from VN0of Tanner graph of girth 6 in Figure 2 can be viewed as an approximate two-layer tree with VN0as the root node,which is shown in Figure 5.If the third layer is expanded(check the blue edges),we will find a cycle-6 consisting of the red and blue edges. Besides short cycles,the performance of LDPC codes is influenced by the special undesirable structures in Tanner graphs,called trapping sets [15].Trapping sets mainly cause theerror-floor[36]phenomenon to LDPC codes with the MP decoding,i.e.,the slope of error-rate curve sharply slows at high SNR.It seriously limits the application of LDPC codes for low error-rate systems. An(a,b)trapping set is a setAofaVNs in a Tanner graphG=(V∪C,E)which induces a subgraphGt=(A∪Ct,Et) that containsbodd-degree CNs,whereCtis a set of all CNs adjacent to the VNs inA,andEtis the set of edges.LetBbe a set of all odd-degree CNs inCt,whereB ?Ctand|B|=b.Thus,an(a,b)trapping setAcan also be represented by(A,B). In general,trapping sets of smaller sizes are more harmful to error-floors,such as a (3,3) trapping set in the Tanner graph in Figure 2 as shown in Figure 6.Moreover,a class of special trapping sets,calledabsorbing sets[37],sometimes dominate the errorfloors.For an (a,b) absorbing set,most of CNs connected to the VNs have even degrees,i.e.,the value ofbis very small,e.g.,a(4,2)absorbing set in the Tanner graph in Figure 2 as shown in Figure 6. If the failure of one decoder is caused by trapping sets,this decoder may converge to an unchanged error state or oscillate among a set of error states during the decoding iterations.For example,the(4,2)absorbing set in Figure 6 can be resulted from flipping the bit of VN2outside the(3,3)trapping set in the Tanner graph of the (12,3) LDPC codeCb.Hence,it is necessary to consider the removing of small trapping sets from Tanner graph when constructing LDPC codes.Besides construction,post-processing techniques[38—40]have been introduced to break trapping sets based on the decoding results in case of the MP decoding failure. Figure 6.Several trapping sets in the Tanner graph of the (12,3) LDPC code Cb in Example 1.The filled squares are odd-degree CNs in the corresponding subgraphs. In order to remove short cycles and small trapping sets,several construction methods are proposed and investigated to design LDPC codes with good error performance.In this section,we first present the original pseudo-random design methods of Gallager and MacKay,respectively.Then,the PEG algorithm,an efficient computer search based construction,is reviewed.Last,we give algebraic constructions for QCLDPC codes.Moreover,EXIT chart can be used to optimize degree distributions to approach the channel capacity. A regular Gallager code has a parity-check matrix with uniform column weightγand row weightρ,both of which are very small compared to the code length.The parity-check matrix is divided intoγsubmatrices of sizeγ×n.Each submatrix is a regular matrix with row weightρa(bǔ)nd column weight 1.The first submatrix has the following specific form: thei-th row contains‘1’s in columnsiρto(i+1)ρ ?1,where 0≤i ≤γ ?1.The other submatrices are obtained by random column permutations of the first submatrix. A parity-check matrix of(12,3)Gallager codeCgis given as follows: The girth of Tanner graph ofCgis 4.For example,the red numbers in the above matrix form a cycle-4.Moreover,it has a large number of trapping sets. MacKay independently designed LDPC codes with sparse parity-check matrices.Moreover,he showed the ability of these codes to perform near channel capacity on thebinary-symmetric channel(BSC)and BIAWGN channel by computer simulation.One of the basic construction methods,proposed by Mackay,is that H is constructed by randomly generating uniform column weight and row weight as close to uniform as possible. The parity-check matrix of(12,3)Mackay codeCmis given as follows: Similar to Gallager codes,the design of Mackay codes can not guarantee the absence of cycle-4.The girth of Tanner graph ofCmis 4.A cycle-4 is indicated by the red numbers in the above matrix.It also has a large number of trapping sets. The PEG algorithm is a computer-based method for constructing Tanner graphs with locally maximized girth. In the construction process,each VN is connected to one edge at a time,called edge-by-edge manner.And the connection of edges starts with VNs with the lowest degree,and then progresses to VNs with increasing degree.Similarly,the edges connected to CNs begin with CNs with the lowest degree and the remaining edges are added to maximize the local girth.If CNs are not reachable from the current VN after traversing previously connected edges,connecting one of those CNs can form a larger cycle.Otherwise,choosing a CN with the lowest degree also can avoid short cycles.The construction method provides a fairly uniform degree distribution of CNs. In fact,the (12,3) LDPC codeCbin Example 1 is constructed by the PEG algorithm,which is a regular LDPC code.The partial construction process ofCbis shown in Figure 7.Without loss generality,some edges connected to VN0,VN1and VN2are omitted to simplify the graph.Considering VN3,the edge connected to CN2creates cycle-4,while the edge connected to CN1creates a larger local girth.The full Tanner graph without cycle-4 is shown in Figure 2. In addition,it is possible to use the variants of PEG algorithm,such as theapproximate cycle extrinsic message degree(ACE)algorithm[18],to avoid small trapping sets and result in lower error-floor. QC-LDPC codes are a class of structured LDPC codes,whose parity-check matrices consist of circulants.Thanks to their QC structure,QC-LDPC codes[20] can alleviate the wire routing problem for the MP decoding by simple shift registers and facilitate high-throughput design.Besides decoding,the QC structure promises efficient implementation of encoding process[41,42]. The parity-check matrix of a QC-LDPC code is an array of circulant matrices as follows where Ai,jis aZ ×Zcirculant matrix,0≤i < mband 0≤j < nb.Each row of Ai,jis a cyclic right shift (one place to the right) of its previous row,and the first row is the cyclic right shift of the last row.The first row of Ai,jis called the generator of Ai,j.If the generator of Ai,jis an all-zero vector,Ai,jis azero matrix(ZM).If a generator has only single nonzero element,the circulant matrix Ai,jis called thecirculant permutation matrix(CPM) [43].The array of circulant matrices brings regularity of parity-check matrices. QC-LDPC codes from CPMs and ZMs promise efficient memory access architecture in hardware implementation,which makes them the most popular LDPC codes in applications.They can be constructed by amatrix expansionprocess.The parity-check matrix H of sizembZ ×nbZis constructed through replacing each element in a relatively small well-designed matrix of sizemb × nb,i.e.,abase matrix,by a CPM or ZM of sizeZ × Z.One widely used expansion method is the(q ?1)-fold matrix expansion for a base matrix over a finite field GF(q),whereq=2r.The(q ?1)-fold matrix expansion of a non-zero elementαi ∈GF(q) is a (q ?1)×(q ?1) CPM over GF(2)whose generator has only single non-zero element‘1’at positioni,where 0≤i Figure 7.Construction process of the(12,3)LDPC code Cb in Example 1 based on the PEG algorithm. Example 2.Consider the field GF(q)and q=22.Let α be a primitive element of GF(22).The base matrixBof size4×4is over GF(22) On replacing each element inBby the3-fold matrix expansion,it obtains a4×4arrayHof3×3CPMs and ZMs over GF(2)as follows: The rank of the parity-checkHis equal to 8,and the null space ofHdefines a(12,4)QC-LDPC code.The Tanner graph of the (12,4) QC-LDPC code does not have any cycle-4. Recently,many powerful algebraic tools,such as finite geometries [8,44] and finite fields [10,11,45],have been used to design the RC-constrained arrays of CPMs.The RC constraint means no two rows (or two columns) in a matrix have more than one position in common that contains a non-zero element.The RC constraint can avoid cycle-4 in the Tanner graph.Well-designed algebraic QC-LDPC codes are capable of approaching the channel capacity with iterative MP decoding. ForFinite-geometry(FG)-QC-LDPC codes[8,44],many structural properties of finite geometries have been used for constructions,e.g.,the lines and points of Euclidean geometries and projective geometries.Forfinite-field(FF)-QC-LDPC codes[10,11,45],they are mainly constructed by the matrix expansion of elements in well-designed base matrices based on the basis of finite fields,e.g.,Latin Squares,the special codewords and parity-check matrices ofReed-Solomon(RS) codes,subgroups of a finite field and so on.In fact,the parity-check matrix H in Example 2 is constructed based on a Latin Square.It satisfies the RC constraint,and the girth of its Tanner graph is six. There are several works in deterministic analysis on QC-LDPC codes.In [43],Fossorier investigated the necessary and sufficient condition for QC-LDPC codes from CPMs to have a girth of 6,8,10,or 12.Recently,a matrix transformation approach is introduced to amicably investigate and study algebraic QCLDPC codes in the transform domain[46].Due to the block diagonal structure of their transformed paritycheck matrices,the ranks of the parity-check matrices of specific types of algebraic QC-LDPC codes can be determined. Figure 8.An EXIT chart for a rate-0.8 irregular LDPC code ensemble. In addition,QC-LDPC codes can be constructed by theprotograph-based(PTG-based) [47,48] method.It chooses a relatively small well-designed bipartite graph includingnbbase VNs andmbbase CNs,called base graph or protograph,for construction.Similar to base matrix,it can be defined by an adjacency matrix over integers.In an adjacency matrix,an entry greater than 1 indicates the presence of multi-parallel edges between corresponding base VN and CN in the protograph,the‘1’entry indicates the presence of an edge,and the‘0’entry indicates the absence of an edge. Similar to the matrix expansion,a large Tanner graph includingnbZVNs andmbZCNs of a PTGbased LDPC code can be constructed by agraph expansionprocess to the protograph.Graph expansion first generatesZcopies of the protograph,then permutes the edges of individual replicas among these copies.If the edges are permuted by cyclic permutations,the code will be QC.The expansion process of protograph sometimes is calledlifting,and the parameterZis calledlifting degree.The lifting usually involves computer-aided design,e.g.,using PEG or its variants,to avoid short cycles and small trapping sets.PTG-based QC-LDPC codes can achieve good error performance based on well-designed protographs and circulant permutations. An iterative decoding threshold is the theoretical performance limit of an ensemble of codes with given degree distributions as the code length and the number of iterations tend to infinity [10].Richardsonet al.[16] used density evolution to verify that degree distributions determine the thresholds of LDPC codes.It has been verified that it is possible to approach the limit by optimizing degree distributions.As an alternative method of density evolution,EXIT chart[19]is based on the Gaussian approximation,which has been widely applied. Since VNs and CNs for LDPC codes iteratively operate during decoding,EXIT chart can predict the decoding threshold of LDPC codes with given degree distributions by tracking themutual information(MI)exchanged between VNs and CNs.In fact,the transfer curves of VNs and CNs are averages of component EXIT curves weighed by the degree distributions.LetIA,VandIE,Vbe the input and output MI for VNs.The transfer function of VNs can be written as whereIE,V(d,IA,V) is given by [49].LetIA,CandIE,Cbe the input and output MI for CNs.The transfer function of CNs can be written as whereIE,C(d,IA,C) is given by [10].Based on the EXIT function of VNs and CNs,it is convenient to plot the transfer curves of VNs and CNs on the same axis,with the abscissa and ordinate reversed for CNs.By adjustingEb/N0,the initial touched point of the transfer curves of VNs and CNs (but not getting “stuck”)can be found,which indicates the decoding threshold with current degree distributions.To optimize the degree distributions,one has to find the set of degree distributions with the lowest decoding threshold(Eb/N0)EXIT. Figure 8 gives the EXIT chart analysis of a rateR=0.8 irregular LDPC code with three possible VN degrees,e.g.,2,3,8,and one CN degree,e.g.,19.The optimal degree distributions of VNs and CNs areλ(x)=0.2180x+0.3252x2+0.4567x7andρ(x)=x18,respectively,with threshold (Eb/N0)EXIT=2.3271 dB.Figure 8 shows the EXIT chart withEb/N0=3 dB.Because theEb/N0is above the threshold,we can see a pen tunnel between the two transfer curves. In addition,EXIT chart can be extended to analyze and design highly-structured capacity-approaching PTG-based LDPC codes [50].Later,it reveals that the convergence regions of PTG-based codes are governed by not only degree distributions,but also spatial coupling [51].The spatial coupling is to couple several individual LDPC codes together in a single chain,where the Tanner graph of each individual component is connected by the overlapped CNs.It can result in a new code ensemble,spatially coupled(SC)-LDPC ensemble [52],which is theLDPC convolutional code(LDPC-CC) ensemble [53] viewed from the spatial coupling point of view. Figure 9.The Tanner graph of a (3,1) block LDPC codeCbc. Example 3.Consider a (3,1) block LDPC code Cbc,whose parity-check matrixHbc is The corresponding Tanner graph of Cbc is shown in Figure 9. By coupling four identical block LDPC codes Cbc together in a single chain,it can result in a (12,4)SC-LDPC code Csc.The Tanner graph of Csc is shown in Figure 10,which is given by connecting the Tanner graph of each Cbc by one overlapped CN.The Tanner graph of Csc does not have any cycle-4. The corresponding parity-check matrixHsc of Csc is as follows: As described in[52],the spatial coupling of individual LDPC codes can increase the decoding threshold of the SC-LDPC ensemble to its maximum possible value.Thus,SC-LDPC codes have been a new way to approach channel capacity. Recently,several notable methods and EXIT chart analysis have been used to design SC-LDPC codes with good error performance [54—60].In [54],algebraic finite-length SC-LDPC codes based on replicateand-mask construction were proposed to have lower error-floors.In [56],two types of packings were derived based on balanced incomplete block designs to construct time-invariant SC-LDPC codes.In [58],optimized partitioning and lifting schemes were presented for constructing SC-LDPC codes with superior performance.In [59],multi-stage graph lifting process was introduced to construct SC-LDPC codes free of short cycles. Figure 10.The Tanner graph of a (12,4) SC-LDPC code Csc. Last,EXIT chart can also be used to design LDPC coded modulation [61],which is a powerful technique for using LDPC codes over practical channels.This technique is based on the concatenation of an LDPC encoder and a coded modulator for transmission over the given channel.For example,LDPC codes have been designed formultiple-input multipleoutput(MIMO) channels in [62].Moreover,the capacity-approaching performance has been demonstrated in some LDPC coded modulation schemes. In applications,coding gain is usually used to measure the performance of channel coding.It is defined as the reduction in theEb/N0required to achieve a specific error probability,e.g.,bit error-rate(BER),for a coded communication system compared to an uncoded system [10].Coding gain is obtained at only the expense of computational complexity of encoders and decoders.However,it brings substantial savings in overall system cost.For example,3dB coding gain means double of data transmission speed,reduction half of antenna area or double of covered area.Thus,modern communication systems tend to seek as large as possible coding gain. Moreover,in past decades,the transmission speed has been higher and higher.For instance,the peak download speed of 4G is 3 Gbps,but the peak download speed of 5G is up to 20 Gbps.Consider decoders usually occupy most resources in baseband chips.Modern communication systems tend to use codes whose decoders can be efficiently implemented with high-throughput. As mentioned in Section III,LDPC codes are not only capacity-approaching,but also can have very low error-floors in high SNR.They are capable to provide large coding gain.Moreover,their MP decoders have low complexity and parallel nature.They can be implemented in highly parallel architecture.Last,the introduction of the QC structure promises efficient wire-routing and memory access.As a result,QC-LDPC codes are the most popular capacityapproaching codes for high-speed communication systems over the past two decades.Now we would like to present their success in the following typical communication systems,Landsat satellites,Chang’e Chinese lunar mission and 5G mobile communications. Landsat is a long-term land remote sensing satellite program,which contains theLandsat Data Continuity Mission(LDCM),also known as Landsat 8,to obtain satellite imagery of earth.Its satellite data and imagery are the main source of Google Earth Engine,and the key foundation for the recently released Google Earth 3D Timelapse tool.LDCM requires 384 Mbps data rate communication at the 375 MHz X-band,which is significantly higher than previous Landsat missions.Moreover,the required BER is as low as 10?12to support theConsultative Committee on Space Data Systems(CCSDS) file delivery protocol system.Convolutional codes and RS codes have been used extensively and very successfully on many NASA missions,such as the Hubble Space Telescope,Voyager and Galileo.However,the code rate of combination of RS and convolutional codes isR=0.43,requiring a symbol transmission rate of 880 Msps.The main lobe needs 880 MHz withquadrature phase shift keying(QPSK)modulation,considering the two-sided power spectrum.It is difficult to fit into the 375 MHz X-band[63]. Compared to the combination of RS and convolutional codes,the (8176,7156) QC-LDPC codeCqcwithR=7/8,designed by Linet al.in 2004 [21],has been used in LDCM.The parity-check matrix HqcofCqcwith row weightρ=32 and column weightγ=4 is where Ai,jis a 511×511 circulant matrix,0≤i<1 and 0≤j <15.The generator of Ai,jhas two nonzero elements.Its Tanner graph has girth at least 6.Since the code rate isR=7/8,the main lobe occupies 440 MHz with QPSK modulation.It can be filtered to fit the 375 MHz X-band.In fact,the 384 Mbps data rate communications link is the first time NASA has used LDPC codes,and the first time any agency or company has used LDPC codes for a space to ground link. Moreover,the mission requirement for BER of 10?12is met by this code.And the convergence rates allow for real time decoding for imaging missions[63].The error performance of the(8176,7156)QCLDPC code [64],using BPSK modulation,with the SPA and MS decoding is given in Figure 11.It shows the waterfall performance of this code and no observations of error-floor down to the BER of 10?14,which meets the required BER.The high coding gain also allows for better land-cover characterization. Now LDPC codes have been widely used in NASA missions.For instance,the rate-7/8 LDPC code has also been used in Geostationary Operational Environmental Satellite.Theaccumulate-repeat-4-jaggedaccumulate(AR4A) LDPC codes [65],constructed from the PTG-based LDPC codes,have been used in deep-spaces applications. In Chang’e lunar exploration mission,one of the major technical challenges is the transmission capability of the long-rangetelemetry,tracking,and command(TT&C)system to monitor the unmanned probe in lunar orbit.In fact,since the distance between the Moon and the earth exceeds 400,000 kilometers and the antenna aperture is restricted,transmitted signals will suffer from large path attenuation and severe bursty interference in space electromagnetic environment.LDPC codes with outstanding error-correcting capability are good candidates to guarantee transmission quality of the TT&C system.However,compared with traditional channel coding schemes,the implementation complexity of LDPC codes is notably higher due to their sparse random construction.Thus,efforts should be paid to the new design of LDPC codes that can be implemented on resource-restricted space hardware platforms. A semi-random code design strategy is introduced to construct structured LDPC codes with better trade-offs between performance and complexity [66].Specifically,by exploiting the structure of Hamiltonian cage graph,a base matrix is firstly obtained with constrained minimum distance and girth [67].Then,the parity-check matrix H will be established by expanding the base matrix with different types of submatrices.For example,the constructed (2032,1016)LDPC code can be expressed by where E127denotes a 127×127 dual-diagonal submatrix,and A1,016×1,016is expanded from a 8×8 base matrix Ab.Each zero element of Abis extended to a 127×127 all-zero matrix,while each one element is extended to a 127×127 pseudo-random permutation matrix.Note that the permutation matrix will be generated by a two-dimensional structure in Galois field,which brings in more than 100 times of structure freedom than the conventional cyclic identity matrix.Detailed expanding process can be referred to[68]. Performance of the structured LDPC code is further evaluated by numerical simulations.As shown in Figure 12,the structured LDPC code outperforms the traditional rate-1/2 convolutional code by increasing the coding gain by 2.5 dB,indicating nearly half of transmission power can be saved.Meanwhile,it is able to well meet the restricted engineering constraints of deep space applications,and has been successfully applied to the mission of Chang’e lunar exploration.Moreover,based on the structure of Hamiltonian cage graph,high-dimensional algebraic code constraints can be employed to construct low-rate generalized sparse codes [69],which is able to provide ultra-reliable and efficient transmission capability for application scenarios with harsh communication channels,such as helicopter-satellite communication [70],ultra-reliable and low latency communications(URLLC)[71],andquantum-secure direct communications(QSDC)[72]. Figure 11.BER performance of the(8176,7156)QC-LDPC code with the SPA and MS decoding respectively.The maximum number of iterations is 50. 5GNew Radio(NR) requires channel coding to satisfy the broad requirements,such as highthroughput,low-latency,high-reliability,supporting forincremental-redundancy hybrid automatic repeatrequest(IR-HARQ),and flexible block-lengths and coding rates.In 2016,three well-known channel capacity-approaching codes,LDPC,Turbo,and polar codes,were considered as candidates of the eMBB data channel coding schemes.The chairman’s notes of Agenda Item 8.1.3 in 3GPP TSG RAN WG1 Meeting #86bis [22] summarized the proposed observations of channel coding schemes from Huawei,Qualcomm,Ericsson,Sumsung and so on,as follows, ■LDPC codes:They are proven,mature and capable,at least when focusing on achieving highthroughput.LDPC codes can deliver acceptableblock error-rate(BLER),throughput,latency,areaefficiency and energy-efficiency for NR,at least at medium to high coding rates. ■Turbo codes:They are proven,mature and capable,at least when focusing on achieving flexibility and HARQ.TheLong Term Evolution(LTE)Turbo code and enhanced LTE Turbo codes can deliver acceptable BLER,flexibility,HARQ,latency,areaefficiency and energy-efficiency for NR,at least at medium to low coding rates.Turbo codes will be a necessary part of NR devices supporting nonstandalone operation and/or legacy LTE connectivity. ■Polar codes:They are less mature,at least for larger list sizes.Polar codes require list decoding to meet the BLER requirements of NR,which degrades the throughput,latency,area-efficiency and energy-efficiency of polar decoders. Figure 12.BER Performance of the proposed structured LDPC code by using BPSK modulation over the AWGN channel,where the SPA decoding with a maximum number of iterations of 32 is adopted. In short,LDPC codes can efficiently support the whole range of eMBB data channel rates,blocklengths,and IR-HARQ with fine granularity.They can provide better area-efficiency and energy-efficiency than the other coding schemes,especially for highthroughput.They are amenable to parallelization and can provide better decoding latency.Moreover,they can support the peak data download rate of 20 Gbps for eMBB.Finally,LDPC codes have been adopted as the eMBB channel coding scheme of high-speed data transmission in eMBB of 5G. 5G NR QC-LDPC codes in 3GPP are constructed based on the structured graphs,i.e.,their Tanner graphs can be obtained by lifting a base graph which does not have multiple edges between a base VN and CN.Two typically specified rate-compatible base graphs,called BG1 and BG2,respectively,have been considered for 5G NR QC-LDPC codes[73,74].BG1 is the main 5G NR high-rate base graph,and BG2 is the low-rate base graph. Figure 13.Sketch of the adjacency matrix of base graph structure adopted for the 5G NR QC-LDPC code. The adjacency matrices of BG1 and BG2 have similar structures,and the sketch of the adjacency matrices is shown in Figure 13.The matrix A in Figure 13 corresponds to the information columns of lengthkb,B is a block dual-diagonal matrix which corresponds to the core parity columns,O is a ZM,E is a sparse matrix which corresponds to extension checks,and I is an identity matrix.The maximum values ofkbfor BG1 and BG2 are 22 and 10,respectively.By puncturing or shortening,BG1 and BG2 can meet a wide range of block-lengths and code rates. BG1 and BG2 support various values of the lifting degreeZ.The maximum number ofZis 384,and many smaller values ofZfulfillingZ=a·2jare also supported,wherea={2,3,5,7,9,11,13,15} and 0≤j ≤7.The range of information lengthsksupported by BG1(respectively BG2)is from 308 to 8448(respectively 40 to 3840),and the range of code rates supported by BG1 (respectively BG2) is from 1/3 to 11/12(respectively 1/5 to 2/3)[75]. Example 4.The error performance of various 5G NR LDPC codes,using BPSK modulation,with various code lengths and maximum iterations is given as follows[76]: For URLLC of 5G,it requires strong data channel coding schemes with short block-lengths to satisfy two requirements of ultra-low latency and ultra-high reliability.5G NR QC-LDPC codes based on BG2 have also been considered for URLLC data channel[77]. Recently,constructions and improvements for short block-length LDPC codes,especially for a few hundreds bits,with better performance have been further studied.In [78],raptor-like protograph codes with short block-lengths were constructed by a simplified error minimization PEG algorithm with protograph optimization.In[79],a technique for constructing rate compatible LDPC codes by extending a protograph was introduced to obtain lower error floors at short block-lengths.In [80],an upper bound on the minimum distance was used as a potential metric for short block-length code design. In this section,we will present NB-LDPC codes,which are viewed as the extension of binary LDPC codes.NB-LDPC codes,especially for short and moderate code lengths,have been demonstrated to have higher coding gains,lower error-floors,and more suitable for high order modulation than their binary counterparts over a wide range of channels.However,the complexity of their MP decoding is too higher for practical applications.Recently,a variety of low complexity MP decoding algorithms have been proposed.Thus,NB-LDPC codes have become attractive for low/moderate speed data transmission.For instance,they have been applied in the navigation message design of BeiDou navigation system to improve the error performance under harsh environment. NB-LDPC codes[23]over Galois fields GF(q)of orderq=pr(pis a prime andr >1),are also known asq-ary LDPC codes.Letαbe a primitive element of a Galois field GF(q),andαican be used to represent all elements which belong to GF(q),wherei ∈{0,1,...,q ?2,?∞}andα?∞?0.Forq=2r,each element over GF(2r)can be further mapped into a unique binary tuple of lengthror a unique binary image matrix of sizer×r.Thus,each symbol in NBLDPC codes over GF(2r)can be represented by field elementsαi,i ∈{0,1,...,q ?2,?∞},orrbinary bits. An NB-LDPC code over GF(q)is defined by a very sparse parity-check matrix over GF(q) (q >2).The non-zero entries in its parity-check matrix belong toq?1 non-zero field elementsαi,i ∈{0,1,...,q?2},rather than only ‘1’s of binary LDPC codes.For an(n,k)q-ary LDPC codeC,it is defined by the null space of anm×nparity-check matrix H=[hi,j]over GF(q),where each coefficienthi,jbelongs to GF(q). Ifhi,j≠0,thei-th CN,CNi,in the Tanner graph of NB-LDPC codeCis connected to thej-th VN,VNj,by an edge.Suppose c=[c0,c1,...,cn?1]is a codeword of the NB-LDPC codeC.Each VNjin the Tanner graph of the NB-LDPC codeCcorresponds to each codeword symbolcjover GF(q),0≤j < n.The parity-check constraint equation in each CN is based on the symbols over GF(q)rather than binary bits.The reliability messages passed from VNjto CNialong the edge are respectively permuted by the coefficienthi,jover GF(q),i.e.,multiplied byhi,j; while reliability messages passed from CNito VNjwill be inversely permuted byhi,j,i.e.,multiplied by the inverse element ofhi,j. Example 5.The parity-check matrixHnb of a(12,3)regular LDPC code Cnb over GF(22)with row weight ρ=4and column weight γ=3is given as follows: where α is a primitive of GF(22).The positions of non-zero elements inHnb are the same as the binary parity-check matrixHb in Example 1,while the nonzero elements inHnb are symbols over GF(22)rather than only ‘1’.The Tanner graph of Cnb has the samestructure of the Tanner graph of the binary LDPC code Cb in Figure 2,while each edge in the Tanner graph of Cnb corresponds to a non-zero coefficient over GF(22)inHnb. Figure 14.The error performance of various 5G NR LDPC codes with the SPA decoding.The code lengths are n=279 and n=558,respectively.The maximum iterations(max-iter)are 50 and 10,respectively. Examples of the parity-check constraints of CN0for the (12,3) NB-LDPC code Cnb over GF(22)and the(12,3)binary LDPC code Cb are shown in Figure 15.The check sum of CN0over GF(22)is equal to a nonzero element,thus errors in VN2and VN3can be detected.However,for the same number of errors,the check sum of binary CN0is equal to zero which can not detect errors.In other words,the CN0of NB-LDPC code Cnb is more resistant to errors than the CN0of binary LDPC code Cb. Since symbols in aq-ary LDPC code are over GF(q),the messages propagated along edges connected VNs and CNs are the symbol probability vectors of lengthqor their corresponding LLR vectors.The optimal MP decoding algorithm for NB-LDPC codes is theqary sum-product algorithm(QSPA) which stores and computes theq-vector reliability messages. Let U0,U1,...,Uρ?1be the input probability vectors of lengthqentering a CN of degreeρ,and V0,V1,...,Vρ?1be the output probability vectors of lengthqfor this CN.Assume that U0,U1,...,Uρ?1have been respectively permuted by the corresponding coefficients in the parity-check matrix.Letai,0≤i < q,be an arbitrary element in GF(q).Thei-th element in the probability vector represents the probability value of the field elementai,for 0≤i The update of this CN for QSPA is a convolution of probability vectors over GF(q) where?is the vector convolution operation.Thei-th elementVj[i]in Vjis computed by where 0≤i Thus,the computation complexity of CN update of QSPA isO(ρq2).Even if the fast decoding of QSPA based on afast Fourier transform(FFT) can reduce the computation complexity of CN update intoO(ρqlog2q) for NB-LDPC codes over GF(q),it still is quite complex to implement. Figure 15.Examples of the parity-check constraints of CN0 for the(12,3)NB-LDPC code Cnb over GF(22)and the(12,3)binary LDPC code Cb.Assume that all-zero codeword is transmitted,and there are two errors in VN2 and VN3.The‘+’in binary check and non-binary check represents the sum operation over GF(2)and GF(22),respectively. So far,many sub-optimal MP decoding algorithms have been presented to simplify the CN update for NBLDPC codes,such as theExtended MS(EMS) [24]decoding algorithm,thetrellis based EMS(T-EMS)[26]decoding algorithm,and their modified versions.By only storing and computing thenmmost reliable messages (nm ?q) among theqelements,the EMS decoding algorithm reduces the computational complexity of per CN update toO(ρnmlog2nm).The TEMS decoding algorithm only computes the deviation paths which differ from the most reliable path in at mostncdeviation nodes (nc ?q) selected fromnr(nr ?q)most reliable nodes in each row of one trellis of per CN.The computational complexity of per CN update of T-EMS is reduced toO(nrn2c).However,as the complexity decreases,the error performance of the above sub-optimal MP decoding algorithms may suffer significant performance loss. Recently,Huang and Songet al.[28] have introduced set partition to partition elements in one trellis of per CN into different sets according to their different contributions to error performance.It has been proven that the deviation paths constructed from the most reliable sets of the trellis locate in several fixed positions.The proposedFix-path MS(FMS)decoding algorithm [28] only requires to calculate these fixed paths,and does not require to search the deviation paths over the whole trellis of a CN.Thus,the com-putational complexity of real operations for per CN update can be reduced toO(ρ).The FMS algorithm can efficiently decode NB-LDPC codes of low/moderate code rates,including ultra-sparse ones. Table 1.Code parameters of NB-LDPC codes used in the open service signals of BeiDou navigation system. BeiDou navigation is a global satellite navigation system,where navigation message usually is transmitted at low speed.Due to the long transmission distance and partial spectrum overlap,there are many errors in navigation messages whose lengths range from about dozens to 1800 bits in BeiDou navigation system.Under these code lengths,NB-LDPC codes outperform their binary counterparts up to about 1 dB.Moreover,the efficient decoding,e.g.,FMS,can significantly facilitate their low-throughput implementation.As a result,the global BeiDou navigation system mainly adopts the 64-ary LDPC codes of 1/2 code rates with various code lengths for the navigation messages of various open service signals[29,30],which are summarized in Table 1. It has been demonstrated that well-designed LDPC codes can approach channel capacity by the MP decoding with linear complexity and highly parallel nature.Moreover,thanks to the introduction of the QC structure,their decoders and encoders can be implemented with high area-efficiency and energyefficiency.Thus,it makes LDPC codes the most attractive highway to approach channel capacity.In fact,QC-LDPC codes have become the most popular coding for high-speed communications. ACKONWLEDGEMENT The authors would like to sincerely thank Prof.Liuguo Yin for the contribution to this paper.They thank Prof.Zesong Fei,Haiyang Liu,Shancheng Zhao and Chuan Zhang for their valuable comments and constructive suggestions.They also thank Dr.Yuejun Wei for helpful suggestions on standards. The work was supported in part by the National Natural Science Foundation of China(No.62071026,No.62201152 and No.61941106),the Natural Science Foundation of Fujian Province(No.2021J05034),and Key Project of Science and Technology Innovation of Fujian Province (No.2021G02006).(Liyuan Song and Shuyan Yu contributed equally to this work.)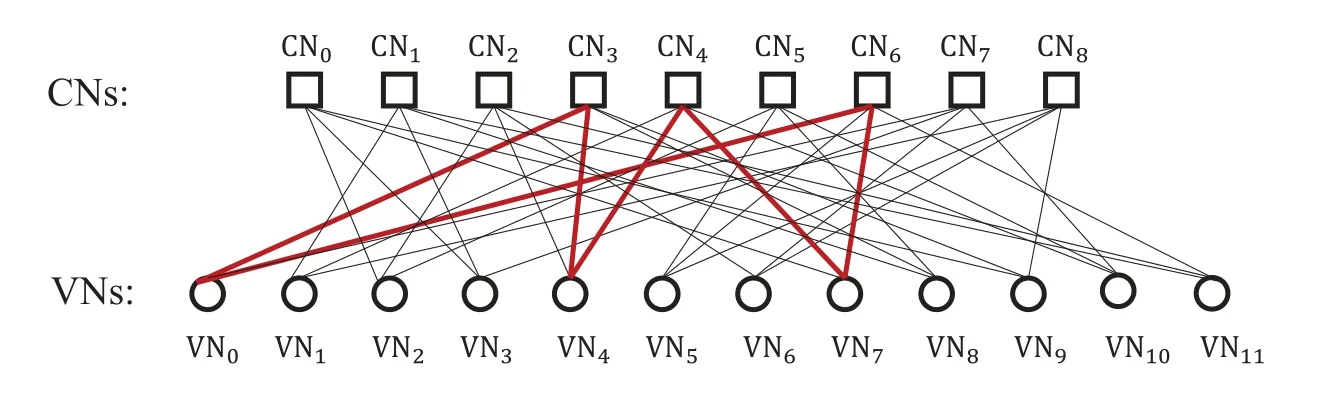
2.2 MP Decoding for LDPC Codes
2.3 Cycle-Free Tanner Graphs
2.4 Trapping Sets

III.CONSTRUCTION OF LDPC CODES
3.1 Gallager Codes
3.2 MacKay Codes
3.3 PEG Codes
3.4 QC-LDPC Codes
3.5 EXIT Chart
IV.APPLICATION FOR COMMUNICATIONS
4.1 Landsat Satellites
4.2 Chang’e Chinese Lunar Mission
4.3 5G LDPC Codes
V.NB-LDPC CODES
5.1 Definition of NB-LDPC Codes
5.2 MP Decoding for NB-LDPC Codes
5.3 Application for BeiDou Navigation System
VI.CONCLUSION

