王 鵬, 唐孝敏

(黑龍江大學(xué) 數(shù)學(xué)科學(xué)學(xué)院, 哈爾濱 150080)

0 引 言

局部導(dǎo)子[1]可視為導(dǎo)子的一種推廣, 關(guān)于李代數(shù)局部導(dǎo)子問(wèn)題的研究主要是判斷其局部導(dǎo)子是否為導(dǎo)子[2-4].自由粒子Schr?dinger方程的對(duì)稱(chēng)群為Schr?dinger李群, 其對(duì)應(yīng)(n+1)-維時(shí)空的李代數(shù)稱(chēng)為Schr?dinger代數(shù)[5].Schr?dinger代數(shù)是一類(lèi)重要的非半單李代數(shù), 在量子物理中應(yīng)用廣泛.文獻(xiàn)[6-10]研究了(1+1)-維時(shí)空的Schr?dinger代數(shù)的結(jié)構(gòu)與表示理論.本文考慮(1+1)-維時(shí)空的Schr?dinger代數(shù)S, 給出其局部導(dǎo)子的結(jié)構(gòu).

Schr?dinger代數(shù)S是一個(gè)復(fù)李代數(shù), 具有基{e,f,g,h,l,z}, 其基之間的非平凡李積如下:

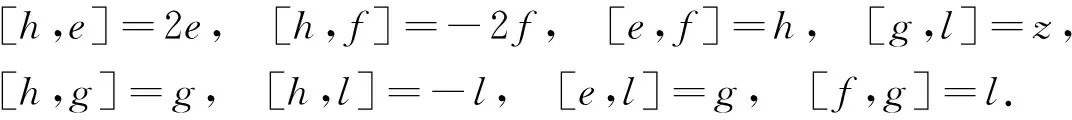
(1)

1 預(yù)備知識(shí)

本文約定L是一個(gè)李代數(shù).

定義1若D滿(mǎn)足

D([x,y])=[D(x),y]+[x,D(y)], ?x,y∈L,

則L上的線(xiàn)性變換D稱(chēng)為L(zhǎng)的導(dǎo)子.

記所有L的導(dǎo)子構(gòu)成的集合為Der(L).易證Der(L)是一個(gè)向量空間.對(duì)于L中的任意向量x, 易驗(yàn)證L上的線(xiàn)性變換adx: adx(y)=[x,y](?y∈L)是L的導(dǎo)子, 稱(chēng)為L(zhǎng)的內(nèi)導(dǎo)子.記L所有內(nèi)導(dǎo)子構(gòu)成的集合為Ider(L).易證Ider(L)是一個(gè)向量空間.

定義2設(shè)Δ是L上的一個(gè)線(xiàn)性變換, 若對(duì)任意的x∈L, 均存在L的一個(gè)導(dǎo)子D(x), 使得Δ(x)=D(x)(x), 則稱(chēng)Δ是L的一個(gè)局部導(dǎo)子.

記L所有局部導(dǎo)子構(gòu)成的集合為L(zhǎng)der(L).易證Lder(L)是一個(gè)向量空間, 且Der(L)是Lder(L)的子空間.

引理1[6]Der(S)=Ider(S)⊕σ, 其中σ是S的一個(gè)外導(dǎo)子且滿(mǎn)足如下關(guān)系:

注意到adz=0, 由引理1易得如下引理:

引理2Der(S )=Span{ade,adf,adg,adh,adl,σ}.

2 主要結(jié)果

設(shè)Δ是Schr?dinger代數(shù)S的一個(gè)局部導(dǎo)子, 對(duì)于S中的基元l, 由局部導(dǎo)子的定義知: 存在D(l)∈Der(S), 使得Δ(l)=D(l)(l).令Δ1=Δ-D(l), 易見(jiàn)Δ1∈Lder(S)且滿(mǎn)足Δ1(l)=0.下面仍用Δ記Δ1.不妨設(shè)Δ∈Lder(S)且滿(mǎn)足Δ(l)=0.設(shè)Δ(e),Δ(f),Δ(g),Δ(h),Δ(z)在基e,f,g,h,l,z下的表示矩陣為AΔ=(aij)6×5, 即有

(Δ(e)Δ(f)Δ(g)Δ(h)Δ(z))=(efghlz)AΔ.

(2)

任取x∈S{0}, 總設(shè)

其中xe,xf,xg,xh,xl,xz∈.又設(shè)使得

(σ(x) ade(x) adf(x) adg(x) adh(x) adl(x))=(efghlz)Bx.

(4)

對(duì)式(4)結(jié)合式(1)和式(3), 計(jì)算可得

(5)

對(duì)于上述x, 由局部導(dǎo)子的定義知, 存在導(dǎo)子D(x)使得Δ(x)=D(x)(x).由引理2,D(x)可表達(dá)為

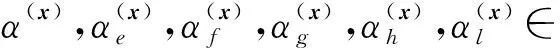
(7)

從而有

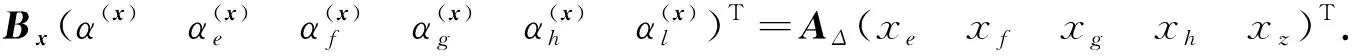
(8)

結(jié)合式(5), 記

(9)

其中

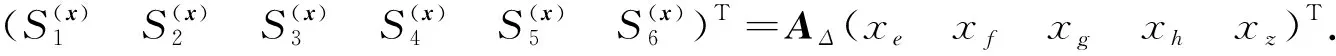
由式(8)及線(xiàn)性方程組有解的判定定理易得如下引理:

引理3令Δ是S上的一個(gè)線(xiàn)性變換, 且滿(mǎn)足Δ(l)=0, 則對(duì)于任意由式(3)給出的x,Δ∈Lder(S)的充分必要條件是

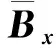
下面計(jì)算AΔ.

引理4如果Δ∈Lder(S)且Δ(l)=0, 則AΔ具有以下形式:

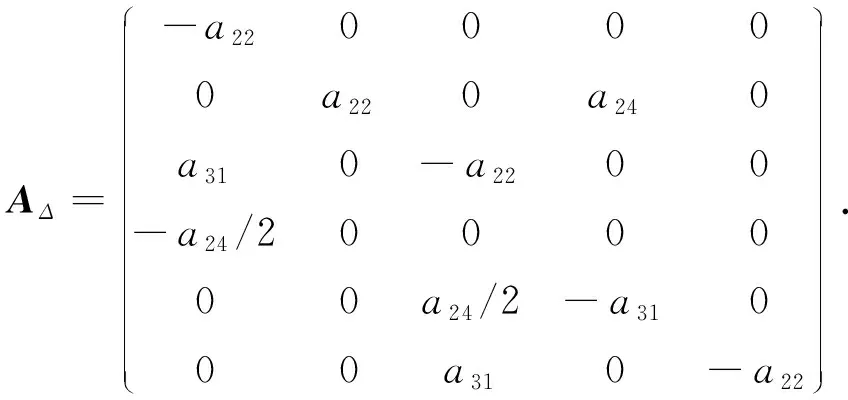
(10)

證明: 證明分為如下四步.

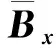
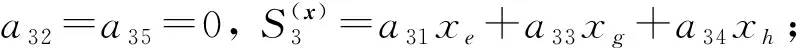
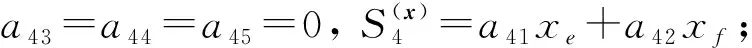
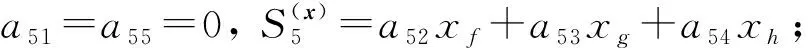
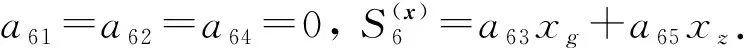
綜上, 有

2) 若在引理3中取x滿(mǎn)足xe=0,xh≠0, 則由式(9)有

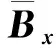
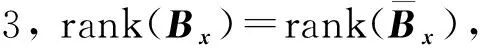
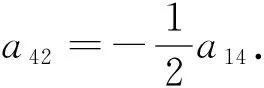
(11)

若在引理3中取x滿(mǎn)足xf=0,xh≠0, 則由式(9)有

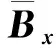
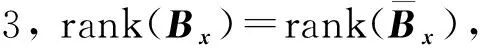
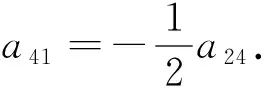
(12)

根據(jù)1)的結(jié)果以及式(11),(12)有

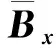
a11=-a22.

(13)

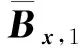
取x滿(mǎn)足

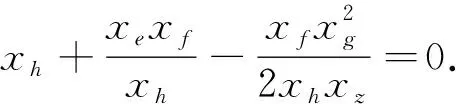
(14)

再根據(jù)引理3和2)的結(jié)果有

首先, 在式(15)中取xe=0, 可得

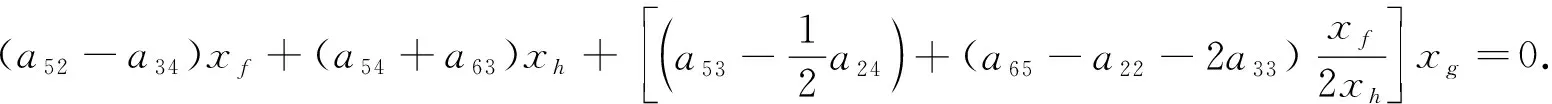
(16)

在式(16)中分別取xg=1和xg=2, 有

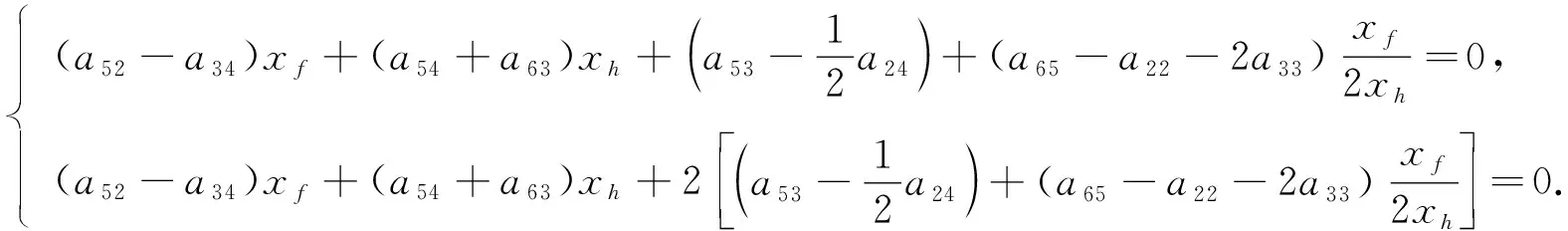
(17)

由式(17)有

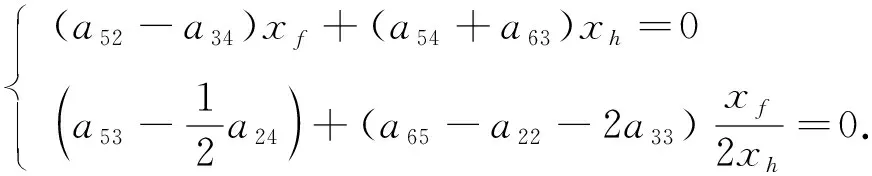
(18)

在式(18)中取xh=1并分別取xf=1和xf=2, 經(jīng)計(jì)算可得

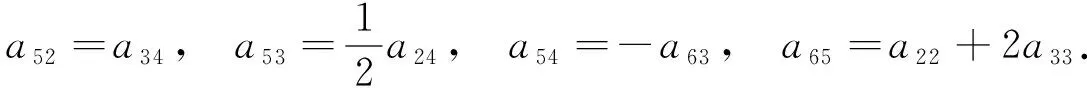
(19)

其次, 由式(14)知, 若xf=0, 則xh=0.因此取xh≠0即有xf≠0.于是由式(15)和式(19)知, (a63-a31)xe=0.再取xe≠0可得

a63=a31.

(20)

結(jié)合式(13),(19),(20)和2)的結(jié)果知

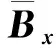
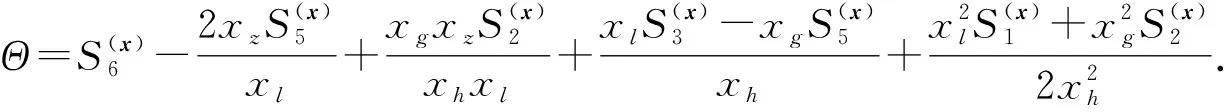
當(dāng)x的系數(shù)滿(mǎn)足xgxl+xhxz=0時(shí), 由引理3和3)的結(jié)果知

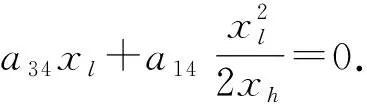
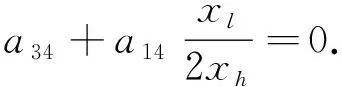
(22)

在式(22)中取xh=1, 并分別取xl=1和xl=2易得

a34=a14=0.

(23)

結(jié)合式(21)和式(23)可得(a22+a33)xz=0.進(jìn)而取xz≠0可知

a33=-a22.

(24)

最后, 結(jié)合式(23),(24)和3)的結(jié)果知AΔ具有式(10)的形式.證畢.

定理1Schr?dinger代數(shù)S的每個(gè)局部導(dǎo)子都是導(dǎo)子, 即Lder(S)=Der(S).

證明: 設(shè)Δ°是Schr?dinger代數(shù)S的一個(gè)局部導(dǎo)子, 則由局部導(dǎo)子的定義知, 存在D(l)∈Der(S), 使得Δ°(l)=D(l)(l).令Δ=Δ°-D(l)∈Lder(S), 則有Δ(l)=0.

根據(jù)式(1)～(3)和引理4, 有

因此,

于是有Δ°=Δ+D(l)∈Der(S), 故Lder(S)?Der(S).顯然又有Lder(S)?Der(S), 所以L(fǎng)der(S)=Der(S).證畢.