Finite Abelian Groups of K3 Surfaces with Smooth Quotient
Taro HAYASHI
Abstract The quotient space of a K3 surface by a finite group is an Enriques surface or a rational surface if it is smooth.Finite groups where the quotient space are Enriques surfaces are known.In this paper, by analyzing effective divisors on smooth rational surfaces, the author will study finite groups which act faithfully on K3 surfaces such that the quotient space are smooth.In particular,he will completely determine effective divisors on Hirzebruch surfaces such that there is a finite Abelian cover from a K3 surface to a Hirzebrunch surface such that the branch divisor is that effective divisor.Furthermore,he will decide the Galois group and give the way to construct that Abelian cover from an effective divisor on a Hirzebruch surface.Subsequently, he studies the same theme for Enriques surfaces.
Keywords K3 surface, Finite Abelian group, Abelian cover of a smooth rational surface
1 Introduction
In this paper, we work over C.AK3 surfaceXis a smooth surface withh1(OX) = 0 and OX(KX)OX, whereKXis the canonical divisor ofX.In particular, aK3 surface is simply connected.Finite groups acting faithfully onK3 surfaces are well studied.Letωbe a nondegenerated two holomorphic form.An automorphismfof aK3 surface is called symplectic iff?ω=ω.A finite subgroupGof automorphisms of aK3 surface is called symplectic ifGis generated by symplectic automorphisms.The minimal resolutionXmof the quotient spaceX/Gis one of aK3 surface, an Enriques surface and a rational surface.The surfaceXmis aK3 surface if and only ifGis a symplectic group.Symplectic groups are classified (see [10,13, 16]).If the quotient space ofX/Gis smooth, then it is an Enriques surface or a rational surface.The quotient spaceX/Gis an Enriques surface if and only ifGis isomorphic to Z/2Z as a group and the fixed locus ofGis an empty set.It is not well-known what kind of rational surface is realized as the quotient space of aK3 surface by a finite subgroup of Aut(X).In this paper, we will consider the case whereX/Gis a smooth rational surface.The minimal model of smooth rational surfaces is the projective plane P2or a Hirzebruch surfaces Fnwheren≠1,and F1is isomorphic to P2blow-up at a point.In other words, all smooth rational surfaces which are not minimal are F1or given by blowups of Fnfor 0 ≤n.Therefore, ifX/Gis not P2, then there is a birational morphismf:X/G→Fn.Our first main results are to analyze the quotient spaceX/GandGwhenX/Gis smooth.
Theorem 1.1Let X be a K3surface and G be a finite subgroup ofAut(X)such that X/G is smooth.For a birational morphism f:X/G→Fnfrom the quotient space X/G to a Hirzebruch surfaceFn, we get that n=0,1,2,3,4,6,8or12.Furthermore, if n=6,8,12, then f is an isomorphism.
LetXbe aK3 surface, andωbe a non-degenerated holomorphic two form ofX.For a finite groupGof Aut(X), we writeGsas a set of symplectic automorphisms ofG.Then there is a short exact sequence: 1 →Gs→GCn→1, whereCnis a cyclic group of ordern, and?(g):=ξg∈C?such thatg?ω=ξgωin H2,0(X) forg∈G.
Theorem 1.2Let X be a K3surface, G be a finite subgroup ofAut(X)such that X/G is smooth.Then the above exact sequence is split, i.e., there is a purely non-symplectic automorphism g∈G such that G is the semidirect product Gs〈g〉of Gsand〈g〉.
Next, we will classify finite Abelian groups which act faithfully onK3 surfaces and the quotient space is smooth.
Definition 1.1We will use the following notations:
Theorem 1.3(see [15])Let X be a K3surface and G be a finite Abelian subgroup ofAut(X)such that the quotient space X/G is isomorphic toP2.Then G is one ofAG∞as a group.Conversely, for every G∈AG∞, there is a K3surface X′and a finite Abelian subgroup G′ofAut(X′)such that X′/G′P2and G′G as a group.
By analyzing the irreducible components of the branch locus of the quotient mapp:X→X/G, we will study a pair (X,G) consisting of aK3 surfaceXand a finite Abelian subgroupGof Aut(X) such that the quotient spaceX/Gis smooth.More precisely, the preimage of the branch locus ofpis∪Fix(g) where Fix(g) := {x∈X:g(x) =x}.Recall that for an automorphismfof finite order of aK3 surface, if Fix(f) contains a curve, thenfis nonsymplectic.The fixed locus of a non-symplectic automorphism is well-known, e.g.[1–2, 14].By analyzing the fixed locus of non-symplectic automorphisms ofGfrom the branch divisor of the quotient map, we will reconstructGfrom the branch divisor of the quotient map.In Section 4,we will investigate the relationship between a branch divisor and exceptional divisors of blowups.Based on the above results, we will obtain our second main result.
Theorem 1.4Let X be a K3surface and G be a finite Abelian subgroup ofAut(X)such that the quotient space X/G is smooth.Then G is one ofAG as a group.Conversely, for every G∈AG, there is a K3surface X′and a finite Abelian subgroup G′ofAut(X′)such that X′/G′is smooth and G′G as a group.
Furthermore, in Section 3, for a Hirzebruch surface Fnand an effective divisorBon Fn,we will give a necessary and sufficient condition for the existence of a finite Abelian coverf:X→Fnsuch thatXis aK3 surface and the branch divisor offisB.In other words, we will solve a part of the Fenchel’s problem for Hirzebruch surfaces.In addition, we will decide the Galois group and give the way to constructf:X→Fnfrom the pair FnandB.
Theorem 1.5Let X be a K3surface and G be a finite Abelian subgroup ofAut(X)such that the quotient space X/G is isomorphic toFn.Then G is one ofAGnas a group.Conversely,for every G∈AGn, there is a K3surface X′and a finite Abelian subgroup G′ofAut(X′)such that X′/G′is isomorphic toFnand G′G as a group.
Subsequently, we will get a similar result for Enriques surfaces.
Definition 1.2We use the following notations:
Theorem 1.6Let E be an Enriques surface and H be a finite subgroup ofAut(E)such that the quotient space E/H is smooth.If there is a birational morphism from E/H to a Hirzebruch surfaceFn, then0 ≤n≤4.In particular, if the quotient space E/H is a Hirzebruch surfaceFn, then n=0,1,2,4.
Theorem 1.7Let E be an Enriques surface and H be a finite Abelian subgroup ofAut(E)such that the quotient space E/H is isomorphic toFn.Then H is one ofAGn(E)as a group.Conversely, for every H′∈AGn(E), there is an Enriques surface E′and a finite Abelian subgroup H′ofAut(E′)such that E′/H′is smooth and H′H as a group.
Theorem 1.8Let E be an Enriques surface and H be a finite Abelian subgroup ofAut(E)such that the quotient space E/H is smooth.Then H is one ofAG(E)as a group.Conversely,for every H∈AG(E), there is an Enriques surface E′and a finite Abelian subgroup H′ofAut(E′)such that E′/H′is smooth and H′H as a group.
Section 2 is preliminaries.In Subsection 3.1, we will give examples for pairs (X′,G′)described in Theorem 1.4.In other words, we will show that for eachG∈AGnwheren= 0,1,2,3,4,6,8,12,there is a pair (X′,G′), whereX′is aK3 surface andG′is a finite Abelian subgroup of Aut(X′)such thatGG′as a group andX′/G′Fn.Furthermore,we will give the way to construct(X′,G′),and we will show that the way to construct(X′,G′)is uniquely determined up to isomorphism from the branch divisor of the quotient mapp:X′→X′/G′.In Subsection 3.2, we will describe branch divisors and Abelian groups for the case where the quotient space is a Hirzebruch surface.In Section 4,first,we will show Theorems 1.1–1.2.Next,we will show that for a pair(X,G)whereXis aK3 surface andGis a finite Abelian subgroup,ifX/Gis smooth, thenGis isomorphic to one of AGas a group.In Section 5, we will show Theorems 1.6–1.8.
2 Preliminaries
We recall the properties of the Galois cover.
Definition 2.1Let f:X→M be a branched covering, where M is a complex manifold and X is a normal complex space.We call f:X→M the Galois cover if there is a subgroup G ofAut(X)such that X/GM and f:X→M is isomorphic to the quotient map p:X→X/GM.We call G the Galois group of f:X→M.Furthermore, if G is an Abelian group,then we call f:X→M the Abelian cover.
Definition 2.2Let f:X→M be a finite branched covering, where M is a complex manifold and X is a normal complex space and ?be the branch locus of f.Let B1,···,Bsbe irreducible hypersurfaces of M and positive integers b1,···,bs, where bi≥2for i= 1,···,s.If ?=B1∪··· ∪Bsand for every j and for any irreducible component D of f?1(Bj)theramification index at D is bj, then we call an effective divisorthe branch divisor of f.
LetXbe a normal projective variety andGbe a finite subgroup of Aut(X).LetY:=X/Gbe the quotient space andp:X→Ybe the quotient map.The branch locus, denoted by?is a subset ofYgiven by?:= {y∈Y| |p?1(y)|<|G|}.It is known that?is an algebraic subset of dimension dim(X) ?1 ifYis smooth (see [19]).Letbe the irreducible components of?whose dimension is 1.LetDbe an irreducible component ofDofp?1(Bj)andGD:= {g∈G:g|D= idD}.Then the ramification index atDisbj:= |GD|, and the positive integerbjis independent of an irreducible component ofp?1(Bj).Thenb1B1+···+brBris the branch divisor ofG.We state the facts (Theorems 2.1–2.2) of the Galois cover theory which we need.
Theorem 2.1(see [12])For a complex manifold M and an effective divisor B on M, if there is a branched covering map f:X→M where X is a simply connected complex manifold X and the branch divisor of f is B, then there is a subgroup G ofAut(X)such that X/GM and f:X→M is isomorphic to the quotient map p:X→X/GM.Furthermore, a pair(X,G)is a unique up to isomorphism.
Theorem 2.2(see [12])For a complex manifold M and an effective divisoron M, where Biis an irreducible hypersurface for i=1,···,n.Let f:X→M be a branched cover whose branch divisor is B and where X is a simply connected complex manifold.Then for a branched cover g:Y→M whose branch divisor isand b′jis divisible by biandm≤n, there is a branched cover h:X→Y such that f=g?h.
LetXbe aK3 surface andGbe a finite subgroup of Aut(X) such thatX/Gis smooth.SinceK3 surfaces are simply connected,Gis determined by the branch divisor of the quotient mapp:X→X/Gfrom Theorem 2.1.In order to classify finite Abelian groupsGwhich act onK3 surfaces and the quotient space is smooth, we will search a smooth rational surfaceSand an effective divisorBonSsuch that there is aK3 surface and a finite subgroupGof Aut(X)such thatX/GSand the branch divisor of the quotient mapp:X→X/GisB.There is the problem which is called Fenchel’s problem.
Problem 2.1LetMbe a projective manifold.Give a necessary and sufficient condition on an effective divisorDonMfor the existence of a finite Galois(resp.Abelian)coverπ:X→Mwhose branch divisor isD.
The Fenchel’s problem was originally for compact Riemann surfaces and was answered by Bundgaard-Nielsen [4] and Fox [5].
Theorem 2.3(see [4–5])Let k≥1and letbe a divisor on a compact Riemann surface M where xi∈M and mi∈Zfor i= 1,···,k.Then there is a finite Galois cover p:X→M such that the branch divisor of p is D except for
(i)M=P1and k=1, and
(ii)M=P1, k=2and m1≠m2.
Furthermore, for the case M=P1, there exists a finite Abelian coverP1→P1whose branchdivisor is D if and only if
(i)k=2and m1=m2or
(ii)k=3and m1=m2=m3=2.
In order to study the cover of the Galois coverX→X/G, the following theorem is useful.
Theorem 2.4Let X be a smooth projective variety, and G be a finite subgroup ofAut(X)such that X/G is smooth.Let p:X→X/G be the quotient map, and B:=b1B1+···+brBrbe the branch divisor of p.Then
where KX(resp.KX/G)is the canonical divisor of X(resp.X/G).
LetXbe aK3 surface andGbe a finite subgroup of Aut(X) such thatX/Gis smooth,andBbe the branch divisor of the quotient mapp:X→X/G.The canonical line bundle of aK3 surface is trivial.By Theorem 2.4, the branch divisor is restricted in the Picard group of the smooth rational surfaceX/G, i.e.,Bmust satisfy
In Subsection 3.1, we will show that for a Hirzebruch surface Fn, if Fnhas an effective divisorwhereBiis an irreducible curve andbi≥2 fori=1,···,k,such thatKS=0 in PicQ(Fn),then 0 ≤n≤12.In Section 4,we will show Theorem 1.1 by using Theorem 2.4.
The following theorem is important for checking the structure ofGfrom the branch divisor.
Theorem 2.5(see [17])For a K3surface X and a finite subgroup G ofAut(X)such that X/G is smooth.Letbe the branch divisor of the quotient map p:X→X/G.We putwhere Ci,jis an irreducible curve for j=1,···,l.Let GCi,j:={g∈G:g|Ci,j= idCi,j}, and Gibe a subgroup of G, which is generated by GCi,1,···,GCi,l, and I?{1,···,k}be a subset.Then, the following holds.
(i)If(X/G)∪i∈IBiis simply connected, then G is generated by{Gj}j∈{1,···,k}I.
(ii)GCi,jZ/biZand GCi,jis generated by a purely non-symplectic automorphism of order bi.
(iii)If G is Abelian, then there is an automorphism g∈G such thatandhence Ci,jare pairwise disjoint.
(iv)If the self-intersection number(Bi·Bi)of Biis positive, then l= 1, and hence Giis generated by a purely non-symplectic automorphism of order bi.
ProofWe will show (i).We assume thatis simply connected.LetHbe the subgroup ofGwhich is generated by {Gj}j∈{1,···,k}I, andThenGandHact onX0.We assume thatG≠H.LetY:=X0/Hbe the quotient space, andG′:=G/H.ThenG′acts faithfully onY,and the branch locus ofY→Y/G′is a finite set.Sinceis smooth and simply connected, this is a contradiction.Therefore,Gis generated by {Gj}j∈{1,···,k}I.
SinceXis aK3 surface, an automorphism whose fixed locus contains a curve can only be purely non-symplectic.Therefore, by the definition of the ramification indexbi, we get (ii).
We will show (iii) and (iv).SinceBiis contained in the branch locus, we getp?1(Bi) =SinceGis finite, for eachj, there issj∈Gsuch thatCi,j?fix(sj).SinceBiis irreducible,we get thatp(Ci,j)=p(Ci,k)for 1 ≤j LetXbe aK3 surface andGbe a finite Abelian subgroup of Aut(X) such thatX/Gis smooth andbe the branch divisor of the quotient mapp:X→X/G.Ifk= 1,then by Theorem 2.5,G=GB1Z/b1Z.We assume thatk= 2.By Theorem 2.5,Gis generated byGB1Z/b1Z andGB2Z/b2Z.Moreover, we assume that the intersectionB1∩B2ofB1andB2is not an empty set.SinceB1∩B2≠ ?,p?1(B1)∩p?1(B2) ≠ ?.Since the fixed locus of an automorphism is a pairwise disjoint set of points and curves, we getGB1∩GB2= {idX}.Therefore,G=GB1⊕GB2, but in the case ofk≥3 it is not necessaryeven ifBi∩Bj≠?for 1 ≤i For an irreducible componentBiofBwe writewhereCjis a smooth curve forj= 1,···,l.Since the degree ofpis |G|, by (iv) of Theorem 2.5, we get that|G|(Bi·Bi)=b2il(Cj·Cj)forj=1,···,l.If the self-intersection number(Bi)2ofBiis positive,then by (iv) of Theorem 2.5, we get thatl= 1 and the genus ofC1is 2 or more.If (Bi)2is zero, thenC1,···,Clare elliptic curves.If (Bi)2is negative, thenC1,···,Clare rational curves.Recall that there isg∈Gsuch thatgis a non-symplectic automorphism of orderbiandC1,···,Clare contained in Fix(g).There are many results on the number of curves,the genus of curves, and the number of isolated points of the fixed locus of a non-symplectic automorphism.We use them to searchBsuch that there is a Galois coverf:X→Ssuch thatXis aK3 surface and the branch divisor offisBand we use them to restoreGfromB.HereSis a smooth rational surface andBis an effective divisor onS. Here, we give the list of a numerical class of an effective divisoron Fnsuch thatBiis a smooth curve for eachi=1,···,kand Definition 3.1For a Hirzebruch surfaceFnwhere n∈Z≥0, we take two irreducible curves C and F such thatPic(Fn) = ZC⊕ZF,(C·F) = 1,(F·F) = 0,(C·C) = ?n andKFn= ?2C?(n+2)F inPic(Fn) = ZC⊕ZF.Notice that for n= 0, C=pr?1OP1(1)and F=pr?2OP1(1), and for n≥1, C is the unique curve onFnsuch that the self-intersection number is negative, and F is the fibre class of the conic bundle ofFn. Lemma 3.1LetFnbe a Hirzebruch surface where n≠ 0and C′?Fnbe an irreducible curve.Then one of the following holds: (1)C′=C. (2)C′=F inPic(Fn). (3)C′=aC+bF where a≥1and b≥na. Definition 3.2Let X be a K3surface and G be a finite subgroup ofAut(X)such that X/GFn.Letbe the branch divisor of the quotient map p:X→X/G.Foreach Bi, there are integers αi,βisuch that Bi=αiC+βiF inPic(Fn).We call as the numerical class of B. Proposition 3.1Let X be a K3surface and G be a finite subgroup ofAut(X)such that X/GFn.Then0 ≤n≤12. ProofWe assume thatX/GFnwheren≥1.LetBbe the branch divisor of the quotient mapp:X→X/G.We writesuch thatBi≠FandB′j=Fin Pic(Fn)fori=1,···,kandj=1,···,l.Since the canonical line bundle of aK3 surface is trivial and Pic(Fn) is torsion free, by Theorem 2.4, we get that SinceBiis an irreducible curve fori=1,···,k,there are integersci,disuch thatBi=ciC+diFin Pic(Fn)and(ci,di)=(1,0)ordi≥nci>0.ByKFn=?2C?(n+2)Fin Pic(Fn)=ZC⊕ZF,we get that We assume that (ci,di) ≠ (1,0) fori= 1,···,k, i.e.,Cis not an irreducible component ofB.Sincedi≥ncifori=1,···,k, bywe get thatwe get 0 ≤n≤2. We assume that(ci,di)=(1,0)for some 1 ≤i≤k,i.e.,Cis an irreducible component ofB.For simplify, we assume thati=1.In the same way as above,we get thatSince 2 ≤b1≤6, we obtain 0 ≤12 ≤n. Notice that by simple calculations, there are not aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GFlforl=10,11. In Section 6, we will give the list of a numerical class of an effective divisoron Fnsuch thatBiis a smooth curve for eachi=1,···,kandin Pic(Fn). LetXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/Gis a Hirzebruch surface Fn, andBbe the branch divisor of the quotient mapp:X→X/G.In this section, we will decide the numerical class ofB.Notice that sinceGis Abelian and the quotient spaceX/Gis smooth, the support ofBand that ofp?Bare simple normal crossing. Furthermore,we will show that the structure as a group ofGdepends only on the numerical class ofBby Theorem 2.5, and we will give the way to constructXandGwhich depends only on the numerical class ofBby Theorem 2.1 and the cyclic cover.As a result the following will follow.For eachG∈AGnwheren= 0,1,2,3,4,6,8,12, there is a pair (X,G′) whereXis aK3 surface andG′is a finite Abelian subgroup of Aut(X) such thatGG′as a group andX/G′Fn.In [9], the case whereGZ/2Z is studied. Theorem 3.1(see [3,Chapter I,Section 17])Let M be a smooth projective variety, and D be a smooth effective divisor on M.Then if the classOM(D)/n∈Pic(M), then there is the Galois cover f:X→M whose branch divisor is nD and the Galois group is isomorphic toZ/nZas a group. Forn≥0, a Hirzebruch surface Fnis isomorphic to a variety Fnin P1×P2, From here, we assume that Fn= Fn.The first projection gives the fibre space structuref:Fn→P1such that the numerical class of the fibre offisF, and is the unique irreducible curve on Fnsuch that the self-intersection number is negative.Letaandbbe positive integers such thatb≥na.Furthermore, we put whereti,j,k∈C, and IfBFis an irreducible curve of Fn, thenBF=aC+bFin Pic(Fn). Letg1andgmbe automorphisms of P1which are induced by matrixes whereζmis anm-th root of unitym≥2.Then 〈g1,g2〉Z/2Z⊕2, and 〈gm〉Z/mZ form≥2.Here for a subsetSof groupG, 〈S〉is the subgroup ofGwhich is generated byS.Then and the quotient maps are isomorphic to form≥2, and the branch divisors are wherex0:=[1:0],x1:=[0:1] andx2:=[1:1]. The above Galois covers P1→P1/〈g1,g2〉P1and P1→P1/〈gm〉P1naturally induce the Galois covers of P1×P1and Fnwhose Galois groups are induced bygmform≥2.We will explain in a bit more detail for Fn.For P1→P1/〈g1,g2〉, let P1×P1Fnbe the fibre product of P1→P1/〈g1,g2〉 andf: Fn→P1.Letp: P1×P1Fn→Fnbe the natural projection of the fibre product.Then andp:P1×P1Fn→Fnis the Galois cover such that the branch divisor ofpis and the Galois group is isomorphic to Z/2Z⊕2as a group, which is induced by〈g1,g2〉.LetCmbe the irreducible curve on Fmsuch that the self-intersection number is negative andFmis the numerical class of the fibre Fm→P1form≥1.Then For P1→P1/〈gm〉, let P1×P1Fnbe the fibre product of P1→P1/〈gm〉 andf: Fn→P1.Letp:P1×P1Fn→Fnbe the natural projection of the fibre product.Then p:P1×P1Fn→Fnis the Galois cover such that the branch divisor ofpis and the Galois group is isomorphic to Z/mZ as a group, which is induced by 〈gm〉, and Definition 3.3From here, we use the notation that(or simply Bi,j)is a smooth curve onFn=iC+jF inPic(Fn)for n≥0, where k∈N. Proposition 3.2For each numerical classes(6.1)–(6.3)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GP1×P1and the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.1)–(6.3). Furthermore, for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X), if X/GP1×P1and the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.1)–(6.3), then G is isomorphic toZ/3Z,Z/3Z⊕2,Z/3Z⊕3, in order, as a group. ProofLetB3,3be a smooth curve on P1×P1.Then the numerical class of 3B3,3is (6.1).By Theorem 3.1, there is the Galois coverp:X→P1×P1such that the branch divisor is 3B3,3and the Galois group is Z/3Z as a group.By Theorem 2.4,the canonical divisor ofXis a numerically trivial.By [18],Xis not a bi-ellitptic surface.By [8],Xis not an Abelian surface.IfXis an Enriques surface, then there is the Galois coverq:X′→P1×P1such thatX′is aK3 surface, the Galois group is Z/2Z ⊕Z/3Z as a group, and the branch divisor is 3B3,3.By Theorem 2.5, this is a contradiction.Therefore,Xis aK3 surface. In addition, let (X′,G′) be a pair of aK3 surfaceX′and a finite Abelian subgroupG′of Aut(X′) such thatX′/G′P1×P1and the numerical class of the branch divisorB′of the quotient mapp′:X′→X′/G′is (6.1).By Theorem 2.5,G′Z/3Z as a group.Since the support ofB′is smooth, there is a smooth curvesuch thatB′=.Then by the above discussion, there is the Galois coverf:X→P1×P1such thatXis aK3 surface, the branch divisor isB′, and the Galois groupGis Z/3Z as a group.Since aK3 surface is simply connected, by Theorem 2.1, the pair (X′,G′) is isomorphic to the pair (X,G). Let,andB1,3be smooth curves on P1×P1such thatis simple normal crossing.Then the numerical class ofis (6.2).Letp:P1×P1→P1×P1be the Galois cover such that the branch divisor isand the Galois group is Z/3Z as a group, which is induced by the Galois cover P1?[z0:z1][z30:z31] ∈P1.Sinceis simple normal crossing,p?B1,3is a reduced divisor on P1×P1such that whose support is a union of pairwise disjoint smooth curves,andp?B1,3=(3,3)in Pic(P1×P1).As for the case of (6.1), there is the Galois coverq:X→P1×P1such thatXis aK3 surface,the Galois group is Z/3Z as a group, and the branch divisor is 3p?B1,3.Then the branched coverp?q:X→P1×P1hasas the branch divisor.SinceXis simply connected, by Theorem 2.1,p?qis the Galois cover.Since the degree ofp?qis 9, by Theorem 2.5, the Galois group ofp?qis Z/3Z⊕2as a group. Conversely, for aK3 surfaceXand a finite Abelian subgroupGof Aut(X) such thatX/GP1×P1and the numerical class of the branch divisorBof the quotient mapp:X→X/Gis (6.2).By the above discussion,Gisomorphic to Z/3Z⊕2as a group, andX→X/Gis given by the composition of the Galois coverX→P1× P1whose numerical class of the branch divisor is (6.1)and the Galois coverp:P1×P1→P1×P1which is induced by the Galois cover P1?[z0:z1][z30:z31]∈P1. As for the case of (6.2), we get the claim for (6.3).In this case, the Galois group is Z/3Z⊕3as a group.Furthermore,letXbe aK3 surface andGbe a finite Abelian subgroup of Aut(X)such thatX/GP1×P1and the numerical class of the branch divisorBofGis (6.3).As for the case of(6.2),X→X/Gis given by the composition of the Galois coverX→P1×P1whose numerical class of the branch divisor is(6.1)and the Galois coverp:P1×P1→P1×P1which is isomorphic to the Galois coverp:P1×P1?([z0:z1],[w0:w1])([z30:z31],[w30:w31])∈P1×P1. For (6.1), we obtain an example if we use a curveB3,3in P1×P1given by the equation For(6.2),we obtain an example if we use curvesin P1×P1given by the equations For (6.3), we obtain an example if we use curvesin P1×P1given by the equations Corollary 3.1For each numerical classes(6.194),(6.83)and(6.302),(6.251),(6.201),(6.84)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.194),(6.83)and(6.302),(6.251),(6.201),(6.84). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.194),(6.83)and(6.302),(6.251),(6.201),(6.84), then G isZ/3Z,Z/2Z ⊕Z/3Z,Z/3Z,Z/2Z ⊕Z/3Z,Z/3Z⊕2,Z/2Z ⊕Z/3Z⊕2, in order, as a group. ProofIn the same way as Proposition 3.2, we get this corollary.More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. i)If the numerical class ofBis one of(6.194),(6.302),thenX→X/Gis given by Theorem 3.1. ii) If the numerical class ofBis (6.83), thenX→X/Gis given by the composition of the Galois coverX′→F2whose numerical class of the branch divisor is (6.194) and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. iii) If the numerical class ofBis one of (6.251), (6.201), (6.84), thenX→X/Gis given by the composition of the Galois coverX′→F6whose numerical class of the branch divisor is(6.302) and the Galois cover F6→Fmwhich is induced by the Galois cover P1→P1of degree6m. For (6.194), we obtain an example if we use a curveB3,6in F2given by the equation For (6.83), we obtain an example if we use curvesin F1given by the equations For (6.302), we obtain an example if we use a sectionCand a curveB2,12in F6given by the equation For (6.251), we obtain an example if we use a sectionCand curvesB2,6in F3given by the equations For (6.201), we obtain an example if we use a sectionCand curvesB2,4in F2given by the equations For (6.84), we obtain an example if we use a sectionCand curvesB2,2in F1given by the equations Proposition 3.3For each numerical classes(6.4)–(6.13)of the list in Section6, there are a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.4)–(6.13). Furthermore, for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X), if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.4)–(6.13),then G isZ/2Z,Z/2Z⊕2,Z/2Z⊕3,Z/2Z⊕Z/4Z,Z/2Z⊕Z/4Z⊕2,Z/2Z⊕2⊕Z/4Z,Z/2Z⊕3,Z/2Z⊕5,Z/2Z⊕4,Z/2Z3⊕Z/4Z, in order, as a group. ProofIn the same way as Proposition 3.2, we get this proposition.More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i) If the numerical class ofBis (6.4), thenX→X/Gis given by Theorem 3.1. (ii) If the numerical class ofBis one of (6.5)–(6.13), thenX→X/Gis given by the composition of the Galois coverX→P1×P1whose numerical class of the branch divisor is(6.4) and the Galois cover P1×P1→P1×P1which is induced by the Galois cover P1→P1. For (6.4), we obtain an example if we use a curveB4,4in P1×P1given by the equation For(6.5),we obtain an example if we use curves2,4in P1×P1given by the equations For (6.6), we obtain an example if we use curves2,2in P1×P1given by the equations For(6.7),we obtain an example if we use curves2,4in P1×P1given by the equations For (6.8), we obtain an example if we use curvesin P1×P1given by the equations For (6.9), we obtain an example if we use curvesin P1×P1given by the equations For (6.10), we obtain an example if we use curvesB1,4in P1×P1given by the equations For(6.11),we obtain an example if we use curvesin P1×P1given by the equations For (6.12), we obtain an example if we use curvesin P1×P1given by the equations For (6.13), we obtain an example if we use curvesin P1×P1given by the equations Corollary 3.2For each numerical classes(6.79)and(6.195),(6.85)and(6.277),(6.202),(6.86),(6.87)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.79)and(6.195),(6.85)and(6.277),(6.202),(6.86),(6.87). Furthermore, for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X), if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.79)and(6.195),(6.85)and(6.277),(6.202),(6.86),(6.87), then G isZ/2Z,Z/2Z,Z/2Z⊕2,Z/2Z,Z/2Z⊕2,Z/2Z ⊕Z/4Z,Z/2Z⊕3, in order, as a group. ProofIn the same way as Proposition 3.2, we get this corollary.More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. i) If the numerical class ofBis one of (6.79), (6.195), (6.277), thenX→X/Gis given by Theorem 3.1. ii)If the numerical class ofBis one of(6.85),thenX→X/Gis given by the composition of the Galois coverX→F2whose numerical class of the branch divisor is (6.195) and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. iii) If the numerical class ofBis one of (6.202) , (6.86), (6.87), thenX→X/Gis given by the composition of the Galois coverX→F4whose numerical class of the branch divisor is(6.277) and the Galois cover F4→Fmwhich is induced by the Galois cover P1→P1of degree. For (6.79), we obtain an example if we use a curveB4,6in F1given by the equation For (6.195), we obtain an example if we use a curveB4,8in F2given by the equation For (6.85), we obtain an example if we use curvesB4,4in F1given by the equations For (6.277), we obtain an example if we use a sectionCand a curveB3,12in F4given by the equation For (6.202), we obtain an example if we use a sectionCand curvesB3,6in F2given by the equations For (6.86), we obtain an example if we use a sectionCand curvesB3,3in F1given by the equations For (6.87), we obtain an example if we use a sectionCand curvesB3,3in F1given by the equations Proposition 3.4For each numerical classes(6.14)–(6.16)of the list in Section6, there are a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.14)–(6.16). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.14)–(6.16), then G isZ/2Z⊕2,Z/2Z⊕3,Z/2Z⊕4, in order, as a group. ProofLetbe smooth curves on P1×P1such thatis simple normal crossing.Then the numerical class ofis (6.14).Since= (2C+ 2F) in Pic(P1×P1),by Theorem 3.1,there are the Galois coverspi:Xi→P1×P1such that the branch divisor ofpiisfori= 1,2 and the Galois group ofpiis isomorphic to Z/2Z as a group fori=1,2.Sinceis simple normal crossing, the fibre productX:=X1×P1×P1X2ofp1andp2is smooth.Therefore, there is the Galois coverp:X→P1×P1such thatXis aK3 surface, the Galois group is isomorphic to Z/2Z⊕2as a group, and the branch divisor isThe rest of this proposition is proved in the same way as Proposition 3.2.More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor ofG.Then we get the following. (i) If the numerical class ofBis (6.14), thenX→X/Gis given by Theorem 3.1 and the fibre product. (ii) If the numerical class ofBis one of (6.15)–(6.16), thenX→X/Gis given by the composition of the Galois coverX→P1×P1whose numerical class of the branch divisor is(6.14) and the Galois cover P1×P1→P1×P1which is induced by the Galois cover P1→P1. For(6.14),we obtain an example if we use curvesin P1×P1given by the equations For (6.15), we obtain an example if we use curvesin P1×P1given by the equations For (6.16), we obtain an example if we use curvesin P1×P1given by the equations Corollary 3.3For each numerical classes(6.80)and(6.196),(6.89)and(6.197),(6.88)and(6.279),(6.203),(6.90),(6.91)of the list in Section6, there is are a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.80)and(6.196),(6.89)and(6.197),(6.88)and(6.279),(6.203),(6.90),(6.91). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.80)and(6.196),(6.89)and(6.197),(6.88)and(6.279),(6.203),(6.90),(6.91), then G isZ/2Z⊕2,Z/2Z⊕2,Z/2Z⊕3,Z/2Z⊕2,Z/2Z⊕3,Z/2Z⊕2,Z/2Z⊕3,Z/2Z⊕2⊕Z/4Z,Z/2Z⊕4, in order, as a group. ProofIn the same way as Proposition 3.2, we get this corollary.More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i) If the numerical class ofBis one of (6.80), (6.196), (6.197), (6.279), thenX→X/Gis given by Theorem 3.1 and the fibre product. (ii) If the numerical class ofBis (6.89), thenX→X/Gis given by the composition of the Galois coverX→F2whose numerical class of the branch divisor is (6.196) and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. (iii) If the numerical class ofBis (6.88), thenX→X/Gis given by the composition of the Galois coverX→F2whose numerical class of the branch divisor is (6.197) and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. (iv) If the numerical class ofBis one of (6.203), (6.90), (6.91), thenX→X/Gis given by the composition of the Galois coverX→F4whose numerical class of the branch divisor is(6.279) and the Galois cover F4→F1which is induced by the Galois cover P1→P1of degree 4. For (6.80), we obtain an example if we use curvesB2,4,B2,2in F1given by the equations For (6.196), we obtain an example if we use curvesin F2given by the equations For (6.89), we obtain an example if we use curvesin F1given by the equations For (6.197), we obtain an example if we use a sectionCand curvesB1,2,B2,6in F2given by the equations For (6.88), we obtain an example if we use a sectionCand curvesB1,1,B2,3in F1given by the equations For (6.279), we obtain an example if we use a sectionCand curvesB1,4,B2,8in F4given by the equations For (6.203), we obtain an example if we use a sectionCand curvesB1,2,B2,4in F2given by the equations For (6.90), we obtain an example if we use a sectionCand curvesB1,1,B2,2in F1given by the equations For (6.91), we obtain an example if we use a sectionCand curvesB1,1,B2,2in F1given by the equations A lattice is a pair (L,b) of a free Abelian groupL:=Z⊕nof ranknand a symmetric non-degenerate bilinear formb:L×L→Z taking values in Z.The discriminant group ofLisL∨/L, where the dualL∨:= {m∈L?Q |b(m,l)∈Z for alll∈L} (here we denote bybthe Q linear extension ofb).LetUbe the hyperbolic lattice, andAnand letEnbe the negative definite lattices of ranknassociated to the corresponding root systems. Proposition 3.5For each classes(6.17)–(6.18)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.17)–(6.18). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.17)–(6.18), then G isZ/3Z⊕2,Z/3Z⊕2, in order, as a group. ProofLet,andbe smooth curves such thatis simple normal crossing.Sincein Pic(P1×P1), by Theorem 3.1, there is the Galois coverp′:X′→P1×P1such that the branch divisor isand the Galois group is isomorphic to Z/3Z as a group.Sinceis simple normal crossing, singular points ofX′are rational double points.More precisely, the singular locus ofX′consists of sixA2points.Letpm:X′m→X′be the minimal resolution ofX′.Then the canonical divisor ofX′mis numerical trivial.SinceX′mhas a curve such that the self-intersection number is negative,X′mis aK3 surface or Enriques surface.SinceX′mhas an automorphismsof order 3 such that the curves of Fix(s) are three rational curvesCifori= 1,2,3, by [11],X′mis aK3 surface.By [1, Theorem 2.8 and Proposition 3.2] or [14, Table 2], we get that Letz1,···,z6be singular points ofX′, ande1,···,e12be the exceptional divisors ofpm,wherezi=pm(e2i?1) =pm(e2i) fori= 1,···,6.Notice that (e2i?1·e2i) = 1, (e2i?1·e2i?1) = ?2 and(e2i·e2i)=?2.SinceCi?Fix(s) fori=1,2,3,we get that (e2i?1∪e2i)∩Fix(s) contains at least 2 points.Sinces(e2i?1∪e2i) = (e2i?1∪e2i) ande2i?1∩e2iis one point, we get thate2i?1∩e2i?Fix(s).Therefore,s(e2i?1) =e2i?1ands(e2i) =e2i, and hencee2i?1,e2i∈Pic(X′m)s?fori= 1,···,6.Since Pic(X′m)s?is a primitive sublattice, the minimal primitive sublattice which contains (p′?pm)?Pic(P1×P1) ande1,···,e12of Pic(X′m) is Pic(X′m)s?. Letf:=p′?pm:X′m→P1×P1.Sincef?Ci=Bi1,1, we get (Ci·f?F)=((C+F)·F)=1 fori=1,2,3.Let Then (C′1·ei) = 0 fori= 1,···,12.Since (e2i?1·e2i?1) = ?2, (e2i?1·e2i?1+2e2i) = 0 and(e2i?1+2e2i·e2i?1+2e2i) = ?6, we get 6C′1∈Pic(X′m).Therefore, the minimal primitive sublatticeKof Pic(X′m)s?, which containsf?Cand 6C′1is a unimodular lattice.LetMbe the minimal primitive sublattice of Pic(X′m), which contains the curvese1,···,e12.ThenM?U⊥.SinceUis a unimodular lattice andMandUare sublattice of Pic(X′m)s?, we getU⊕M= Pic(X′m)s?.Therefore, the rank ofMis 12 andM∨/MZ/3Z⊕4.Thus, by[6,Theorem 5.2] there is aK3 surfaceXand a symplectic automorphismtof order 3 ofXsuch thatX′=X/〈t〉, and hence there is a finite Abelian subgroupG?Aut(X) such thatX/GP1×P1,GZ/3Z⊕2, and the branch divisor isIn the same way, we get the claim for (6.18). More specifically, letXbe aK3 surfaceX,Gbe a finite Abelian subgroupGof Aut(X)such thatX/GP1×P1, and the numerical class of the branch divisorBofGis (6.17) or(6.18).By Theorem 3.1, there is the Galois coverp′:X′→P1×P1such that the branch divisor isBand the Galois group is isomorphic to Z/3Z as a group.Then we get thatXis the universal cover ofX′of degree 3. For (6.17), we obtain an example if we use curvesin P1×P1given by the equations For (6.18), we obtain an example if we use curvesB1,0,B1,1,B1,2in P1× P1given by the equations Corollary 3.4For each numerical classes(6.198),(6.92)and(6.204)and(6.303),(6.252),(6.205),(6.93)of the list in Section6,there are a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class B of the branch divisor of the quotient map p:X→X/G is(6.198),(6.92)and(6.204)and(6.303),(6.252),(6.205),(6.93). Furthermore, for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X), if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.198),(6.92)and(6.204)and(6.303),(6.252),(6.205),(6.93), then G isZ/3Z⊕2,Z/2Z ⊕Z/3Z⊕2,Z/3Z⊕2,Z/3Z⊕2,Z/2Z ⊕Z/3Z⊕2,Z/3Z⊕3,Z/2Z ⊕Z/3Z⊕3, in order, as a group. ProofIn the same way as Proposition 3.5, we get this corollary.More specifically, letXbe aK3 surfaceX,Gbe a finite Abelian subgroupGof Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Letp′:X′→P1×P1be the Galois cover such that the branch divisor isBand which is given by Theorem 3.1.Then we get the following. (i) If the numerical class ofBis one of (6.198), (6.204), (6.303), thenXis the universal cover ofX′of degree 3. (ii) If the numerical class ofBis (6.92), thenX→X/Gis given by the composition of the Galois coverX′→F2whose numerical class of the branch divisor is(6.92)and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. (iii) If the numerical class ofBis one of (6.252), (6.205), (6.93), thenX→X/Gis given by the composition of the Galois coverX′→F6whose numerical class of the branch divisor is(6.303) and the Galois cover F6→Fmwhich is induced by the Galois cover P1→P1of degree6m. For (6.198), we obtain an example if we use curvesin F2given by the equations For (6.92), we obtain an example if we use curvesin F1given by the equations For (6.204), we obtain examples if we use a sectionCand curvesin F2given by the equations For (6.303), we obtain examples if we use a sectionCand curvesin F6given by the equations For (6.252), we obtain examples if we use a sectionCand curvesin F3given by the equations For (6.205), we obtain examples if we use a sectionCand curvesin F2given by the equations For(6.93),we obtain examples if we use a sectionCand curvesin F1given by the equations Proposition 3.6For each numerical classes(6.19)–(6.20)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.19)–(6.20). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.19)–(6.20), then G isZ/2Z⊕3,Z/2Z⊕3, in order, as a group. ProofLetBi1,1be a smooth curve on P1×P1fori=1,2,3,4 such thatis simple normal crossing.Then the numerical class ofis (6.19).We setandLetZ:= Blow{x1,x2,x3,x4}P1×P1.LetEibe the exceptional divisor fori= 1,2,3,4.ThenLetCibe the proper transform offori=1,2,3,4.Then fori=1,2,j=3,4, By Theorem 3.1, there are the Galois coversp1:Y1→Zandp2:Y2→Zsuch that the branch divisor ofp1is 2C1+2C2,and that ofp2is 2C3+2C4.SinceC1∩C2andC3∩C4are empty sets,Y1andY2are smooth.Sinceis simple normal crossing,Y:=Y1×ZY2is smooth and aK3 surface.Therefore, there is the Galois coverf:Y→Zwhose branch divisor isand Galois group is Z/2Z⊕2as a group.LetC′ibe a smooth curve onYsuch thatf?Ci=2C′ifori=1,2,3,4.Then Thus, we get By Theorem 3.1, there is the Galois coverg:W→Ywhose branch divisor isLetE′ibe a smooth curve onWsuch thatg?f?Ei=2E′i.Since (f?Ei·f?Ei)=?2, (E′i·E′i)=?1 fori=1,2,3,4.Letf:W→Xbe a contraction ofE′1,···,E′4.SinceYis aK3 surface,Xis aK3 surface.SinceWis a double cover ofY, there is a symplectic involutionsofXsuch thatX/〈s〉→P1×P1is a Galois cover whose branch divisor isTherefore,there is a finite Abelian subgroupG?Aut(X) such thatX/GP1×P1,GZ/2Z⊕3, and the branch divisor is Next,letB1,0,B1,2be smooth curves on P1×P1such thatis simple normal crossing.Then the numerical class ofis (6.20).We set {x1,x2}:=B1,0∩B1,2andLetZ:=Blow{x1,x2,x3,x4}P1×P1.LetEibe the exceptional divisor fori= 1,2,3,4.ThenLetbe the proper transform ofin order.Then Letp1:Y1→Zbe a cyclic cover whose branch divisor is 2C1,0+2C1,2, andp2:Y2→Zbe a cyclic cover whose branch divisor isThen as for the case of(6.19),Y:=Y1×ZY2is aK3 surface, and there is the Galois coverf:Y→Zwhose branch divisor isand Galois group is to Z/2Z⊕2as a group.Sinceandwe getAs for the case of (6.19), we getand hence we get the claim for (6.20). More specifically, letXbe aK3 surfaceX,Gbe a finite Abelian subgroupGof Aut(X)such thatX/GP1×P1, and the numerical class of the branch divisorBof the quotient mapp:X→X/Gis (6.19) or (6.20).By Theorem 3.1 and the fibre product, there is the Galois coverp′:X′→P1×P1such that the branch divisor isBand the Galois group is Z/2Z⊕2as a group.Then we get thatXis the universal cover ofX′of degree 2. For (6.19), we obtain an example if we use curvesgiven by the equations For (6.20), we obtain an example if we use curvesin P1×P1given by the equations Corollary 3.5For each numerical classes(6.81)and(6.82)and(6.199),(6.94)and(6.200),(6.96)and(6.282),(6.206),(6.97),(6.98)of the list in Section 6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.81)and(6.82)and(6.199),(6.94)and(6.200),(6.96)and(6.282),(6.206),(6.97),(6.98). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.81)and(6.82)and(6.199),(6.94)and(6.200),(6.96)and(6.282),(6.206),(6.97),(6.98), then G isZ/2Z⊕3,Z/2Z⊕3,Z/2Z⊕3,Z/2Z⊕4,Z/2Z⊕3,Z/2Z⊕4,Z/2Z⊕3,Z/2Z⊕4,Z/2Z⊕3⊕Z/4Z,Z/2Z⊕5, in order, as a group. ProofIn the same way as Proposition 3.6, we get this corollary.More specifically, letXbe aK3 surfaceX,Gbe a finite Abelian subgroupGof Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i)We assume that the numerical class ofBis one of(6.81),(6.82),(6.199),(6.200),(6.282).By Theorem 3.1 and the fibre product, there is the Galois coverp′:X′→Fnsuch that the branch divisor isBand the Galois group is Z/2Z⊕2as a group.ThenXis the universal cover ofX′of degree 2. (ii) If the numerical class ofBis (6.94), thenX→X/Gis given by the composition of the Galois coverX→F2whose numerical class of the branch divisor is (6.199) and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. (iii) If the numerical class ofBis (6.96), thenX→X/Gis given by the composition of the Galois coverX→F2whose numerical class of the branch divisor is (6.200) and the Galois cover F2→F1which is induced by the Galois cover P1→P1of degree 2. (iv) If the numerical class ofBis one of (6.206), (6.98), (6.97), thenX→X/Gis given by the composition of the Galois coverX→F4whose numerical class of the branch divisor is(6.303) and the Galois cover F4→Fmwhich is induced by the Galois cover P1→P1of degree. For (6.81), we obtain an example if we use a sectionCand curvesin F1given by the equations For (6.82), we obtain an example if we use curvesin F1given by the equations For (6.199), we obtain an example if we use a sectionCand curvesin F2given by the equations For (6.94), we obtain an example if we use a sectionCand curvesin F1given by the equations For (6.200), we obtain an example if we use curvesin F2given by the equations For (6.96), we obtain an example if we use curvesin F1given by the equations For (6.282),we obtain an example if we use a sectionCand curvesin F4given by the equations For (6.206), we obtain examples if we use a sectionCand curvesin F2given by the equations For (6.97), we obtain examples if we use a sectionCand curvesB11,1,B21,1,B31,1,B10,1,B20,1in F1given by the equations For (6.98), we obtain an example if we use a sectionCand curvesB11,1,B21,1,B31,1,B10,1,B20,1,B30,1in F1given by the equations Proposition 3.7For numerical classes(6.278),(6.207),(6.99),(6.100)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.278),(6.207),(6.99),(6.100). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.278),(6.207),(6.99),(6.100), then G isZ/4Z,Z/2Z ⊕Z/4Z,Z/4Z⊕2,Z/2Z2⊕Z/4Z, in order, as a group. ProofLetB2,8be a smooth curve on F4.Then the numerical class of 2C+4B2,8is(6.278).SinceB2,8=2C+8Fin Pic(F4), by Theorem 3.1, there is the Galois coverp1:X1→F4such that the branch divisor is 2B2,8and the Galois group is Z/2Z as a group.LetE2,8be a smooth curve onX1such thatp?1B2,8= 2E2,8.SinceC+B2,8is simple normal crossing,p?1Cis a reduced divisor onX1, whose support is a union of pairwise disjoint smooth curves.Sincep?1C+E2,8=p?1(2C+4F)=2p?1(C+2F) in Pic(X1), by Theorem 3.1, there is a Galois coverp2:X2→X1such that the branch divisor isp?1C+E2,8and the Galois group is Z/2Z as a group.Thenp:=p1?p2:X2→F4is the branched cover such thatphas 2C+4B2,8as the branch divisor.In the same way of Proposition 3.2,Xis aK3 surface, andp:X→F4is the Galois cover whose Galois group is Z/4Z as a group.In the same way of Proposition 3.2, we get the claim for (6.207), (6.99), (6.100). More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i) If the numerical class ofBis (6.278), thenX→X/Gis given by the above way. (ii) If the numerical class ofBis one of (6.207), (6.99), (6.100), thenX→X/Gis given by the composition of the Galois coverX′→F4whose numerical class of the branch divisor is(6.278) and the Galois cover F4→Fmwhich is induced by the Galois cover P1→P1of degree. For (6.278),we obtain an example if we use a sectionCand a curveB2,8in F4given by the equation For (6.207), we obtain examples if we use a sectionCand curvesB2,4,B10,1,B20,1in F2given by the equations For (6.99), we obtain examples if we use a sectionCand curvesB2,2,B10,1,B20,1in F1given by the equations For (6.100), we obtain examples if we use a sectionCand curvesB2,2,B10,1,B20,1,B30,1in F1given by the equations Proposition 3.8For numerical classes(6.280),(6.208)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.280),(6.208). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.280),(6.208), then G isZ/2Z ⊕Z/4Z,Z/2Z⊕2⊕Z/4Z, in order, as a group. ProofLetB1,6andB1,4be smooth curves on F4such thatC+B1,6+B1,4is simple normal crossing.Then the numerical class of 4C+2B1,6+4B1,4is(6.280).SinceC+B1,4=2C+2Fin Pic(F8), by Theorem 3.1,there is the Galois coverp1:X1→F4such that the branch divisor is 2C+2B1,4and the Galois group is Z/2Z as a group.LetEC,E1,4be two smooth curves onX1such thatp?1C=2ECandp?1B1,4=2E1,4.SinceC+B1,6+B1,4is simple normal crossing,p?1B1,6is a reduced divisor onX1, whose support is a union of pairwise disjoint smooth curves.Sincep?1B1,6=p?1(C+6F)=p?1(C+4F)+p?1(2F)=2E1,4+2p?1Fin Pic(X1), by Theorem 3.1,there is the Galois coverp2:X2→X1such that the branch divisor is 2p?1B1,6and the Galois group is Z/2Z.Notice thatSinceC+B1,6+B1,4is simple normal crossing,p?2ECandp?2E1,4are reduced divisors onX2,whose support are unions of pairwise disjoint smooth curves.Sincep?2(EC+E1,4)=p?2p?1(C+2F)=p?2p?1(C+6F)?p?2p?14F=p?2p?1B1,6?4p?2p?1Fin Pic(X2)andby Theorem 3.1, there is the Galois coverp3:X→X2such that the branch divisor isp?2(EC+E1,4) and the Galois group is Z/2Z.Thenp:=p1?p2?p3:X→F4is the branched cover such thatphas 4C+2B1,6+4B1,4as the branch divisor.In the same way of Proposition 3.2,Xis aK3 surface, andp:X→F4is the Galois cover whose Galois group is Z/2Z ⊕Z/4Z as a group.In the same way of Proposition 3.2, we get the claim for(6.208). More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i) If the numerical class ofBis (6.280), thenX→X/Gis given by the above way. (ii) If the numerical class ofBis (6.208), thenX→X/Gis given by the composition of the Galois coverX′→F4whose numerical class of the branch divisor is (6.280)and the Galois cover F4→F2which is induced by the Galois cover P1→P1of degree 2. For (6.280), we obtain an example if we use a sectionCand curvesB1,6,B1,4in F4given by the equations For (6.208), we obtain an example if we use a sectionCand curvesB1,3,B1,2,B10,1, B20,1in F2given by the equations Corollary 3.6For each numerical classes(6.311),(6.281),(6.210),(6.209),(6.101)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.311),(6.281),(6.210),(6.209),(6.101). Furthermore,for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X),if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.311),(6.281),(6.210),(6.209),(6.101), then G isZ/2Z ⊕Z/4Z,Z/2Z⊕2⊕Z/4Z,Z/2Z⊕3⊕Z/4Z,Z/2Z ⊕Z/4Z⊕2,Z/2Z ⊕Z/4Z ⊕Z/8Z, in order, as a group. ProofIn the same way Proposition 3.8, we get the claim.More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i) If the numerical class ofBis (6.311), thenX→X/Gis given by the above way. (ii) If the numerical class ofBis one of (6.101), (6.209), (6.210), (6.281), thenX→X/Gis given by the composition of the Galois coverX→F8whose numerical class of the branch divisor is (6.311) and the Galois cover F8→Fmwhich is induced by the Galois cover P1→P1of degree. For (6.311), we obtain examples if we use a sectionCand curvesB11,8,B21,8in F8given by the equations For (6.281), we obtain examples if we use a sectionCand curvesB11,4,B21,4,B10,1, B20,1in F4given by the equations For (6.209), we obtain examples if we use a sectionCand curvesB11,2,B21,2,B10,1, B20,1in F2given by the equations For (6.101), we obtain examples if we use a sectionCand curvesB11,1,B21,1,B10,1, B20,1in F1given by the equations For (6.210), we obtain an example if we use a sectionCand curvesB11,2,B21,2,B10,1,B20,1,B30,1in F2given by the equations Proposition 3.9For each numerical classes(6.316),(6.304),(6.283),(6.254),(6.253),(6.211),(6.95)of the list in Section6, there is a K3surface X and a finite Abelian subgroup G ofAut(X)such that X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.316),(6.304),(6.283),(6.254),(6.253),(6.211),(6.95). Furthermore, for a pair(X,G)of a K3surface X and a finite Abelian subgroup G ofAut(X), if X/GFnand the numerical class of the branch divisor B of the quotient map p:X→X/G is(6.316),(6.304),(6.283),(6.254),(6.253),(6.211),(6.95),then G isZ/2Z⊕Z/3Z,Z/2Z⊕2⊕Z/3Z,Z/2Z ⊕Z/3Z⊕2,Z/2Z⊕3⊕Z/3Z,Z/2Z ⊕Z/3Z ⊕Z/4Z,Z/2Z⊕2⊕Z/3Z⊕2,Z/2Z ⊕Z/3Z⊕2⊕Z/4Z, in order, as a group. ProofLetBi1,12be a smooth curve on F12fori= 1,2 such thatC+B11,12+B21,12is simple normal crossing.Then the numerical class of 6C+2B11,12+3B21,12is (6.316).SinceC+B11,12= 2C+12Fin Pic(F12), by Theorem 3.1, there is the Galois coverp1:X1→F12such that the branch divisor is 2C+2B11,12and the Galois group is Z/2Z as a group.SinceC+B11,12+B21,12is simple normal crossing,p?1B21,12is a reduced divisor onX1, whose support is a union of pairwise disjoint smooth curves.SinceCandB11,12are smooth curves, there are smooth curvesEC,E11,12onX1such thatp?1C= 2ECandp?1B11,12= 2E11,12.SinceEC+p?1B21,12=EC+p?1(C+12F)=EC+p?1C+12p?1F=3EC+12p?1Fin Pic(X1),by Theorem 3.1, there is the Galois coverp2:X→X1such that the branch divisor is 3EC+3p?1B21,12and the Galois group is Z/3Z as a group.Thenp:=p1?p2:X→F12is the branched cover such thatphas 6C+2B11,12+3B21,12as the branch divisor.In the same way as Proposition 3.2,Xis aK3 surface, andp:X→F12is the Galois cover whose Galois group isGZ/2Z ⊕Z/3Z as a group. More specifically, letXbe aK3 surface,Gbe a finite Abelian subgroup of Aut(X) such thatX/GFn, andBbe the branch divisor of the quotient mapp:X→X/G.Then we get the following. (i) If the numerical class ofBis (6.316), thenX→X/Gis given by the above way. (ii) If the numerical class ofBis one of (6.304), (6.283), (6.254), (6.253), (6.211), (6.95),thenX→X/Gis given by the composition of the Galois coverX′→F12whose numerical class of the branch divisor is (6.316) and the Galois cover F12→Fmwhich is induced by the Galois cover P1→P1of degree. For(6.316),we obtain an example if we use a sectionCand curvesB11,12,B21,12in F12given by the equations For (6.304), we obtain examples if we use a sectionCand curvesB11,6,B21,6,B10,1,B20,1in F6given by the equations For (6.283), we obtain examples if we use a sectionCand curvesB11,4,B21,4,B10,1,B20,1in F4given by the equations For (6.253), we obtain examples if we use a sectionCand curvesB11,3,B21,3,B10,1,B20,1in F3given by the equations For (6.211), we obtain examples if we use a sectionCand curvesB11,2,B21,2,B10,1,B20,1in F2given by the equations For (6.95), we obtain examples if we use a sectionCand curvesB11,1,B21,1,B10,1,B20,1in F1given by the equations For (6.254), we obtain an example if we use a sectionCand curvesB11,3,B21,3,B10,1,B20,1,B30,1in F3given by the equations In this section, we will show that there is no numerical class such that it has an AbelianK3 cover except the numerical classes which are mentioned in Subsection 3.1.Then by Subsection 3.1, we will get Theorem 1.5.From here, we use the notations that (i)Xis aK3 surface, (ii)Gis a finite Abelian subgroup of Aut(X) such thatX/GFn, (iii)p:X→X/Gis the quotient map, and (iv)is the branch divisor ofp. Furthermore, we use the notation that(or simplyBi,j) is a smooth curve on Fnsuch that=iC+jFin Pic(Fn) ifn≥0 wherek∈N. For the branch divisorwherem,n(i)∈N, we use the notation that Recall that by Theorem 2.5,is a cyclic group of orderbijwhich is generated by a nonsymplectic automorphism of orderbij.SinceGis Abelian, the support ofBand the support ofp?Bare simple normal crossing. Lemma 3.2We assume that X/GFnfor n≥1.If inPic(Fn), where a,bi,dj≥2and ci,l≥1, then3 ≥l≥2and d1=···=dl. ProofBy Theorem 2.5, there are pairwise disjoint smooth curvesC1,···,Cmsuch thatSinceC1,···,Cmare pairwise disjoint, we get that(Ci·Ci)=m(Ci·Ci)fori=1,···,m.Since (C·C)=?n<0, (Ci·Ci)<0 fori=1,···,m.SinceXis aK3 surface,Ciis a smooth rational curve fori= 1,···,m.Letp|Ci:Ci→Cbe the finite map.LetBci,ncibe an irreducible curve on Fn.SinceBci,nci=ciC+nciFin Pic(Fn),we get thatC∩Bci,nciis an empty set.Since the support ofBis simple normal crossing,p|Ciis the Galois covering whose branch divisor isIfdi≠dj, thenp|Cimust be non-trivial.SinceGis an Abelian group,p|Ciis the Abelian cover, however by Theorem 2.3,this is a non-Abelian cover.This is a contradiction.Therefore,d1=···=dl. By Lemma 3.2, the numerical class ofBis not one of (6.128), (6.129), (6.132), (6.137),(6.143), (6.150), (6.151), (6.152), (6.154), (6.159), (6.160), (6.162), (6.170), (6.171), (6.172),(6.173), (6.174), (6.175), (6.179), (6.188), (6.193), (6.220), (6.227), (6.230), (6.235), (6.247),(6.248), (6.255), (6.256), (6.257), (6.264), (6.269), (6.271), (6.274), (6.276), (6.285), (6.288),(6.290), (6.295), (6.297), (6.301), (6.307), (6.310), (6.313), (6.315) of the list in Section 6. Lemma 3.3We assume that X/GFnfor n≥1.Ifwherea,bi,dj≥2, then d1=···=dl,and bi=d1if(C·Bi)≠0for i=1,···,k. ProofIn the same way of Lemma 3.2, we get that forthe finite mapp|Ci:Ci→Cis the Abelian cover between P1whose branch divisor isand Galois group is {g∈G:|g(C1)=C1}.By Theorem 2.3, we get the claim. By Lemma 3.3, the numerical class ofBis not one of (6.127), (6.133), (6.134), (6.135),(6.145), (6.146), (6.156), (6.157), (6.158), (6.161), (6.163), (6.164), (6.165), (6.166), (6.167),(6.168), (6.169), (6.223), (6.224), (6.225), (6.236), (6.237), (6.238), (6.239), (6.240), (6.261),(6.262), (6.263), (6.268), (6.270), (6.272), (6.273), (6.275), (6.284), (6.289), (6.292), (6.296),(6.298), (6.299), (6.300), (6.306), (6.312), (6.314) of the list in Section 6. Lemma 3.4If there are irreducible curves B1and B2and positive even integers b1,b2≥2such that B=b1B1+b2B2and(B1·B2)≠0, then(B1·B2)=8. ProofBy Theorem 2.5,G=GB1⊕GB2andGBiZ/biZ fori= 1,2.Letsi∈GBibe a generator fori= 1,2.SinceGis Abelian,is a symplectic automorphism of order 2.SinceX/Gis smooth,Since the support ofBis simple normal crossing and |G| =b1b2, we get that |p?1(B1)∩p?1(B2)| = (B1·B2).By the fact that the fixed locus of a symplectic automorphism of order 2 are 8 isolated points, we get that(B1·B2)=8. By Lemma 3.4, the numerical class ofBis not one of (6.21), (6.25), (6.26), (6.28), (6.103),(6.112), (6.130), (6.176), (6.213), (6.216), (6.241) of the list in Section 6. Lemma 3.5If there are irreducible curves B1and B2such that B= 3B1+ 3B2and(B1·B2)≠0, then(B1·B2)=3. ProofBy Theorem 2.5,G=GB1⊕GB2andGBiZ/3Z fori= 1,2.Letsi∈GBibe a generator fori= 1,2.SinceGis Abelian, we may assume thats1?s2is a non-symplectic automorphism of order 3.By Theorem 2.5, Fix(s1?s2) does not contain a curve.Then by [1,Theorem 2.8] or [14, Table 2], Fix(s1?s2) is only three isolated points.SinceX/Gis smooth,Fix(s1?s2)=p?1(B1)∩p?1(B2).SinceB1+B2is simple normal crossing andG=GB1⊕GB2,we get that |p?1(B1)∩p?1(B2)|=(B1·B2).Therefore, we get (B1·B2)=3. By Lemma 3.5, the numerical class ofBis not one of (6.22), (6.23), (6.212), (6.218) of the list in Section 6. Lemma 3.6If there are irreducible curves Biand positive integers bi≥2for i=1,···,k such thatand G=GBifor some i, then(Bi·Bj)=0for j≠i. ProofRecall that by Theorem 2.5,GBmis generated by a non-symplectic automorphism of orderbmand Fix(GBm) ?p?1(Bm) form= 1,···,k.If (Bi·Bj) ≠ 0 forj≠ 0, thenp?1(Bi)∩p?1(Bj) is not an empty set.By the fact that the fixed locus of an automorphism is a pairwise set of points and curves, this is a contradiction. By Lemma 3.6,the numerical class ofBis not one of(6.24),(6.131),(6.177),(6.219),(6.242)of the list in Section 6. Lemma 3.7If there are irreducible curves B1and B2such that B= 2B1+ 2B2and(B1·B2)≠0, then ProofBy Theorem 2.5,G=GB1⊕GB2andGBiZ/2Z fori= 1,2.Since the fixed locus of a non-symplectic automorphism of order 2 is a set of pairwise set of smooth curves or empty set,X/GBiis smooth.Then there is a double coverX/GBi→X/GFnwhose branch divisor is 2Bjfori,j=1,2 andi≠j.By Theorem 3.1,∈Pic(Fn) fori=1,2. By Lemma 3.7, the numerical class ofBis not one of (6.27), (6.113), (6.117) of the list in Section 6. Lemma 3.8If there are irreducible curves B1,B2,B3such that B=2B1+3B2+6B3and(B2·B2)≥1and(Bi·Bj)≠0for1 ≤i ProofTheorem 2.5,GB1Z/2Z,GB2Z/3Z,GB3Z/6Z.Since (Bi·Bj) ≠ 0 for 1 ≤i < j≤3, we getGB1⊕GB2∩GB3= {idX}.Therefore,G=GB1⊕GB2⊕GB3.Since(B2·B2)>0, we get thatp?B2=3C2and the only curve of Fix(GB2) isC2. We assume that (B2·B2)≥2.Since |G|=36,(C21,1·C21,1)≥8, and hence the genus ofC21,1is at least 5.By [1,14] and the only curve of Fix(GB2) isC2, this is a contradiction. By Lemma 3.8, the numerical class ofBis not one of(6.29), (6.214)of the list in Section 6. Lemma 3.9If there are irreducible curves B1,B2,B3such that B=2B1+4B2+4B3and(Bi·Bj)≠0for1 ≤i ProofTheorem 2.5,GB1Z/2Z andGBiZ/4Z fori= 2,3.Since (Bi·Bj) ≠ 0 for 1 ≤i < j≤3, we getGB1∩(GB2⊕GB3) = {idX}.Therefore,G=GB1⊕GB2⊕GB3.Lets∈GB1andt∈GB2be generators.Thens?tis a non-symplectic automorphism of order 4 andp?1(B1)∩p?1(B2) ?Fix(s?t).By Theorem 2.5 andG=GB1⊕GB2⊕GB3, Fix(s?t)does not contain a curve.By [2, Proposition 1], the number of isolated points of Fix(s?t) is 4.If (B1·B2)≥2, then |p?1(B1)∩p?1(B2)|≥8.This is a contradiction. By Lemma 3.9, the numerical class ofBis not (6.30), (6.109), (6.155), (6.215)of the list in Section 6. Lemma 3.10We assume that X/GP1×P1.Then B≠a({q}×P1)+bC1+cC2where C1and C2are smooth curves onP1×P1, C1∩C2≠?, and a,b,c are even integers. ProofWe assume thatB=a({q}×P1)+bC1+cC2whereC1andC2are smooth curves on P1×P1,C1∩C2≠ ?, anda,b,care even integers.SinceC1∩C2≠ ?, by Theorem 2.5,G=GC1⊕GC2.Sinceb,care even integers,GC1,GC2are cyclic groups, andG=GC1⊕GC2,the number of non-symplectic involution ofGis 2.Since (B1,0·Ci)≠0 andais even,Gmust have at least 3 non-symplectic involutions.This is a contradiction. By Lemma 3.10, the numerical class ofBis not one of (6.31), (6.32), (6.33), (6.35), (6.36),(6.37), (6.38) of the list in Section 6. Lemma 3.11If there are irreducible curves Biand positive integers bi≥2for i=1,···,k such thatG=GB1⊕GB2and b1and b2are coprime, then for each i= 1,2,j=3,···,k, we get that biand bjare coprime if(Bi·Bj)≠0. ProofLets∈GB1andt∈GB2be generators.By Theorem 2.5, the order ofsisb1and that oftisb2.SinceG=GB1⊕GB2, there are integersuandvsuch thatGBjis generated bysu?tv. We assume that (B1·Bj)≠0 andb1andbjare not coprime.Sinceb1andb2are coprime,there is an integerlsuch that(su?tv)l≠idXand(su?tv)l=smortm.Sinceb1andbjare not coprime, we assume that(su?tv)l=sm.Thenp?1(B1) andp?1(Bj)are contained in Fix(sm).By the fact that the fixed locus of an automorphism is a pairwise set of points and curves, this is a contradiction. By Theorem 2.5 and Lemma 3.11, the numerical class ofBis not one of (6.34), (6.40),(6.265), (6.266), (6.293), (6.294), (6.308), (6.309) of the list in Section 6. We assume that the numerical class ofBis (6.39) of the list in Section 6.We denoteBby 3B1,0+3B2,2+3B0,1.By Theorem 2.5,G=G2,2.SinceG2,2Z/3Z,Ghas 1 subgroups generated by a non-symplectic automorphism of order 3.Since (B1,0·B2,2)≠0,Gcontains at least 2 such a subgroup from Theorem 2.5.This is a contradiction. Lemma 3.12If there are irreducible curves B1,B2,B3such that B= 2B1+2B2+2B3,and(Bi·Bj)≠0for1 ≤i ProofBy Theorem 2.5,GBiZ/2Z fori=1,2,3.Since (Bi·Bj)≠0 for 1 ≤i We assume that (B1·B2)=4.Thenp?1(B1)∩p?1(B2) is a set of 8 points.Since the fixed locus of a symplectic automorphism of order 2 is a set of 8 isolated points,X/GB1⊕GB2is smooth.Then there is a double coverX/GB1⊕GB2→X/GFnwhose branch divisor is 2B3.Thus,fori=1,2. By Lemma 3.12, the numerical class ofBis not one of (6.41), (6.119), (6.122), (6.217) of the list in Section 6. Lemma 3.13If there are irreducible curves B1,B2,B3such that B= 2B1+2B2+2B3,and(Bi·Bj)≠0for1 ≤i ProofBy Theorem 2.5,GBiZ/2Z fori= 1,2,3 andG=GB1⊕GB2⊕GB3.Lets,t∈Gbe generators ofGBiandGBj, respectively, where 1 ≤i < j≤3.Thens?tis a symplectic automorphism of order 2 andp?1(Bi)∩p?1(Bj)?Fix(s?t).Since |G|=8, we get 2(Bi·Bj)=|p?1(Bi)∩p?1(Bj)|.Thus, we have that (Bi·Bj)≤4. By Lemma 3.13, the numerical class ofBis not one of (6.42), (6.120) of the list in Section 6. Lemma 3.14We assume that X/GP1×P1.Then B≠a1({q1}×P1)+a2({q2}×P1)+bC′+c(P1×{q3}), where C′is an irreducible curve, C′=(nC+mF)inPic(P1×P1), n,m>0,and a1a2,b,c are even integers. ProofWe assume thatB=a1({q1}×P1)+a2({q2}×P1)+bC′+c(P1×{q3}), whereC′is an irreducible curve,C′=(nC+mF),n,m>0, anda1a2,b,care even integers.By Theorem 2.5,G=G21,0⊕GC′.Bya1a2andbare even integers, the number of non-symplectic involution ofGis 2.Since (B0,1·C′) ≠ 0 and (B0,1·Bi1,0) ≠ 0 fori= 1,2 andcis an even integer,Gmust have at least 3 non-symplectic involutions.This is a contradiction. By Lemma 3.14, the numerical class ofBis not one of (6.43), (6.44)of the list in Section 6. Lemma 3.15We assume that X/GP1×P1.Then B≠a1({q1}×P1)+b1C1+b2C2+a2(P1×{q2}), where Ciis an irreducible curve, Ci=(niC+miF)inPic(P1×P1), ni,mi>0for i=1,2, and a1,a2,b1b2are even integers. ProofWe assume thatB=a1({q1}×P1)+b1C1+b2C2+a2(P1×{q2}), whereCiis an irreducible curve,C= (ni,mi) in Pic(P1×P1),ni,mi>0 fori= 1,2, anda1,a2,b1b2are even integers.By Theorem 2.5,G=GC1⊕GC2.Byb1b2is an even integer, the number of non-symplectic involutions ofGis at most 2.Since (B1,0·Ci) ≠ 0 and (B0,1·Ci) ≠ 0 fori= 1,2, anda1anda2are even integers,Gmust have at least 3 non-symplectic involutions.This is a contradiction. By Lemma 3.15, the numerical class ofBis not one of (6.47)–(6.52)of the list in Section 6. We assume that the numerical class ofBis (6.53) of the list in Section 6.We denoteBby 3B1,0+2B11,1+6B21,1+3B0,1.By Theorem 2.5,G11,1Z/2Z andG21,1Z/6Z andG=G11,1⊕G21,1.Then the number of subgroups of G which is generated by a non-symplectic automorphism of order 3 is 1.By Theorem 2.5 and (B1,0·B21,1) ≠ 0,Gmust have at least 2 such subgroups.This is a contradiction. We assume that the numerical class ofBis (6.54) of the list in Section 6.We denoteBby 3B1,0+3B11,1+3B21,1+3B0,1.By Theorem 2.5,Gi1,1Z/3Z fori=1,2, andG=G11,1⊕G21,1.Then the number of subgroups of G which is generated by a non-symplectic automorphism of order 3 is 3.By Theorem 2.5, (B1,0·Bi1,1) ≠ 0 and (B1,0·B0,1) ≠ 0,Gmust have at least 4 such subgroups.This is a contradiction. We assume that the numerical class ofBis (6.56) of the list in Section 6.We denoteBby 2B11,0+ 6B21,0+ 3B1,2+ 3B0,1.By Theorem 2.5,G11,0Z/2Z andG1,2Z/3Z, andG=G11,0⊕G1,2.Then the number of subgroups of G which is generated by a non-symplectic automorphism of order 3 is 1.By Theorem 2.5 and (B0,1·B1,2) ≠ 0,Gmust have at least 2 such subgroups.This is a contradiction. We assume that the numerical class ofBis (6.58) of the list in Section 6.We denoteBby 2B1,0+2B11,1+2B21,1+2B31,1+2B0,1.By Theorem 2.5,Gi1,1Z/2Z fori=1,2,3.Since(Bi1,1·Bj1,1) ≠ 0 for 1 ≤i < j≤3 andGi1,1Z/2Z fori= 1,2,3,G=G11,1⊕G21,1⊕G31,1.Then the number of non-symplectic involutions ofGis 4.Since (B1,0·B0,1)≠0,(B0,1·Ci)≠0 and (B1,0·Ci)≠0 fori=1,2,3,Gmust have at least 5 non-symplectic involutions.This is a contradiction. Lemma 3.16We assume that X/GP1×P1.If(P1×{qj}), where C′is an irreducible curve,{pi}×P1∩C′≠?, C∩P1×{qi}≠?, ai,c1,c2,b∈N≥2,then a1=a2and c1=c2. ProofLetCp1be one of irreducible components ofp?({p1} × P1).Since ({p1} × P1·{p1}×P1) = 0,Cp1is an elliptic curve.Letπ:X→Y:=X/GC′be the quotient map, andG′:=G/GC′be a finite Abelian subgroup of Aut(Y).Since {pi}×P1∩C≠?, the finite mapπ|Cp1:Cp1→C′p1:=π(Cp1) is a branched cover.SinceCp1is an elliptic curve,C′p1is P1Since the branch divisor of the quotient mapπ′:Y→Y/G′P1×P1is{qj}, the branch divisor ofπC′p1:C′p1→p1×P1isc1q1+c2q2.By Theorem 2.3, we get thatc1=c2.In the same way, we obtain thata1=a2. By Lemma 3.16, the numerical class ofBis not one of (6.61)–(6.64)of the list in Section 6. We assume that the numerical class ofBis one of (6.69)–(6.78) of the list in Section 6.By Theorem 2.3, there are an Abelian surface and a finite groupGsuch thatA/G=P1×P1and the branch divisor isB.By Theorem 2.2, there is a surjective morphism from aK3 surface to an Abelian surface.This is a contradiction. Lemma 3.17If X/GFnwhere n≥1, then B≠aC+bBs,t+cBu,v+dB0,1, where a,d≥0are even integers, a=0or a≥2, and b,c>0are even integers. ProofWe assume thatB=aC+bBs,t+cBu,v+dB0,1wherea,d≥0 are even integers,a= 0 ora≥2, andb,c >0 are even integers.By Theorem 2.5 and (Bs,t·Bu,v) ≠ 0, we get thatG=Gs,t⊕Gu,v.Then the number of non-symplectic involution ofGis 2.Since(Bs,t·B0,1)≠0 and (Bu,v·B0,1)≠0,Gmust have at least 3 non-symplectic involutions.This is a contradiction. By Lemma 3.17, the numerical class ofBis not one of (6.104), (6.114), (6.115), (6.118),(6.141), (6.148), (6.184), (6.185), (6.187), (6.232), (6.234), (6.245), (6.246), (6.259), (6.291) of the list in Section 6. Lemma 3.18For the branch divisorwe get thatis an even integerfor1 ≤i≤k. ProofFori=1,···,k,we putwhereCjis a smooth curve forj=1,···,l.By Theorem 2.5,C1,···,Clare pairwise disjoint.Then we get thatSinceXis aK3 surface, (Cj·Cj) is an even integer, and henceis an even integer. By Lemma 3.18, the numerical class ofBis not one of (6.106), (6.107), (6.140), (6.147),(6.180), (6.183), (6.231), (6.233), (6.258) of the list in Section 6. We assume that the numerical class ofBis (6.110) of the list in Section 6.We denoteBby 2B1,2+4B11,1+4B21,1+2B0,1.By Theorem 2.5,G1,2Z/2Z andGi1,1Z/4Z fori= 1,2 Since (B1,2·Bi1,1) ≠ 0 fori= 1,2, by Theorem 2.5,G=G1,2⊕G11,1⊕G21,1, and hence |G| = 36.Lets∈G1,2andt∈G11,1be generators.Thens?tis a non-symplectic automorphism of order 4 andp?1(B1,2)∩p?1(B11,1)?Fix(s?t).SinceG=G1,2⊕G11,1⊕G21,1andB= 2B1,2+4B11,1+4B21,1+2B0,1, by Theorem 2.5, Fix(s?t) does not contain a curve.By [2, Proposition 1], the number of isolated points of Fix(s?t) is 4.Since (B1,2·B11,1) = 2,we get that |p?1(B1,2)·p?1(B11,1)|≥8.This is a contradiction. We assume that the numerical class ofBis (6.121) of the list in Section 6.We denoteBby 2B2,3+2B11,1+2B21,1+2B0,1.By Theorem 2.5,G2,3G11,1G21,1Z/2Z.Since an intersection of two ofB2,3,B11,1,B21,1is not an empty set,by Theorem 2.5,G=G2,3⊕G11,1⊕G21,1,and hence |G| = 8.Lets∈G2,3andt∈G0,1be generators.Sincesandtare non-symplectic involutions, Fix(s) and Fix(t) are sets of curves and Fix(s?t) is a set of 8 isolated points.Since (B2,3·B0,1) = 2, |p?1(B2,3)∩p?1(B11,1)| = 4.Since Fix(s?t) ?p?1(B2,3)∩p?1(B0,1),X/(G2,3⊕G0,1) has 2 singular points, however, since the branch divisor of the double coverX/(G2,3⊕G0,1) →X/Gis 2B11,1+2B21,1and (B11,1·B21,1) = 1, the number of singular points ofX/(G2,3⊕G0,1) must be 1.This is a contradiction. As for the case of (6.121), the numerical class ofBis not one of (6.191)–(6.192) of the list in Section 6. We assume that the numerical class ofBis (6.123) of the list in Section 6.We denoteBby 2B2,2+2B1,2+2B1,1+2B0,1.By Theorem 2.5,G2,2G1,2G1,1Z/2Z.Since an intersection of two ofB2,2,B1,2,B1,1is not an empty set,by Theorem 2.5,G=G2,2⊕G1,2⊕G1,1.Since(B2,2·B1,2)=4,X/(G2,2⊕G1,2)is smooth.Then there is a double coverX/G2,2⊕G1,2→X/GF1whose branch divisor is 2B1,1+2B0,1.Since?Pic(F1), by Theorem 3.1,this is a contradiction. We assume that the numerical class ofBis (6.125) of the list in Section 6.We denoteBby 2B11,2+ 2B21,2+ 2B11,1+ 2B21,1.By Theorem 2.5,Gi1,2Gi1,1Z/2Z fori= 1,2.Since an intersection of two ofB11,2,B21,2,B11,1,B21,1is not an empty set, by Theorem 2.5,G= G11,2⊕G21,2⊕G11,1⊕G21,1orG=G11,2⊕G21,2⊕G11,1.We assume thatG=G11,2⊕G21,2⊕G11,1⊕G21,1.Since |G| = 16 and (B11,2·B21,2) = 3, |p?1(B11,2∩B21,2)| ≥12.Since the number of isolated points of symplectic involution is 8, this is a contradiction.Therefore,G=G11,2⊕G21,2⊕G11,1. By Theorem 3.1, there are the Galois coversp1:Y1→F1andp2:Y2→F1such that the branch divisor ofp1is 2B11,2+2B21,2and that ofp2is 2B11,1+2B21,1.LetX′:=Y1×F1Y2.Then there is the Galois coverq:X′→F1whose branch divisor is 2B11,2+2B21,2+2B11,1+2B21,1and Galois group is isomorphic to Z/2Z⊕2as a group.By Theorem 2.1, there is a symplectic automorphism of order 2,s∈Gsuch thatX′=X/〈s〉.Sincesis symplectic, the minimal resolutionf:X′m→X′is aK3 surface.Lete1,···,e8be the exceptional divisors off.We set {p1,p2,p3} :=B11,2∩B21,2and {p4} :=B11,1∩B21,1.Letπ: Blow{p1,p2,p3,p4}F1→F1be the blow-up of P1×P1at pointsp1,p2,p3,p4, andEi:=π?1(pi) be an exceptional divisor ofπfori= 1,2,3,4.Since the support ofBis simple normal crossing, in the same way of Proposition 3.6, there is a Galois coverq:X′m→Blow{p1,p2,p3,p4}F1whose branch divisor is 2C11,2+2C21,2+2C11,1+2C21,1and Galois group is isomorphic to Z/2Z⊕2as a group, whereC11,2,C21,2,C11,1,C21,1are proper transforms ofB11,2,B21,2,B11,1,B21,1by the birational mapπ?1in order.Notice thatand there is the commutative diagram: Furthermore, we put {x1,···,x8} := Fix(s).Then Blow{x1,···,x8}X/〈s〉 =X′m, the branch divisor of the double cover Blow{x1,···,x8}X→X′mis, and there is the commutative diagram: In the same way of Proposition 3.6, we get that Since Blow{x1,···,x8}XandX′mare smooth, andwe get thatPix(X′m), and hence SinceC11,2∩C21,2is an empty set andby Theorem 3.1,there is the Galois coverg:Z→Blow{p1,p2,p3,p4}F1such thatZis smooth, the branch divisor is 2C11,2+2C21,2,and the Galois group is isomorphic to Z/2Z as a group.By Theorem 2.1,there is a non-symplectic automorphism of order 2ρofX′msuch thatX′m/〈ρ〉=Z.Leth:X′m→Zbe the quotient map.Thenq=g?h, and hence∈Pic(X′m)ρ.Since the degree ofgis 2 andwe get thatg??Pic(Z).Recall thatCi1,1=C+F?e4in Pic(Blow{p1,p2,p3,p4}F1) fori= 1,2.Since the branch divisor ofhis 2g?C11,1+ 2g?C21,1,we get thatBy [2], Pic(X′m)ρis generated byh?Pic(Z) andover Z.Sinceandwe may assume that there isα∈Pic(Z) such that We assume that the numerical class ofBis (6.126) of the list in Section 6.We denoteBby 2B1,2+2B11,1+2B21,1+2B31,1+2B0,1.By Theorem 2.5,G1,2Gi1,1G0,1Z/2Z wherei= 1,2,3.Since an intersection of two ofB1,2,B11,1,B21,1,B31,1,B0,1is not an empty set, by Theorem 2.5,G=G1,2⊕G11,1⊕G21,1⊕G31,1.LetGsbe the subgroup ofGwhich consists of symplectic automorphisms ofG.ThenGsZ/2Z⊕3.By [16], the number of singular points ofX/Gsis 14, however, since the branch divisor of the double coverX/Gs→X/GisB= 2B1,2+2B11,1+2B21,1+2B31,1+2B0,1and the support ofBis simple normal crossing,the number of singular points ofX/Gsis 13.This is a contradiction.Therefore, the numerical class ofBis not (6.126) of the list in Section 6. Lemma 3.19If X/GFnwhere n≥1, then B≠aC+bBs,t+cBu,vwhere a,b,c>0are even integers, and(C·Bs,t)≠0and(C·Bu,v)≠0, i.e., s≠t or u≠v. ProofWe assume thatB=aC+bBs,t+cBu,vwherea,b,c >0 are even integers, and(C·Bs,t)≠0 and (C·Bu,v)≠0 By Theorem 2.5 and (Bs,t·Bu,v)≠0,G=Gs,t⊕Gu,v.Then the number of non-symplectic involutions ofGis 2.Since (C·Bs,t)≠0 and (C·Bu,v)≠0,Gmust have at least 3 non-symplectic involutions.This is a contradiction. By Lemma 3.19, the numerical class ofBis not one of (6.139), (6.181), (6.182), (6.244) of the list in Section 6. We assume that the numerical class ofBis (6.189) of the list in Section 6.We denoteBby 2B1,0+2B1,4+2B11,1+2B21,1.By Theorem 2.5,wherei=1,2.Since (B1,4·Bi1,1)≠0 fori=1,2, by Theorem 2.5,G=G1,4⊕G11,1⊕G21,1.Lets∈G11,1andt∈G21,1be generators.Since the number of non-symplectic automorphisms of order 2 ofGis 4 and Theorem 2.5, we may assume that Fix(s) is the support ofp?B11,1.Since the support ofBis simple normal crossing and (B1,4·B11,1) = 4,X/(G1,4⊕G11,1) is smooth.Then there is the Galois coverX/G1,4⊕G11,1→F1such that the branch divisor is 2B1,0+2B21,1and the Galois group is isomorphic to Z/2Z as a group.Sincethis is a contradiction. As for the case of (6.189), the numerical class ofBdoes not (6.190)of the list in Section 6. We assume that the numerical class ofBis (6.228)of the list in Section 6.We denoteBby 3B1,0+3B1,2+3B1,4.By Theorem 2.5 and (B1,2·B1,4)≠0,G=G1,2⊕G1,4.Lets∈G1,4be a generator ofG1,4.Then the only curve of Fix(s) isC1,4.Since (B1,4·B1,4) = 6, the genus ofC1,4is 4.By [1,14], Fix(s) does not have isolated points, and henceX/G1,4is smooth.Letq:X/G1,4→X/Gbe the quotient map.Then the degree ofqis 3, and the branch divisor ofqis 3B1,0+3B1,2.Since the degree ofqis 3 andX/G1,4is smooth,332(B1,0·B1,0) is an integer.Since (B1,0·B1,0)=?2,This is a contradiction. We assume that the numerical class ofBis (6.229) of the list in Section 6.We denoteBby 3B1,0+3B1,2+3B1,3+3B0,1.By Theorem 2.5,Since (B1,2·B1,3) ≠ 0, by Theorem 2.5,G=G1,2⊕G1,3.Lets,t∈Gbe generators ofG1,2andG1,3respectively such thats?tis a non-symplectic automorphism of order 3.SinceG=G1,2⊕G1,3, the number of subgroups ofGwhich are generated by a non-symplectic automorphism of order 3 is 3.Since (B1,2·B0,1) ≠ 0 and (B1,3·B0,1) ≠ 0, we get thatp?1(B0,1) is contained in Fix(s?t), and hencep?1B1,0is contained in Fix(s).Since |G| = 9,there is an elliptic curveC0,1onXsuch thatp?B0,1= 3C0,1.By [1,14], the number of isolated points of Fix(s?t) is 3.Since (B1,0·B1,3) = 1 and (B1,2·B1,3) = 3, we have|p?1(B1,0∪B1,2)∩p?1(B1,3)| = 4.Sincep?1(B1,0∪B1,2) ?Fix(s) andp?1(B1,3) ?Fix(t),we get thatp?1(B1,0∪B1,2)∩p?1(B1,3)?Fix(s?t).By the fact that the number of isolated points of Fix(s?t) is 3, this is a contradiction. We assume that the numerical class ofBis (6.243) of the list in Section 6.We denoteBby 2B1,0+2B1,4+2B2,4.By Theorem 2.5,G=G1,4⊕G2,4.Lets∈Gbe a generator ofG1,4.Since (B1,0·B1,4) ≠ 0 and (B1,4·B2,4) ≠ 0, the only curve of Fix(s) isC1,4.Since the fixed locus of a non-symplectic involution does not have isolated points,X/G1,4is smooth.Letq:X/G1,4→X/GF2be the quotient map.The degree ofqis 2 and the branch divisor ofqis 2B1,0+2B2,2.Sinceby Theorem 3.1, this is a contradiction. We assume that the numerical class ofBis (6.249) of the list in Section 6.We denoteBby 2B1,0+2B11,3+2B21,3+2B1,2.By Theorem 2.5,Gi1,3G1,2Z/2Z wherei= 1,2.Since an intersection of two ofB11,3,B21,3,B1,2is not an empty set,G=G11,3⊕G21,3⊕G1,2.Since|G|=8 and (B11,3·B21,3)=4,Y:=X/(G11,3⊕G21,3) is smooth.Then there is the Galois coverq:Y→X/Gsuch that the branch divisor is 2B1,0+2B1,2, and the Galois group is Z/2Z as a group.Since the fixed locus of a non-symplectic automorphism of order 2 does not have isolated points,X/G11,3is smooth, and there is the Galois coverq′′:X/G11,3→Ysuch that the branch divisor ofq′′is 2q?B11,3and the Galois group ofq′′is Z/2Z as a group.SinceYandX/G11,3are smooth, and the degree ofq′′is two, we get thatRecall that the branch divisor ofqis 2B1,0+2B1,2, and the degree ofqis two.Sincewe get thatSince (B1,0·F)=1, we get thatSincethis is a contradiction.Therefore, the numerical class ofBis not (6.249). We assume that the numerical class ofBis (6.250) of the list in Section 6.We denoteBby 2B1,0+2B1,3+2B11,2+2B21,2+2B0,1.By Theorem 2.5,G1,3Gi1,2Z/2Z wherei= 1,2.Since an intersection of two ofB1,3,B11,2,B21,2is not an empty set, by Theorem 2.5,G=G1,3⊕G11,2⊕G21,2.Lets∈G11,2be a generator.Since the number of non-symplectic automorphisms of order 2 ofGis 4 and Theorem 2.5, we may assume thatp?1(B11,3) andp?1(B1,0) are contained in Fix(s).Since the support ofBis simple normal crossing and (B1,3·B1,0+B11,2)=4,X/(G1,3⊕G11,2)is smooth and there is the Galois coverX/(G1,3⊕G11,2)→F2such that the branch divisor is 2B21,2+2B0,1and the Galois group is Z/2Z as a group.Sincethis is a contradiction. We assume that the numerical class ofBis (6.286) of the list in Section 6.We denoteBby 2B1,0+3B11,4+6B21,4.By Theorem 2.5,G1,0Z/2Z,G11,4Z/3Z,G21,4Z/6Z andG=G11,4⊕G21,4.Letsbe a generator ofG11,4.Since (B11,4·B11,4) = 4, the genus ofC11,4is 5 wherep?B11,4= 3C11,4.SinceG1,0Z/2Z and (B11,4·B21,4) ≠ 0, the only curve of Fix(s) isC11,4.By [1,14], this is a contradiction. We assume that the numerical class ofBis (6.287) of the list in Section 6.We denoteBby 2B1,0+4B11,4+4B21,4.By Theorem 2.5,Gi1,4Z/4Z fori= 1,2.Since (B11,4·B21,4) ≠ 0,by Theorem 2.5,G=G11,4⊕G21,4.Lets∈G11,4andt∈G21,4be generators.Then nonsymplectic involutions ofGares2andt2.By Theorem 2.5, we may assume that Fix(s2) =p?1(B1,0)∪p?1(B11,4) and Fix(t2)=p?1(B21,4).For a symplectic involutions2?t2, sinceX/Gis smooth, Fix(s2?t2) ?Fix(s2)∩Fix(t2).Since (C·Bi1,4) = 0 and (B11,4·B11,4) = 4, we get thatp?1(B1,0∪B11,4)∩p?1(B21,4) are 4 points.By the fact that the fixed locus of a symplectic involution of aK3 surface are 8 isolated points, this is a contradiction. We assume that the numerical class ofBis (6.305)of the list in Section 6.We denoteBby 3B1,0+2B11,6+6B21,6.By Theorem 2.5 and (B11,6·B21,6)≠0,G=G11,6⊕G21,6.Letρ1,ρ2∈Gbe generators ofGB11,6andGB21,6, respectively.Thenρ22is a non-symplectic automorphism of order 3 and a generator ofG1,0.Since (C·C) = ?6 and |G| = 12, we get thatwhereCjis a smooth rational curve.ThenC1,···,C4,C21,6?Fix(ρ22) wherep?B21,6= 6C21,6.By [1,14], this is a contradiction. We assume that the type ofBis(6.45)of the list in Section 6.We denoteBby 4B11,0+4B21,0+2B1,3+2B0,1.We take the Galois coverq:P1×P1→P1×P1whose branch divisor is 4B11,0+4B21,0.Since the support ofBis simple normal crossing,q?(2B1,3+2B0,1) = 2B4,3+2B0,1.By Theorem 2.2, there is the Galois morphismg:X→P1×P1such that the branch divisor is 2B4,3+2B0,1and the Galois group is Abelian.Since the numerical class of 2B4,3+2B0,1is(6.25), this is a contradiction. As for the case of(6.45), the numerical class ofBis not one of (6.46), (6.55), (6.57), (6.59),(6.60), (6.65), (6.66), (6.67), (6.68), (6.102), (6.105), (6.108), (6.111), (6.116), (6.124), (6.136),(6.138), (6.142), (6.144, (6.149), (6.153), (6.178), (6.186), (6.221), (6.222), (6.226), (6.260),(6.267) of the list in Section 6 by (6.25), (6.24), (6.27), (6.25), (6.37), (6.34), (6.40), (6.34),(6.34), (6.212), (6.213), (6.214), (6.215), (6.216), (6.217), (6.286), (6.286), (6.287), (6.287),(6.305), (6.228), (6.241), (6.243), (6.286), (6.287), (6.303), (6.305), (6.308) in order. Therefore, we get Theorem 1.5. In this section, first of all, we will show Theorems 1.1–1.2.Next, we will show Theorem 1.4.By Section 3, we had that ifX/Gis P2or Fn, thenGis one of AGas a group. Proposition 4.1Let X be a K3surface and G be a finite subgroup ofAut(X)such that X/G is a smooth rational surface.For a birational morphism f:X/G→Fn, we get that0 ≤n≤12. ProofLetf:X/G→Fnbe a birational morphism,eibe the exceptional divisors fori=1,···,m, andbe the branch divisor.SinceX/Gand Fnare smooth andfis a birational morphism, we getand there are positive integersaifori=1,···,msuch thatBy Theorem 2.4, where (ci,di) = (1,0), (0,1), ordi≥cin >0.SinceKFn= ?2C?(n+2)Fin Pic(Fn), by Theorem 2.4, we get thatIn the same way as Proposition 3.1, we get this proposition. LetXbe aK3 surface,Gbe a finite subgroup of Aut(X) such thatX/Gis smooth, andf:X/G→Fnbe a birational morphism.By Proposition 4.1, we get 0 ≤n≤12.By the proof of Proposition 4.1, the numerical class off?Bis one of the list on Section 3.LetwhereBiis not an exceptional divisor offfori= 1,···,kandBjis an exceptional divisor offforj=k+1,···,l.Sinceis isomorphic toandf(Bj) is a point forj=k+1,···l,is simply connected.By Theorem 2.5,Gis generated byG1,···,Gk.Therefore,as for the case of Hirzebruch surface,we will guessGfrom the numerical class off?B.Recall that ifGis Abelian, thenGiis a cyclic group, which is generated by a purely non-symplectic automorphism of orderbi.Iff?B1=C,orF, thenGis generated byG2,···,Gk, and if (f?B1,f?B2)=(C,F), thenGis generated byG3,···,Gk. Recall that sinceX/Gis a smooth rational,X/Gis given by blowups of Fn.Next, we will investigate the relationship between a branch divisor and exceptional divisors of blow-ups. Lemma 4.1Let X be a K3surface, and G?Aut(X)a finite subgroup such that X/G is a smooth rational surface, and B be the branch divisor of the quotient map p:X→X/G.For a birational morphism h:X/G→T where T is a smooth projective surface, let eibe the exceptional divisor of h for i= 1,···,m.Then for i= 1,···,m we have that h(ei) ∈Supp(h?B). ProofLete1,···,embe the exceptional divisors ofh.SinceX/GandTare smooth andhis birational,and there are positive integersaisuch that We assume thath(ei) ?Supp(h?B) for some 1 ≤i≤m.For simply, we assume thati= 1,i.e.,h(e1) ?Supp(h?B).LetB1,···,Bkbe irreducible components ofBsuch thatBjis not an exceptional divisor ofhforj= 1,···,k.Sinceh(e1) ?Supp(h?B), there are integerscj,ssuch thatwhereCjis an irreducible curve inT.By Theorem 2.4, we get that wherelj= 0 orfor some an integerdj≥2.Sinceai≥1,cj,1= 0,lj≥0 and, this is a contradiction. Proposition 4.2Let X be a K3surface, G?Aut(X)be a finite subgroup such that the quotient space X/G is smooth, and B be the branch divisor of the quotient morphism p:X→X/G.Let f:X/G→T be a birational morphism where T is a smooth surface, e1,···,embe the exceptional divisors of f, andis an irreducible curves on U fori= 1,···,u.Ifis smooth for each1 ≤i≤u, then for1 ≤j≤m there are1 ≤s < t≤usuch that ProofWe setwhereBiis not an exceptional divisor offfori=1,···,u, andBjis an exceptional divisor offforj=u+1,···,k.ThenWe assume thatf?Biis a smooth curve fori=1,···,u.By Lemma 4.1,f(ei)∈supp(f?B)fori=1,···,m. LetS:=X/G,Z:={f(e1),···,f(em)}:={z1,···,zv}?Twhere be the blow-up, andEi:=q?1(zi) be the exceptional divisor ofqfor 1 ≤i≤v.Then there is a birational morphismg:S→BlowZTsuch thatf=q?g, i.e., the following diagram is commutative: By changing the number if necessary, we assume thatg(ei) =Eifor 1 ≤i≤v.Then the exceptional divisors ofgareev+1,···,em.Since Pic(BlowZT)=q?Pic(T)andf=q?g, wherea′iis a positive integer fori=v+1,···,m. We assume that for some 1 ≤i≤m,f(ei) ?f?Bs∩f?Btfor each 1 ≤s < t≤u.SinceZ= {f(e1),···,f(ev)}, we assume that 1 ≤i≤v.For simplicity, we assume thati= 1.In addition, sincef(ej) ∈supp(f?B) forj= 1,···,m, by changing the number if necessary,we assume thatf(e1) ∈supp(f?B1), andf(e1) ?supp(f?Bj) for 2 ≤j≤u.Recall that the exceptional divisors ofqareE1,···,Ev, the exceptional divisors ofgareev+1,···,em, andg(ei) =Eifor 1 ≤i≤v.Sincef=q?g, forj= 1,···,uthere are non-negative integerscj,s,c′j,tsuch that Sincef(e1) ?f?Bjfor 2 ≤j≤u, we get thatcj,1= 0 for 2 ≤j≤u.Sincef?B1is smooth,c1,1=1.Since From the coefficient ofg?E1, we get thatSinceb1≥2, this is a contradiction. LetXbe aK3 surface,Gbe a finite subgroup of Aut(X)such thatX/Gis a smooth rational surface,andBbe the branch divisor of the quotient mapp:X→X/G.Leth:X/G→Tbe a birational morphism whereTis a smooth projective surface, ande1,···,embe the exceptional divisors ofh.We setWe writesuch thath?Bi=B′ifori= 1,···,l.ThenBjis one of the exceptional divisor ofhforj=l+1,···,k, and fori=1,···,lthere are non-negative integersci,1,···,ci,msuch that Remark 4.1In the above situation,foreuandevwhere 1 ≤u Remark 4.2In the situation of Proposition 4.2, we assume thatT= Fn.Then there are positive integersa1,···,amsuch thatBy the proof of Proposition 4.2, we get thata1=···=au=1 and whereβi= 1 ifeiis not an irreducible component ofB, andβiis the ramification index ateiifeiis an irreducible component ofB. Furthermore, we assume thatX/G≠ Blow{h(e1),···,h(eu)}Fn.For the birational morphismg:X/G→Blow{h(e1),···,h(eu)}Fnin the proof of Proposition 4.2, we rearrange the order so that {g(eu+1),···,g(eu+v)} = {g(eu+1),···,g(em)}, wherev:= |{g(eu+1),···,g(em)}|.Like the proof of Proposition 4.2, by considering the blow-up of Blow{h(e1),···,h(eu)}Fnat{g(eu+1),···,g(eu+v)}, we get thatau+1=···=au+v=2 and whereβi= 1 ifeiis not an irreducible component ofB, andβiis the ramification index ateiifeiis an irreducible component ofB. Recall that by Theorem 2.5,GBiis generated by a non-symplectic automorphism of orderbi.As a corollary of Theorem 2.5 and Proposition 4.2, we get the following Theorem 4.1. Theorem 4.1Let X be a K3surface, G be a finite subgroup ofAut(X)such that X/G is smooth, and B be the branch divisor of the quotient map p:X→X/G.Let f:X→S be the birational morphism where S is minimal rational surface.We putwhere Biisan irreducible curve for i= 1,···,k.We denote by Gsthe subgroup of G, which consists of symplectic automorphisms of G, and b the least common multiple of b1,···,bk.Then there is a purely non-symplectic automorphism g∈G of order b such that G is the semidirect product Gs〈g〉of Gsand〈g〉. ProofSinceGsis a normal subgroup ofGandG/Gsis a cyclic group, in order to show Theorem 4.1, we only show that there is a purely non-symplectic automorphismg∈Gof orderb. First of all, we assume thatX/GP2.We putwhereBiis an irreducible curve fori= 1,···,k.By Theorem 2.4,degBi+degKP2, in whichKP2is the canonical line bundle of P2.Since the degree ofKP2is ?3 andfor any positive integerl, we get thatIfthenb1=···=bk=2.By Theorem 2.5, in this case the statement of theorem is established.We assume thatBy[15, Theorem 2],b=bifor some 1 ≤i≤korb=l.c.m(bi,bj) fori < j.By Theorem 2.5, in the former case, we get this theorem. For the latter, i.e., ifb≠bifor 1 ≤i≤k, thenBis one of(i) 3L1+3L2+3L3+2L4+2L5,whereL3passes through the pointsL1∩L2andL4∩L5(see[15,pp.408]),(ii)3L1+3L2+3L3+2Q,whereL1,L2are the tangent toQandL3is in general position with respect toL1∪L2∪Q(see [15, pp.408]), and (iii) 2L1+2L2+3L3+3Q, whereL1,L2,L3are three distinct tangent lines toQ(see [15, pp.410]).Here,LiandQare smooth curves on P2with degLi= 1 and degQ=2 fori=1,···,5.Then there are 1 ≤i Next, we assume thatX/GFn.By the list of the numerical class ofBin Section 6, if the numerical class ofBis not one of (6.65), (6.70), (6.73), (6.77), (6.83), (6.92), (6.102), (6.127),(6.128), (6.132), (6.136), (6.143), (6.153), (6.154), (6.170), (6.235), (6.251), (6.252), (6.253),thenb=bifor some 1 ≤i≤k.Therefore,by Theorem 2.5,we get this theorem.If the numerical class ofBis one of(6.65),(6.70),(6.73),(6.77),(6.92),(6.127),(6.128),(6.132),(6.136),(6.143),(6.153), (6.154), (6.170), (6.235), (6.251), (6.252), (6.253), then there are 1 ≤i < j≤ksuch thatb=l.c.m(bi,bj),Bi+Bjis simple normal crossing,andis not an empty set.As for the case of P2, we get this theorem. We assume that the numerical class ofBis (6.83).We writeB= 3B3,3+2B10,1+2B20,1.SinceB10,1∩B20,1is an empty set, ifB3,3∩B10,1is not one point, then by(B3,3·B10,1)=3, there is a pointy∈B3,3∩B10,1such that the support ofBis simple normal crossing aty.Sinceb=6,by Theorem 2.5, we get this theorem.Therefore, we assume thatB3,3∩B10,1andB3,3∩B20,1are one point.Letq:X/Gs→X/Gbe the quotient map.Then the singular locus ofX/Gsisq?1(B3,3∩B10,1)∪q?1(B3,3∩B20,1).Since the Galois group ofqisG/GsZ/6Z, the branch divisor ofqisB, andB3,3∩B10,1andB3,3∩B20,1are one point,X/Gshas just two singular point.By [16, Theorem 3], this is a contradiction.Therefore, if the numerical class ofBis(6.83), then we get this theorem.As for the case of (6.83), we get this theorem for (6.102). Finally,we assume thatX/Gis not P2or Fn.We take a birational morphismf:X/G→Fnwhere 0 ≤n.Lete1,···,embe the exceptional divisors off.In the same way of the case whereX/GP2or Fn, we only consider the case that the numerical class off?Bis one of (6.65),(6.70), (6.73), (6.77), (6.83), (6.92), (6.102), (6.127), (6.128), (6.132), (6.136), (6.143), (6.153),(6.154), (6.170), (6.235), (6.251), (6.252), (6.253). We assume that the numerical class off?Bis (6.65).By Remark 4.2, there are positive integersa1,···,a5,bsuch that Since the numerical class off?Bis (6.65), we may assume thata1ora2is 0, and eithera4ora5is 0.However, there are not such positive integers.Therefore, the numerical class off?Bis not (6.65).As for the case of (6.65), the numerical class ofBis not one of (6.73), (6.77),(6.128), (6.132), (6.170), (6.235), (6.251), (6.253). We assume that the numerical class off?Bis (6.70).By Remark 4.2, there are positive integersa1,···,a6,bsuch that Since the numerical class off?Bis (6.70), we may assume that two ofa1,a2anda3are 0, and two ofa4,a5anda6are 0.The integers satisfying the above conditions is only(a1,···,a6,b)=(1,0,0,1,0,0,12).Therefore, forfor some 1 ≤i≤l.By Theorem 2.5,if the numerical class off?Bis (6.65), then we get this theorem.As for the case of (6.70), if the numerical class ofBis one of (6.136), (6.143), then we get this theorem. We assume that the numerical class ofBis(6.83).By Remark 4.2,there are positive integersa1,···,a6,bsuch that Since the numerical class off?Bis(6.83),we may assume that eithera2ora3is 0.The integers satisfying the above conditions is (a1,a2,a3,b) = (2,1,0,6) or (2,0,1,6).Therefore, we get this of theorem.As for the case of (6.83), if the numerical class ofBis one of (6.92), (6.102),(6.127), (6.153), (6.154), (6.252), then we get this theorem. Theorem 4.2Let X be a K3surface and G be a finite subgroup ofAut(X)such that X/G is smooth.For a birational morphism f:X/G→Fnwhere0 ≤n, we get that n is not one of5,7,9,10,11. ProofLetp:X→X/Gbe the quotient map, andbe the branch divisor ofp.Letf:X/G→Fnbe a birational morphism where 0 ≤n, ande1,···,embe the exceptional divisors off. First we will show this theorem for the cases wherefis an isomorphism, i.e.,X/GFn.By Theorem 2.4,n= 0,1,2,3,4,5,6,7,8,9 or 12.We assume thatn= 5,7 or 9.Then the numerical class ofBis one of(6.296),(6.297),(6.298),(6.299),(6.300),(6.301),(6.310),(6.314),(6.315) of the list in Section 6. We assume that the numerical class ofBis (6.296).We denoteBby 4B1,0+2B1,5+4B1,6.LetwhereCiis a smooth curve fori= 1,···,m.Since (B1,0·B1,0)<0,(Ci·Ci)<0.SinceXis aK3 surface, andCiis irreducible, we get that (Ci·Ci)=?2.Since the degree ofpis |G| and (B1,0·B1,0) = ?5, we get thatand hencewhereC′jis a smooth curve forj= 1,···,l.SinceSincewe get thatBywe get that the numerical class ofBis not (6.296).As for the case of (6.296), the numerical class off?Bis not one of (6.297), (6.298), (6.299), (6.300), (6.301),(6.310), (6.314), (6.315).Therefore, ifX/GFn, thenn≠5,7,9,10,11. Next, we assume thatfis not an isomorphism, i.e.,X/Gis not a Hirzebruch surface Fn.By the proof of Proposition 4.1, the numerical class off?Bis one of the list in Section 6.As a result,n= 0,1,2,3,4,5,6,7,8,9 or 12.We assume thatn= 5,7 or 9.The numerical class off?Bis one of (6.296), (6.297), (6.298), (6.299), (6.300), (6.301), (6.310), (6.314), (6.315). We assume that the numerical class off?Bis (6.296).LetwhereCiis a smooth curve fori= 1,···,m.Since the degree ofpis |G|, by (C·F) = 1, we get that|G| = 4m(C1·p?f?F), and hence |G| is a multiple of 4m.Sincef?B1,0=C, (B1,0,B1,0) ≤(C·C)=?5.Bywe get thatSince the numerical class off?Bis (6.296), there must be positive integersa1,a2,a3,bsuch that and eithera1ora2is 0.The integers satisfying the above conditions are only (a1,a2,a3,b) =(1,0,1,2), and hencef(ei)∈f?B1,5∩f?B1,6for eachi=1,···,l.Since (f?B1,5·f?B1,6)=1,f?B1,5∩f?B1,6is one point.We putx:=f?B1,5∩f?B1,6.Letq:BlowxF5→F5be the blow-up of F5atx.Then there is a birational morphismg:X/G→BlowxF5such thatf=q?g.LetC′:=g?B1,0.LetEbe the exceptional divisor ofq.Sincef(ei) =xfor eachi= 1,···,l,g(ei) ∈Efor eachi= 1,···,l.Sinceg?B= 4C′+2g?B1,5+4g?B1,6+2E, ifgis not an isomorphism, then there must be integersa1,a2,a3,a4,bsuch that and ifa1is not 0, then eithera2=a3= 0.However, there are not such positive integers.Therefore,gis an isomorphism,i.e.,X/G=BlowxF5,and henceB=4B1,0+2B1,5+4B1,6+2Eand (B1,0·E)=1.We putwhereC′jis a smooth curve forj=1,···,u.SinceThis is a contradiction.Therefore, the numerical class ofBis not (6.296).As for the case of (6.296), the numerical class ofBis not one of (6.310), (6.314). We assume that the numerical class off?Bis(6.297).Then there must be integersa1,a2,a3,a4,bsuch that and ifa1is not zero, thena2=a3= 0.The integers satisfying the above condition is(a1,a2,a3,a4,b) = (1,0,0,1,2) or (0,0,1,1,2).Therefore, for eachi= 1,···,l, we get thatf(ei)∈f?B1,0∩f?B0,1orf(ei)∈f?B21,5∩f?B0,1.Iff(ei)∈f?B21,5∩f?B0,1for alli=1,···,l,then (B1,0·B1,0)=?5 and(B1,0·B0,1)=1.However,as for the case ofX/GFn, we can see that such things can not happen.Therefore,f(ei)∈f?B1,0∩f?B0,1for somei=1,···,l.By using the blow-up of F5atx:=f?B1,0∩f?B0,1,as for the case of(6.296),this is a contradiction.Therefore, the numerical class ofBis not (6.297).As for the case of (6.297), the numerical class ofBis not (6.315). We assume that the numerical class off?Bis(6.298).Then there must be integersa1,a2,a3,bsuch that The integers satisfying the above condition are only(a1,a2,a3,b)=(1,0,1,2),and hencef(ei)∈f?B1,5∩f?B1,6for eachi=1,···,l.Since (f?B1,5·f?B1,6)=1,f?B1,5∩f?B1,6is one point.We putx:=f?B1,5∩f?B1,6.Letq:BlowxF5→F5be the blow-up of F5atx.As for the case of (6.296), since there are no integersa1,a2,a3,a4,bsuch that we get thatX/G= BlowxF5, and henceB= 6B1,0+2B1,6+3B1,6+2E, and (B1,0·E) = 1.We putwhereC′jis a smooth curve forj= 1,···,u.Since (E·E) = ?1, we get thatu=and henceSinceis a multiple ofu.This is a contradiction.Therefore, the numerical class ofBis not (6.298). We assume that the numerical class off?Bis (6.299).Then there must be positive integersa1,a2,a3,a4,bsuch that anda1a3= 0.The integers satisfying the above conditions are (a1,a2,a3,a4,b)= (1,0,0,1,2)or (0,1,1,1,6).Therefore, for eachi=1,···,l, we get thatf(ei)∈f?B1,0∩f?B0,1orf(ei)∈f?B1,6∩f?B1,5∩f?B0,1.Iff(ei)∈f?B1,6∩f?B1,5∩f?B0,1for alli=1,···,l,then(B1,0·B1,0)=?5 and (B1,0·B0,1)=1.We get that this is not established in the same way as in the case ofX/GFn.By using the blow-up of F5atx:=f?B1,0∩f?B0,1, as for the case of (6.298), we get that there is no case wheref(ei) ∈f?B1,0∩f?B0,1for somei= 1,···,l.Therefore, the numerical class ofBis not (6.299).As for the case of (6.299), the numerical class ofBis not one of (6.300)–(6.301). Corollary 4.1Let X be a K3surface and G be a finite subgroup ofAut(X)such that X/G is smooth.If there is a birational morphism f:X/G→Fnfrom the quotient space X/G to a Hirzebruch surfaceFnwhere n= 6,8or12, then f is an isomorphism, i.e., X/G is a Hirzebruch surface. ProofLetn≥1 andC?n?Fnbe the unique irreducible curve such that(C?n·C?n)=?n.Since forx∈Fn, ifx∈C?n, then BlowxFn= BlowyFn+1wherey∈Fn+1C?(n+1), and ifx?C?n,then BlowxFn=BlowyFn?1wherey∈C?(n?1),by Theorem 4.2,we get this corollary. Theorem 4.3Let X be a K3surface and G be a finite Abelian subgroup ofAut(X).If X/G is smooth, then G is isomorphic to one ofAG as groups. ProofSinceX/Gis smooth, the quotient spaceX/Gis an Enriques surface or a rational surface.IfX/Gis Enriques, thenGZ/2Z as a group and Z/2Z ∈AG.By Section 3, ifX/GFn, thenGis isomorphic to one of AGas a group.By [15], ifX/GP2, thenGis isomorphic to one of AGas a group.Therefore,we assume thatX/Gis rational,andX/G≠P2or Fn. Letf:X/G→Fnbe a birational morphism where 0 ≤n≤12,andBbe the branch divisor ofG.By Theorem 4.2 and Corollary 4.1, we may assume that 0 ≤n≤4.By the proof of Proposition 4.1, the numerical class off?Bis one of the list in Section 6. We assume that the numerical class off?Bis one of(6.4), (6.5), (6.6),(6.10),(6.11), (6.12),(6.14), (6.15), (6.16), (6.19), (6.20), (6.25), (6.26), (6.27), (6.28), (6.32), (6.33), (6.36), (6.37),(6.38), (6.41), (6.42), (6.46), (6.51), (6.52), (6.57), (6.58), (6.59), (6.60), (6.79), (6.80), (6.81),(6.82), (6.85), (6.87), (6.88), (6.89), (6.91), (6.94), (6.96), (6.98), (6.112), (6.113), (6.114),(6.115), (6.116), (6.117), (6.118), (6.119), (6.120), (6.121), (6.122), (6.123), (6.124), (6.125),(6.126), (6.176), (6.177), (6.178), (6.180), (6.181), (6.182), (6.183), (6.184), (6.185), (6.186),(6.187), (6.189), (6.190), (6.191), (6.192), (6.195), (6.196), (6.197), (6.199), (6.200), (6.202),(6.203), (6.206), (6.216), (6.217), (6.241), (6.242), (6.243), (6.244), (6.245), (6.246), (6.249),(6.250), (6.270), (6.271), (6.272), (6.273), (6.274), (6.275), (6.276), (6.277), (6.279), (6.282) of the list in Section 6.By Theorem 2.5,Gis generated by automorphismsg1,···,gm, where 1 ≤m≤5 and the order ofgiis two fori=1,···,m.Therefore,Gis Z/2Z⊕awhere 1 ≤a≤5 as a group. We assume that the numerical class off?Bis one of(6.1), (6.2), (6.3),(6.17),(6.18), (6.22),(6.23), (6.24), (6.39), (6.54), (6.55), (6.194), (6.198), (6.201), (6.204), (6.205), (6.212), (6.218),(6.219), (6.228), (6.229), (6.284), (6.285), (6.289), (6.290) of the list in Section 6.By Theorem 2.5,Gis generated by automorphismsg1,···,gm, where 1 ≤m≤3 and the order ofgiis 3 fori=1,···,m.Therefore,Gis Z/3Z⊕bwhere 1 ≤b≤3 as a group. We assume that the numerical class off?Bis one of (6.29), (6.34), (6.40), (6.44), (6.49),(6.50), (6.53), (6.56), (6.62), (6.63), (6.64), (6.66), (6.67), (6.68), (6.69), (6.71), (6.77), (6.83),(6.84),(6.92),(6.93),(6.102),(6.106),(6.107),(6.108),(6.127),(6.128),(6.133),(6.134),(6.135),(6.137), (6.138), (6.145), (6.146), (6.147), (6.148), (6.149), (6.151), (6.153), (6.154), (6.163),(6.164), (6.165), (6.166), (6.167), (6.168), (6.169), (6.174), (6.175), (6.179), (6.188), (6.193),(6.211), (6.214), (6.220), (6.221), (6.223), (6.224), (6.225), (6.226), (6.227), (6.230), (6.236),(6.237), (6.238), (6.239), (6.240), (6.248), (6.251), (6.252), (6.254), (6.256), (6.258), (6.259),(6.260), (6.265), (6.266), (6.267), (6.268), (6.269), (6.283), (6.286), (6.288), (6.292), (6.293),(6.294), (6.295) of the list in Section 6.By Theorem 2.5,Gis generated by automorphismsgi,···,gm,h1,···hn, where 1 ≤m≤3, 1 ≤n≤2, the order ofgiis 2 fori= 1,···,m, and the order ofhjis 3 forj= 1,···,n.Therefore,Gis Z/2Z⊕d⊕Z/3Z⊕e, where (d,e) = (1,1),(1,2), (1,3), (2,1), (2,2), (3,1), (3,2) as a group. We assume that the numerical class off?Bis one of (6.7), (6.8), (6.9), (6.13), (6.21),(6.30), (6.31), (6.35), (6.43), (6.45), (6.47), (6.48), (6.61), (6.86), (6.90), (6.97), (6.99), (6.100),(6.103), (6.104), (6.105), (6.109), (6.110), (6.130), (6.131), (6.139), (6.140), (6.141), (6.142),(6.155), (6.156), (6.157), (6.158), (6.161), (6.162), (6.207), (6.208), (6.209), (6.210), (6.213),(6.215), (6.222), (6.231), (6.232), (6.233), (6.234), (6.255), (6.257), (6.261), (6.262), (6.263),(6.264),(6.278), (6.280), (6.281),(6.287), (6.291)of the list in Section 6.By Theorem 2.5,Gis generated by automorphismsgi,···,gm,h1,···,hn,where the order ofgiis 2 fori=1,···,m,the order ofhjis 4 forj=1,···,n, and (n,m) is one of(0,1), (0,2), (0,3), (1,1),(1,2), (2,1),(3,1).Therefore,Gis Z/2Z⊕f⊕Z/4Z⊕g, where (f,g)=(0,1), (0,2), (0,3), (1,1), (1,2), (2,1),(3,1) as a group. We assume that the numerical class off?Bis (6.65) of the list in Section 6.We denoteBbywheref?Bi1,0= (1,0),f?Bi0,1= (0,1)in Pic(P1× P1), andB′jis an exceptional divisor offforj= 1,···,l.By Theorem 2.5,GZ/2Z⊕i⊕Z/3Z⊕Z/4Z wherei=0 or 1.IfGZ/2Z⊕Z/3Z⊕Z/4Z, thenGis one of AGas a group.We assume thatGZ/3Z ⊕Z/4Z.By Remark 4.2, there are integersβ,aj≥0 such that SinceGZ/3Z ⊕Z/4Z,β=1, 2, 3, 4, 6 or 12.Sincef?B=3(1,0)+6(1,0)+2(1,1)+4(0,1)+4(0,1), the support off?Bis simple normal crossing.Since each irreducible component off?Bis smooth,aj=0 or 1 for each 1 ≤j≤5.Sincef?B=3(1,0)+6(1,0)+2(1,1)+4(0,1)+4(0,1),the non-zero element of{a1,a2}is just one,and the non-zero element of{a4,a5}is just one.The integers which satisfy the above condition are (β,a1,a2,a3) = (12,1,0,1) and (a4,a5) = (1,0)or (0,1).Therefore,f(ei) ?f?B21,0fori= 1,···,l.By the fact thatf?B21,0= (1,0) andf?B1,1= (1,1) in Pic(P1× P1) and the fact thatf(ei) ?f?B21,0fori= 1,···,l, we get thatB21,0∩B1,1is not an empty set, and hencep?1(B21,0)∩p?1(B1,1) is an empty set.SinceGZ/3Z ⊕Z/4Z, the number of subgroup ofGwhich is generated by a non-symplectic automorphism of order 2 is one.Since each ramification index ofB21,0andB1,1is divided by 2,by Theorem 2.5, there is a non-symplectic automorphismgof order 2 such that Fix(g)?f?1B21,0and Fix(g) ?f?1B1,1.Sincep?1(B21,0)∩p?1(B1,1) ≠ ?, this is a contradiction.Therefore, if the numerical class off?Bis (6.65), thenGis one of AGas a group. As for the case of (6.65), if the numerical class off?Bis one of (6.95), (6.136), (6.150),(6.159), (6.235), (6.247), (6.253) of the list in Section 6, thenGis one of AGas a group. We assume that the numerical class off?Bis(6.70)of the list in Section 6.We denoteBbywheref?Bi1,0=(1,0),f?Bi0,1=(0,1),andB′jis an exceptional divisor offforj=1,···,l.By Theorem 2.5,GZ/2Z⊕i⊕Z/3Z⊕Z/4Z wherei=0,1 or 2.There are some integersβ,ajsuch that SinceGZ/2Z⊕i⊕Z/3Z ⊕Z/4Z wherei= 0,1 or 2, we getβ=1, 2, 3, 4, 6 or 12.Sincef?B=2(1,0)+3(1,0)+6(1,0)+2(0,1)+4(0,1)+4(0,1), the support off?Bis simple normal crossing.Since each irreducible component off?Bis smooth,aj= 0 or 1 for each 1 ≤j≤6, and by Proposition 4.2 the non-zero element of {a1,a2,a3} is just one, and the non-zero element of {a4,a5,a6} is just one.From the above, (β,a1,a2,a3,b1,b2,b3) = (1,1,0,0,1,0,0).Therefore,f(ej) ∈f?(B11,0)∩f?(B10,1) forj= 1,···,l.Since ((1,0)·(1,0)) = 0, we get that(p?Bi1,0·p?Bi1,0) =0 fori= 2,3.SinceXis aK3 surface, the support ofp?Bi1,0is a union of elliptic curves fori=2,3.SinceGZ/2Z⊕i⊕Z/3Z⊕Z/4Z wherei=0,1 or 2,the number of subgroups ofGwhich are generated by a non-symplectic automorphism of order 3 is one, and hence there is a non-symplectic automorphismgof order 3 such that Fix(g) has at least two elliptic curves.By [1,14], this is a contradiction.Therefore, the numerical class off?Bis not(6.70). As for the case of (6.70), the numerical class off?Bis not one of (6.75), (6.143) of the list in Section 6. If the numerical class off?Bis (6.72) of the list in Section 6, then by Theorem 2.5,GZ/2Z⊕i⊕Z/4Z⊕jwhere (i,j) is one of (0,1), (0,2), (1,1), (1,2), (2,1), (2,2), (3,1).We assume thatGZ/2Z⊕2⊕Z/4Z⊕2.SinceGis generated by non-symplectic automorphism of order 2 and 4,Gs:= {g∈G:gis symplectic}Z/2Z⊕2⊕Z/4Z.By the classification of finite symplectic groups (see [13, 10, 16]), we see that there is noGswhereGsZ/2Z⊕2⊕Z/4Z.Therefore,GZ/2Z⊕i⊕Z/4Z⊕jwhere (i,j) is one of (0,1), (0,2), (1,1), (1,2), (2,1), (3,1),and if the numerical class off?Bis (6.72), thenGis one of AGas a group. As for the case of (6.72), if the numerical class off?Bone of (6.74), (6.78), (6.111), (6.144)of the list in Section 6, thenGis one of AGas a group. We assume that the numerical class off?Bis (6.73) of the list in Section 6.We denoteBbyBy Theorem 2.5,GZ/2Z⊕i⊕Z/3Z ⊕Z/4Z wherei=0,1 or 2.As for the case of (6.68), there are integersβ,ajsuch that andaj=0 or 1 for each 1 ≤j≤6,β=1,2,3,4,6 or 12, the non-zero element of {a1,a2,a3} is only one, and the non-zero element of {a4,a5,a6} is only one, however, integers which satisfy the above condition do not exist.Therefore, the numerical class off?Bis not (6.73). As for the case of (6.73), the numerical class off?Bis not one of (6.101), (6.129), (6.132),(6.152), (6.160), (6.170), (6.171), (6.172), (6.173) of the list in Section 6. We assume that the numerical class off?Bis (6.76) of the list in Section 6.We denoteBbywheref?B1i,0= (1,0),f?Bi0,1= (0,1) in Pic(P1×P1) andf?B′i= 0.By Theorem 2.5,GZ/2Z⊕i⊕Z/4Z, wherei= 0,1,2,3 or 4.We assume thatGZ/2Z⊕4⊕Z/4Z.By Theorem 2.5,G=G11,0⊕G21,0⊕G10,1⊕G20,1⊕G30,1.As for the case of(6.70),we get thatf(ei)∈B11,0∩Bj0,1for eachi=1,···,mwherej= 1,2,3,4.Therefore, we get (B21,0·Bj0,1) = 1.Lets∈G21,0be a generator.SinceG=G11,0⊕G21,0⊕G10,1⊕G20,1⊕G30,1, by Theorem 2.5, there is a non-symplectic automorphismt∈Gj0,1for somej=1,2,3 such that Fix(t?s) does not have a curve.Since (B12,0·B0j,1)=1 and |G| = 234, we get that |p?1(B21,0)∩p?1(Bj0,1)| = 8.By [2, Proposition 1], the number of isolated points of Fix(t?s) is 4.This is a contradiction.Therefore, if the numerical class off?Bis (6.76), thenGZ/2Z⊕i⊕Z/4Z wherei=0,1,2 or 3, and henceGis one of AGas a group. We assume that the numerical class off?Bis (6.150) of the list in Section 6.We denoteBbywheref?Bis,t=sC+tFin Pic(F1), andB′jis an exceptional divisor offforj=1,···,l.By Theorem 2.5,GZ/2Z⊕i⊕Z/3Z⊕Z/4Z wherei= 0 or 1.Then the number of subgroup ofGwhich is generated by a non-symplectic automorphism of order 3 is one.By the above, forei, there are integersβ,aj≥0 such that SinceGZ/3Z ⊕Z/4Z,β=1, 2, 3, 4, 6 or 12.Sincef?B=3(1,0)+6(1,0)+2(1,1)+4(0,1)+4(0,1), the support off?Bis simple normal crossing.Since each irreducible component off?Bis smooth,aj= 0 or 1 for each 1 ≤j≤5.The integers which satisfy the above condition are (β,a1,a2,a3,a4,a5) = (4,0,0,1,0,1).Therefore,f(ei) ?f?B1,0∩f?B20,1fori= 1,···,land hencep?1(B1,0)∩p?1() is not an empty set.SinceG1,0Z/3Z,Z/12Z, andp?1(B1,0)∩p?1(B20,1) is not an empty set, we get that the number of subgroup ofGwhich is generated by a non-symplectic automorphism of order 3 is at least two.This is a contradiction.Therefore, the numerical class off?Bis not (6.150). As for the case of (6.150), the numerical class off?Bis not (6.159) of the list in Section 6. LetEbe an Enriques surface andHbe a finite Abelian subgroup of Aut(E)such thatE/His smooth.LetXbe theK3-cover ofE, andG:= {s∈Aut(X) :sis a lift of someh∈H}.ThenGis a finite Abelian group,Ghas a non-symplectic involution whose fixed locus is empty,X/G=E/H, and the branch divisor ofGis that ofH. Theorem 5.1Let E be an Enriques surface and H be a finite subgroup ofAut(E).We assume that the quotient space E/H is smooth and there is a birational morphism from E/H to a Hirzebruch surfaceFn, where0 ≤n.Then0 ≤n≤4. ProofLetf:E/H→Fnbe a birational morphism, andbe the branch divisor of the quotient mapE→E/H.Since the canonical line bundle of an Enriques surface is numerically trivial, by Theorem 2.4, the numerical class off?Bis one of Section 3.By[11, Proposition 4.5],Gdoes not have a non-symplectic automorphism whose order is odd.Therefore,biis even number for eachi=1,···,kby Theorem 2.5.By the list of the numerical class of Section 3, we get the claim. Theorem 5.2For each numerical classes(6.6), (6.8), (6.9), (6.11), (6.12), (6.13), (6.16),(6.89), (6.90), (6.91), (6.94), (6.96), (6.97), (6.98), (6.101), (6.203), (6.206), (6.209), (6.210),(6.281)of the list in Section6, there is an Enriques surface E and a finite Abelian subgroup H ofAut(E)such that E/H is a Hirzebruch surfaceFn, and the numerical class of the branch divisor B of the quotient map E→E/H is(6.6), (6.8), (6.9), (6.11), (6.12), (6.13), (6.16),(6.89), (6.90), (6.91), (6.94), (6.96), (6.97), (6.98), (6.101), (6.203), (6.206), (6.209), (6.210),(6.281). Furthermore, for a pair(E,H)of an Enriques surface E and a finite Abelian subgroup H ofAut(E), if E/HFnand the numerical class of the branch divisor B of the quotient map E→E/H is(6.6), (6.8), (6.9), (6.11), (6.12), (6.13), (6.16), (6.89), (6.90), (6.91), (6.94),(6.96), (6.97), (6.98), (6.101), (6.203, (6.206), (6.209), (6.210), (6.281), then H isZ/2Z⊕2,Z/4Z⊕2,Z/2Z ⊕Z/4Z,Z/2Z⊕4,Z/2Z⊕3,Z/2Z⊕2⊕Z/4Z,Z/2Z⊕3,Z/2Z⊕2,Z/2Z ⊕Z/4Z,Z/2Z⊕3,Z/2Z⊕3,Z/2Z⊕3,Z/2Z⊕2⊕Z/4Z,Z/2Z⊕4,Z/4Z⊕Z/8Z,Z/2Z⊕2,Z/2Z⊕3,Z/4Z⊕2,Z/2Z⊕2⊕Z/4Z,Z/4Z ⊕Z/8Z, in order, as a group. ProofLetXbe theK3-cover ofE,G:= {s∈Aut(X) :sis a lift of someh∈H}, andp:X→X/Gbe the quotient map.ThenGis a finite Abelian group,X/GFn, and the branch divisor ofpisB.Sincebiis power of two for eachi=1,···,k,GZ/2Z⊕s⊕Z/4Z⊕t⊕Z/8Z⊕uwheres,t,u≥0.By Theorem 2.5, and the assumption thatGhas a non-symplectic automorphism of order 2 such that whose fixed locus is an empty set, we gets+t+u≥3, and hence the numerical class ofBis one of (6.6), (6.8), (6.9), (6.10), (6.11), (6.12), (6.13), (6.15),(6.16), (6.19), (6.20), (6.81), (6.82), (6.87), (6.88), (6.89), (6.90), (6.91), (6.94), (6.96), (6.97),(6.98), (6.100), (6.101), (6.199), (6.200), (6.203), (6.206), (6.208), (6.209), (6.210), (6.281),(6.282) of the list in Section 6. We assume that the numerical class ofBis (6.6).We denoteBby 2B11,0+2B21,0+2B2,2+2B10,1+2B20,1.By Proposition 3.3,G=G11,0⊕G2,2⊕G10,1Z/2Z⊕3.Lets,t,u,∈Gbe generators ofG11,0,G10,1andG2,2, respectively.Then the non-symplectic automorphisms ofGares,t,u, ands?t?u. From here, we will show that Fix(s?t?u) is an empty set.We assume that the curves of Fix(s) are onlyp?1(B11,0).Sincesis a non-symplectic automorphism of order 2, the quotient spaceX/〈s〉is a smooth rational surface.The quotient mapq:X/〈s〉→X/GP1×P1is the Galois cover such that the branch divisor is 2B20,1+2B2,2+2B10,1+2B20,1, and the Galois group is isomorphic to Z/2Z⊕2as a group.By Theorem 3.1, there is the Galois coverg:Y→X/Gwhose branch divisor is 2B2,2+2B10,1+2B20,1and Galois group is isomorphic to Z/2Z⊕2as a group.Since Fix(s) is not an empty set and the order ofsis 2,X/〈s〉 is a smooth rational surface.By Theorem 2.2, there is the Galois coverh:X/〈s〉 →Ysuch thatq=g?h.Since the degree ofqis 4 and that ofgis 4,his an isomorphism.Since the branch divisor ofqis not that ofg, this is a contradiction.Therefore, Fix(s) isp?1(B11,0)∪p?1(B21,0).In the same way,Fix(t) isp?1(B10,1)∪p?1(B20,1).Therefore, by Theorem 2.5, Fix(s?t?u) is an empty set, and henceE:=X/〈s?t?u〉 is an Enriques surface.LetH:=G/〈s?t?u〉.ThenE/HP1×P1,HZ/2Z⊕2, and the branch divisor ofHisB.It is easy to show that for an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HP1×P1if the numerical class ofHis (6.6), thenHZ/2Z⊕2. As for the case of (6.6), the claim is established for (6.89). We assume that the numerical class ofBis (6.8).We denoteBby 4B11,0+4B21,0+2B1,1+4B10,1+4B20,1.By Proposition 3.3,G=G11,0⊕G1,1⊕G10,1Z/2Z ⊕Z/4Z⊕2.Lets,t,u∈Gbe generators ofG11,0,G10,1andG1,1, respectively.By Theorem 2.5,sandtare non-symplectic automorphism of order 4 anduis a non-symplectic automorphism of order 2.By Theorem 2.5,G21,0is generated bys?t2x?uywherex,y= 0 or 2.Since (s?t2x?uy)2=s2forx,y= 0 or 2, we get that Fix(s2) isp?1(B11,0)∪p?1(B21,0).As for the case of (6.6), we get the claim for(6.8). As for the case of (6.8), the claim is established for (6.101). We assume that the numerical class ofBis (6.9).We denoteBby 4B11,0+4B21,0+2B1,2+2B10,1+2B20,1.By Proposition 3.3,G=G11,0⊕G1,2⊕G10,1Z/2Z⊕2⊕Z/4Z.Lets,t,u∈Gbe generators ofG11,0,G10,1andG1,2, respectively.As for the case of(6.6), Fix(t)isp?1(B10,1)∪p?1(B20,1).As for the case of (6.8), Fix(s) is the support ofp?1(B11,0)∪p?1(B21,0).As for the case of (6.6), we get the claim for (6.101). We assume that the numerical class ofBis (6.10).We denoteBby 2B11,0+2B21,0+2B31,0+2B1,4.Lets1,s2,t∈Gbe generators ofG11,0,G21,0andG1,4, respectively.By Proposition 3.3,G=G11,0⊕G21,0⊕G1,4Z/2Z⊕3.Then the non-symplectic involutions ofGares1,s2,tands1?s2?t. We assume that Fix(s1)isp?1(B11,0)∪p?1(B31,0).ThenX/〈s1〉is a smooth rational surface,and the quotient mapq:X/〈s1〉 →X/GP1×P1is the Galois cover such that the branch divisor is 2B20,1+ 2B1,4, and the Galois group is isomorphic to Z/2Z⊕2as a group.Since P1× P1B21,0is simply connected, in the same way of the proof of Theorem 2.5, this is a contradiction.Therefore,Fix(si)isp?1(Bi1,0)fori=1,2,and hence Fix(s1?s2?t)isp?1(B31,0).There is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HP1×P1and the numerical class of the branch divisor ofHis (6.10). As for the case of (6.10), we get the claim for (6.87), (6.100). We assume that the numerical class ofBis (6.11).We denoteBby 2B11,0+2B21,0+2B31,0+2B1,1+2B10,1+2B20,1+2B30,1.By Proposition 3.3,G=⊕2i=1Gi1,0⊕G1,1⊕2i=1Gi0,1, and hence the number of non-symplectic automorphisms of order 2 ofGis 16.By Theorem 2.5,Ghas a non-symplectic automorphism of order 2 whose fixed locus is an empty set.Furthermore, it is easy to show that for an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HP1×P1if the numerical class ofHis (6.11), thenHZ/2Z⊕4. As for the case of (6.11), the claim is established for (6.12), (6.13), (6.16), (6.91), (6.94),(6.96), (6.97), (6.98), (6.206), 6.210). We assume that the numerical class ofBis (6.15).We denoteBby 2B11,0+2B21,0+2B11,2+2B21,2.By Proposition 3.4,G=G11,0⊕G11,2⊕G21,2.Lets,t,u∈Gbe generators ofG11,0,G11,2andG21,2, respectively.Then the non-symplectic automorphisms of order 2 ofGares,t,uands?t?u.We assume that Fix(s?t?u) is an empty set.Since (Bi1,0·Bj1,2) ≠ 0 fori,j= 1,2,Fix(s)isp?1(B11,0)∪p?1(B21,0).Since(B11,0+B21,0·B11,2)=4,X/(G11,0⊕G11,2)is smooth.SinceG=G11,0⊕G11,2⊕G21,2, the branch divisor of the quotient mapX/(G11,0⊕G11,2)→X/GF2is 2B21,0and its degree is 2.SinceandX/(G11,0⊕G11,2) is smooth, this is a contradiction.Therefore, there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HF1and the numerical class of branch divisor ofHis (6.15). As for the case of(6.15),we get that there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HFnand the numerical class of the branch divisor ofHis (6.88). We assume that the numerical class ofBis (6.19).We denoteBby 2B11,1+2B21,1+2B31,1+2B41,1.By Proposition 3.6,G=G11,1⊕G21,1⊕G31,1.Letsi∈Gi1,1be a generator ofGi1,1fori=1,2,3,4.By Theorem 2.5, Fix(si) is not an empty set fori=1,2,3,4.SinceGZ/2Z⊕3,s4=s1?s2?s3, and henceGdoes not have a non-symplectic automorphism of order 2 whose fixed locus is an empty set.Therefore, there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HF1and the numerical class of the branch divisor ofHis (6.19). As for the case of(6.19),we get that there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HFnand the numerical class of the branch divisor ofHis (6.19), (6.20), (6.81), (6.82), (6.200). We assume that the numerical class ofBis (6.90).We denoteBby 2B1,0+2B1,1+2B2,2+4B10,1+ 4B20,1.By Corollary 3.3,G=G1,1⊕G2,2⊕G10,1.Letq:X/〈G1,0,G1,1,G2,2〉 →X/GF1be the quotient map.Then the branch divisor ofqis 4B10,1+4B20,1.By Theorem 2.2,X/〈G1,0,G1,1,G2,2〉F4, and the branch divisor of 〈G1,0,G1,1,G2,2〉 is 2B1,0+2q?B1,1+2q?B2,2.Lets,t,u∈Gbe generators ofG1,1,G2,2andG10,1, respectively.Then Fix(s) is the support ofp?B1,0and that ofp?B1,1.Then as for the case of (6.6), we get the claim. As for the case of (6.90), the claim is established for (6.203), (6.209), (6.281). We assume that the numerical class ofBis(6.199).We denoteBby 2B1,0+2B1,4+2B11,2+2B21,2.By Corollary 3.5,G=G1,4⊕G11,2⊕G21,2.Lets,t,u∈Gbe generators ofG1,4,G11,2andG21,2, respectively.Then the non-symplectic automorphisms ofGares,t,uands?t?u.Since each fixed locus ofs,tanduis not an empty set, by Theorem 2.5, ifGhas a non-symplectic automorphism of order 2 whose fixed locus is an empty set,then that iss?t?u.We assume that Fix(s?t?u) is an empty set.Then we may assume that Fix(t) isp?1(B1,0)∪p?1(B11,2).Since(B1,0+B11,2·B1,4)=6, we get |p?1(B1,0∪B11,2)∩p?1(B1,4)| =12.Sinces?tis a symplectic automorphism of order 2 andp?1(B1,0∪B11,2)∩p?1(B1,4) is contained in Fix(s?t), this is a contradiction.Therefore, there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HF1and the numerical class of the branch divisor ofHis (6.199). We assume that the numerical class ofBis(6.208).We denoteBby 4B1,0+2B1,3+4B1,2+2B10,1+2B20,1.By Proposition 3.8,G=G1,3⊕G1,2⊕G10,1.Lets,t,u∈Gbe generators ofG1,3,t∈G1,2andu∈G10,1, respectively.Then the non-symplectic automorphisms ofGares,t2,uands?t2?u.Since each fixed locus ofs,t2anduis not an empty set by Theorem 2.5, ifGhas a non-symplectic automorphism of order 2 whose fixed locus is an empty set, then that iss?t2?u. We assume that Fix(s?t2?u) is an empty set.Then Fix(t2) isp?1(B1,0)∪p?1(B1,2) and Fix(u) isp?1(B11,0)∪p?1(B21,0).Since (B1,3·B10,1+B20,1) = 4, we get thatX/(G1,3⊕G10,1)is smooth, and the branch divisor of the quotient mapf:X/(G1,3⊕G10,1) →X/GF2is 4B1,0+4B1,2, and the Galois group is Z/4Z, which is induced byt.Furthermore, since(B1,3·B1,0+B1,2) = 4 and (B1,3·B10,1+B20,1) = 4,G/〈s,t2,u〉 is smooth, and the branch divisor of the quotient mapg:X/〈s,t2,u〉 →X/GF2is 2B1,0+2B1,2, and the Galois group is isomorphic to Z/2Z as a group.LetE1,0andE1,2be the support ofg?B1,0andg?B1,2, respectively.Theng?B1,0= 2E1,0andg?B1,2= 2E1,2.Moreover, by Theorem 3.1,there is the double coverh:X/(G1,3⊕G10,1) →X/〈s,t2,u〉 such thatf=g?hand the branch divisor is 2E1,0+2E1,2.SinceX/(G1,3⊕G10,1) andX/〈s,t2,u〉 are smooth, we getSinceg?B1,2=g?B1,0+2g?Fin Pic(X/〈s,t2,u〉), SinceX/〈s,t2,u〉 is a smooth rational surface, Pic(X/(G1,3⊕G10,1)) is torsion free.Therefore,we get and hence Since(B1,0·F)=1,the degree ofgis two,are elements of Pic(X/〈s,t2,u〉), this is a contradiction.Therefore, there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E)such thatE/HF1and the numerical class of the branch divisor ofHis(6.208). We assume that the numerical class ofBis(6.282).We denoteBby 2B1,0+2B11,4+2B21,4+2B31,4.By Corollary 3.5,G= ⊕3i=1Gi1,4.Letsi∈Gi1,4be a generator fori= 1,2,3.Then the non-symplectic automorphisms ofGaresiands1?s2?s3wherei= 1,2,3.Since each fixed locus ofsiis not an empty set for eachi= 1,2,3 by Theorem 2.5, ifGhas a non-symplectic automorphism of order 2 whose fixed locus is an empty set, then that iss1?s2?s3.We assume that Fix(s1?s2?s3)is an empty set.Then we may assume that Fix(s1)isp?1(B1,0)∪p?1(B11,4).Since (B1,0+B11,4·B1,4)=4, we get thatX/(G11,4⊕G21,4) is smooth, and the branch divisor of the quotient mapX/(G11,4⊕G11,4)→X/GF4is 2B31,4.This is a contradiction as the degree of the quotient map is 2.Therefore, there is not an Enriques surfaceEand a finite Abelian subgroupHof Aut(E) such thatE/HF4and the numerical class of the branch divisor ofHis (6.282). By Theorem 5.2, we get Theorem 1.7. Theorem 5.3Let E be an Enriques surface and H be a finite Abelian subgroup ofAut(E).If E/H is smooth, then H is isomorphic to one ofAG(E)as a group. ProofLetXbe theK3-cover ofE,G:= {s∈Aut(X) :sis a lift of someh∈H},andp:X→X/Gbe the quotient map.ThenGis a finite Abelian group,X/G=E/H,and the branch divisor ofpisB.We classifiedHfor the case ofE/HFnin Theorem 5.2.From here, we assume thatE/His smooth andE/H/Fnor P2.SinceGdoes not have a non-symplectic automorphism whose order is odd (see [11]), by Theorems 2.5 and 1.4,GZ/2Z⊕s⊕Z/4Z⊕t⊕Z/8Z⊕uwheres,t,u≥0.By the assumption thatGhas a nonsymplectic automorphism of order 2 such that whose fixed locus is an empty set, and the fact thatGis generated by non-symplectic automorphisms whose fixed locus have a curve, we gets+t+u≥3.Therefore,Gis one of the following as a group: IfGis one of as a group, then quotient groupG/KofGby a subgroupKZ/2Z is one of as a group.Letf:X/G→Fnbe the birational morphism.We assume thatGZ/4Z⊕3.By the assumption thatGZ/4Z⊕3and Theorem 2.5, the numerical class off?Bis only(6.142).We denoteBbywheref?B1,0=C,f?Bi1,4=C+4F,f?Bi0,1=Fandf?B′i=0 in Pic(F4).SinceGZ/4Z⊕3, by Theorem 2.5,we get thatG=G11,4⊕G21,4⊕G10,1.Lets∈G11,4,t∈G21,4andu∈be generators respectively.The non-symplectic involutions ofGares2,t2,u2ands2?t2?u2.Since each fixed locus ofs2,t2andu2is not an empty set, ifGhas a non-symplectic automorphism of order 2 whose fixed locus is an empty set, then that iss2?t2?u2.If the fixed locus ofs2?t2?u2is an empty set,then the fixed locus ofs?t?uis an empty set.By [2], this is a contradiction.Therefore,Gis not Z/4Z⊕3as a group. We assume thatGZ/2Z ⊕Z/4Z ⊕Z/8Z.By Theorem 2.5, the numerical class off?Bis only (6.101).By the proof of Theorem 4.3,fis an isomorphism, i.e.,X/GF1.By Theorem 5.2, we get the claim. By Theorems 5.2–5.3, we get Theorem 1.8. Here, we will give the list of a numerical class of an effective divisoron Fnsuch thatBiis a smooth curve for eachi=1,···,kand If there is aK3 surfaceXand a finite subgroupGof Aut(X)such thatX/G=F0P1×P1,then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF1, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF2, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF3, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF4, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF5, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF6, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF7, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF8, then by Theorem 2.4 the numerical class ofBis one of the following: If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF9, then by Theorem 2.4 the numerical class ofBis one of the following: By Theorem 2.4 there is not aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GFlforl=10,11. If there is aK3 surfaceXand a finite subgroupGof Aut(X) such thatX/GF12, then by Theorem 2.4 the numerical class ofBis the following:3 Abelian Groups of K3 Surfaces with Hirzebruch Surfaces
3.1 Abelian covers of a Hirzebruch surface by a K3 surface
3.2 Complete proof of Theorem 1.5
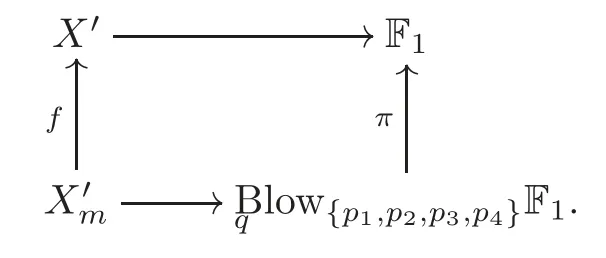
4 Abelian Groups of K3 Surfaces with Smooth Quotient
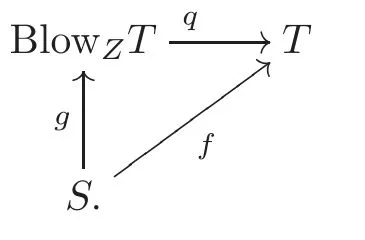
5 Abelian Groups of Enriques Surfaces with Smooth Quotient
6 The List of a Numerical Class
 Chinese Annals of Mathematics,Series B2023年1期
Chinese Annals of Mathematics,Series B2023年1期
