Kun Wang(王堃) Chuan Dong(董川) Yi-Zhi Qu(屈一至) Ling Liu(劉玲) Yong Wu(吳勇)Xu-Hai Hong(洪許海) and Robert J.Buenker

1Institute of Environmental Science,Shanxi University,Taiyuan 030006,China

2College of Optoelectronics,University of Chinese Academy of Sciences,Beijing 100049,China

3National Key Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

4School of Physics and Electronic Technology,Liaoning Normal University,Dalian 116029,China

5Fachbereich C-Mathematik und Naturwissenschaften,Bergische Universitat Wuppertal,D-42097 Wuppertal,Germany

Keywords: electron excitation processes,low energy collision,quantum-mechanical molecular orbital closecoupling method,cross section

1. Introduction

In modern astrophysics, the determination of the chemical compositions of stars by high-resolution spectroscopy is one of the fundamental issues.[1,2]For the past few years, in order to have a deeper understanding of stellar physics and uncover the mysteries of the formation history of the galaxy,millions of star spectral data have been collected through ground devices and satellite surveys,[3]for example,RAVE,[4]GAYAESO[5]and Gaia satellite.[6]Moreover,when determining the absolute and relative abundance of the elements in the stellar atmosphere, which plays an important role in astronomical observation,[7]the non-local thermodynamic equilibrium(non-LTE)effect should be considered.

The most important mechanism in the non-LTE modeling of stellar spectra is the atom–atom inelastic collision process.[8]This process determines the properties of gas and plasmonic media in many cases, especially when hydrogen and helium, the most abundant elements in the universe, are involved,[9]e.g., with Hubble Space Telescope (HST) Cosmic Origins Spectrograph(COS),it is observed that the spectra of helium-dominated white dwarfs and atmospheric hydrogen exhibit a distinctive broad feature.[10]Although H + He is one of the simplest atom–atom inelastic collision systems with only three electrons, it is complex enough to give rise to the main types of inelastic reactions, and the interactions are quite difficult to compute with the accuracy that is needed.Therefore,this collision process has attracted great interest for decades.[11–25]

In the low-energy region,the main reaction of the H+He collision is the excitation process

From the viewpoint of theory, challenges still remain in this process: owing to the strong couplings between different states and the electron correlation effects,the neglect of the influence of higher excited states(H(n ≥3))for the system may not be acceptable.[22]Moreover, there exist relatively large discrepancies between measured and calculated results.[11–23]

In the present work, the excitation processes H(1s)+He(1s2)→H(2s/2p)+He(1s2)are investigated in the energy region of 20–2000 eV/u by using the quantum-mechanical molecular orbital close-coupling(QMOCC)method. Our calculated cross sections are in better agreement with the experimental data than the previous theoretical works,and the possible reasons are discussed. The relevant electronic structure parameters which are needed in the dynamical calculations,including adiabatic potentials, radial and rotational couplingmatrix elements, have been obtained by using theab initiomultireference single-and double-excitation configurationinteraction(MRD-CI)method.[26,27]

The present paper is organized as follows. In Section 2,the theoretical methods are briefly outlined. Section 3 is divided into two parts: in the first part,we present the molecular potential and coupling data, while the second part is devoted to the analysis of the scattering calculation results and the discussion on the disagreement with previous experimental and theoretical works. While a brief summary is performed in Section 4. Atomic units are used throughout, unless explicitly indicated otherwise.

2. Theory

The excitation processes of H(1s)+He(1s2) collisions are described by the QMOCC method,which has been formulated in detail by Zygelmanet al.[28]and Kimuraet al.,[29]here we just outline a brief introduction.By using the log-derivative method of Johnson,[30]a coupled set of second-order differential equations are solved. Firstly, the total wave functions are expanded by adiabatic electric wave functions,and transitions between channels are driven by elements(radialARand rotationalAθ) of the vector potentialA(R), whereRis the internuclear distance vector. For numerical calculation convenience,a unitary transformation is made to a diabatic representation. By matching the plane-wave boundary conditions at a large nuclear distance,theKmatrix is obtained from the scattering amplitude after a partial-wave decomposition,[28]then the scattering matrixSis written as

whereIrepresents the identity matrix. In this case, the cross section from the initial channelito the final channeljis given by

wherekiis the initial momentum, andJrepresents the total angular momentum.

In the present work, by introducing appropriate reaction coordinates, allowance for the translation effects has been made.[31,32]The radial and rotational coupling matrix elements between the statesψKandψLare transformed into[33]

respectively, whereεKandεLrepresent the energies of statesψKandψL,z2andzxare the components of the quadrupole moment tensor. This modification is similar in form to that obtained by applying the electron translation factor (ETF)method,[34]since the ETF effects are often used to remove asymptotic couplings between atomic states and are expected to be significant for collision energyE>1 keV/u.[35]

3. Results and discussion

3.1. Adiabatic potentials and couplings

The adiabatic potentials and coupling matrix elements for the HeH quasi-molecular system have been obtained by using theab-initioMRD-CI method.[26,27]A threshold of 5.0×10?8Hartree(1.36×10?6eV)is used to select the configurations of the HeH quasi-molecule for internuclear distances from 1.0 a.u. to 3.00 a.u. The potential energy curves of the lowest eight2Σ+states inA1(C2v) symmetry and four2Π states in B1symmetry have been carried out. The higher excited states,such as the H(4d/4f)+He(1s2)states,have relatively little effect on the main excitation process to H(2s/2p),so they are not included in this work. And the2?states have been disregarded since the initial state is a doublet spin2Σ+state and such effects are quite small. The correlationconsistent polarized valence quadruple-zeta(cc-pVQZ)Gaussian basis sets,[36,37]i.e., (6s,3p,2d,1f) and (7s,3p,2d) contracted to[4s,3p,2d,1f]and[4s,3p,2d]have been employed for hydrogen[36]and helium,[37]respectively. In order to describe the Rydberg states of hydrogen atom better,the(4s,3p,2d)diffuse functions of H are added. As shown in Table 1,the energies of HeH quasi-molecule in the asymptotic region are displayed and are compared with the National Institute of Standards and Technology(NIST)data,[38]the errors are less than 0.015 eV,which should be quite adequate for most of the scattering calculations.[39]

As shown in Fig.1,the adiabatic potentials referred to Table 1 have been obtained as a function of internuclear distanceR= 0.10–10.00 a.u. The 12Σ+represents the initial state H(1s2S)+He(1s2). Notably,for each of the excited states of the molecule HeH, there exists a valley nearR ～1.4 a.u.,and the interactions of the initial state with these valleys are likely to lead to a transition from the initial state to the final state. However, in the range of internuclear distanceR<1.00 a.u., the potential energy curves for the initial state and the other excited states are getting closer asRdecreases,so that the avoided crossings with their radial and rotational couplings become more critical. Compared with Ref. [22],other than the most important four states they considered,i.e.,1–32Σ+and 12Π,we also have considered the 3l,4s and 4p Rydberg states of H and have evaluated the influence of these states on the system in the following dynamic calculations.

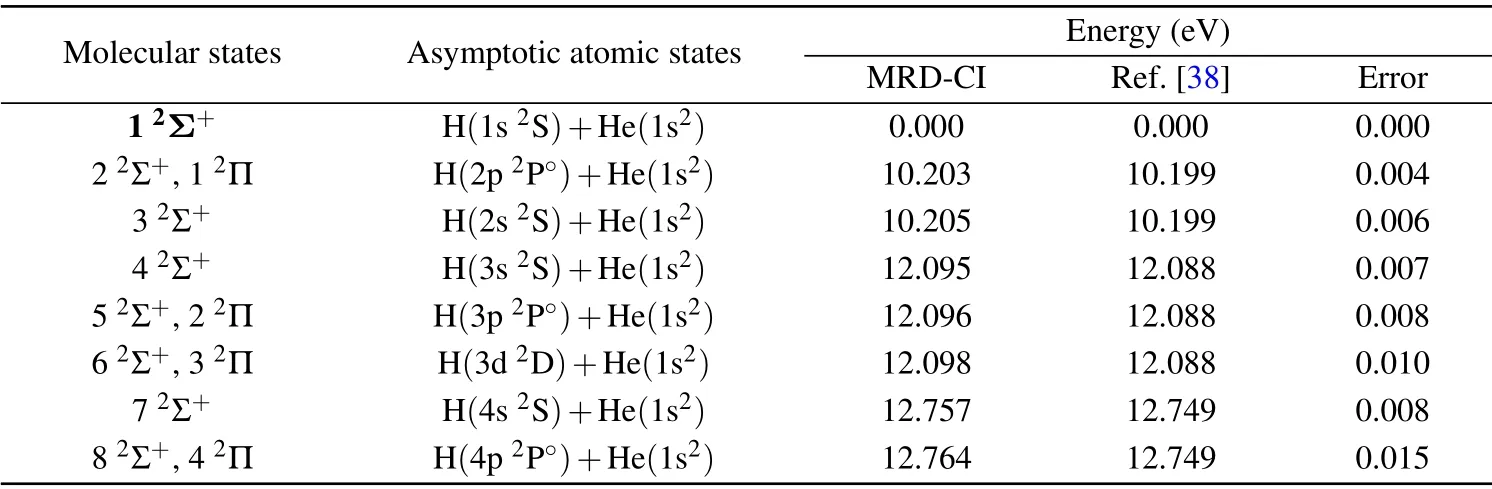
Table 1. Asymptotic separated-atom energies for the states of HeH system. The bold 1 2Σ+ represents the initial state.

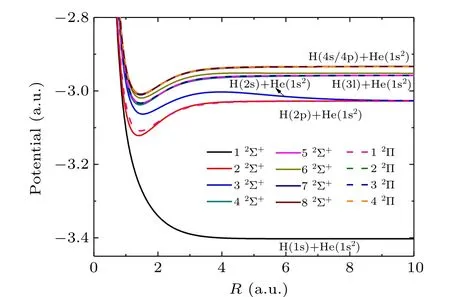
Fig.1. Potential energy curves of HeH molecule refer to Table 1. The solid and dashed lines represent the Σ+ and Π states,respectively.

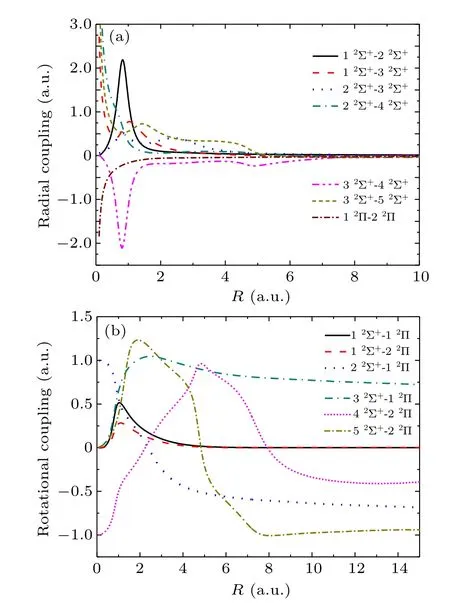
Fig. 2. Coupling matrix elements for HeH molecule: (a) radial coupling matrix elements(b)rotational coupling matrix elements.

The radial and rotational coupling matrix elements between all pairs of states have been calculated with the ETF effects,[33]here some important couplings are displayed in Figs. 2(a) and 2(b). In Fig. 2(a), the initial 12Σ+state(H(1s)+He) is strongly coupled with the exit 22Σ+state(H(2p)+He)at internuclear distancesR ～0.8 a.u., this coupling should be the primary gateway of electron excitation flux toward the exit channels. We can also observe that there are two relatively broader and weaker peaks between 22Σ+and 32Σ+(H(2s)+He)states around 0.9 a.u. and 2.5 a.u.,which implies that with the increase of energy, the scattering cross section may also have a double-peak structure in the considered energy region. Compared with Ref. [22], not only the four most important states(1–32Σ+and 12Π)are included in the present work,but also more Rydberg states with their couplings should be considered,e.g.,the strong coupling between 32Σ+and 42Σ+states aroundR ～0.9 a.u.,which may affect the results of the excitation process.

Some important adiabatic rotational coupling matrix elements are presented in Fig.2(b),these couplings drive the transitions between states of the same spin but of different spatial symmetry. ForR>3.0 a.u.,the 22Σ+and 32Σ+states are rotationally strongly coupled with the 12Π state corresponding to the electron excitation to H(2p)+He exit state.

3.2. Excitation cross sections

The QMOCC method has been employed to investigate the inelastic collision process of H(1s)+He(1s2)→H(2s/2p)+He(1s2), and the excitation cross sections have been obtained for a wide energy range of 20–2000 eV/u.All the datasets presented in this paper, including the excitation cross sections, are compiled in the supplementary materials (SM) in PDF format. First, we have checked the convergence of our calculation results. Considering the potentials with radial and rotational coupling matrix elements of four (1–32Σ+, 12Π, i.e., H(1s/2l)), nine (1–62Σ+, 1–32Π, i.e., H(1s/2l/3l)) and twelve (1–82Σ+, 1–42Π, i.e.,H(1s/2l/3l/4s/4p)) states, the total cross sections of the excitation process to H(2s/2p) have been calculated with the QMOCC method. Good agreement has been found between the excitation cross sections calculated with nine and twelve states(they are almost identical, so the cross sections of nine states are not shown here),which indicates that our results with twelve states are convergent.

As shown in Fig. 3, the excitation cross sections to H(2s/2p) states are compared with the available experimental[12,17,18]and other theoretical[13,14,17,21–23]results. AtE ～20 eV/u, the total excitation cross section is about 0.12×10?16cm2,with the energy increasing,this value shows an upward trend and reaches a maximum of about 0.85×10?16cm2atE ～600 eV/u. However, when the energy exceeds 600 eV/u, the cross section shows a very slow downward trend to 0.79×10?16cm2around 2 keV/u. Compared with all available experimental[12,17,18]data,our results are consistent with them in both trend and magnitude, especially in the overlapping energy range of 100–500 eV/u. It is a pity that the latest experimental results of Van Zylet al.[19]only provided the excitation cross sections to the H(2p)state,as shown in Fig. 4. If we use these data to estimate the total cross section, the difference between our calculation and the experiment results would be less than 15%over a wide energy range from 40 eV/u to 1 keV/u.

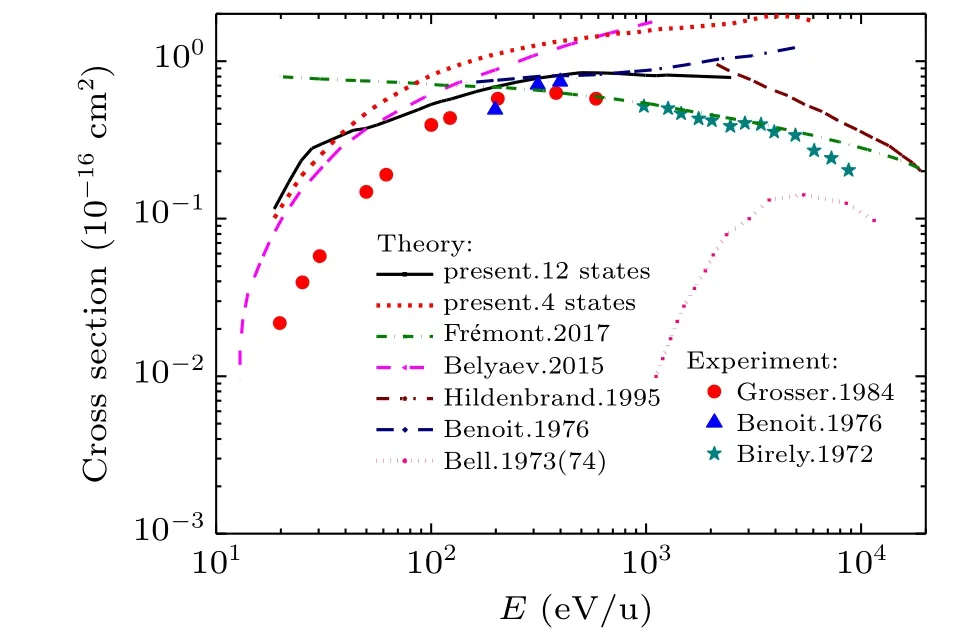
Fig. 3. Comparison between the present total excitation cross sections to H(2l) state with experimental and other theoretical results. The theoretical results include the present calculation considering 12 states(solid line),4 states(short dashed line),the classical trajectory Monte Carlo(CTMC)results of Fr′emont et al.[23](short dash dotted line),quantum chemical results of Belyaev[22] (dashed line),semiclassical approximation results of Hildenbrand et al.[21] (dash dot dotted line), two-state quasi-molecular model results of Benoit et al.[17] (dash dotted line), and Born approximation results of Bell et al.[13,14] (short dotted line). The experimental results are from Grosser et al.[18] (solid circles),Benoit et al.[17] (solid triangles),and Birely et al.[12] (solid pentagram).

Next, compared to all other theoretical[13,14,17,21–23]results, our results show the best overall agreement with the available experimental data. Fr′emontet al.[23]used the classical trajectory Monte Carlo (CTMC) method, while Born approximation method was applied by Bellet al.,[13,14]these two methods are usually suitable for the treatment of highenergy collision with incident energies over tens of keV/u.Benoitet al.[17]estimated the total cross section using the twostate quasi-molecular model method,the lack of consideration of essential channels may have an impact on the final result.Belyaev[22]has used the quantum chemical method, but as mentioned in his paper,only four most important channels(1–32Σ+, 12Π, i.e., H(1s/2l))are included, which influence the accuracy of the numerical results. This can be explained by our work:as shown in Fig.1,in the range ofR<1.00 a.u.,the potential energy curves of the four important states are very close to other highly excited states, while in Fig. 2, it can be found that these four states also have strong couplings with the highly excited states. Therefore, with the increasing incident energy, the impact of the highly excited states on the scattering cross section to H(2s/2p) states would be greater and greater. To verify this, we have also present our results with the four most important states, which agree well with the results of Belyaev,[22]as shown in Fig. 3. In the range ofE<40 eV/u, the results of four states, twelve states and Belyaev are in good agreement. However, as the energy increases, the difference between the results of the twelve and the four states becomes larger and larger. At about 1 keV/u,the cross section of the four states is about 90% larger than that of the twelve states. Finally, we compare the excitation cross sections with the works of Hildenbrandet al.[21]at the energy junction (around 2 keV/u), it can be seen from Fig. 3 that these two calculations are well connected.

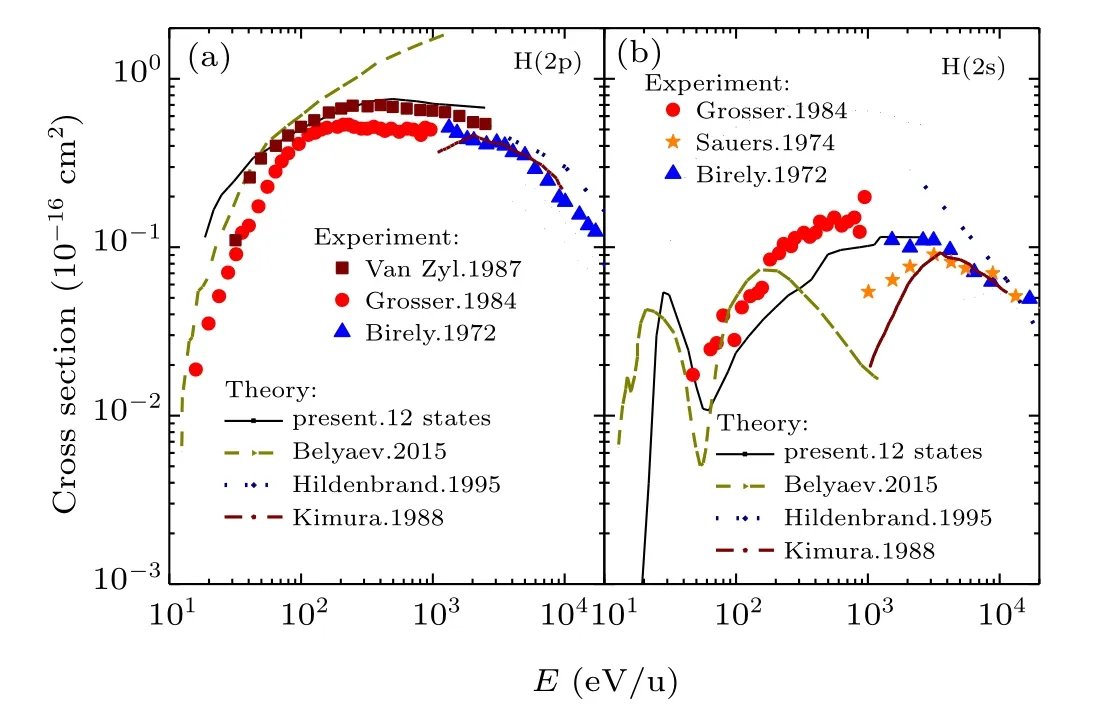
Fig. 4. Comparison between the present excitation cross sections to H(2p) state (a) and H(2s) state (b) with the experimental and other theoretical results. The theoretical results include the present calculation considering 12 states (solid line), quantum chemical results of Belyaev[22](dashed line), semiclassical approximation results of Hildenbrand et al.[21](dotted line), and molecular orbital results of Kimura et al.[20] (dash dotted line). The experimental results are from Grosser et al.[18] (solid circles), Birely et al.[12] (solid triangle), Van Zyl et al.[19] (solid square) and Sauers et al.[15] (solid pentagram).

To validate our results further, the states-selected cross sections to H(2p)and H(2s)are presented and compared with other available theoretical[20–22]and experimental[12,15,18,19]data for the excitation process in Figs. 4(a) and 4(b), respectively. It can be seen that in the energy range considered, the dominant channel for the collision excitation process is the H(2p) states. As can be found in Fig. 4(a), our state-selective cross section of H(2p) agrees well with all experimental[12,18,19]data in terms of numerical values and trends. Especially compared with the latest experimental results of Van Zylet al.,[19]the difference is less than 15%in a fairly wide energy range from 40 eV/u to 1 keV/u.Moreover,other theoretical[20–22]results have been compared.Kimuraet al.[20]adopted pseudopotential to replace the effect of two electrons of the He atom, so their results are different from our in the overlapping energy region. We focus on comparing our results with Belyaev[22]as a similar energy range is considered. For the energyE>40 eV/u,with the increase of energy, the difference between his results and ours becomes more and more extensive. When the energy reaches toE ～1 keV/u, his result is about twice as large as ours. As mentioned above,this is because he has not considered the influences of highly excited states of H(n>2),which may affect their accuracy.

Figure 4(b) shows the excitation state-selective cross section to H(2s) state, compared with the available experimental[12,15,18]results,our calculations agree well with most of the experimental[12,18]results in the overlapping energy region. It is notable that the excitation cross section to H(2s) state shows a peak structure at around 30 eV/u impact energy, and a valley structure when the collision energyE ～60 eV/u, which is consistent with the calculation results of Belyaev,[22]and more accurate experimental data are expect for such structures. In the energy range ofE>60 eV/u, our results show an upward trend with the increasing energy. The reason for the formation of these structures is because there exist two relatively broader and weaker peaks between 22Σ+and 32Σ+(H(2s)+He)states aroundR ～0.9 a.u.and 2.5 a.u.,respectively. However, different from our calculation results,the work of Belyaev[22]shows a second peak structure which is formed nearE ～100 eV/u. There are two reasons for the difference. 1) More excited states have been considered in our work, which would be expected to have effect on the results of excitation cross sections to H(2l) at higher energies.2) The ETF effects have been contained in our calculations,as they would make contributions in the energy range above 1 keV/u.[40]

4. Conclusion

In the present work, a good evaluation about the electron excitation processes of H(1s)+He(1s2)→H(2s/2p)+He(1s2)collision has been provided by the QMOCC method.Total and state-selective cross sections have been calculated and compared with the available theoretical and experimental works in the energy range of 20–2000 eV/u,with theab initiopotential energy curves and nonadiabatic radial and rotational coupling matrix elements obtained by the MRD-CI method.Overall,our present results agree well with available measurements for both total and state-selective cross sections in the respective overlapping energy regions. The dominant channel for the collision excitation process is the H(2p)states,the difference is less than 15% in a fairly wide energy range from 40 eV/u to 1 keV/u when compared with the latest experimental results of Van Zylet al.[19]

The comparison of our results with other theoretical calculations further demonstrates the importance of considering a sufficient number of channels. It is proved that with the increase of the collision energy, the role of the highly excited state becomes more and more significant. The excitation cross section to H(2s)state shows a peak structure at around 30 eV/u impact energy, and a valley structure at about 60 eV/u, when the collision energyE> 60 eV/u, our results show an upward trend with the increasing energy. The formation of these structures is mainly due to the two broad couplings between 22Σ+and 32Σ+(H(2s)+He)states aroundR ～0.9 a.u. and 2.5 a.u., respectively. Our work brings a deeper understanding of atom–atom inelastic collision excitation processes and provides new data beneficial for astrophysical modeling.

Data availability statement

The data that support the findings of this study are openly available in Science Data Bank at https://www.doi.org/10.57760/sciencedb.j00113.00083.

Acknowledgment

This work has been supported by the National Natural Science Foundation of China (Grant Nos. 12204288,11934004,and 12274040).