ITERATIVE METHODS FOR OBTAINING AN INFINITE FAMILY OF STRICT PSEUDO-CONTRACTIONS IN BANACH SPACES*
Meng WEN (文萌) Haiyang LI (李海洋)
1.School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China
2.School of Science,Xi’an Polytechnic University,Xi’an 710048,China
E-mail: wen5495688@163.com;fplihaiyang@126.com
Changsong HU (胡長(zhǎng)松)
Department of Mathematics,Hubei Normal University,Huangshi 435002,China
E-mail: huchang1004@aliyun.com
Jigen PENG (彭濟(jì)根)?
School of Mathematics and Information Science,Guangzhou University,Guangzhou 510006,China
E-mail: jgpengxjtu@126.com
Abstract In this paper,we introduce a general hybrid iterative method to find an infinite family of strict pseudo-contractions in a q-uniformly smooth and strictly convex Banach space.Moreover,we show that the sequence defined by the iterative method converges strongly to a common element of the set of fixed points,which is the unique solution of the variational inequality,for z ∈Γ(Si).The results introduced in our work extend to some corresponding theorems.
Key words MKC;iterative algorithm;strict pseudo-contraction;β-Lipschitzian;δ-strongly monotone;Banach spaces
1 Introduction
Assume thatEis a real Banach space.LettingJ:E→2E*,we define the normalized duality mapping by
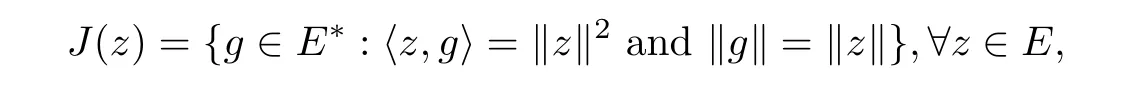
where 〈·,·〉 is the generalized duality pairing,andE*is the dual space ofE.In addition,we will usejto denote the single-valued normalized duality mapping.Let {zk} be a sequence inE.
Thus we usezk→(respectively,) to denote strong (respectively,weak,weak*)convergence of the sequence {zk} to ˉz.Assume thatJis single valued if,for each {zk} ?Ewith,one has;thusJis said to be weakly sequentially continuous.
Lettingq >1,we useJqto denote the generalized duality mapping,which is given by
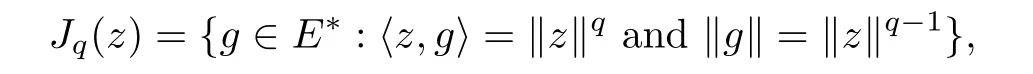
and the following relation holds:
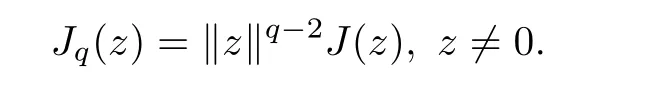
LettingμE: [0,∞) →[0,∞),the modulus of the smoothness ofEis given by
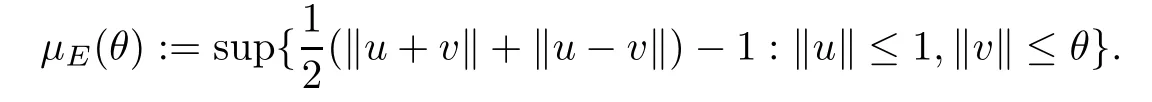
Givenq >1,if there is a constantb >0 such thatμE(θ) ≤bθq,thenEisq-uniformly smooth.The example of such spaces areLp(orlp),p >1 and Hilbert spaces.More specifically,for eachp >1,Lp(orlp) is min{p,2} -uniformly smooth.
Noticing that aq-uniformly smooth Banach space is uniformly smooth,this means that its norm is uniformly Fréchet differentiable [1].
WhenEis uniformly smooth,the normalized duality mappingjis single valued and norm to norm uniformly continuous on every bounded set.
A mappingS:E→Eis called a (q) -γ-strict pseudo-contraction if there is a constantγ >0 for eachy,z∈Eand for alljq(y-z) ∈Jq(y-z) such that
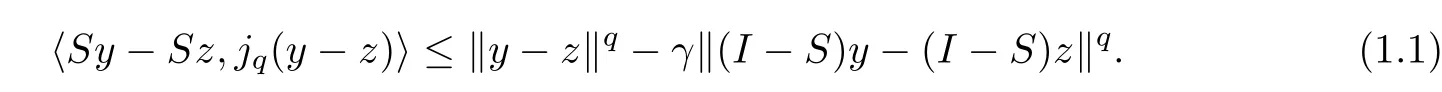
The set of fixed points of the mappingSis denoted by Γ(S);that is,Γ(S)={z∈E:Sz=z}.Clearly,(1.1) is equivalent to the following:
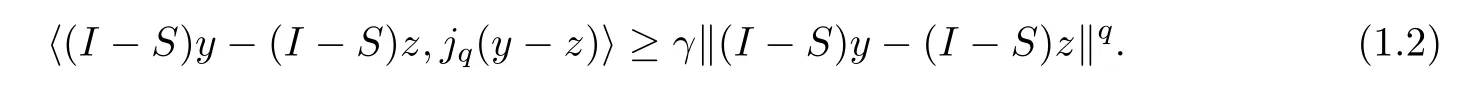
The following well-known theorem is the Banach contraction principle:
Theorem 1.1([2]) Suppose that (Y,d) is a complete metric space,and thathis a contractive mapping onY;that is,there is a constantρ∈(0,1) such thatd(h(y),h(z)) ≤ρd(y,z),?y,z∈Y.Thenhhas a unique fixed point.
Theorem 1.2([3]) Suppose that (Y,d) is a complete metric space,and thatφis a Meir-Keeler contraction (MKC for short) onY;that is,?∈>0,and there is a numberc >0 such thatd(y,z)<∈+cimplies thatd(φ(y),φ(z))<∈,?y,z∈Y.Thenφhas a unique fixed point.
Since the contractions are Meir-Keeler contractions,Theorem 1.2 is one of generalizations of Theorem 1.1.
Assume thatEis aq-uniformly smooth and strictly convex Banach space which admits a generalized duality mappingjq:E→E*.A mapping F :E→Eis said to be
(1)β-Lipschitzian,if there is a constantβ >0 such that
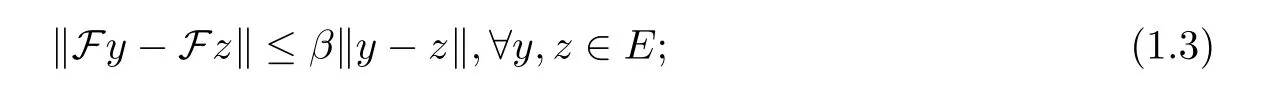
(2)δ-strongly monotone,if there is a constantδ >0 such that
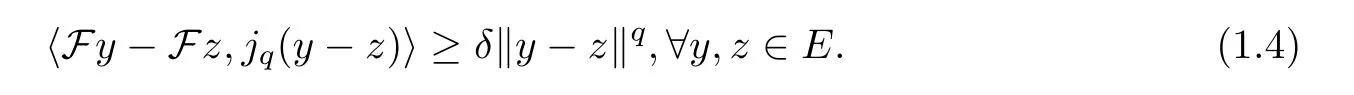
Definition 1.3Suppose that A is a strongly positive bounded linear operator in aquniformly smooth and strictly convex Banach spaceE;that is,there is a constant>0 such that
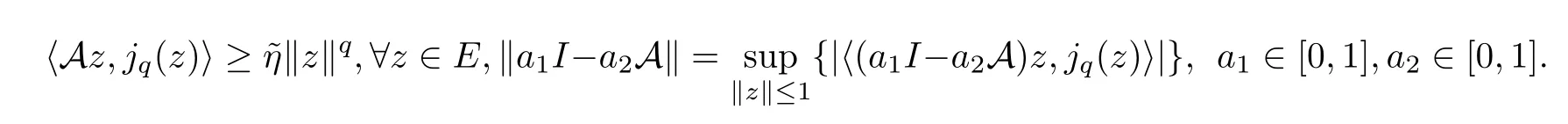
HereIis the identity mapping andjqis the generalized duality mapping.
Remark 1.4By the definition of A,we can know that A is a ‖A‖-Lipschizian and an-strongly monotone operator.
Suppose thatHis a real Hilbert space,and thatis a non-empty closed convex subset ofH.
In 2010,Jung [4] proposed the following method: for aγ-strict pseudo-contractionS:~D→Hsuch that Γ(S)≠? andx1=x∈~D,
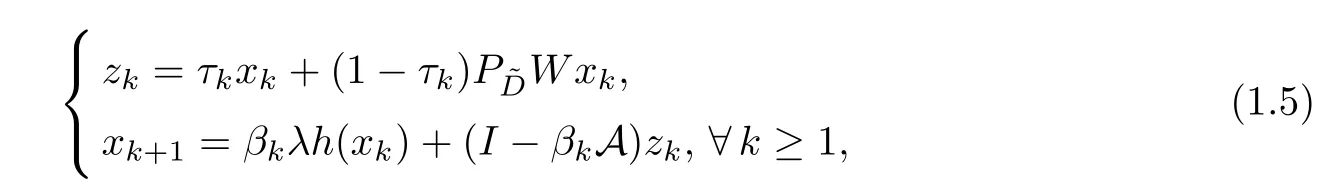
whereW:→His a mapping given byWx=γx+(1 -γ)Sx,and {βk} and {τk} ?(0,1)are sequences which hold,and 0<lim infk→∞τk≤≤b <1 for the constantb∈(0,1).He obtained that the sequence {xk} generated by (1.5)converges strongly to a fixed point ?xofS,which uniquely solves the variational inequality,z∈Γ(S).
Recently,Tian [5] introduced the iterative algorithm
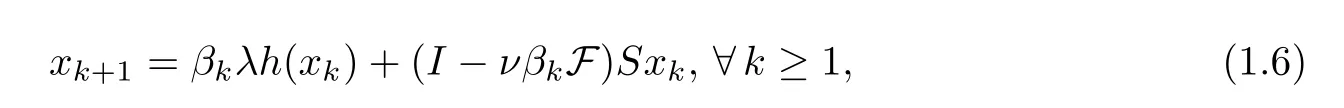
whereSis a non-expansive mapping onHsuch that Γ(S)≠?,F is aβ-Lipschitzian and aδstrongly monotone operator,{βk} ?(0,1) is a sequence which satisfiesHe proved that {xk} given by (1.6) converges strongly to a point ?xin Γ(S),which uniquely solves the variational inequality,z∈Γ(S).
Very recently,Wang [6] proposed the following algorithm: forx1=x∈,
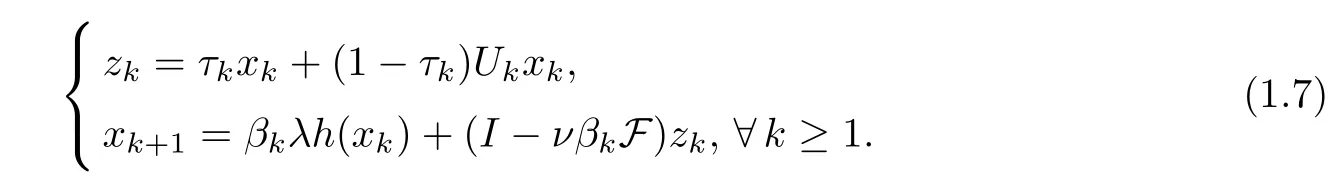
HereUkis a mapping given by (2.14),and F is aβ-Lipschitzian and aδ-strongly monotone operator such that,{βk} and {τk} ?(0,1).In Hilbert spaces,she obtained that if the parameters hold to certain conditions,then {xk} generated by (1.7) converges strongly to a common element of the fixed points of an infinite family ofγi-strict pseudo-contractions,which uniquely solves the variational inequality
Inspired and motivated by the above works,we introduce the following general iterative scheme: forx1=x∈E,
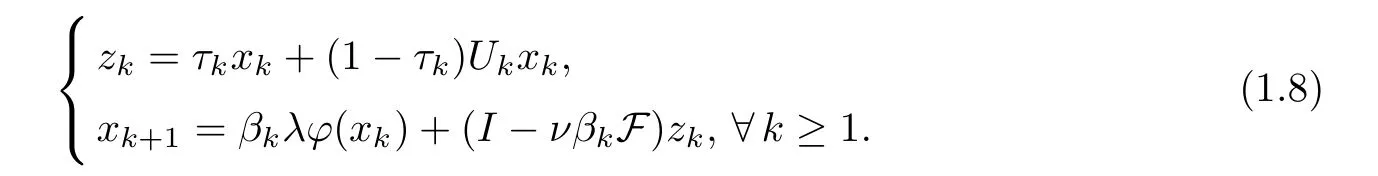
HereUkis a mapping given by (2.14),φis a Meir-Keeler contraction (MKC for short),and F is aβ-Lipschitzian and aδ-strongly monotone operator such thatWe will show that if the parameters hold to certain conditions (see (D1)–(D3) in Theorem 3.1),then {xk} given by (1.8) converges strongly to a common element of the fixed points of an infinite family ofγi-strict pseudo-contractions,which uniquely solves the variational inequalityOur results generalize the theories of Wang inself space[6] in the following two respects:
(i) we extend the results of Wang [6] from Hilbert spaces toq-uniformly smooth and strictly convex Banach spaces;
(ii) we extend the results of Wang [6] from a contractive mapping to a Meir-Keeler contraction (MKC for short).
The rests of this work is organized as follows: in the next section,we introduce the notations and preliminary results upon which we rely.In the final section,we study the convergence of the proposed methods.
2 Preliminaries
In this part,we mainly recall some lemmas which are useful for proving our main ideas.
Lemma 2.1([7]) Givenq >1,whereEis aq-uniformly smooth space,there is a constantDq>0 such that
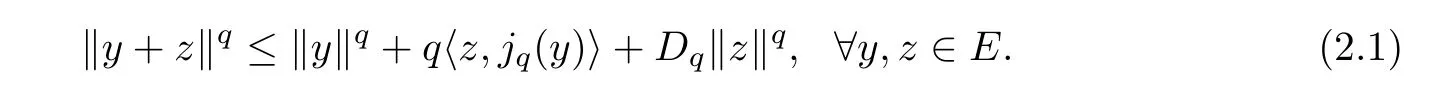
Lemma 2.2([8]) Suppose thatEis a Banach space,and thatDis a convex subset ofE.Ifφ:D→Dis an MKC,then for everyε >0,there is a numberc∈(0,1) such that
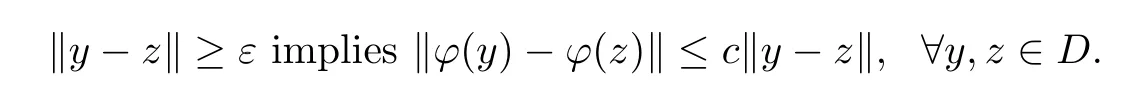
If,for any sequence {zk} in a Banach spaceE,zk?implies
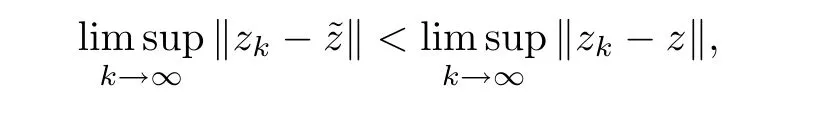
then ?z∈Ewith.ThenEsatisfies Opial’s condition [9].Banach spaces which satisfy Opial’s condition are all spaceslp(1<p <∞) and Hilbert spaces.However,Lp[0,2π] with 1<p≠2 cannot satisfy Opial’s condition.It is well-known that ifEadmits a weak sequentially continuous duality mapping,it satisfies Opial’s condition;see [10].
Lemma 2.3([11]) Suppose thatEis a reflexive Banach space which satisfies Opial’s condition,and thatDis a non-empty closed convex subset ofE.IfSis a non-expansive mapping fromDtoE,thenI-Sis demiclosed at zero;that is,zk?zand ‖zk-Szk‖ →0,and hencez=Sz.Moreover,Gu inself space [20] extended this conclusion from a non-expansive mapping to a asymptotic non-expansive mapping.
Lemma 2.4([12]) Suppose that F is aβ-Lipschitzian and aδ-strongly monotone operator in aq-uniformly smooth Banach spaceEsuch thatβ >0,δ >0,0<a <1 and 0<ν <minThenT=(I-aνF) :E→Eis a contractive mapping with a coefficient 1 -αθand
Suppose thatEis aq-uniformly smooth Banach space,and that F :E→Eis aβ-Lipschitzian and aδ-strongly monotone operator such thatβ >0,δ >0,andS:E→Eis a nonexpansive mapping.Letφ:E→Ebe an MKC with 0<a <1,0<ν <min.A mappingTaonEis then defined as
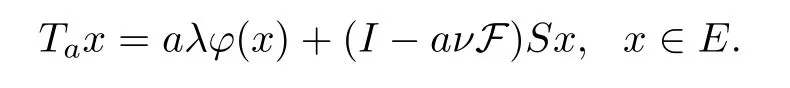
It is easy to get thatTais a contractive mapping.In fact,by Lemma 2.4,we obtain that
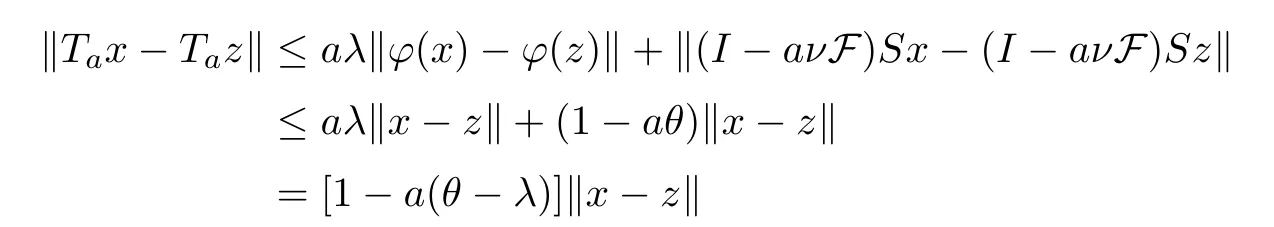
for allx,z∈E.Therefore,we have a unique pointxawhich is a unique solution of the fixed point equation
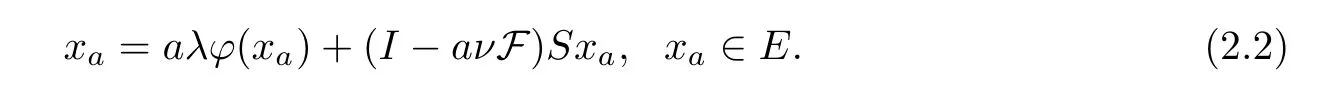
Lemma 2.5Suppose thatEis aq-uniformly smooth Banach space which admits a weak sequentially continuous duality mappingjq:E→E*.Given thatS:E→Eis a non-expansive mapping with Γ(S)≠? and thatφ:E→Eis an MKC,F is aβ-lipschitzian and aδ-strongly monotone operator onE.Let 0<λ <θ.Then,{xa} given byxa=aλφ(xa) +(I-aνF)Sxa(asa→0) converges strongly to a fixed pointpofS,which is a unique solution of the following variational inequality:
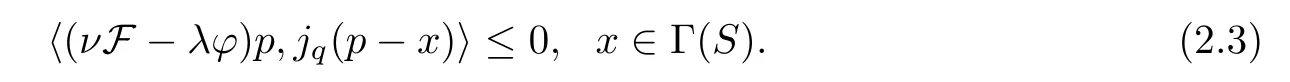
ProofAssume that both∈Γ(S) and∈Γ(S) are solutions of (2.3).Without loss of generality,we suppose that there exists a constantσsuch that.Therefore,from Lemma 2.2,there exists a constantcsuch that.By (2.3),we have that
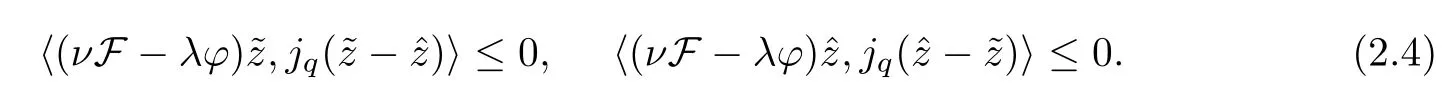
Adding up (2.4),we get that
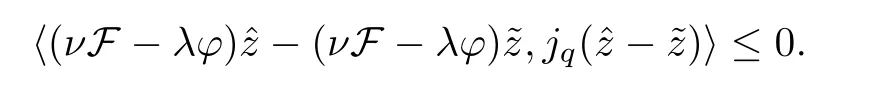
We observe that
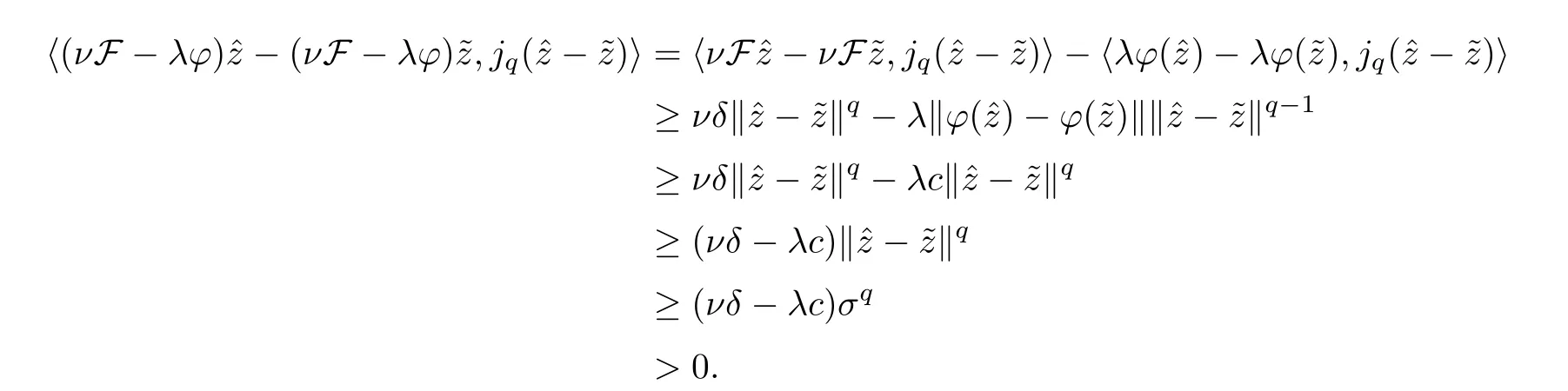
Notice that {xa} is bounded.In fact,fixz∈Γ(S) andσ1>0 for everya∈(0,1).When(‖xa-z‖ ≥σ1),from Lemma 2.2,we know that there exists a constantc1such that
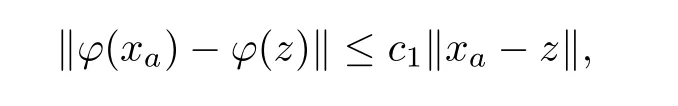
and thus,from Lemma 2.4,we get that
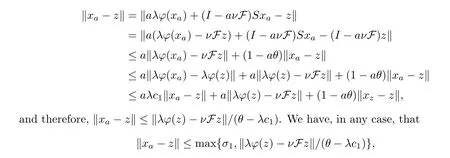
so {xa} is bounded.
Next,we show thatxa→(∈Γ(S)) asa→0.
Owing to the fact thatEis reflexive and that {xa} is bounded,there is a subsequence {xak}of {xa} such thatxak?z*.Byxa-Sxa=a(λφ(xa)-νFSxa),we get thatxak-Sxak→0 asak→0.In addition,becauseEsatisfies Opial’s condition,by Lemma 2.3 we havez*∈Γ(S).We show that

By the method of contradiction,there exists a constantσ0and a subsequence {xat} of {xak} such that ‖xat-z*‖ ≥σ0.From Lemma 2.2,there exists a constantcσ0such that ‖φ(xat)-φ(z*)‖ ≤cσ0‖xat-z*‖.We observe that
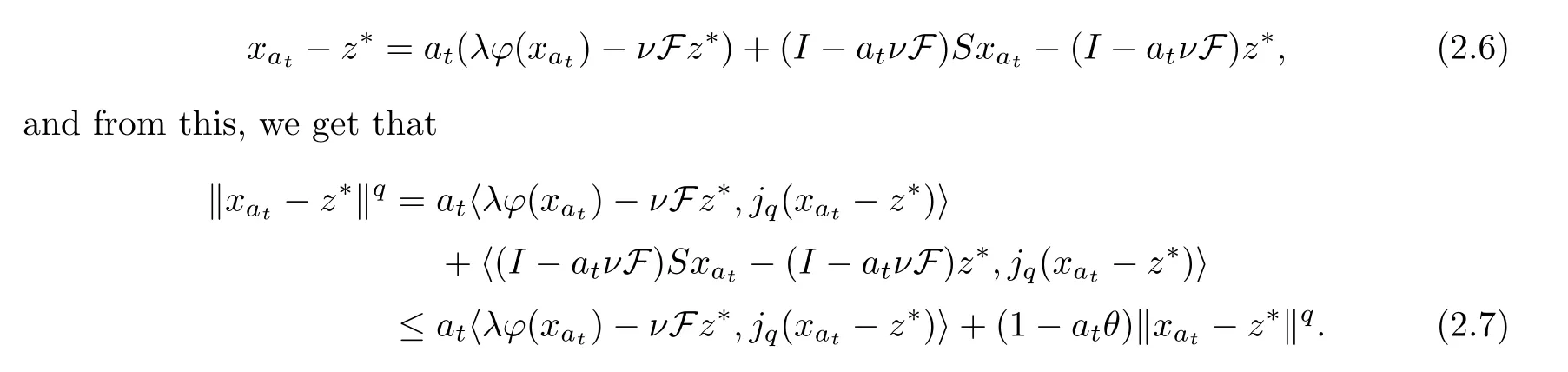
Thus,it can be seen that
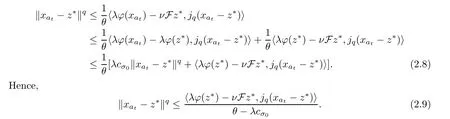
Using the fact that the duality mappingjq:E→E*is single valued and weakly sequentially continuous,from (2.9) we have thatxat→z*.This is a contradiction.Therefore,we obtainxak→z*.
Now,we show thatz*is a solution of the variational inequality (2.3).Because
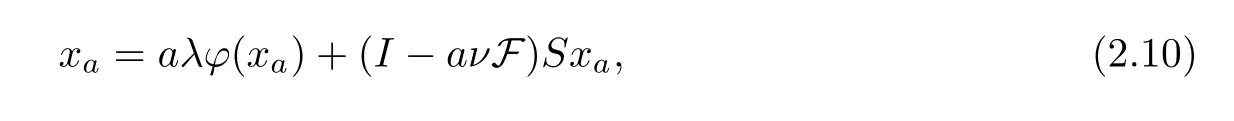
we get that
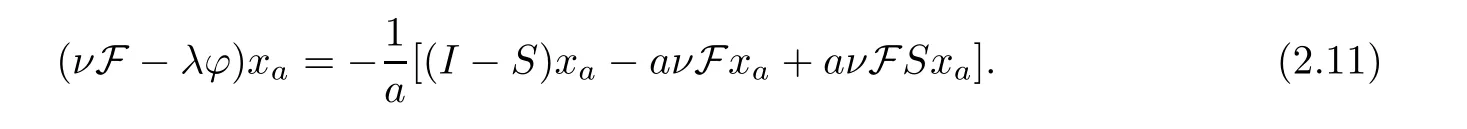
We notice that
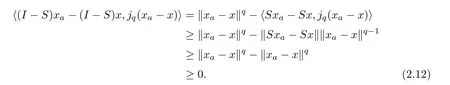
Therefore,forx∈Γ(S),
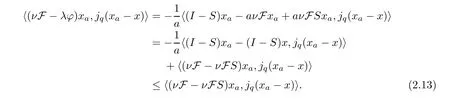
Now,let us replaceain (2.13) withak,and lettingk→∞,we observe that (νF -νFS)xak→(νF -νFS)z*=0 forz*∈Γ(S),so we get
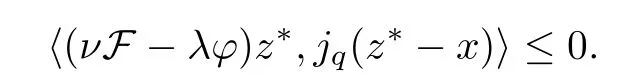
Thusz*∈Γ(S),which is a solution of (2.3).Therefore,z*=,by uniqueness.In conclusion,we have proved that every cluster point of {xa} (ata→0) equals,and hence,xa→asa→0. □
Lemma 2.6([13]) Suppose that {yk} and {zk} are bounded sequences in a Banach spaceE,and that {wk} is a sequence in [0,1] which adheres to the following condition:
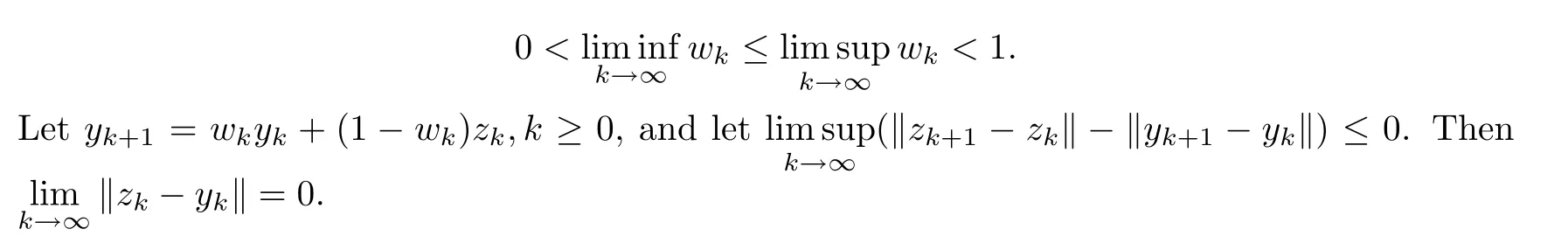
Lemma 2.7([14,15]) Suppose that {tk} is a sequence of non-negative real numbers which satisfies that
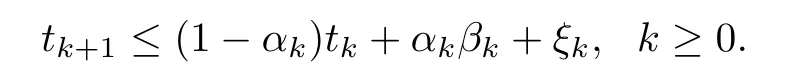
Here {αk},{βk} and {ξk} adhere to the following conditions:
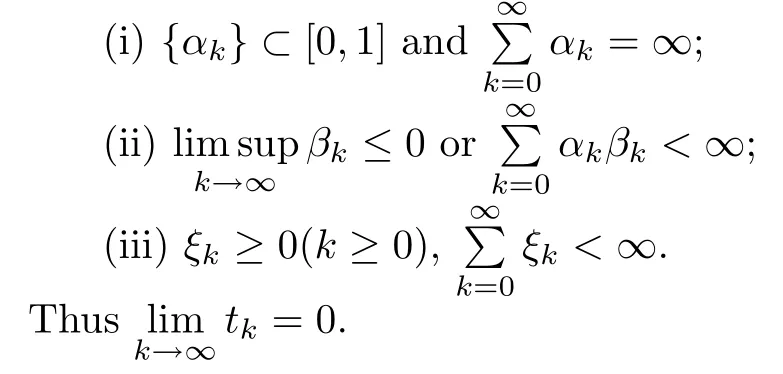
Lemma 2.8([16]) Suppose thatEis aq-uniformly smooth Banach space,thatDis a nonempty closed convex subset ofE,and thatS:D→Dis aγ-strict pseudo-contraction.Given a mappingS′onDwithS′z=rz+(1 -r)Sz,?z∈Dandr∈(0,ν],,soS′is called a non-expansive mapping,andF(S′)=F(S).
We consider the mappingUkgiven by

Here {λk} is a real sequence with 0 ≤λk≤1,,andSi:D→Dis aγi-strict pseudo-contraction withαi∈(0,min{1,.From Lemma 2.8,we can obtain thatis a non-expansive mapping such that.Therefore,it is easy see thatUkis a non-expansive mapping.
With respect toUk,we obtain the following important lemmas:
Lemma 2.9([17]) Suppose thatEis a strictly convex Banach space,and thatDis a nonempty closed convex subset ofE.Set thatis a family of infinite non-expansive mappings with,and that {λi} is a real sequence such that 0<λi≤m <1 for everyi=1,2,···.Then,for anyz∈Dandj∈N,exists.
By Lemma 2.9,a mappingU:D→Dis defined as follows:
Such a mappingUis said to be the modifiedU-mapping obtained byS1,S2,···,λ1,λ2,··· andα1,α2,···.
Lemma 2.10([17]) Suppose thatEis a strictly convex Banach space,and thatDis a nonempty closed convex subset ofE.Set thatis a family of infinite non-expansive mappings with,and that {λi} is a real sequence such that 0<λi≤m <1,?i≥1.Then
From Lemmas 2.8–2.10,we get that
Lemma 2.11([18]) Suppose thatEis a strictly convex Banach space,and thatDis a non-empty closed convex subset ofE.Set that··· are non-expansive mappings ofDinto itself such that,and thatλ1,λ2,··· are real numbers such that 0<λi≤m <1,?i≥1.Then,if G is any bounded subset ofD,we have that
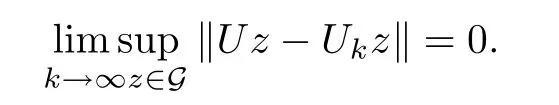
3 Main Result
Now we study the strong convergence results for an infinite family of strict pseudo-contractions in aq-uniformly smooth and strictly convex Banach space.
Theorem 3.1Suppose thatEis aq-uniformly smooth and strictly convex Banach space which admits a weak sequentially continuous duality mappingjq:E→E*.Set that {Si:E→E} is aγi-strict pseudo-contraction such that,and that {λi} is a real sequence with 0<λi≤m <1,?i≥1.Take that F is aβ-Lipschitzian and aδ-strongly monotone operator onEsuch that,and thatφis an MKC onEwith.Let {βk} and {τk} ?(0,1) be sequences which adhere to the following conditions:
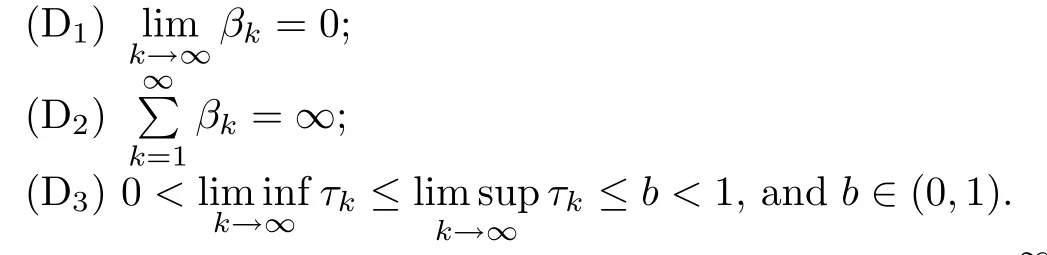
Then,{xk} generated by (1.8) converges strongly to,which uniquely solves the variational inequality
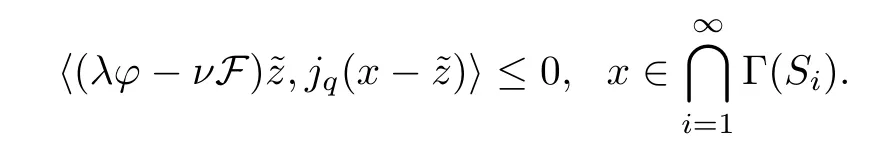
ProofThe rest of our proof consists of the following five steps:
Step 1We prove that {xk} is bounded.Actually,lettingx∈,it follows from(1.8) that
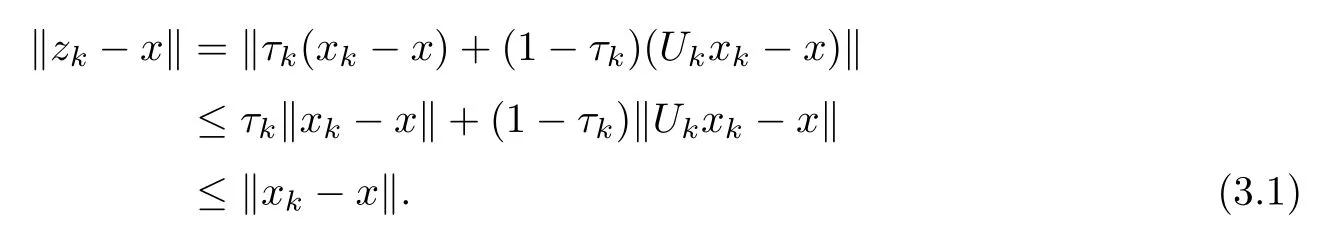
Thus,by (1.8),(3.1) and Lemma 2.4,we have that
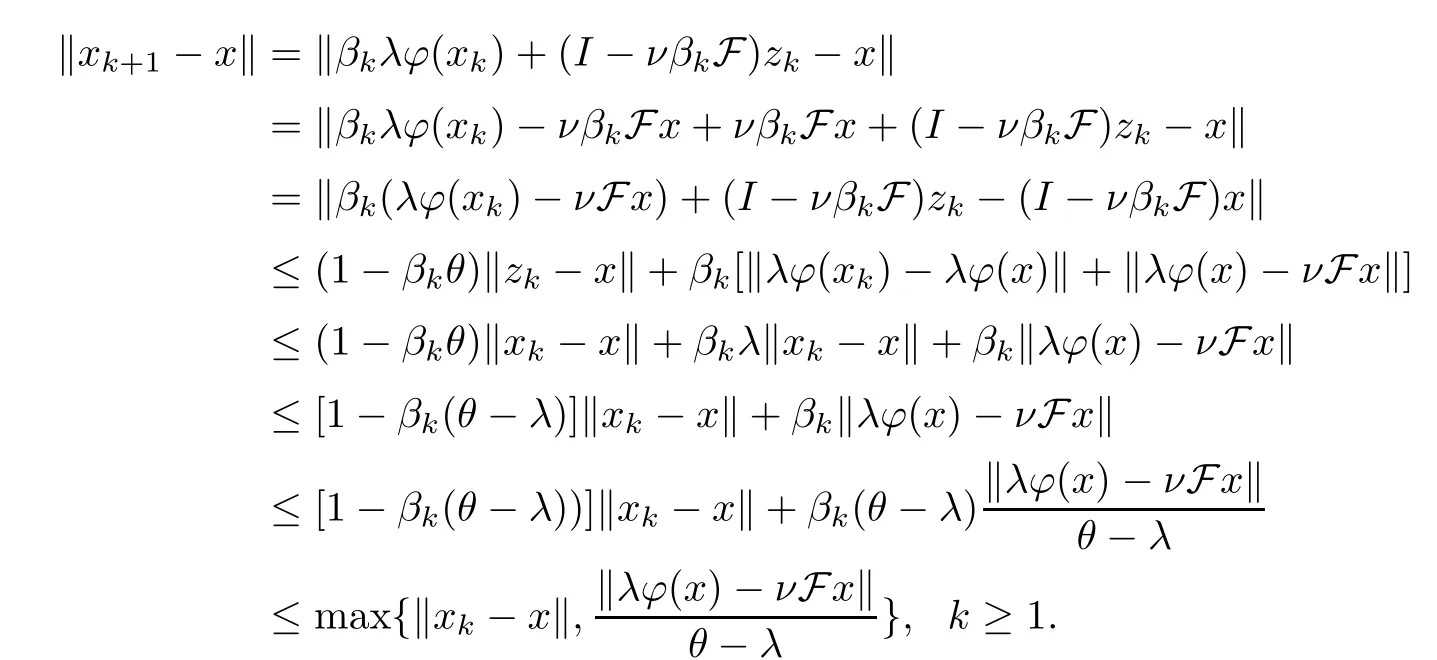
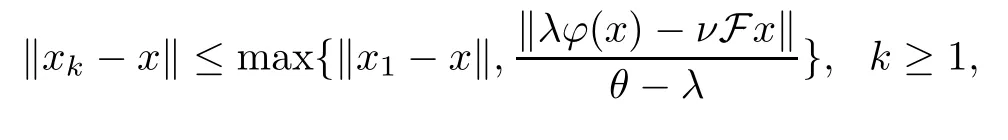
By induction,we get that so we have that {xk} is bounded.We also get that {zk},{Ukxk},{νFzk} andφ(xk) are all bounded.Without loss of generality,we suppose that {xk},{zk},{Ukxk},{νFzk},φ(xk) ?G,where G is a bounded set ofE.

Then,by (3.2),we get that
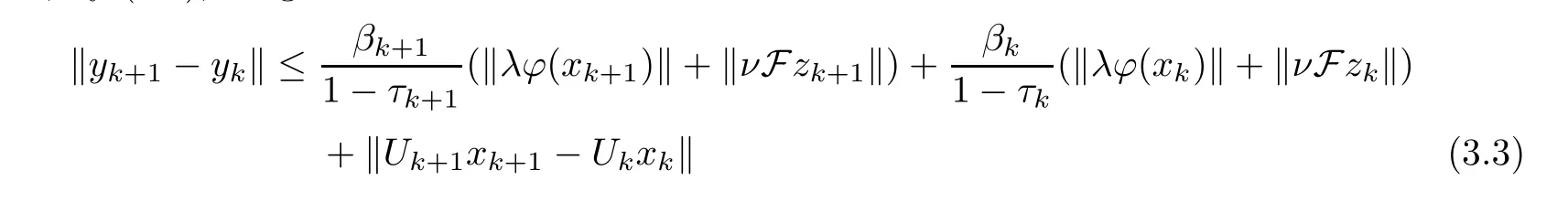
for allk≥1.
From (2.14),we obtain that
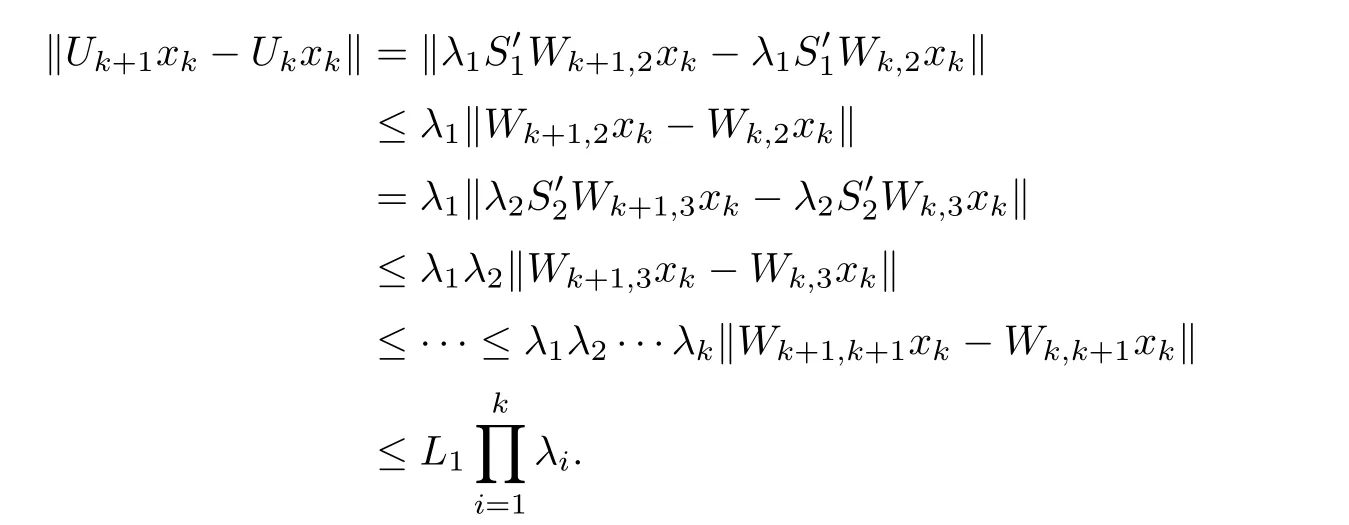
Here,L1≥0 is a constant which satisfies that ‖Wk+1,k+1xk-Wk,k+1xk‖ ≤L1,?k≥1.
Therefore,we obtain that
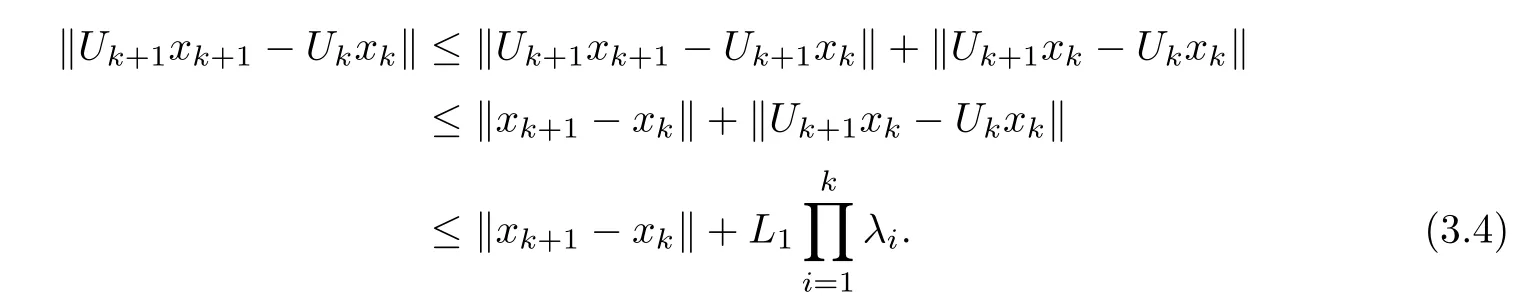
Putting (3.4) into (3.3),we get that
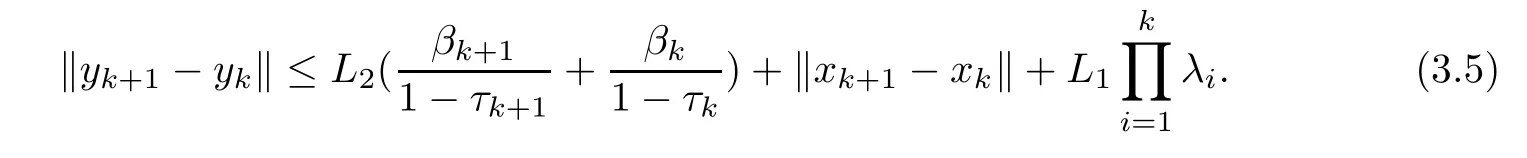
Here,L2=sup{‖λφ(xk)‖+‖νFzk‖,k≥1}.Then,by (3.5),we obtain that
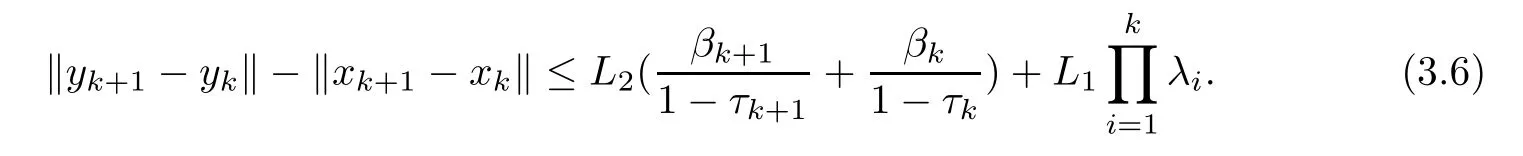
Noticing the conditions (D1),(D3),(3.6) and 0<λi≤m <1,we have that
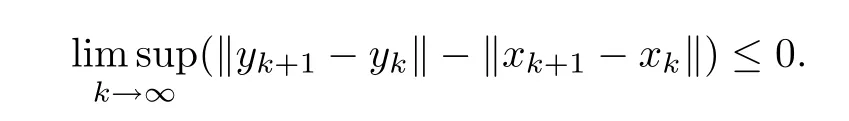
Therefore,from Lemma 2.6,we get that

From (D3) and (3.7),we obtain that
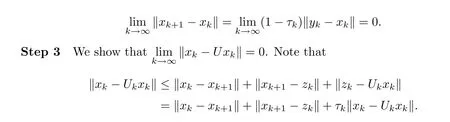
By Step 2,(D1) and (D3),we get that
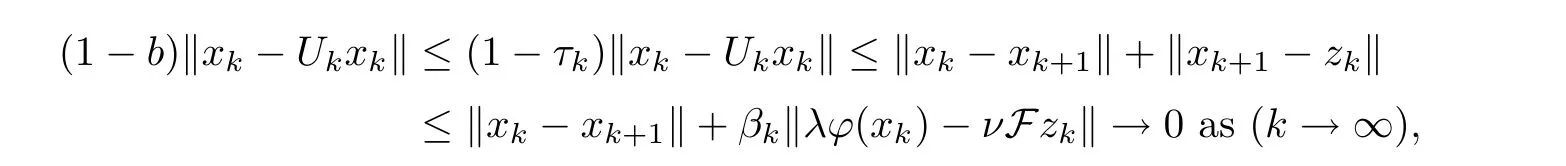
which means that
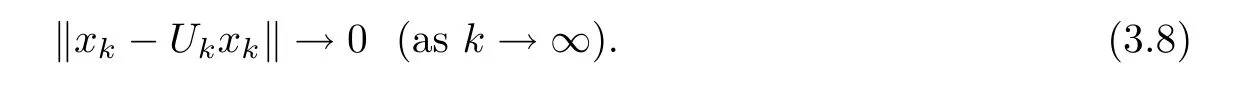
In addition,we know that
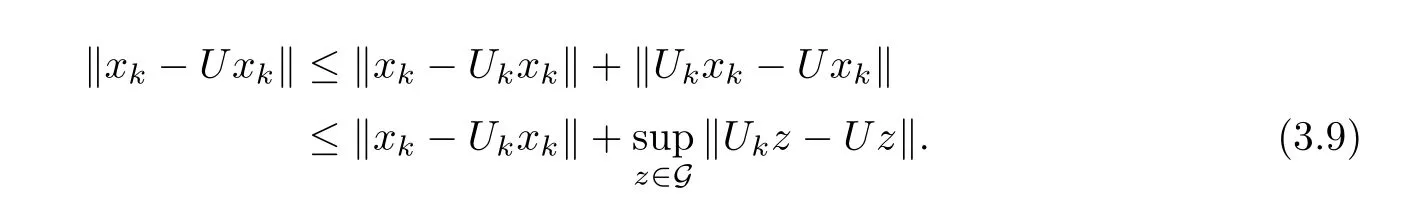
From (3.8),(3.9) and Lemma 2.11,we get that
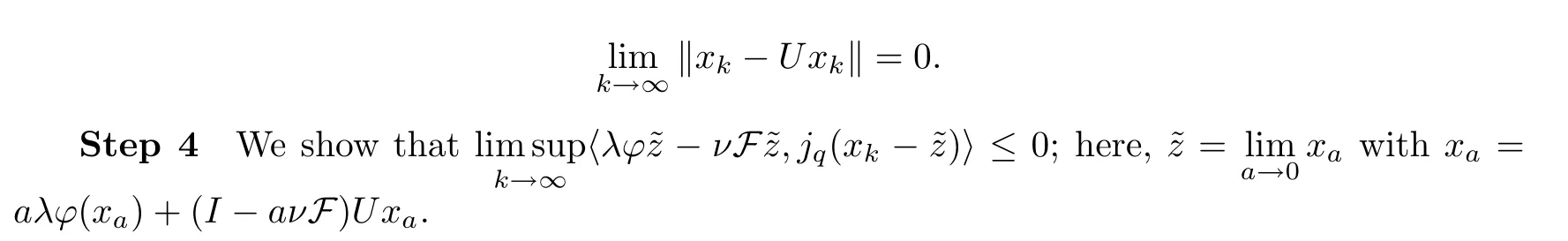
Due to the fact that {xk} is bounded,there is a subsequence {xkt} of {xk} which converges weakly tox,and such that.From‖xk-Uxk‖ →0,we obtain thatUxkt?x.SinceEadmits a weak sequentially continuous duality mapping,it satisfies Opial’s condition;see [10].By Lemma 2.3,we obtain thatx∈Γ(U).
Therefore,from Lemma 2.5 and the fact thatjqis a weakly sequentially continuous duality mapping,we have that
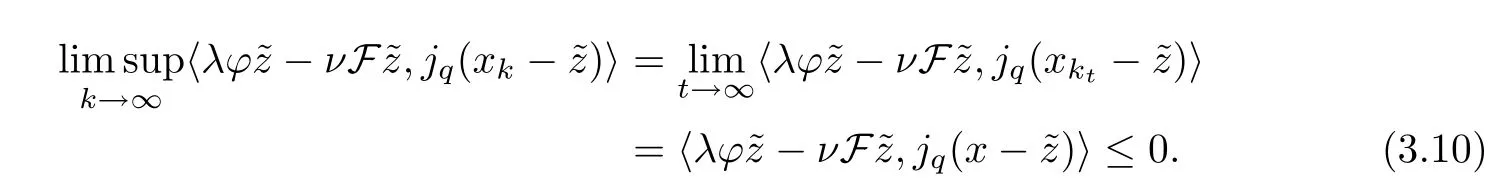
Step 5We prove that {xk} converges strongly to.By contradiction,there exists a constantσ0>0 such that
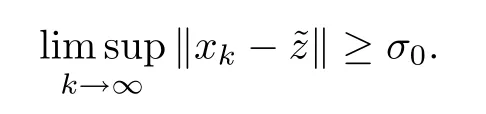
Case 1Fixσ1(σ1<σ0).Fix,for somek≥N∈N such that ‖xk-‖ ≥σ0-σ1,and for the otherk≥N∈N such that ‖xk-‖<σ0-σ1,set
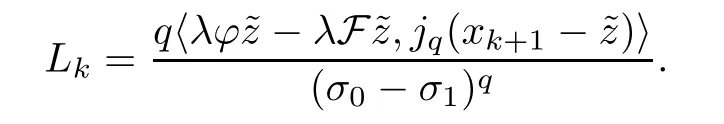
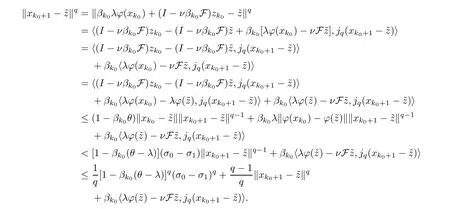
From Young’s inequality,we derive that
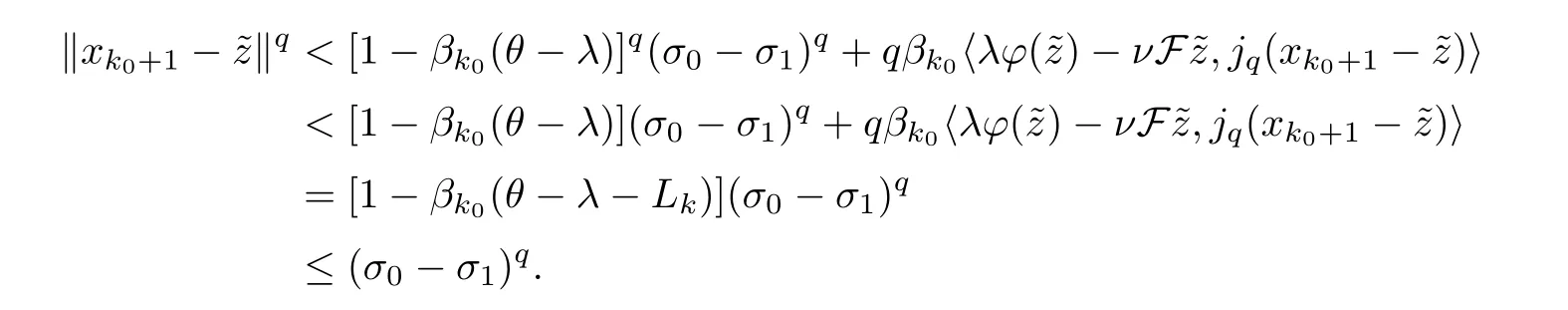
Thus,we obtain that
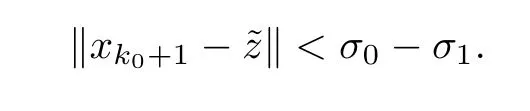
By induction,we have that
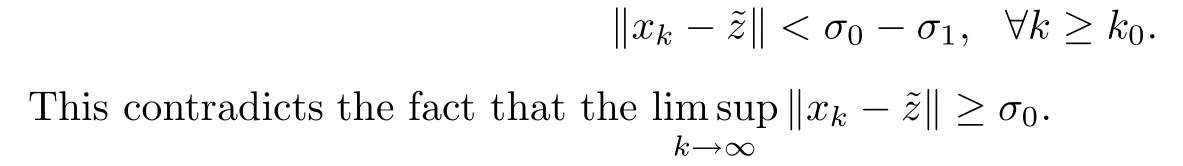
Case 2Fixσ1(σ1<σ0).Set ‖xk-‖ ≥σ0-σ1,?k≥N∈N.By Lemma 2.2,there exists a constantc∈(0,1) such that

Following on from (1.8),we get that
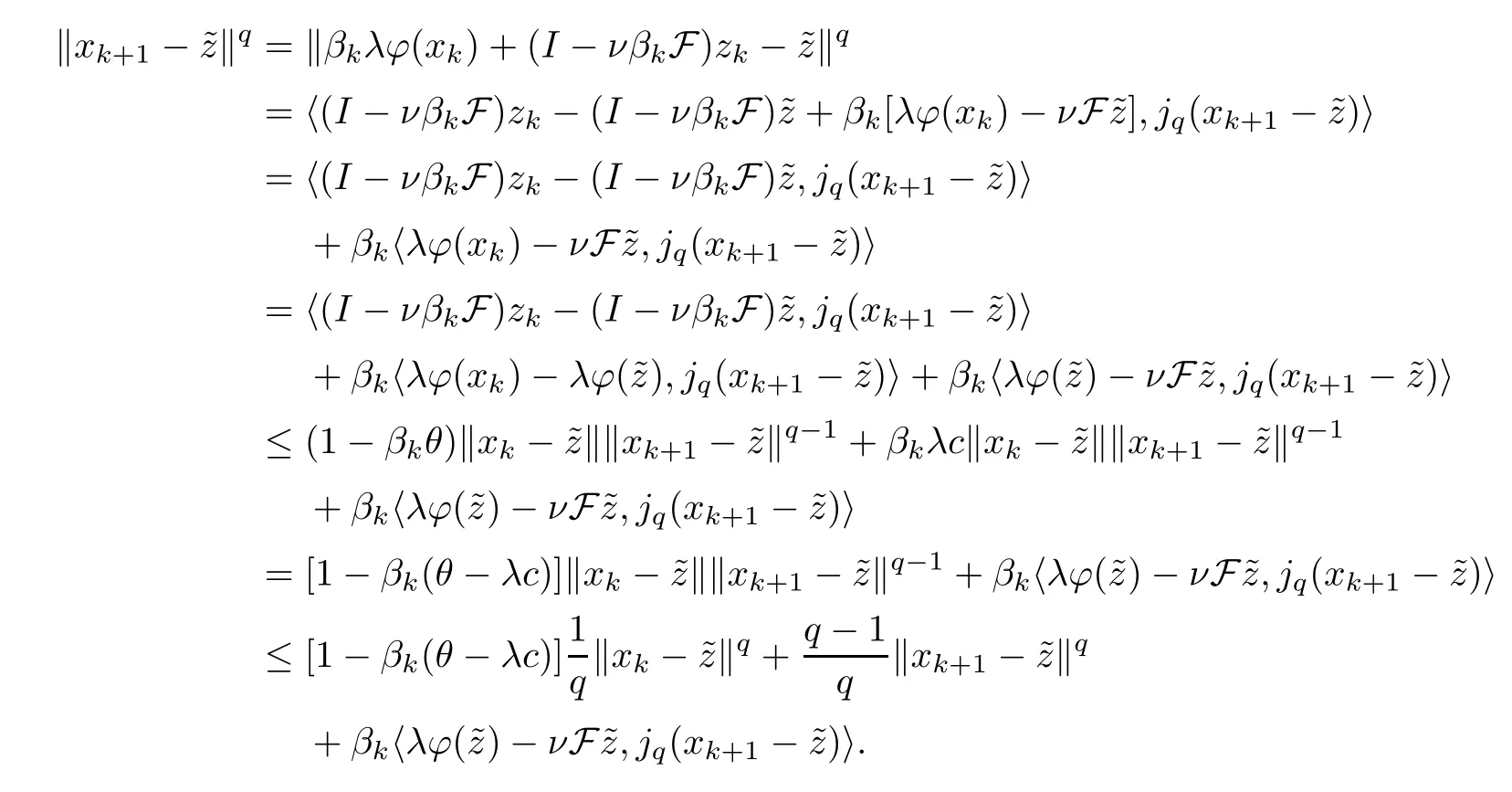
From Young’s inequality,we derive that

Lemma 3.2([19]) Assume thatEis aq-uniformly smooth Banach space which admits a weak sequentially continuous duality mappingjq:E→E*.Given thatS:E→Eis a non-expansive mapping such that Γ(S)≠? and thatφ:E→Eis an MKC,A is a strongly positive bounded linear operator with a coefficientθ >0.Suppose that 0<λ <θ.Then the sequence {xa} given byxa=aλφ(xa)+(I-aA)Sxa(asa→0) converges strongly to a fixed pointofS,which is a unique solution of the variational inequality
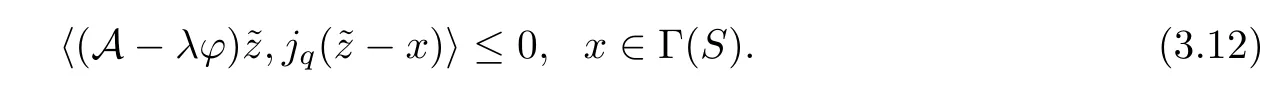
When F reduces to a strongly positive bounded linear operator A andν=1 in (1.8),we can obtain the following results:
Corollary 3.3Assume thatEis aq-uniformly smooth and strictly convex Banach space which admits a weak sequentially continuous duality mappingjq:E→E*.Suppose that{Si:E→E} is aγi-strict pseudo-contraction such thatand that {λi} is a real sequence such that 0<λi≤m <1,?i≥1.Set that A is a strongly positive bounded linear operator onEwith a coefficient 0<~η <1 and thatφis an MKC such that 0<λ <.Let{αk} and {βk} ?(0,1) be sequences which adhere to the conditions (D1),(D2) and (D3).Let{xk} be a sequence defined byx1=x∈Eas follows:
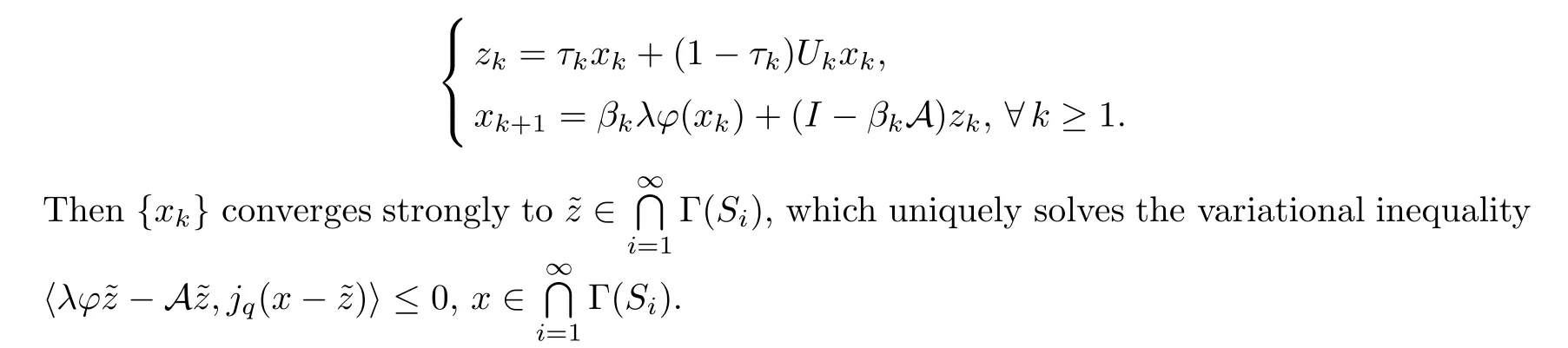
ProofBy the same steps as those used to prove Theorem 3.1,and replacing Lemma 2.5 with Lemma 3.2 in Step 4,we easily get the results of Corollary 3.3. □
 Acta Mathematica Scientia(English Series)2022年5期
Acta Mathematica Scientia(English Series)2022年5期
- Acta Mathematica Scientia(English Series)的其它文章
- RELAXED INERTIAL METHODS FOR SOLVING SPLIT VARIATIONAL INEQUALITY PROBLEMS WITHOUT PRODUCT SPACE FORMULATION*
- PHASE PORTRAITS OF THE LESLIE-GOWER SYSTEM*
- A GROUND STATE SOLUTION TO THE CHERN-SIMONS-SCHR?DINGER SYSTEM*
- A NON-LOCAL DIFFUSION EQUATION FOR NOISE REMOVAL*
- BLOW-UP IN A FRACTIONAL LAPLACIAN MUTUALISTIC MODEL WITH NEUMANN BOUNDARY CONDITIONS*
- POSITIVE SOLUTIONS FOR A KIRCHHOFFEQUATION WITH PERTURBED SOURCE TERMS*
