The Effects of θ on Stability in the θ-Milstein Method for Stochastic Differential Equations
MENG Xuejing(孟雪井) CHEN Lin(陳琳)
(1.School of Statistics and Mathematics,Hubei University of Economics,Wuhan 430205,China;2.Collaborative Innovation Center of China Pilot Reform Exploration and Assessment Hubei Sub-Center Hubei University of Economics,Wuhan 430205,China;3.School of Statistics,Jiangxi University of Finance and Economics,Nanchang 330013,China
Abstract:We consider the mean square stability of the θ-Milstein method for stochastic differential equations with local Lipschitz continuous coefficients.For θ∈[0,1/2),a counter example shows that the θ-Milstein method cannot reproduce the stability of the exact solution.By slightly strengthening the local Lipschitz condition,this paper concludes that the θ-Milstein method can capture the stability for θ∈[1/2,1].Finally,an example is presented to illustrate the result.
Key words:Stochastic differential equation;Mean square stability; θ-Milstein method;Local Lipschitz continuous
1.Introduction
Stochastic differential equations(SDEs)have attracted increasing interest in many different disciplines,particularly in biology,finance and engineering.However,analytic solutions of SDEs are not widely available,which is the main motivation for the development of numerical methods.Indeed,numerical methods for SDEs have recently returned many results,such as convergence[1],stability and dissipativity[2].Numerical stability plays an important role in numerical analysis,and the mean square exponential stability is an important topic in stability analysis.It implies almost sure exponential stability by the Chebyshev inequality and the Borel-Cantelli lemma[3].
This paper considers the numerical mean square stability of the following SDEs:
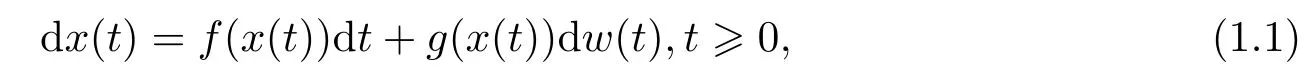
wherex(t)∈Rnand,for simplicity,x(0) is taken as a constant.We assume thatf(x):Rn →Rn;g(x): Rn →Rnare Borel measurable and thatw(t) is a Brownian motion defined on a complete probability space (Ω,F,P) with a filtration{Ft}t≥0.This filtration satisfies the usual conditions;it is right continuous and increasing,whileF0contains all P-null sets.We always assumef(0)≡g(0)≡0,for the stability focus of this paper.Thus,Eq.(1.1)admits a trivial solutionx(t)≡0.
Many numerical stability results were established under the global Lipschitz conditions[4-5].This excludes many important classes of stochastic systems,for example,the following wellknown stochastic Lotka-Volterra model): dx(t)=diag(x1,x2,···,xn(t))[(b+Ax(t))dt+x(t)dw(t)],herebandAare constant.In [3],it was shown that EM method cannot reproduce the stability of the SDEs without the linear growth condition.In recent years many people have studied the stability of the BEM as well as the theta method under superlinear growth conditions.[6-7]The Milstein-type method,as a higher-order method,can be seen as applying the stochastic Taylor expansion to the Euler-type method.The stability of the Milstein-type method has also received much attention in recent years.
There are many results for Milstein type methods,such as the backward Milstein[8],θMilstein[9],tamed milstein[10]and split-step Milstein[11].However,there are very few results of stability without the global Lipschitz and linear growth conditions.The aim of this paper is to examine the stability ofθ-Milstein method approximation with local Lipschitz continuous coefficients.
Apply theθ-Milstein method to Eq.(1.1).Given the step sizeh >0,letXkdenote the approximation tox(kh),withX0=x(0) and Δwk?w((k+1)h)-w(kh).Theθ-Milstein scheme then has the following form:
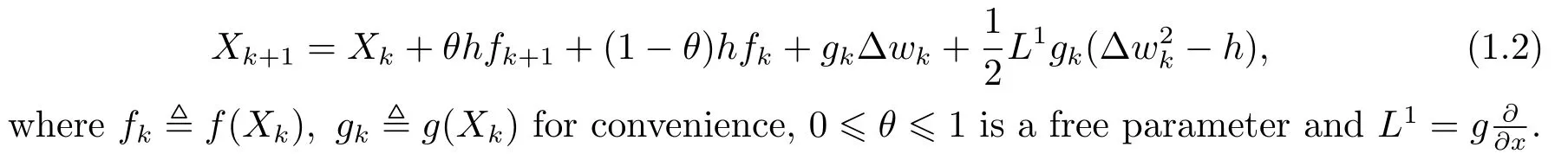
We should impose the following two assumptions on the coefficientsfandg:

for all thosex,y∈Rnwith|x|∨|y|≤j.
Assumption 1.2Letg(x) be a continuously differentiable function.There are three positive constants,a,b,K >0.And two non-negative constants,α,β,such that for allx,y∈Rn,
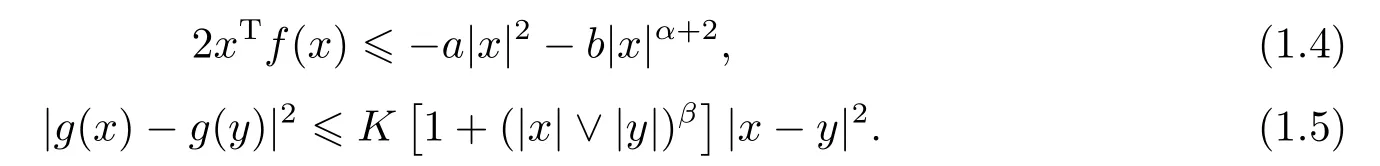
Obviously (1.5) is stronger than the local Lipschitz condition.Indeed,this condition is obtained by fixing the Lipschitz coefficientCj=K(1+jβ).
Unless otherwise specified,the following notations are used throughout this paper.Ifa,b∈R,a ∨bdenotes the maximum ofaandb,anda ∧bdenotes the minimum ofaandb.IfAis a vector or matrix,ATdenotes the transpose ofA,denotes the trace norm ofA.The inner product ofX,Y∈Rnis denoted by〈X,Y〉orXTY.For notational simplicity,the author uses the convention that const represents a generic constant,the values of which may be different for different appearances.
In the next section,we give the stability of the trivial solution to Eq.(1.1) and a counterexample,which shows that forθ∈[0,1/2),theθ-Milstein method cannot capture the stability of the exact solution.Section 3 discusses the stability of theθ-Milstein method forθ∈[1/2,1]under Assumption 1.2.The last section gives a numerical example and simulations to illustrate our result.
2.Stability of the Trivial Solution and a Counterexample
The following lemma plays an important role in this paper:
Lemma 2.1[12]Assume that 0 ≤K≤b,0<αand 0 ≤β≤α.Let

Then,for allx≥0,Kxβ+2-bxα+2≤Kρ(α,β)x2.
But if he could overcome and kill these two giants he should have his only daughter for a wife, and half his kingdom into the bargain; he might have a hundred horsemen, too, to back him up
The following theorem gives not only the existence-and-uniqueness but also the mean square exponential stability of the solution.
Theorem 2.1Let Assumptions 1.1,1.2 hold andα≥β.The constantρ1=ρ(α,β) is defined in Lemma 2.1.If

there exists a unique global solution to Eq.(1.1),denoted byx(t),with the property that
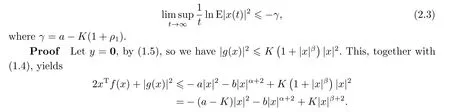
Byb >Kand Lemma 2.1,we haveKxβ+2-bxα+2≤Kρ1x2.These imply that 2xTf(x)+|g(x)|2≤-(a-K(1+ρ1))|x|2.Note thata-K(1+ρ1)>0.Choosing the Lyapunov function|x|2,by Theorem 4.4 in Chapter 4 of [13],the desired conclusion holds.
CHEN[4]gives a counter example to show that if the coefficients of the SDEs do not satisfy the linear growth condition,the stochasticθ-method cannot reproduce the stability of the exact solution whenθ∈[0,1/2).Thus,an interesting question is the following: Does theθ-Milstein method have a similar property?
Consider the following SDE:
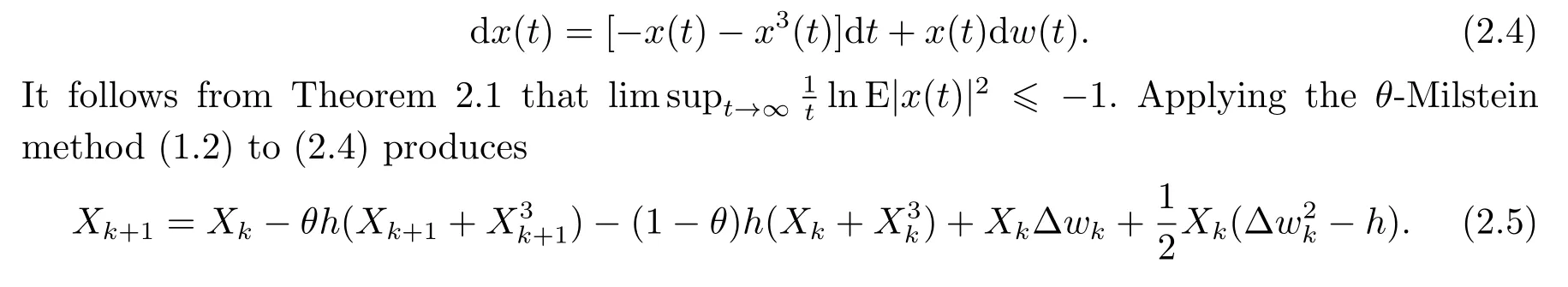
The following lemma shows that for anyθ∈[0,1/2) andh∈(0,1),{Xk}k≥0cannot preserve the stability of the exact solution of Eq.(2.4).

This lemma shows that ifθ∈[0,1/2),there is a non-zero probability that theθ-Milstein method will produce a numerical solution that increases at a geometric rate,even for arbitrarily small step sizes.This implies that for anyθ∈[0,1/2),this method is not stable in the moment.The next section shows that forθ∈[1/2,1],theθ-Milstein method will capture the stability of the exact solutions.
3.Stability Analysis of the Stochastic θ-Method
Lemma 3.1Assume thatn >0,α≥2β,ρ1=ρ(α,β),ρ2=ρ(α,2β)and that condition(2.2) holds.Let
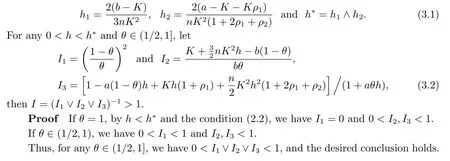
Theorem 3.1Let Assumption 1.2 and the condition (2.2) hold andα≥2β.Assume thatρ1,ρ2,h*andIis defined in Lemma 3.1 and that theθ-Milstein approximate{Xk}is defined by (1.2).Then,for anyh <h*,we have the following statements.
(i) Ifθ=1/2,then{Xk}is mean square asymptotic stable,


4.Numerical Example
A numerical example and its simulations are given in this section to illustrate our result.Consider the following scalar SDEs:
Example 4.1


By Theorem 2.1,the exact solutions of (1.1) are exponential mean square stable withγ=1/4.Choosingθ=0.6 andh=0.01,we can computeI ≈1.0022 andγ(h)≈0.2167.On the interval [0,10],we apply theθ-Milstein method (1.2) .The mean square of numerical solutions are shown in Fig.1.

Fig.1 The mean square of numerical solutions Xk
Remark 4.1We simulate the numerical solution based on the idea of [15],and the mean square numerical solution is estimated by averaging 1000 sample paths.The ordinate axis is logarithmic,and the graphs curves appear to be linear.This means that the numerical solutions tends to the trivial solution at an exponential rate.
- 應(yīng)用數(shù)學(xué)的其它文章
- 一類線性離散時(shí)間系統(tǒng)的預(yù)見控制器設(shè)計(jì)
- Global Boundedness to a Quasilinear Attraction-repulsion with Nonlinear Diffusion
- Trudinger-Moser Inequality Involving the Anisotropic Norm with Logarithmic Weights in Dimension Two
- 關(guān)于非齊次樹指標(biāo)m重馬氏信源的一個(gè)強(qiáng)極限定理
- 相依風(fēng)險(xiǎn)結(jié)構(gòu)下彈性ò休c金產(chǎn)品價(jià)?風(fēng)險(xiǎn)比較
- Superconvergence Analysis of Anisotropic Linear Triangular Finite Element for Multi-term Time Fractional Diffusion Equations with Variable Coefficient

