Bin Wang(王斌) and Jiping Huang(黃吉平)

1School of Mechanical and Power Engineering,East China University of Science and Technology,Shanghai 200237,China

2Department of Physics,State Key Laboratory of Surface Physics,and Key Laboratory of Micro and Nano Photonic Structures(MOE),Fudan University,Shanghai 200438,China

Keywords: flow control,metamaterials,hydrodynamic cloaks,drag reduction,liquid diodes

1. Introduction

Flow control can be divided into macroscopic flow control and microscopic flow control(i.e.,microfluidics). Macroscopic flow control usually includes drag reduction, lift enhancement, transition delay, separation postponement, turbulence augmentation,and noise suppression,among others.[1,2]For microfluidics, flows can be manipulated precisely with microscale devices, which are involved in the semiconductor industry, the micro-electromechanical systems (MEMS)field,lab-on-a-chip technologies,and bio-fabrication research,among numerous other areas.[3,4]Efficient flow control systems can not only save billions of dollars annually in fuel costs for air, land, and sea vehicles, but also enable industrial processes involving flow control to become more precise as well as more economically and environmentally competitive. Therefore, the ability to actively or passively manipulate the flow field to achieve desired changes according to human wishes undoubtedly becomes crucial. For example,the resistance of a traveling object (such as a car, submarine,airplane,etc.) is generally proportional to the square of the object’s velocity, and the power consumed is proportional to the third power of the velocity. Namely, whenever the velocity increases two times, the resistance will increase four times, and then the power consumption is increased to eight times. However,if an object is in a hydrodynamically perfect cloaking state,then its drag force can become zero in motion,and in turn this object will not need additional boosters and power consumption. Thus, zero energy consumption can be achieved,which would be very exciting.

The emergence of metamaterials of optical cloaks allows light or electromagnetic waves to propagate around an object as a fluid, leading to the cloaking of the object.[5,6]Consequently, it has inspired numerous studies on metamaterials in different fields, such as optics,[5,6]electromagnetics,[6,7]acoustics,[8,9]mechanics,[10,11]and thermodynamics.[12,13]However,how to achieve accurate manipulation of the flow remains a huge challenge because the Navier-Stokes equations governing fluid flow constitute a nonlinear set of equations,rendering studies of hydrodynamic metamaterials more challenging than those of other metamaterials, and consequently slower than the development of other metamaterials by many years. Fortunately,after these years of development,hydrodynamic metamaterials have gradually become an emerging hot research area.

To provide the readers with a clear understanding of the history, physical mechanisms, and future trends of hydrodynamic metamaterials,we would like to review the major milestones of hydrodynamic metamaterials. In this review, we first introduce the theory and experiment of various kinds of hydrodynamic cloaking metamaterials in porous media and non-porous media. Then, we introduce other hydrodynamic metamaterials beyond cloaking. Finally, we present an outlook on the development of this appealing field and raise the challenges to be addressed.

2. Hydrodynamic cloaking metamaterials

To understand the basic fundamentals of hydrodynamic metamaterials, we start with their governing equations. The continuity equation and Navier-Stokes equations for incompressible flows at steady state without the influence of body forces can be written as

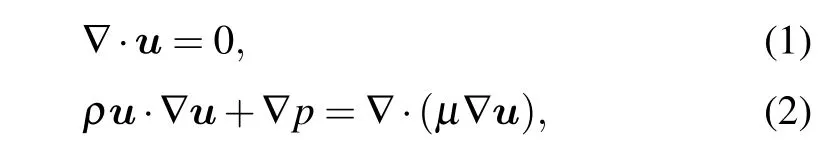
whereρ,μ,u, andpdenote density, dynamic viscosity, velocity vector,and pressure,respectively.

2.1. Hydrodynamic metamaterials in porous media

For creeping flows in porous media, the inertia termρu·?uin Eq.(2)can be neglected. Hence,equation(2)can be simplified to the Brinkman-Stokes equation[14]

Matching each term with Eqs. (1) and (5) subsequently provides us the fundamental equations for hydrodynamic transformation media[15]

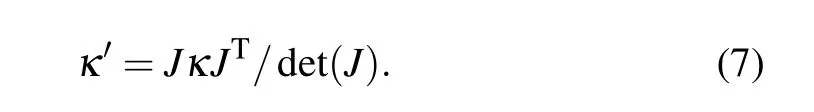
Similarly, hydrodynamic concentrators, hydrodynamic rotators, and hydrodynamic camouflage devices under creeping flows all can be obtained by coordinate transformation theory, as shown in Table 1. In addition, to extend metamaterials to the non-creeping flow circumstances,the stabilization of the hydrodynamic cloak in laminar-flow conditions[16,17]and the wave reduction resistance of the hydrodynamic cloak in turbulent-flow conditions[18]are successively studied. However,owing to the huge resistance of fluid flow in porous media,it is extremely difficult to provide a high Reynolds number for practical situations.

Table 1. The most common cylindrical hydrodynamic metadevices in porous media and non-porous media based on transformation hydrodynamics.

To further extend the hydrodynamic metamaterials to the area of convective thermal metamaterials, by coupling Eqs.(1)and(4)and energy transport equation,the authors in Refs. [19,20] successively studied convective thermal metamaterials from both steady-state and transient perspectives.After the extension of hydrodynamic metamaterials to the area of thermal metamaterials, numerous thermal metamaterials with various functions have been studied,[21-26]enabling the application of hydrodynamic metamaterials to be expanded from the area of nonlinear hydrodynamic metamaterials containing thermo-hydrodynamic coupling.

Since the above hydrodynamic metamaterials are obtained based on the theory of porous media, they cannot be applied in the environment without porous media. For this reason, numerous researchers have started to investigate hydrodynamic metamaterials in the non-porous media environment.

2.2. Hydrodynamic metamaterials in non-porous media

Inspired by the fact that magnetohydrodynamic (MHD)effects[27]can be used to eliminate vortices, an active magnetohydrodynamic metamaterial is studied.[28]This study demonstrates that the metamaterials can eliminate the wake behind the cylinder at a fixed volume force distribution under forced laminar flow over a wide range of Reynolds numbers.However, these magnetohydrodynamic metamaterials cannot achieve perfect cloaking. To establish a design theory for fabricating perfect hydrodynamic metamaterials, the authors in Ref.[29]first proved that equations(1)and(2)(neglecting the inertia term)in creeping flows satisfy the coordinate transformation invariance and established the transformation hydrodynamics. Because the fluid flow bounds in the boundary layer are rotational, the governing equations do not satisfy the coordinate transformation invariance. To provide a clearer and more concise proof,according to Ref.[30],under irrotationalflow idealization (i.e.viscous potential flows), equations (1)and(2)can be transformed into Laplace equations as

If we assume the flow is creeping flows, thenQ=p.Comparing Eq.(10)with Eq.(5)reveals that they are both in the form of Laplace’s equation. Obviously, we can similarly introduce the spatial coordinate transformation matrixJsuch that equations(9)and(10)from the virtual spacex(x,y,z)to the physical spacex＇(x,y,z)satisfy

Since equations (11) and (12) satisfy the coordinate transformation invariance,similar to the previous design of hydrodynamic metamaterials in porous media, we can choose different coordinate transformations and then use the transformation matrixJto calculate differentμ＇. Eventually,it is possible to design hydrodynamic metamaterials with different functions in non-porous media. For the hydrodynamic cloak in nonporous media, the parameters can be obtained from Eq. (13),as shown below[29](Fig.1(a)):

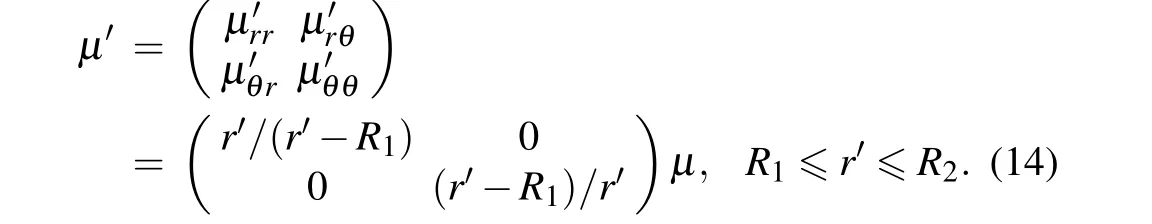
Inspired by the use of microfabricated arrays to steer,refract and focus the flow of biomaterials by Ref. [31], the hydrodynamic cloak for Hele-Shaw flows[32]is also experimentally fabricated.[29]It proves both theoretically and experimentally that the cloak can realize zero drag force.

Similarly, hydrodynamic concentrators can be designed by varying the coordinate transformation of the expansion and compression of different regions in the axial direction[33](Fig. 1(b)), hydrodynamic rotators can be designed by varying the coordinate transformation of the rotation angle[34](Fig.1(c)),and hydrodynamic camouflage devices can be designed by adding the corresponding camouflage based on hydrodynamic cloaks[35](Figs. 1(d) and 1(e)). These four hydrodynamic devices are summarized in Table 1. Noteworthily,when two coordinate transformations of hydrodynamic rotators and hydrodynamic concentrators are combined,a venturieffect rotating concentrator in varying arbitrary directions can be fabricated.[36]This study also reveals that changing the sequence of rotation and aggregation results in nonreciprocity of coordinate transformations,i.e.,rotational coordinate transformations are performed first,followed by aggregation transformations, compared with the opposite order of coordinate transformations, one of which exhibits a rotational hysteresis effect.

Since the shapes of objects in real life usually come in complex shapes,the authors in Ref.[37]designed a complexshaped cloak in Hele-Shaw flows by assembling different shaped cloaks, such as the square, triangular, and exemplary three-dimensional house-shaped cloaks. This study provides practical ideas for designing cloaks with different structures.In addition, the authors in Ref.[38]investigated the cloaking and drag reduction properties of cylinders, elliptic cylinders,vertical flat plates, and airfoils by using coordinate transformation theory, respectively. The study demonstrates that although the cloak designed by the coordinate transformation theory can achieve perfect cloaking only in the creeping Hele-Shaw flow situation, the drag reduction performance of the cloak remains excellent for the modest Reynolds number situation. It is remarkable that most of the above metamaterials obtained based on coordinate transformation theory are either obtained by linear coordinate transformation (transformation parameters are independent of other variables) or by background fluid being a single-phase flow. The investigation of hydrodynamic metamaterials in the case of nonlinear coordinate transformation and multiphase flow remains to be further explored, to which references[39,40]may provide inspiration.It is noticeable that when we introduce nonlinear coordinate transformation or multiphase flow, we need to pay attention to whether the original simplified equations (Eqs. (11) and(12)) are still applicable. For nonlinear problems, it is usually necessary to exploit a new theory. Subsequently,coupling the fluid dynamics and energy transport equations, the theory of transformation heat transfer in creeping flows is developed,which allows the design of different convective thermalmetamaterial devices,[41-43]and these findings will help to further explore nonlinear hydrodynamic metamaterials containing thermo-hydrodynamic coupling.

In order to promote the cloak to the non-creeping flows,the authors in Ref. [44] theoretically designed a cloak in the laminar flows by coordinate-transforming the density and the viscosity coefficient simultaneously. However, transforming the density means that the flow is treated as a compressible flow,so the simultaneous manipulation of density and viscosity coefficients is difficult to achieve from the current physical viewpoint,and perhaps the technology in the future could realize the simultaneous manipulation of both. Due to the limitation of anisotropy of metamaterials using coordinate transformation theory design, the authors in Ref. [45] used scattering cancellation method to theoretically and experimentally implement a metamaterial-free cloak by adjusting the height of the cloak. However, the method enables cloaking in twodimensional flows by sacrificing the flow in the third dimension, which is only valid at very low Reynolds numbers. Besides, the authors in Ref. [46] experimentally designed a microfluidic cloak that does not require metamaterials by using 3D printing and two inlet and outlet flow filters; and the authors in Ref.[47]used deep-reinforcement-learning to achieve hydrodynamic active cloaking, but these cloaks still fail to achieve perfect cloaking.

To homogenize the hydrodynamic cloak,[29]the authors in Ref. [35] then simplified the anisotropic inhomogeneous cloak to an anisotropic homogeneous cloak by using the integral median theorem and coordinate transformation theory.It is concluded that the drag force on the cloak in creeping flows becomes zero,and the cloak continues to exhibit remarkably strong drag reduction characteristics in laminar flows.Aiming to enable the cloak to be constant and extendable to non-creeping flows, the authors in Ref. [35] utilized the convection-diffusion-balance method, to solve Eqs. (9) and(10)analytically,and designed a microscale cylindrical cloak effective in a certain Reynolds number range (Re ≤42), the parameters of which are only related to the radius of the object and the cloak (μ2=(R22-R21)/(R22+R21)μb,μbis the background fluid viscosity coefficient), which greatly reduces the difficulty of cloak fabrication(Fig.2). Moreover,the study offers the possibility of realizing perfect cloaking by utilizing external fields(e.g.,temperature fields,external forces,and other methods). Subsequently, the authors in Ref. [48] achieved laminar hydrodynamic cloaking and hydrodynamic shielding at microscale from both numerically and experimentally by exploiting the electroosmotic flow-control method (Fig. 3).In addition, the method can achieve cloaking for arbitrarily shaped objects at the microscale.

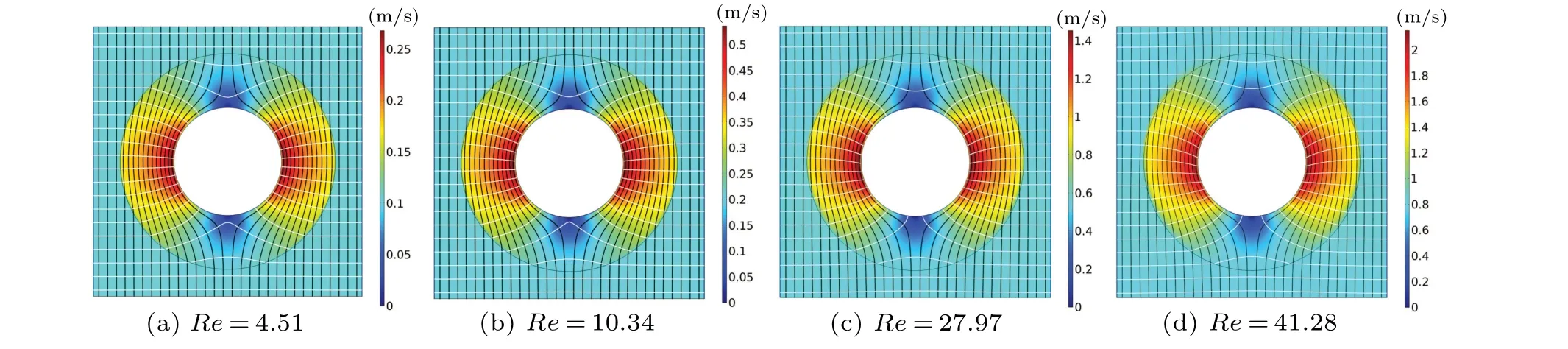
Fig. 2. Velocity distributions superimposed with streamlines (black lines) and isobars (white lines) of the hydrodynamic cloak at various laminar Reynolds numbers.[30]

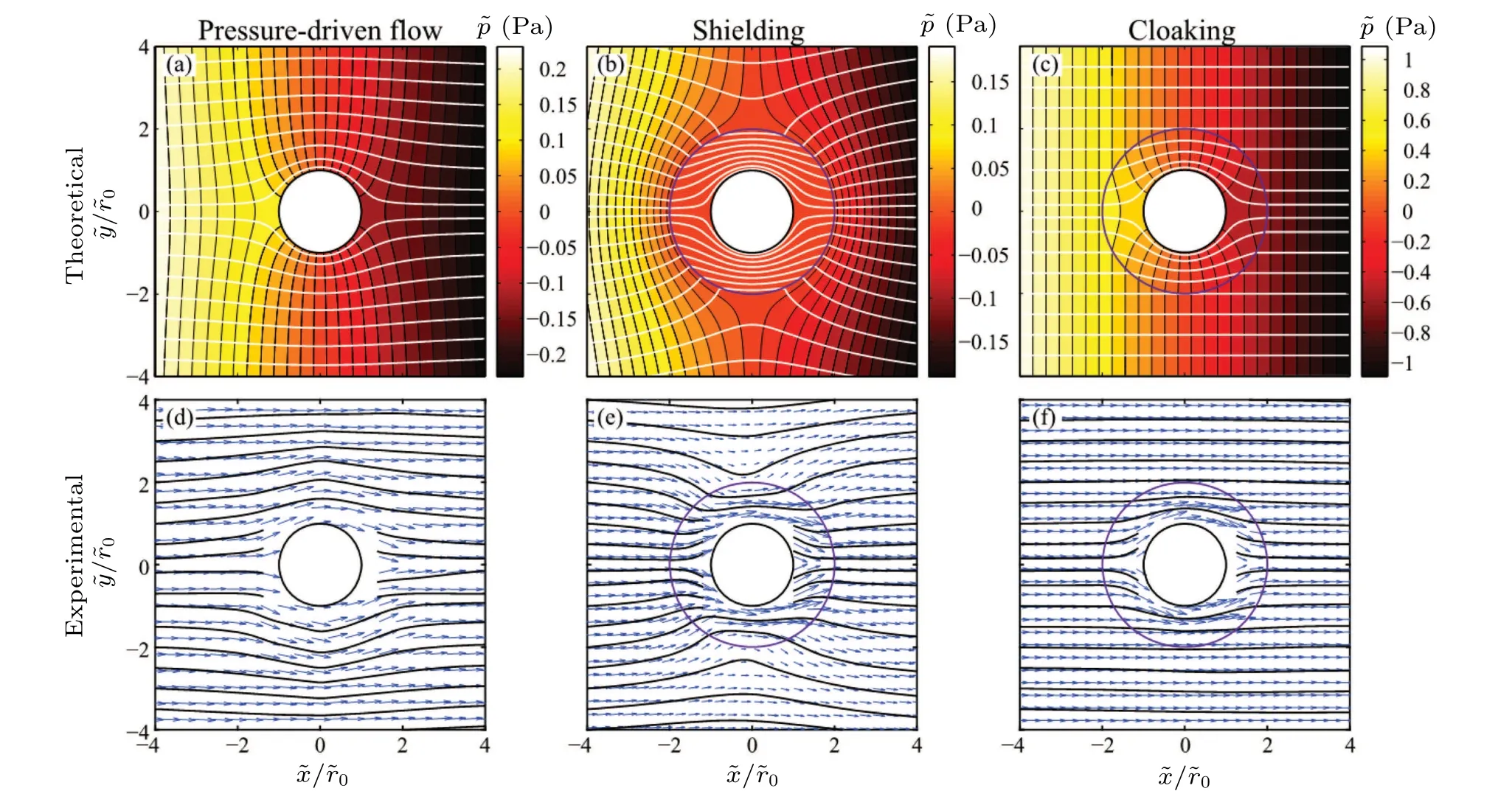
Fig. 3. Hydrodynamic cloaking and shielding in the presence of cylindrical objects.[48] (a)-(c) Theoretical pressure profile (color map) and streamlines(white lines)corresponding to(a)pressure-driven flow,(b)shielding,and(c)cloaking. (d)-(f)Experimental velocity fields(blue arrows)and resulting streamlines(black lines)corresponding to(d)pressure-driven flow,(e)shielding,and(f)cloaking.

It is noteworthy that although zero-drag hydrodynamic cloaks for non-creeping flows have been extensively studied,[30,44,48]these hydrodynamic cloaks are still mainly limited to low Reynolds numbers. How to improve the applicability of hydrodynamic cloaks to the high Reynolds numbers will be a very challenging direction in the future. Research in high Reynolds-number cloaking will not only enable us to achieve zero energy consumption cloaking motion, but also allow us to escape extreme natural disasters, such as typhoons, tornadoes, and tsunamis,etc. Besides, if we can design hydrodynamic metamaterials under high Reynolds numbers,we can even regulate these natural disasters and convert them into electrical energy for the benefit of mankind; alternatively,we can even regulate the climate as well as make climate weapons.[49-52]

3. Hydrodynamic metamaterials beyond cloaking

In addition to hydrodynamic cloaking metamaterials,numerous other hydrodynamic metamaterials are not intended for cloaking purposes, such as liquid diodes,[64,65,65-69]liquid gates,[70-72]among other aspects. Since these studies have already been reviewed in the relevant literature,we will not expand too much on them.For this reason,we selectively choose some typical hydrodynamic metamaterials for a brief introduction,hoping to inspire relevant studies.

3.1. Liquid diodes

The directional and passive transport of water droplets is a universal phenomenon in nature and plays a key role in a variety of practical applications in the fields of energy,materials, physics, chemistry, biology, and medicine.[53-63]Hence, numerous researchers have investigated bionic liquid diodes.[64-69]Similar to an electronic diode that can conduct current in the forward direction and block it in the reverse direction, a liquid device that can rectify liquids to flow in a directional manner can be treated as a “l(fā)iquid diode”. It is noteworthy that although traditional mechanical valves can also perform unidirectional transport functions,traditional mechanical valves are relatively bulky compared to liquid diodes.Moreover,unlike traditional valves,the primary regulation of liquid diodes is based on surface chemistry and topography,which is mainly used in microfluidics and biology. Besides,as opposed to electronic diodes that work on semiconductor materials by applying an external voltage, ideal liquid diodes are able to deliver liquids in a directional manner on a variety of materials regardless of the need for any external energy entry.[66]If liquid diodes could be built as liquid logic gates or even logic gate arrays, then liquid “l(fā)ogic circuits” could be built and their applications would be very exciting. Finally,the dependence of liquid diodes on surface topography leads to the existence of hysteresis resistance,which limits their transport distance and velocity significantly. How to overcome the hindering liquid self-transfer on the liquid diode will be an important challenge for it.

3.2. Liquid gates

Controllable fluid transport[73-76]plays an important role in multiphase separations,[77,78]energy harvesting,[79,80]microfluidics,[81]chemical analyses,[82,83]smart valves,[84,85]and other fields. In recent years, researchers have proposed an emerging liquid gating technology that uses liquids as dynamic structural materials,breaking through the limitations of a single solid material with properties such as anti-pollution,energy saving,and functional controllability,and has received considerable attention as a novel method to control fluid transport. The mechanism of this technology adopts the unique mobility of liquid as a dynamic“gate”to realize the“opening”and“closing”of the pore channel under certain pressure[70,71]or photothermal induction.[72]Meanwhile, due to the difference of interfacial tension between different kinds of transport fluids and gating fluids, it features specific gating thresholds for each type of transport fluid,so that transport control of different fluids under different conditions can be implemented. It is worth noting that liquid gates are affected by a variety of factors such as pressure,temperature and surface tension,among others,their stability and application is extremely demanding on the environment. Therefore,it will be a great challenge to design a stable liquid gate for a wide range of applications.

4. Summary and outlook

In this review,we introduce the recent progress of hydrodynamic metamaterials. The current studies of hydrodynamic metamaterials mainly focus on the use of coordinate transformation theory,analytical solution methods,machine learning,and external field control. However, previous studies are still mainly limited to the moderate Reynolds number range,which is mainly due to the Navier-Stokes equations are a nonlinear system of equations as well as the coordinate transformation theory is only valid in the creeping flow and shallow channel flows. Therefore,the current research scope of hydrodynamic metamaterials is still mainly in the field of microfluidics,and many aspects remain to be further explored. For this reason,we propose several prospects here.

(i)Since microfluidics has been extensively studied in the field of biofabrication,[86]related manipulation tools, such as optical,magnetical,electrical,mechanical,and combined manipulation techniques,may contribute in the future to diversify the fabrication of hydrodynamic metamaterials.

(ii) The hydrodynamic metamaterials in this review are mainly for the flow control of conventional fluids, and few hydrodynamic metamaterials have been reported for the design of some exotic fluids, such as supercritical fluids,[87-89]superfluids,[90-93]liquid metal,[94-97]metafluids,[98-100]multiphase flows,[101-103]among others. These exotic fluids may be very different from conventional fluids in terms of flow control because of their different fluid properties,which will probably provide directions for the development of the investigation scope of hydrodynamic metamaterials.

(iii)Because both the Stokes and Brinkman-Stokes equations at the steady state can be transformed into the Laplace equation,which is consistent with the steady-state form of the heat conduction equation. Therefore,many current innovative ideas for thermal metamaterials[104-109]can be applied to the design of hydrodynamic metamaterials. In addition,due to the control of thermal metamaterials mainly includes three basic forms of thermal conduction,thermal convection and thermal radiation,the development of the area of hydrodynamic metamaterials will help to reveal the manipulation mechanism of convective thermal metamaterials and further promote the development of thermal metamaterials.

(iv) Noteworthily, because of the zero-drag characteristic of hydrodynamic cloaks, one of the most challenging and attractive research directions in the future lies in the design of hydrodynamic cloaks in high Reynolds numbers. If the high-Reynolds-number hydrodynamic cloak is implemented,the human energy consumption will be significantly reduced,which is extremely beneficial to the development of aeronautics and astronautics, as well as to utilize or defend against typhoons,tornadoes,and other harsh natural environments.

(v)As a new branch of flow control,hydrodynamic metamaterials facilitate the understanding of fluid transport mechanisms which plays a critical role in understanding the mechanism of turbulent flows. Hence,comprehension to mechanism of turbulent flows will be promoted with the further advancement of hydrodynamic metamaterials. Because traditional fluid mechanics treats the dynamic viscosity as a fundamental property of a fluid,it may limit our understanding of fluid transport.In contrast,most of the parameters of hydrodynamic metamaterials are presented in the form of a tensor that varies with space, for example, the dynamic viscosity tensor exists in the limit values of infinity and zero. Understanding the dynamic viscosity or other parameters with space can deepen the understanding of the essence of fluid flows. Because turbulence can be understood mathematically and physically as the limit of fluid mechanics at zero viscosity. However,this limit comes as a singularity, because if we set the viscosity term directly to zero, we will not obtain turbulence using the Euler equation. This is because the viscous dissipation vanishes as the viscosity becomes smaller and smaller. Therefore, if we examine the nature of hydrodynamics with the perspective of asymptotically varying viscosity coefficients, it may help to reveal the nature of turbulence in the future. Perhaps this research direction,when flourished,could be called“metahydrodynamics”.

Acknowledgements

Project supported by Shanghai Science and Technology Development Funds (Grant No. 22YF1410600), the National Natural Science Foundation of China (Grant Nos. 11725521 and 12035004), and the Fund from the Science and Technology Commission of Shanghai Municipality (Grant No.20JC1414700).