吳德軍, 付家慧

(蘭州理工大學(xué) 理學(xué)院, 甘肅 蘭州 730050)

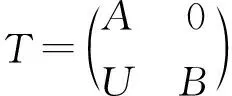
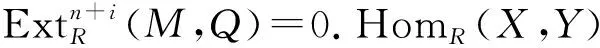
定義2[6]稱左R-模M為有限余表示模,如果左R-模M是有限余生成左R-模,并且對于任意的正合列0→M→L→N→0,若L是有限余生成模,則N是有限余生成模.

引理1[6]設(shè)0→M1→M2→M3→0是左R-模正合列.

1) 如果M1和M3是有限余表示左R-模,那么M2是有限余表示左R-模.

2) 左R-模的有限直和是有限余表示模當(dāng)且僅當(dāng)任意的直和項是有限余表示左R-模.

引理2[7]環(huán)R是左余諾特環(huán)當(dāng)且僅當(dāng)任意的有限余生成左R-模是有限余表示模.

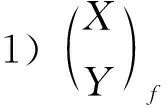
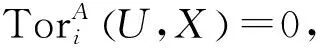
進(jìn)而由伴隨同構(gòu)知：

HomB(U?AX,Y)?HomA(X,HomB(U,Y))

2)i=0時,由1)可知.下證：i≥1時成立.存在正合列:

得到

又由引理4可知：

進(jìn)而得到

3)n=0時,由1)可知.下證：n≥1時成立.對X作投射分解有左A-模正合列：

…→HomA(Pm,HomB(U,Y))→

HomA(Cokerdm+1,HomB(U,Y))→

因為Pm為投射左A-模,所以

由1)知：

HomA(Cokerdm+1,HomB(U,Y))

進(jìn)而得到以下交換圖1.

圖1 交換圖

由引理5可知：

進(jìn)而有

所以n=1時成立.

當(dāng)n≥2時,有長正合列：

由2)和假設(shè)可知：

所以有

進(jìn)而有

由維數(shù)轉(zhuǎn)移可知：

因為n=1時已證得成立,所以有

又由維數(shù)轉(zhuǎn)移可知：

進(jìn)而得到了同構(gòu)式：

又因為

直積函子是加法函子,所以有

進(jìn)而有左T-模正合列：

進(jìn)而有左B-模正合列：

從而Q,P為有限余生成模.

如果Q為有限余生成左A-模,P為有限余生成左B-模,那么由定義1知對任意的單同態(tài)Q→∏ΛUλ,P→∏Λ′Vλ′存在正合列：

0→Q→∏ΛUλ→∏EUλ→0
0→P→∏Λ′Vλ′→∏E′Vλ′→0

從而有左T-模正合列：

證明因為AQ是有限余表示左A-模,所以存在正合列：0→Q→Q0→Q1,其中Q0,Q1是有限余生成內(nèi)射模.進(jìn)而存在左T-模正合列：

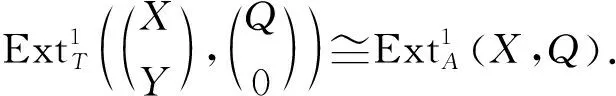
對于任意的有限余表示左B-模BP,由引理4有

下證.

0→HomB(U,P)→HomB(U,P0)→HomB(U,P1)

進(jìn)而有正合列：

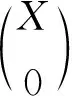
進(jìn)而有

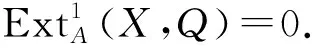
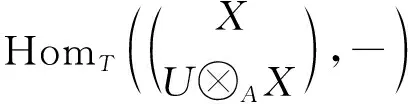
由引理4知：

又因為A為左余諾特環(huán),X是FC-投射左A-模,根據(jù)引理2可知Q是有限余表示左A-模,所以

進(jìn)而有

由引理5有

又由引理4有

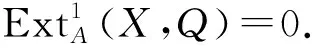
定理2考慮以下條件：

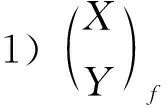
2)X是FC-投射左A-模,Cokerf是FC-投射左B-模且f是單同態(tài).

故X是FC-投射左A-模.下證：f是單態(tài)射.

對于有限余表示左B-模BW,存在正合列：

所以上正合列右正合得到滿同態(tài)g:

又因為

HomA(X,HomB(U,W))

HomA(X,HomB(U,W))?HomB(U?AX,W)

所以有交換圖2.

圖2 交換圖

進(jìn)而有f*是滿同態(tài).因為BW為內(nèi)射余生成子,所以f是單同態(tài).下證：Cokerf是FC-投射左B-模.

因為f是單同態(tài),所以存在正合列：

又因為

所以

進(jìn)而有Cokerf是FC-投射左B-模.

命題4設(shè)A為左余諾特環(huán),AU是有限表示左A-模.如果滿足以下條件：

2) FC-pd(BB)≤n-1,FC-pd(AA)≤n,FC-pd(BU)≤n-1.

那么有FC-pd(TT)≤n-1.

其中i≥2.因為AU是有限表示左A-模,根據(jù)文獻(xiàn)[6,30.5]有HomB(U,P)是有限余表示左A-模,所以有

其中i≥1.進(jìn)而有

其中i≥2.

因為FC-pd(BU)≤n-1,所以

其中i≥2.進(jìn)而有

其中i≥2.又因為FC-pd(BB)≤n-1,所以

其中i≥2.從而有FC-pd(TT)≤n-1.

由命題4可得

FC-pd(T2T2)≤n-1.