Shu-Xing Wang(汪書興) and Lin-Fan Zhu(朱林繁)

Hefei National Research Center for Physical Sciences at Microscale and Department of Modern Physics,University of Science and Technology of China,Hefei 230026,China

Keywords: integral cross section,electron scattering,x-ray scattering,BE-scaling method

1. Introduction

The demand of scattering data for atoms and molecules has been increasing in many fields[1–4]including astrophysics,plasma science, physical chemistry, radiation damage, etc.Accurate integral cross sections(ICSs)for electron impact excitations play an important role for modeling in the applied physics. For example, accurate excitation cross sections can produce reliable electron transport parameters for collisionalradiative models[5,6]and thus the quality of their output can be ensured. The models require not only the low-energy cross sections but also the high-energy cross sections. The low-energy case infers to low-temperature plasmas,which are widely spread in the Earth’s ionosphere, interstellar clouds,gaseous discharges and the edge of fusion plasmas.[7,8]The energy transfers from the electrons to atoms or molecules during inelastic collisions are the dominate cooling mechanism of thermal electrons. The heating source from external radiations and internal cooling generate the balanced Maxwell distributed electron energies. Furthermore, the electron impact excitation and following radiative decay or dissociation dominate the balance and radiation in a plasma. The highenergy cross sections,for example,are needed for applications in laser systems with amplifier cells pumped by high-energy electron beams. Thus,atomic and molecular ICS data over an extensive impact energy range are required for plasma modeling in different situations.

The ICS at specific impact energies could be determined by integrating the measured differential cross sections(DCSs)over the scattering angles. However, to generate an extensive ICS database via experimental measurements remains a challenge task. On the one hand, the DCSs at 0?and 180?are not accessible except for the rarely used magnetic angle changers.[9]The DCSs from froward and backward scattering in the crossed-beam measurements are usually obtained from extrapolating, which results in large uncertainties (usually higher than 30%)on the ICSs.On the other hand,the huge atomic and molecular database should be comprehensive,i.e.,the data for different targets with an extensive electron energy range are necessary. However, experimental measurements usually cost much and are sometimes problematic with absolute scales. The access to an answer can be that efficient theoretical calculations generate most of the data while experimental measurements constitute as a supplement. However,reasonable approximations are usually necessary for theoretical models to improve the feasibility or efficiency. These approximations would more or less introduce some inevitable errors.In addition,theoretical calculations are often restricted to high-energy(e.g.,perturbative Born-type)or low-energy(e.g.,non-perturbative close-coupling type) collisions. Therefore,accurate experimental measurements can serve as benchmarks for testing the theoretical models and computational codes.In other words, reliable experimentally measured atomic and molecular data with cross-checked methods are quite necessary not only for filling up the database but also for benchmarking theoretical calculations.

In the early years, pioneering electron collision experiments promoted the development of quantum scattering theory, including the well-known Bethe–Born approximation.The Bethe theory which describes the inelastic collisions of fast charged particles with atoms and molecules was reviewed by Inokuti.[10]The fruitful efforts in the past decades benefited from the improvements of experimental techniques and particle detection systems,such as the crossed-beam method,the position-sensitive detectors and the relative flow technique.It should be noted that the x-ray scattering experiments were limited by the extremely low cross sections and x-ray luminance in the early days but facilitated by the advanced third generation synchrotron radiations. The development of x-ray scattering method in atomic and molecular physics and its output have been recently summarized by Wang and Zhu.[11]At the present stage,both fast electron and x-ray scattering can be utilized to generate atomic and molecular data. The joint experimental and theoretical investigations not only deepen our understanding on the collision mechanisms but also fill up the atomic and molecular tables with credible data.

The requirements of the atomic and molecular ICSs are far from met due to the difficulty in evaluating accurate data over a wide energy range. Owing to the effort of Kim,[12,13]the BE-scaling method was developed and the ICS data for the electron-impact dipole excitations from the excitation threshold to an extended impact energy range could be produced with a satisfying accuracy. The gap between low-energy and high-energy electron scattering can thus be bridged since then.Nevertheless,the prerequisite of the BE-scaling method is the reliable generalized oscillator strengths (GOSs). Nowadays,reliable GOSs could be obtained via comparative studies of fast electron and x-ray scattering.[11]By following up with the Lassettre formula,the optical oscillator strength(OOS)could be determined by extrapolating the measured GOS to its limit at zero momentum transfer. The cross-check between the extrapolated OOS and photoabsorption or dipole(e,e)measurements could further eliminate possible systematic errors, i.e.,consistent OOS data will confirm the reliability of the measured GOS in turn. Moreover, the fitted curves are also required to integrate GOS over the whole momentum transfer region for Born cross sections and BE-scaled ICSs. The established BE-scaling method and its applications have been reviewed by Tanakaet al.[14]recently.

Here, the methods of fast electron and x-ray scattering experiments with atoms and molecules used in our group are reviewed. We take argon and carbon dioxide as examples to illustrate the experimental methods, data processing and the final results. The BE-scaled ICSs of the low-lying dipoleallowed states are reported for the first time from the crosschecked GOSs by electron and x-ray scattering methods. The paper is organized as follows. In Section 2, we present the experimental techniques and the data processing. The example results of argon and carbon dioxide are presented and discussed in Section 3. Finally, we give a general summary and outlook as a concluding remark in Section 4.

2. Methods

Electron scattering Electron energy loss spectroscopy(EELS) is generally used to measure the DCSs of atoms and molecules. The experiments are performed with an angleresolved electron energy loss spectrometer, consisting of an electron gun with a hemispherical monochromator, an interaction chamber for electron collisions and a position-sensitive detector following a hemispherical analyzer. The sketch view of the experimental setup is presented in Fig. 1. The rotatable analyzer enables the collection of scattering electrons at different angles and the multi-channel measurement enhances the collection efficiency for measurements at large scattering angles. During the measurement, the incident electron beam crossed with the gas sample diffused from a nozzle and the scattering electrons were collected by the analyzer and detected by the microchannel plate. For absolute measurement,relative flow technique was adopted by injecting helium and sample gas with a fixed ratio simultaneously. Thanks to the accurate experimental and theoretical GOSs of the 21S and 21P states for helium, the measured GOSs for samples can be normalized to an absolute scale with an improved accuracy. The crossed-beam technique with a gas nozzle offers a lower background pressure and a shorter interaction length in the collision region. Hence,the multi-scattering signals due to the pressure effect can be eliminated.

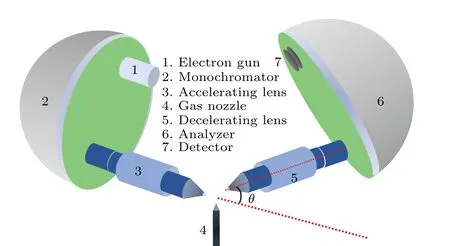
Fig.1. Sketch view of the electron energy loss spectrometer.

X-ray scattering Non-resonant inelastic x-ray scattering (NRIXS) was widely used in condensed matter physics while its applications with gaseous samples were limited by its extremely low cross sections. With the development of advanced detection techniques and third generation synchrotron radiations,NRIXS has been extended to atomic and molecular physics.[15–17]The sketch view of the NRIXS setup is presented in Fig. 2. The x-ray scattering experiments were performed at the BL12XU at the SPring-8 with an incident photon energy of about 10 keV.The high-pressure gas was sealed in a gas cell to enhance the scattering signals.The major advantage of NRIXS is that the first Born approximation(FBA)is always applicable for x-ray scattering but fails for electron scattering in some cases.[16,18,19]In other words, NRIXS can serve as a high-energy limit for fast electron scattering where the FBA should describe the scattering behaviors well. The comparative study can certainly point out the cases where the FBA fails for electron scattering and the resulted GOSs constitute a set of benchmark data.

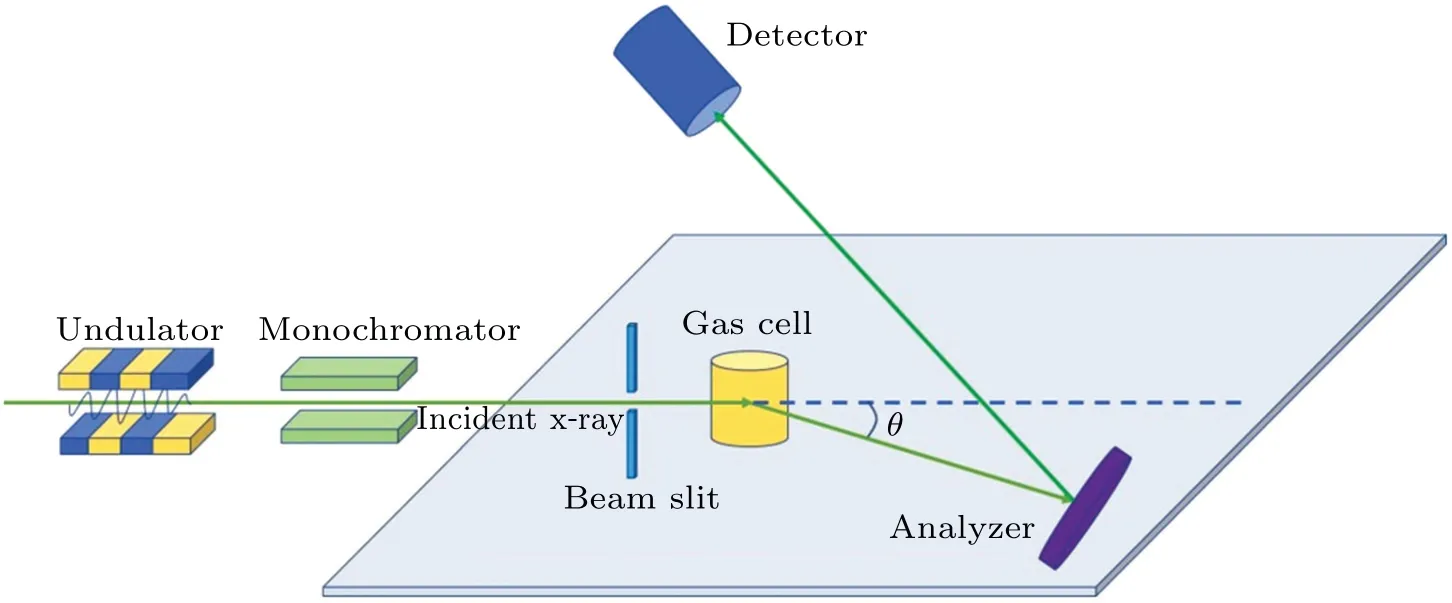
Fig.2. Schematic diagram of non-resonant inelastic x-ray scattering.

2.1. Data analysis

In the framework of the FBA,the measured DCSs of electron and x-ray scattering are related respectively with the GOS via

whereΨ0andΨnare the wave functions for the initial and final states whilerjis the position vector of thej-th electron.

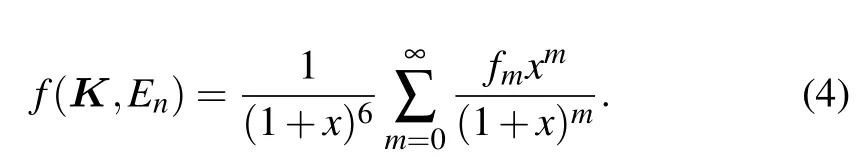
The measured GOS can be extended to its limit at zero momentum transfer by following up with the Lassettre formula[20,21]Here,x=K2/α2is the modified momentum transfer square with a fitted scaleα2. The intercept (f0) of the fitted curve comes to the corresponding OOS for a dipole-allowed transition.

The demand of the ICS data over a broad energy range was not satisfied until Kim[13]proposed the BE-scaling method based on the plane-wave Born models. The ability to produce reliable ICS data at low impact energies not only supplies abundant required data but also bridges the gap between low-energy and high-energy electron scattering. The equation was written as

3. Results

The joint electron and x-ray scattering studies with atoms and molecules have produced a lot of valuable data, including GOSs, OOSs and ICSs.[22–25]We will take atomic argon and molecular carbon dioxide as examples. The GOSs of the low-lying states for argon have been reported before.[19,26–28]Here we only present the extrapolated OOSs and BE-scaled ICSs for comparison with the available data in literature. The associated data for carbon dioxide of the low-lying features are also discussed. The typical electron and x-ray energy loss spectra of argon and carbon dioxide at selected angles are presented in Fig.3.The scattering experiments were performed at an incident electron energy of 1500 eV and an x-ray energy of about 10 keV, respectively. The energy resolutions are about 70–90 meV.

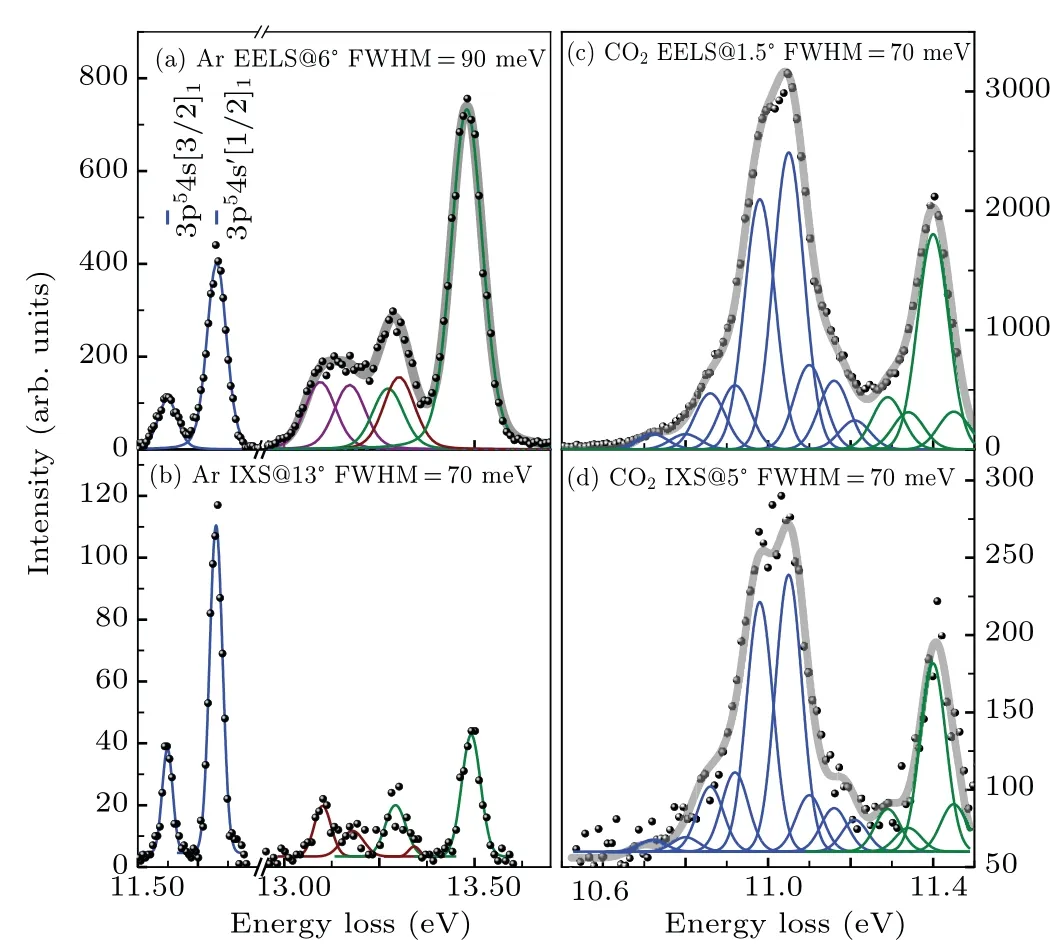
Fig. 3. The energy loss spectra of fast electron and x-ray scattering at selected angles. The dots are the measured data while the lines are the fitted curves. Note that the bold gray lines are the total fitted curves and the thin ones are for the isolated transitions.

3.1. Argon

The noble gas argon is widely distributed over the universe and also an important medium in gas electronics.Atomic data associated with electron or x-ray scattering processes are crucial for deriving the elemental abundance in the astrophysical observed spectra and for modeling in lowtemperature plasmas. The GOSs or the equivalent inelastic squared form factors (ISFFs) of the valence-shell excitations below 15 eV for argon were studied by both fast electron[19,26–28]and x-ray[29]scatterings. Note that the earlier experiments by Jiet al.[26]and Zhuet al.[27,28]were performed with gas cells while crossed-beam method with gas nozzle was adopted in the recent measurement[19]to improve the accuracy. In addition, theoretical approaches with the Hartree–Fock method,[30]random phase approximation with exchange (RPAE),[31]relativistic distorted wave (RDW),[32]eigenchannelR-matrix method,[33]etc,have also been applied in the calculations of oscillator strengths or cross sections for argon. The detailed comparisons between the experimental data and theoretical calculations have been made in the previous publications.[19,29]

The comparative study of electron and x-ray scattering suggested that the FBA is not applicable for the electron scattering aroundK2=1 a.u. of the 4s[3/2]1and 4s′[1/2]1states,even with the incident electron energy of 1500 eV.[19]In other words,the higher Born terms dominate the GOSs at the minimum in the electron scattering whereas theoretical calculations under the FBA can describe the x-ray scattering well.In order to evaluate accurate ICS data with the BE-scaling method, we pick up the x-ray scattering data and the recent electron scattering data away from the minimum for curve fit with the Lassettre formula as presented in Fig.4. The extrapolated OOSs are compared with the previous available experimental and theoretical data in Fig.5. Note that the advantages and difficulties of various experimental methods to determine OOSs were commented by Chanet al.[34]The lower extrapolated data by Liet al.[35]can be rooted from their measured GOSs at 400 eV and 500 eV, where the higher Born terms might come in. The accordance between the present data with the dipole (e, e)[36,37]and dipole (γ,γ)[38]as well as the lifetime measurements[39,40]within the uncertainties confirms the reliability of the measured GOSs. The self-absorption[41–44]and pressure-broadening profile[45–48]methods are not the recommended experimental approaches for evaluating reliable OOS.Theoretical calculations with the relativistic many-body perturbation theory(RMBPT)[49]and BSR[50]method generated consistent data with the accurate experimental measurements while the recent RDW[32]calculation yielded a higher value for the 4s[3/2]1state and a lower value for the 4s′[1/2]1state.

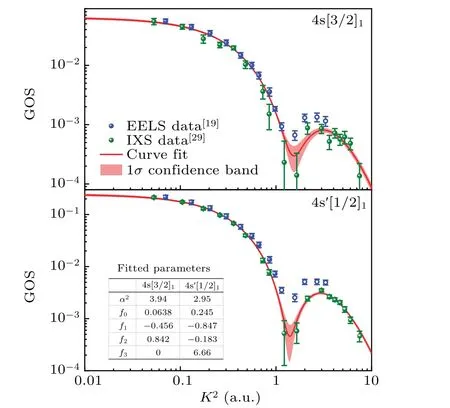
Fig. 4. GOSs of the 3p54s[3/2]1 and 3p54s′[1/2]1 states in Ar from the EELS[19] and IXS[29] measurements. The solid lines are the fitted curve by Lassettre formula and the shaded areas indicate the confidence band at 1σ level. It should be noted that the opened circles are the data points neglected during the fit since they are dominated by the higher-Born terms.

Electron impact excitations to the 4s[3/2]1and 4s′[1/2]1states have been extensively studied while the measured ICSs were only available at impact energies below 100 eV.The measured ICS data for the 4s[3/2]1and 4s′[1/2]1states before 2005 have been collected and discussed in Ref. [52]. Actually, the available data varied significantly while the absolute normalization usually carried large uncertainties which can make up for most of the divergences. With the aid of the BEscaling method,[12,13]the ICSs for the 4s[3/2]1and 4s′[1/2]1states are derived from the cross-checked GOSs as presented in Fig.6. It should be emphasized that the BE-scaling method cannot manifest the exchange scattering which is important at impact energies approaching the excitation threshold. It was noticed before that the scaled ICSs are applicable for the transitions dominated by the dipole-allowed components whereas the scaling law might underestimate the cross sections at low collision energies for the transitions dominated by dipole-forbidden components.[14,53]

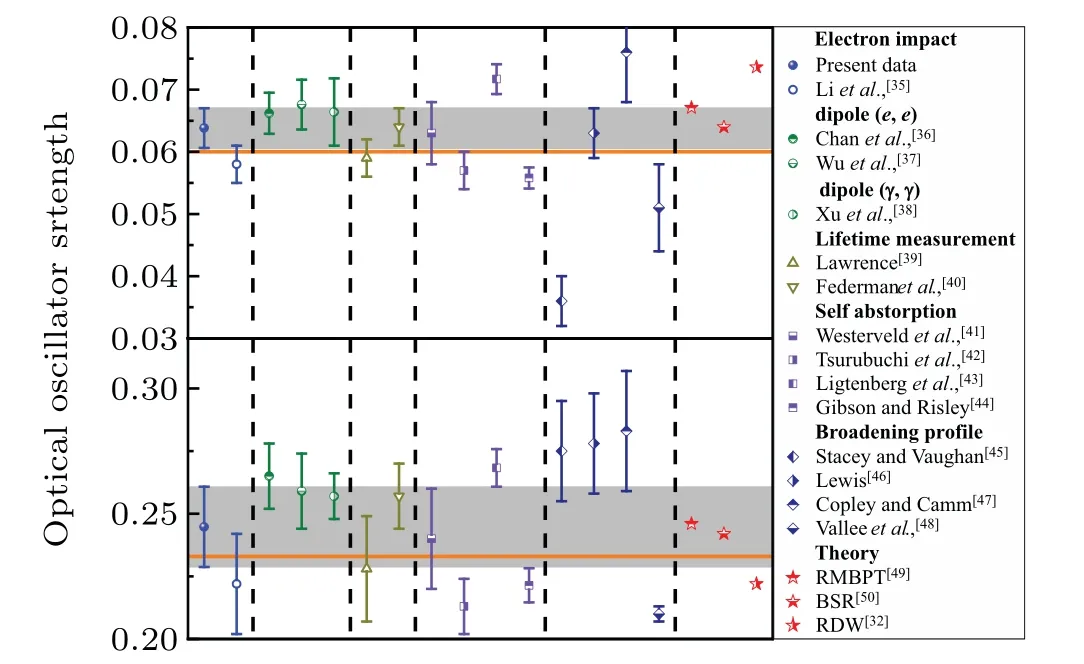
Fig.5. OOSs for the 3p54s[3/2]1 and 3p54s′[1/2]1 states of Ar in comparison with the available data from literature. The shaded areas correspond to the experimental uncertainties while the orange lines are previously recommended values.[51]

The measurements of Chutjian and Cartwright[54]agree with the present data for most cases while the cross section at 100 eV differs from the present line by more than 30%.The unexpected lower data might be caused by some systematic errors in their experiment. The measured data of Filipovicet al.[55,56]with impact energies of 20–50 eV differ quite a lot from the present data while the cross section at 80 eV lies within the present error bars. The larger data in their experiments can be rooted from their larger DCSs and the huge difference might be attributed to some unexpected systematic errors in the absolute normalization. The measured cross sections of Khakooet al.[57]were not accuracy enough due to the lack of data above 140?and the excitation and ionization coefficients from their ICS data were not consistent with the measurements.[52]Their data were adopted in the collection[52]by multiplying with a factor of 0.5 to yield consistent excitation coefficients with earlier experiments.The most recent measurement by Hoshinoet al.[58]was compared with the B-splineR-matrix(BSR)calculations in Ref. [59]. The data of Hoshinoet al.agree with the present scaled ICS for the 4s′[1/2]1state while the case for the 4s[3/2]1state is not satisfying. The reason might be that the dipole-allowed component dominates the wave function of the 4s′[1/2]1state while the spin-flip component dominates in the 4s[3/2]1state.[14,53]

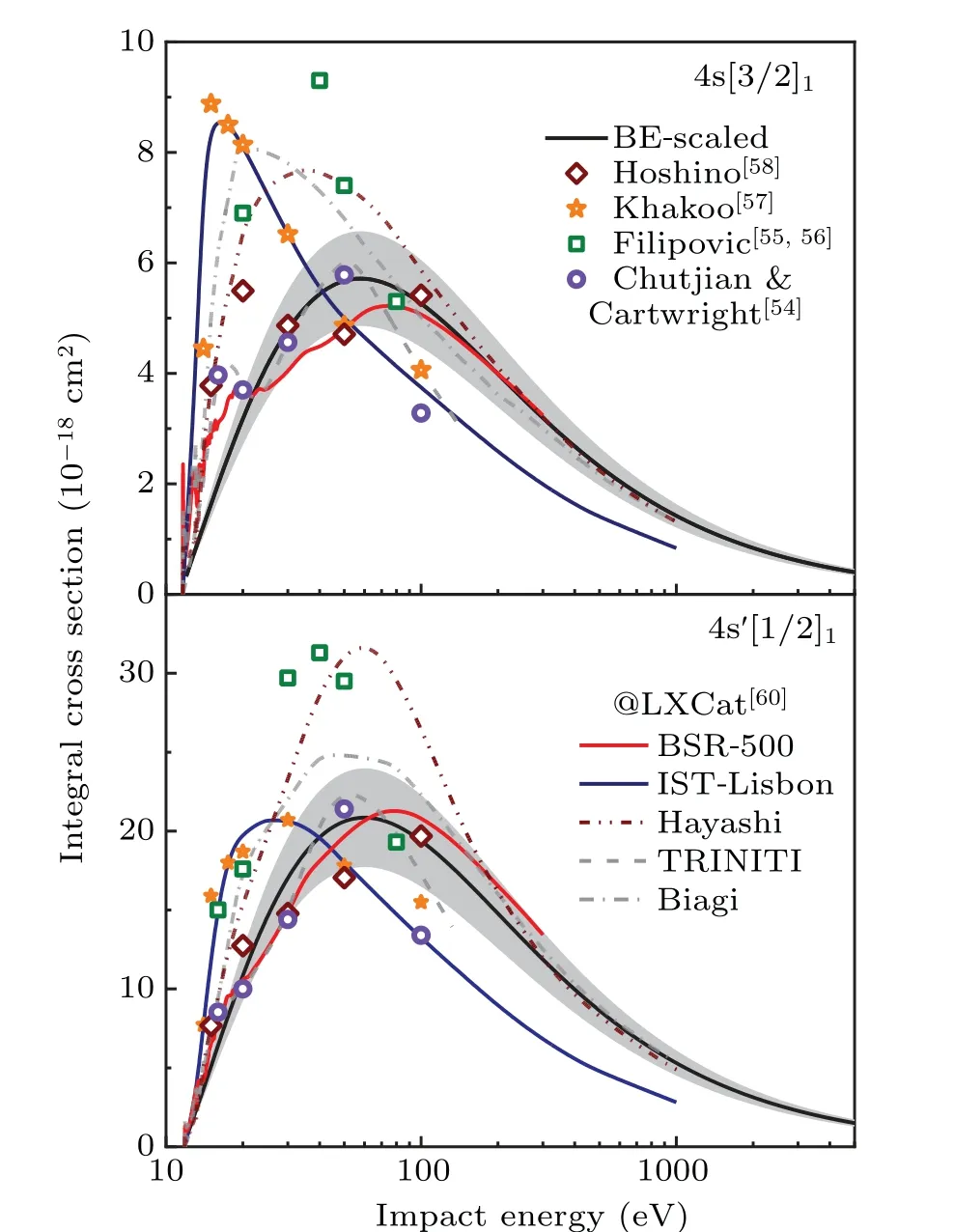
Fig.6. The BE-scaled ICSs for the 3p54s[3/2]1 and 3p54s′[1/2]1 states of Ar along with the previous available data. The shaded areas indicate an experimental uncertainty of 15%. The lines in the legend of lower panel are the data from the LXCat database.

For the convenience of plasma modelers, electron-argon scattering data sets have been collected and compared[60]in databases on the website LXCat. The data are found consistent with the present scaled ICSs at impact energies higher than 100 eV except for data of IST-Lisbon[52]which are generated from the inaccurate data of Khakooet al.[57]It should be noted that the exchange between the incident and target electrons dominates the cross sections at lower energies,i.e.,several times of the excitations energies. The BSR method[59]with an extended close-coupling expansion can yield accurate data from the excitation threshold to a few hundreds eV.The BE-scaled ICSs agree well with the most recent BSR-500 calculations except for the 3p54s[3/2]1resonances near the excitation threshold. This is reasonable because BE-scaling method cannot reproduce the resonance features at very low energies and the spin-flip component dominates the wavefunction of the 3p54s[3/2]1state. The major differences between the present data and previous measurements are also found at very low impact energies(below 30 eV).However, the RDW method can generate reliable data in most cases from intermediate energies (more than three times of the excitation energies)to higher.[60]Recent theoretical investigation[61]has also shown that the exchange effect as well as the polarization and absorption potentials are important for the low-energy electron scattering. These complicated potentials make the calculation of ICSs near the excitation threshold a challenge task.The BEscaled ICSs from the joint measurements by electron and x-ray scatterings can serve as a set of reliable data for applications.

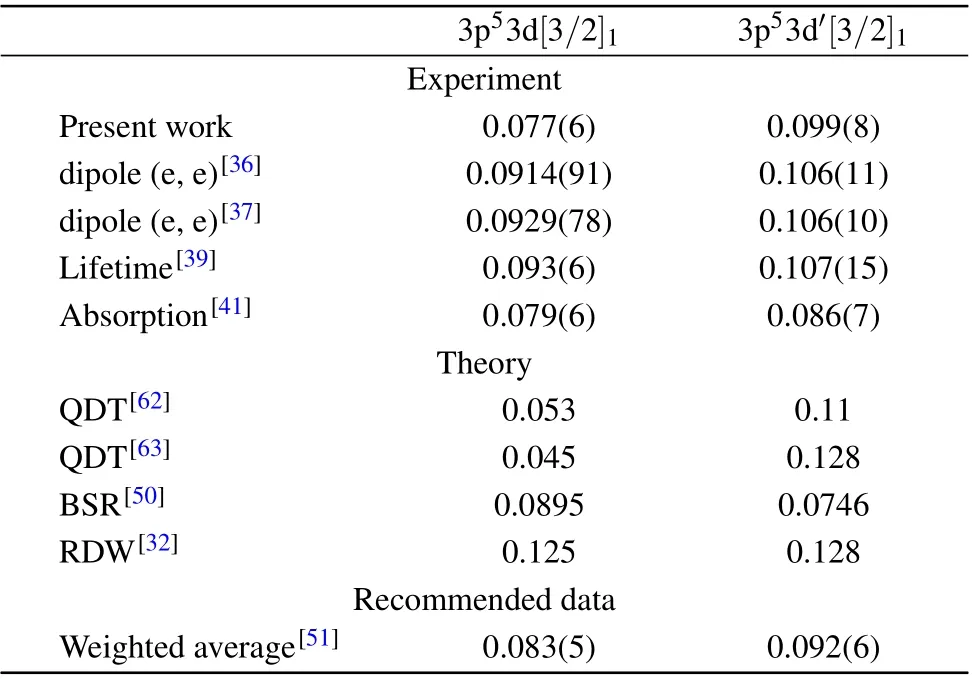
Table 1. Optical oscillator strengths (OOSs) of the 3p53d[3/2]1 and 3p53d′[3/2]1 states for argon.

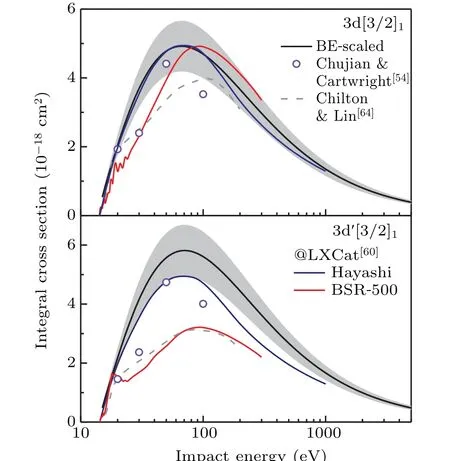
Fig.7. The BE-scaled ICSs for the 3p53d[3/2]1 and 3p53d′[3/2]1 states of Ar in comparison with the available data in literature and LXCat database. The shaded area indicates an experimental uncertainty of 15%.

The GOSs of 3p53d[3/2]1and 3p53d′[3/2]1states were reported in Ref. [19]. Theoretical calculation under the FBA shows only minor discrepancies with the RDW calculation.[32]The obtained OOSs are found in accordance with the latest recommended data originated from the weighted-average experimental data as listed in Table 1. The error bars can mostly make up for the difference between the extrapolations and dipole(e,e)measurements.[36,37]The data deduced from lifetime[39]and self-absorption[41]measurements are also found in agreement within 20%. Theoretical approaches including the quantum-defect theory (QDT),[62,63]BSR[50]and RDW[32]have been used to calculate the OOS.The earlier QDT calculations generated an accordant sum OOS while the distribution between two states was not accurate. The RDW calculations produced higher OOSs over the experimental data. The BE-scaled ICSs for 3p53d[3/2]1and 3p53d′[3/2]1states are compared with the available data[54,59,60,64]in Fig.7.The agreement between the scaled ICS and other data for the 3p53d[3/2]1state is good while the case for 3p53d′[3/2]1state is not satisfying. The stronger spin-flip components and the mixture with 4d components in the latter might be the primary cause of the difference.

3.2. Carbon dioxide

Carbon dioxide (CO2) is considered as a significant medium in global warming on planet Earth. The important role of excitations for CO2in the electron cooling mechanism in Mars and Venus was identified in early years by Morrison and Greene.[65]The energy loss rates are also required in understanding the electron energy transfer processes. The GOSs or ISFFs of the low-lying states have been extensively studied by electron[22,66–68]and x-ray[22]scattering for CO2. On the theoretical side, Buenkeret al.[69]first realized that the molecular bending resulted in intense features around 11 eV.The vibronic effects were overlooked until Watanabeet al.[68]evaluated a better agreement between experimental measurement and theoretical calculation within the vibronic effects.

The first feature in the EELS spectra of CO2around 9 eV was identified as transitions to the1Πg,1Σ?uand1?ustates.[68,70]The transitions are dipole-forbidden in the linear geometry but become allowed in the bending frame.[70]The GOSs for the sum of them were studied before with incident electron energies of 1500 eV[22]and 3000 eV,[68]respectively.However, the statistical counts in the x-ray scattering are extremely low for analysis. Since the two data sets from electron scattering are consistent within the error bars, they both are taken into account for curve fit. As presented in Fig. 8, the GOS profile characterizes somewhat dipole-forbidden natures as increasing with the momentum transfers to reach a maximum and then decreasing. Significant contributions due to the vibronic effects were found,in particular at small momentum transfers. The extrapolated OOS(0.0127±0.0010)for the1Πgand1?ustates is consistent with the dipole(e,e)measurement(0.01318)[71]but a bit higher than the calculated data(0.0106)of Watanabeet al.[68]The BE-scaled ICSs for this feature are also derived.Note that the dipole-forbidden components in the feature might make the BE-scaled ICS not accurate enough.

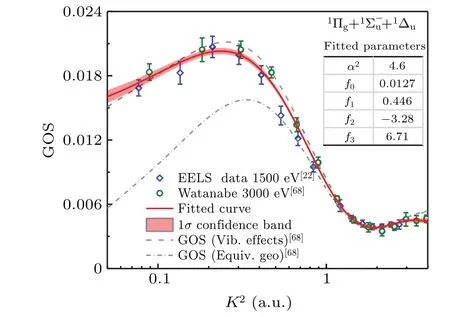
Fig. 8. GOSs of the 9 eV features of CO2 from EELS measurement.The electronic terms are inherited from previous literature.[68,70] The dashed-dotted and dashed lines are the theoretical calculations under the equilibrium geometry and within the vibronic effects.

The following two features are dipole-allowed transitions to the1Σ+uand1Πustates. Prominent contributions due to higher Born terms are found in the measured GOSs of the1Σ+ustate at large momentum transfers for the electron scattering.[22]The GOSs for the1Πustate by electron and xray scatterings show some minor difference at the same momentum transfers, i.e., the higher Born terms contribute only a little bit around the minimum. Anyway, the EELS data points around the minimum were skipped for the following curve fit. The extrapolated OOSs are compared with previous available data in Table 2. The extrapolations agree well with the accurate dipole (e, e) measurements[71]and the recent calculation with the coupled-cluster singles and doubles(CCSD)treatment.[68]Previous calculated data with the multireference single- and double-excitation configuration interaction (MRD-CI)[69]and separated-channel static-exchange(SCSE)[72]methods are much lower than the experimental results. The earlier calculation with the equation of motion(EOM)[73]method is also not accurate enough.

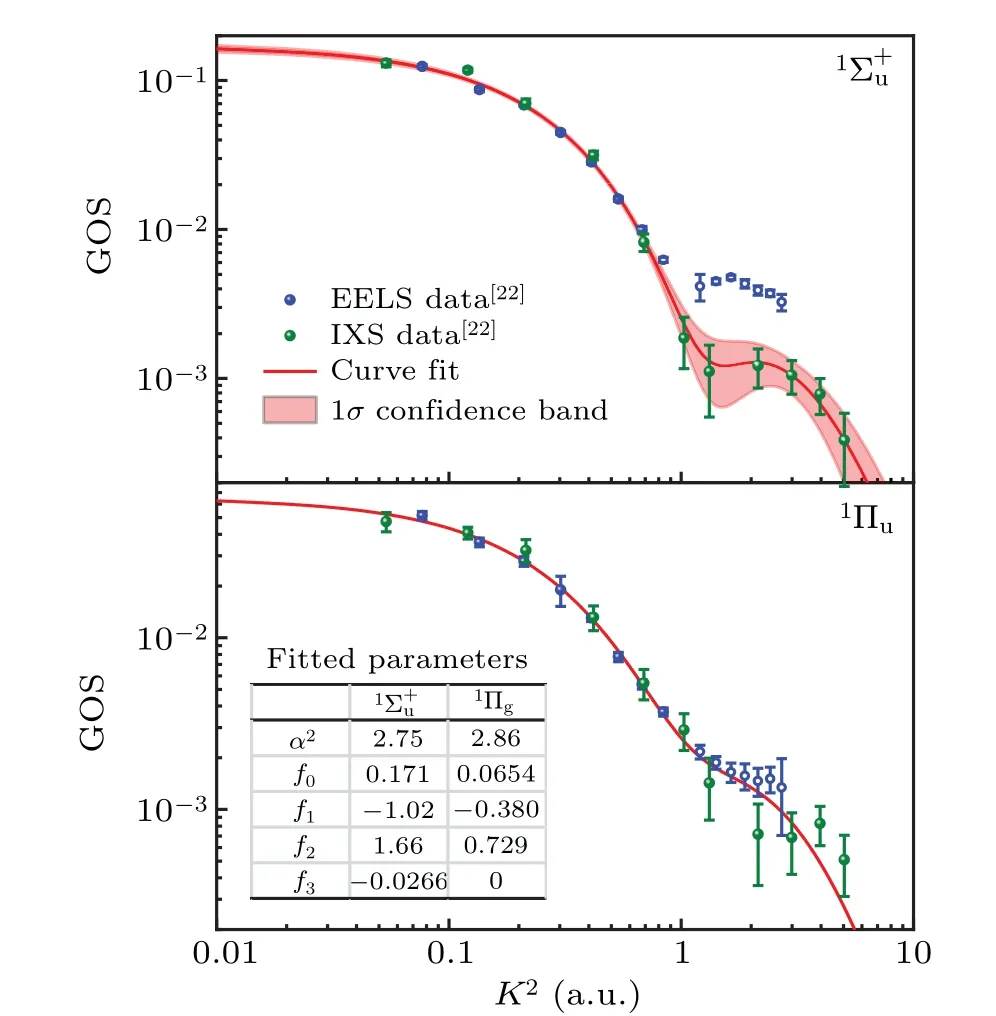
Fig.9. Same as Fig.4,but for GOSs of the 1Σ+u and 1Πu states of CO2.

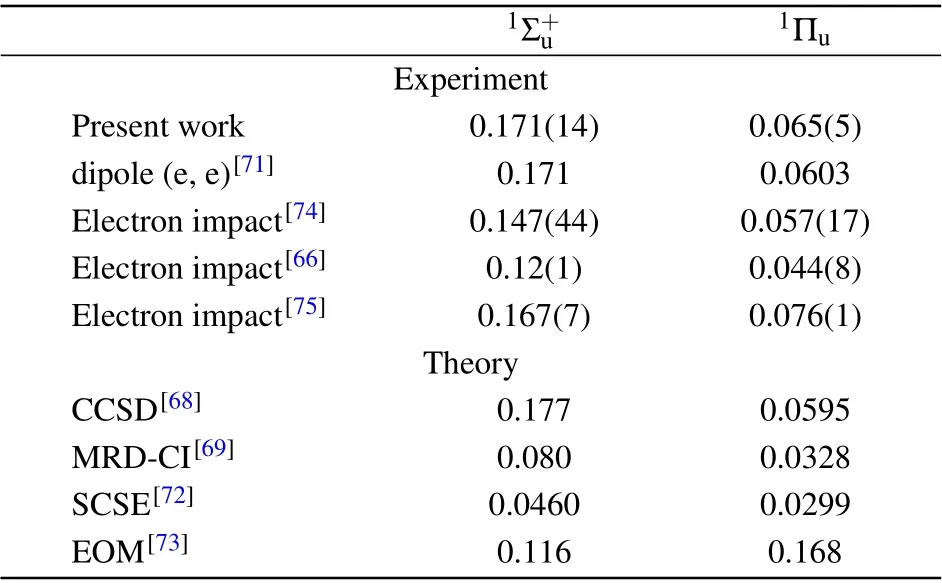
Table 2. Optical oscillator strengths for the low-lying states of CO2.

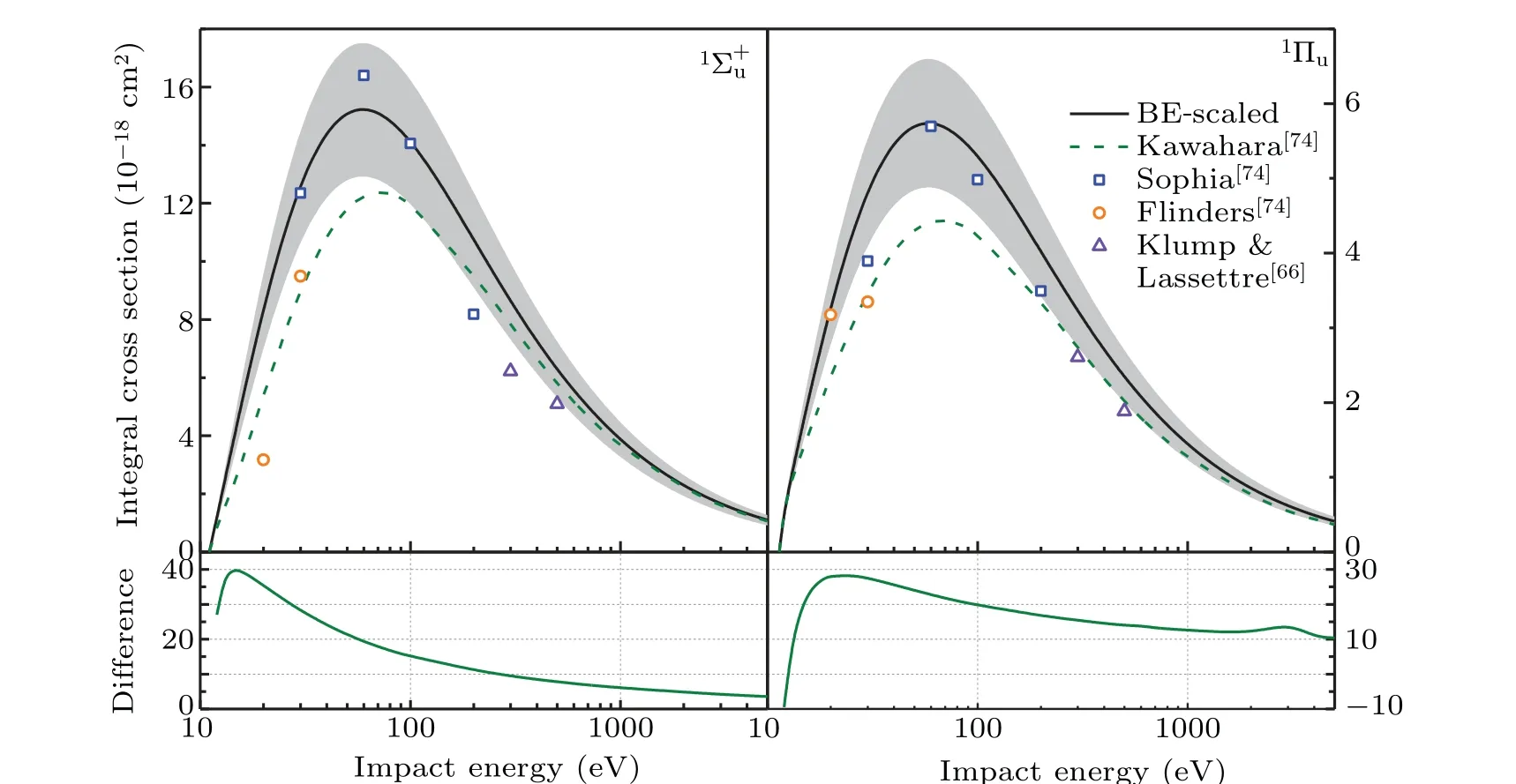
Fig. 10. BE-scaled ICS for the 1Σ+u and 1Πu states of CO2. The shaded areas indicate an uncertainty of 15%. The lower panels present the difference between the data of Kawahara et al.[74] and the present data.

The BE-scaled ICSs for the1Σ+uand1Πustates are plotted in Fig.10 along with the available data in literature. General agreement is found for the experimental measurements.The differences between the data of Kawaharaet al.[74]and the present scaled data for the1Σ+ustate are larger than 20%for impact energies below 50 eV while the differences are less than 10% for impact energies higher than 250 eV. As for the1Πustate,the differences are higher than 20%for impact energies below 100 eV.The lower BE-scaled ICSs of Kawaharaet al.[74]might be rooted from their DCS data measured at electron energies below 200 eV, where higher Born terms might make a significant contribution. The data from independent measurements at Sophia University and Flinders University were compiled in Ref.[67]and the corresponding ICSs were derived in Ref. [74]. The measured ICSs are generally consistent with the present data within error bars. The electron impact experiment of Klump and Lassettre[66]yielded a much lower OOSs than dipole(e,e)measurement and their ICS data are lower than the present scaled data as expected.

3.3. ICS data

To facilitate the modelers,the derived BE-scaled ICS data for Ar and CO2are listed in Table 3. The experimental uncertainties on the measured GOSs are estimated to be less than 10%.The uncertainties for the scaled ICSs should also include the uncertainties from the extrapolations via Lassettre formula and from the BE-scaling model. All the ICS data in this paper have also been compiled in the supplementary materials(SM)in PDF format.

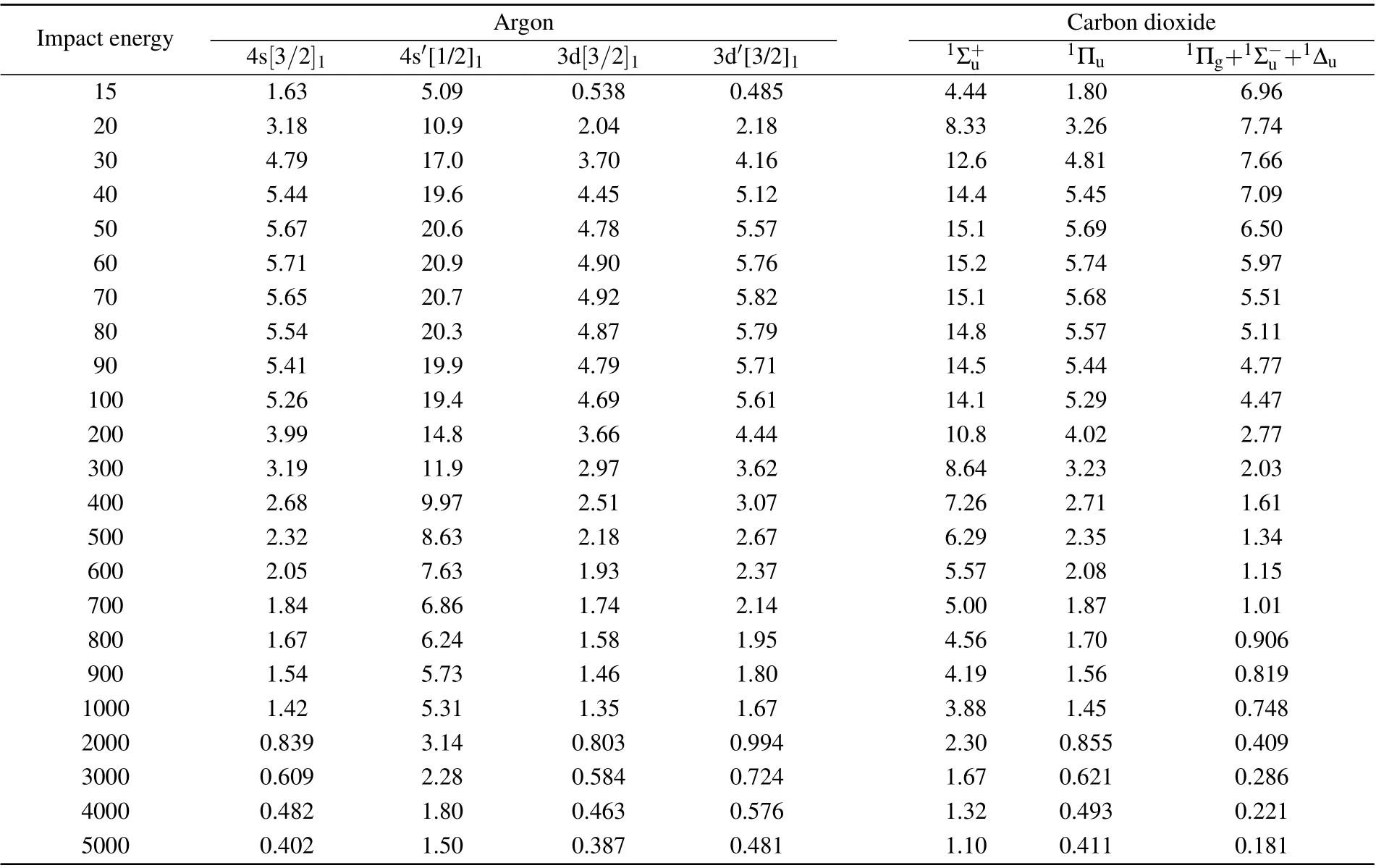
Table 3. The electron impact integral cross sections(ICSs)for the low-lying states of Ar and CO2. The units of the impact energies and cross sections are eV and 10?18 cm2,respectively.

4. Concluding remark

Summary The demand of atomic and molecular data should be comprehensive, correct and absolute, i.e, accurate ICS data over an extended impact energy range are required with an absolute scale. Here we present the joint measurements by fast electron and x-ray scattering of the GOSs for atomic argon and molecular carbon dioxide. The BE-scaled ICS data from the excitation threshold to 5000 eV are derived based on the reliable GOSs from comparative studies. The cross-checks from extensive perspectives can eliminate possible systematic errors and thus provide correct data. The absolute normalization was realized by adopting the relative flow technique. Generally, joint studies on the oscillator strengths and cross sections generate reliable experimental benchmarks not only for filling up the data table as a supplement but also for testing the theoretical models or computational codes. The fully validated atomic and molecular codes can further be used to produce reliable database for applications in applied sciences. Based on the cross-checked GOSs and the BE-scaling method,we have derived the new ICS data for some low-lying states of Ar and CO2from the excitation threshold to 5000 eV.The BE-scaled ICSs are compared with the available data in literature and LXCat database. We have also found that the BE-scaled ICSs may not accurate enough for those transitions with prominent dipole-forbidden components in atomic target.

Outlook The core of experimental measurements can be summarized in short as the supplement and benchmark. The experimentalists are aiming at reducing the uncertainties and developing new techniques for cross-checks. The demand of comprehensive,correct and absolute data could be met under the collaborations between experimentalists and theorists in all aspects. Currently,the valence-shell excitations of atoms and molecules have been extensively studied in the past decades while the data for inner-shell excitations are scarce due to their low cross sections. With the development of 2D analyzers and position-sensitive detectors, the collection efficiency will be improved prominently and the inner-shell studies will be possible. In addition,BE-scaling method enables one to produce reliable ICS data for dipole-allowed transitions of atoms and molecules. There are no efficient methods to generate reliable database for the dipole-forbidden transitions.

Data availability

The data that support the findings of this study are openly available in Science Data Bank at http://doi.org/10.11922/sciencedb.01466.

Acknowledgments

We acknowledge all the colleagues who have contributed his or her effort during the past few years on the development and improvement of fast electron and x-ray scattering experiments.

Project supported by the National Key Research and Development Program of China(Grant No.2017YFA0402300),the National Natural Science Foundation of China (Grant Nos.U1932207 and 12104437),and the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB34000000). The financial support from the Heavy Ion Research Facility in Lanzhou (HIRFL) is also acknowledged.