Lei Tao(陶蕾) and Sheng-Jun Wang(王圣軍)

School of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China

Keywords: power-law,inhibitory,synchronization,neuronal networks

1. Introduction

When the probability of measuring a particular value of some parameter varies inversely as a power of that value, the parameter is said to obey a power law.[1,2]Power-law statistics are ubiquitous in physics and life sciences[3–7]and occur in an extraordinarily diverse range of phenomena, from earthquakes[8–10]to forest fires,[11]the numbers of species in biological taxa,[12]the number of citations received by papers,[13]the number of hits on web pages.[14]These distributions reveal unusual properties:The observed parameter has no typical scale,for instance,size,duration,and shape of collective phenomena.[15–19]These singular properties,combined with their ubiquity in nature, have attracted wide attention in applied sciences.[1,3,20,21]

In neural systems, experiments have shown that avalanche sizes and durations obey a power law distribution.[22–28]There are several potential mechanisms behind the power-law distribution in the neural network.[1,20,21,29,30]In experimental studies on spontaneous local field potentials in mature organotypic cultures and acute slices of rat cortex,[20,23–28]it was shown that the mode of activity has a power-law distribution in neuronal avalanche sizes, and the power exponent coincides with that of a critical branching process.[31–33]The critical point of branching process means that the expected number of offspring per activated node is unity when activity propagates in the network.The critical branching process exhibits the power law distribution of avalanches,[34]and provides an explanation for the macroscopic statistics of the neural network.[20,31]

The avalanche can be identified in thresholding continuous times series.[21]In the random walk process,the avalanche duration is the amount of time that the walker exceeds above a given threshold,and the avalanche size is the area covered between the walk trajectory and the threshold reference line.It is shown that the avalanches have power-law-distributed size and duration.[21]The underlying dynamics of the power-law statistics is the fluctuation around a given mean value, rather than the propagation of activity described by the branching process.

Synchronization is another important phenomenon in neural networks.[32,35–40]The emergence of a unified cognition relies on the coordination of scattered mosaics of functionally specialized brain regions.[41]However, anomalous synchrony among neurons is related to neurological disorders.[42,43]The intermediate levels of synchrony play an important role in neuronal activity.[44,45]It was shown that moderate and variable levels of synchrony and critical neuronal avalanches occur in networks operating near a balanced condition between excitatory and inhibitory neurons.[46]In neural networks composed of the local excitatory and inhibitory populations,the putative criticality of cortical dynamics corresponds to a synchronization phase transition,at which incipient oscillations and scale-free avalanches coexist.[45]It was suggested that criticality in excitatory networks is established by regulation of inhibition.[47]

Recently,the transition from asynchronous to oscillatory dynamics has been found in balanced spiking networks in which the balance occurs between the external dc current and pulse-coupled inhibitory neurons.[48]In balanced networks,collective oscillations can be triggered by microscopic irregular fluctuations.[48]Different from networks consisting of excitatory and inhibitory neurons,activity does not propagate in the networks of coupled inhibitory neurons. This dynamical model raises interesting questions. Without excitatory neurons which propagate activity,does the fluctuation exhibit the power law statistics? What is the relationship between transition and power-law behavior at a macroscopic level?

In the present work, we use the inhibitory spiking networks to study the relationship between the neuronal activity at the transition point from asynchronous to oscillatory and power-law statistics. We show that the event size and duration in the macroscopic dynamics obey a power-law distribution in the transition from asynchronous to oscillatory dynamics. The distribution exponent of the event size and duration distribution satisfies the critical scaling relation.

2. Model

We adopt the spiking network obeying the quadraticintegrate and fire(QIF)model proposed in Ref.[48]. The network consists ofN=10000 pulse-coupled inhibitory neurons whose membrane potentialvievolves as

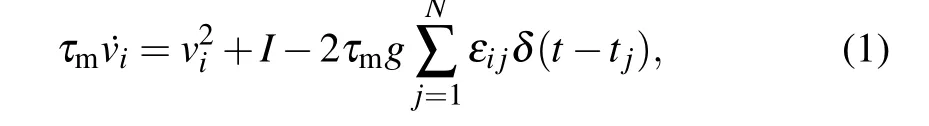
3. Result

In the spiking neural network, we perform a parameter search by varying the average degreeKand heterogeneity parameters?0to find the power-law distribution of events. Frequently, complex dynamical systems like the brain cannot be sampled completely.[50]Similar to the measurement of network activity in experiments,[20,46,51]we implement subsampling in the model. Here we calculate the event size and duration distribution of the 1000 neurons in the time window of 109ms.

3.1. Event size distribution

Following the approach taken in experimental investigations,we divide the time series into short time bins,which has a width of ?t ～1–20 ms.The event is defined as a sequence of consecutively active between two empty adjacent bins in neuronal activity.[20,44,52]Event sizesis measured by the number of exciting neurons in the event. Event lifetimetlis measured by the number of time bins an event spans. Event waiting timetsis measured by the number of time bins that the resting state spans.

In the spiking network, it is straightforward to see that changes in the average degreeKand the structure heterogeneity parameter?0can bring the transition of synchronous dynamics [as shown in the insets of Figs. 1(a) and 1(b)].[48]In the parameter region of the transition from asynchronous to synchronous dynamics, we calculate the event size distribution. Figure 1 shows the event size distribution of the neuronal network. AtK=600 (Fig. 1(a), circles), the event size distribution obeys a power lawP(n)～n?τswith a cutoff. We estimate the distribution exponentτsusing the least square fitting. In the fitting we ignore the cutoff, i.e.,s>35. The power law distribution has exponentτs≈2.05. At?0=0.13(Fig.1(b), circles), the event size distribution obeys the same power law and has the same exponent.By increasing the number of subsampling neurons,the distribution of the event size still exhibits the power-law distribution, but the exponent of events size distribution is smaller. We only present the results obtained using the subsampling of 1000 neurons.

The event size distribution depends on the average degreeK(Fig. 1). In Fig. 1(a) triangles and squares show the event size distribution of networks with larger and smaller average degrees,respectively. ForK=300,the neuronal network is in a desynchronized state. The decrease ofKleads to an increase in the number of small events, and results in the exponential distribution of event sizes. ForK=2500, the neuronal network is in a highly synchronous state. Thus many neurons are excited at the same time bin, the number of large events increases and non-monotonic characteristic appears at the end of the distribution. Therefore, when neuronal network is in both desynchronized and synchronized states, the event size does not obey a power law distribution.

In Fig.1(b),triangles and squares show the event size distribution for different structure heterogeneity parameter?0.As structure heterogeneity parameter?0increases, the network synchronization decreases (Fig. 1(b), inset). For?0=0.03, the neuronal network is in a synchronous state. The change of?0leads to an increase in the network activity,and results in an increase in the number of large events. The event size distribution has a characteristic hump at the end of the loglog coordinates. For?0=0.22, the neuronal network is in a desynchronized state. The increase of?0leads to an decrease in the network activity. The event size distribution decays exponentially. Therefore,the power law distribution only exists in the parameter regime of the transition from asynchronous to synchronous dynamics.

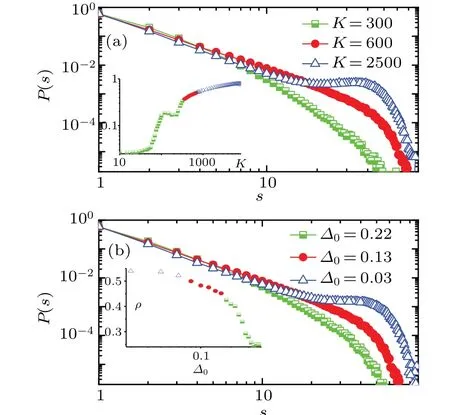
Fig.1. Distributions of event size S. (a)The average degree K is 300,600,and 2500,respectively. (b)The structure heterogeneity parameter?0 is 0.22, 0.13, and 0.03, respectively. Inset: the order parameter ρ changes with the network parameter. (a) (?0, g0, I0, ?t)=(0.13, 1.0,0.006,10). (b)(K,g0,I0,?t)=(600,1.0,0.006,10).

In the network the dissipative role of inhibition hinders the occurrence of large events.[54]Although we have selected 1000 neurons to measure the event size distribution,the maximum size of the event is still less than 100.The maximum size and cut-off point of the events are much smaller than the number of neurons. Furthermore, the cutoff of the distribution in the model is not as sharp as experimental results in Ref.[20],where the finite size of sampling is the only mechanism for the cutoff.

The distribution exponent and cut-off point of the event size distribution of the inhibitory neuronal network are different from the experimental results obtained in Ref.[20]. In the experiment,[20]the event size distribution obeys a power law distribution with exponent?1.5. Moreover,experiments have shown that the maximum size of the event is approximately equal to the number of electrodes in the array. Compared with the experimental results,[20]our exponent of the event size distribution is larger, and the maximum size of the event decreases. Our distribution tends toward more small events and fewer large events.

For more stringent statistical analyses,[53]we estimate the exponent of distribution for the finite range of sizes by the three methods, least-square (LS), Kolmogorov–Smirnov(KS),and maximum likelihood(ML).In the transition of synchronous dynamics,the exponent parameter of events size distributionτsestimated are close to 2.05 by using three methods (Fig. 2(a)). The KS distance of the model distributions isD=0.004. In addition, we compare the power law model of event sizes distribution with the exponential, log-normal,gamma, and inverse Gaussian model distribution. We assess goodness of fit using the KS distance (Fig. 2(b)) and loglikelihood ratio (LLR) (Fig. 2(c)). The KS distance of the power law model is the smallest,that is,the power law model yields a better fit for the event size distributions. The LLR is the difference between the log-likelihood of power law and the alternative model.[53]The LLRs for the power law and the other distributions are larger than zero,that is,the power law is considered to be the better model for event distribution when compared to the other distributions. These results indicate that the power law provides a good description of the size distribution in neuronal avalanches.

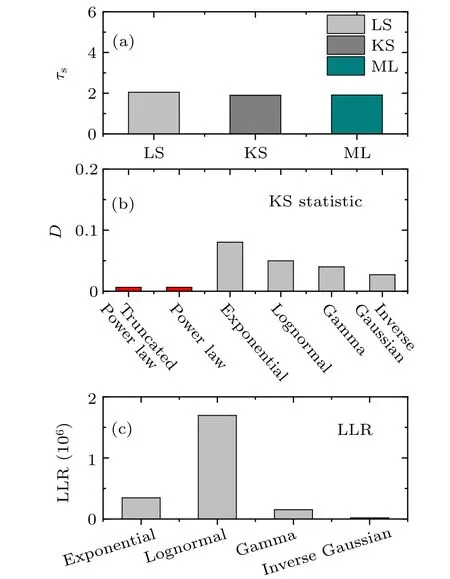
Fig. 2. Model comparison using the Kolmogorov–Smirnov (KS) distance and the log-likelihood ratio (LLR) test for the size distribution(K =600) shown in Fig. 1(a). (a) Estimation of distribution exponent τs using three methods. (b)The KS distance D of the event size distribution from power law function and other functions. (c) Model comparison using the log-likelihood ratio(LLR)test for the power law.

Figure 3 shows the event size distribution exponents of the neuronal activity in the transition of synchronous dynamics.For different parameters,the KS distance is less than 0.02.For simplicity, we use only least square fitting in the following results. As the average degreeKincreases (Fig. 3(a)),the exponentτsof the event size distribution decreases. The change of exponent can be intuitively interpreted. As the network connection becomes dense, and the synchronization of the network is enhanced, and the probability of large events increases. Conversely,increasing the heterogeneity parameter?0,the distribution exponentτsincreases(Fig.3(b)),because the synchronization of the network is weakened. In the transition of synchronous dynamics, the distribution exponentτsexhibits a clear dependence on network parameters.

Fig. 3. The exponent of the event size distribution as a function of the network parameters. (a) The distribution exponent increases with the average degree K. (b)The distribution exponent increases with the structure heterogeneity parameter ?0. The parameters are taken as (a)(K, ?0, g0, I0, ?t)=(400–1200, 0.13, 1.00, 0.006, 10) and (b) (K, ?0,g0,I0,?t)=(600,0.07–0.17,1.00,0.006,10).

3.2. Robustness of power law

Empirical data from experiments showed the robustness of the power law statistics.[20,24,26,27]Here, we consider the robustness of the power law in the spiking networks at multiple time scales. For different time bins,the KS distance is less than 0.02.

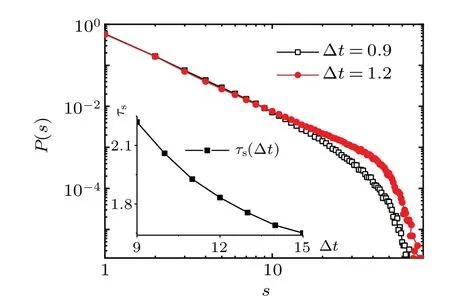
Fig.4. The event size distribution obeys a power law at multiple time scales. Inset: the exponent of the event waiting time distribution τs as a function of the time bin width ?t. The width of the time bin ?t increases,leading to the exponent of the event size distribution decreasing. The parameters are taken as(K, ?0, g0, I0, ?t)=(600, 0.13, 1.00,0.006,10).

Figure 4 shows the power law distribution of the event size in different time bins. The exponentτsof the event size distribution obviously depends on the width of time bin ?t.By increasing ?t,many neurons will be grouped into the same bin. Several smaller events concatenate together into a longer event. Thus, the exponent of the event size distribution decreases (Fig. 4, inset). Conversely, the decrease of the time bin width leads to an increase in the number of smaller events,and then results in an increase in the exponent of the event size distribution. Consistent with the experimental results,[20]we demonstrate the robustness of the power law in the network model at multiple time scales.

3.3. Event duration distribution

The exponent of event lifetime distribution has been shown to be an important parameter that characterizes the temporal properties of systems dynamics.In the spiking networks,the event lifetime(Fig.5(a))and waiting time(Fig.5(b))obey a power law distribution in the region of transition from asynchronous to synchronous dynamics. In Fig.5(a),fortl<1.5,the characteristic exponentτTof event lifetime distribution by the three methods is 2.29,D=0.003. In Fig.5(b),forts<3.4,the characteristic exponent of event waiting time distribution by the three methods is 1.45,D=0.007.By the increase in the number of subsampling neurons, the distribution of the event size still exhibits a power-law distribution,but the exponent of event lifetime distribution is smaller. The event lifetimes tend toward more large events and less small events.

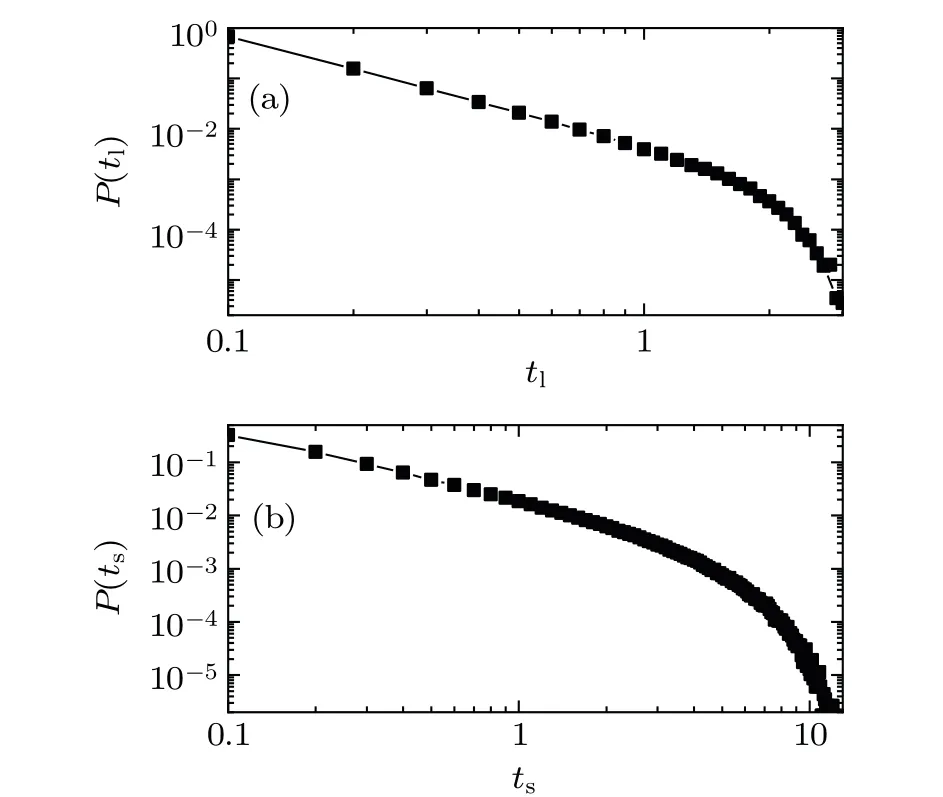
Fig.5. (a)Event lifetimes distribution. (b)Event waiting times distribution. For the region of the transition of synchronous dynamics, the event lifetime and waiting time obey a power law distribution. Take the parameters as(K,?0,g0,I0,?t)=(600,0.13,1.00,0.006,10).

In the literature on the neuronal avalanches of cortex cultures,[20]the avalanche duration obeys power law distribution, and the characteristic exponent of the avalanche lifetime distribution is 2. Compared to the power law distribution of the avalanche lifetime in experiment,[20]our characteristic exponent of the event lifetime distribution is larger. In the inhibitory neuron network, the event lifetime distribution shows that large events occur less frequently,while small-scale events occur more frequently.

3.4. Scaling relation of criticality

Scaling relation is used as a stronger criterion to test the authenticity of the critical point.[3]The scaling relation is based on the result that at criticality the average event size〈s〉for a given durationTmust obey

whereτTis the exponent of the event lifetime distribution,andτsis the exponent of the event size distribution.Equation(4)is a stronger criterion for criticality because it would not be satisfied by non-critical models.[3]The scaling relation has been supported by several investigations.[44,51,55]In some experimental investigations and theoretical models, the critical exponents are(τT?1)/(τs?1)=1.28±0.02.[44,51]

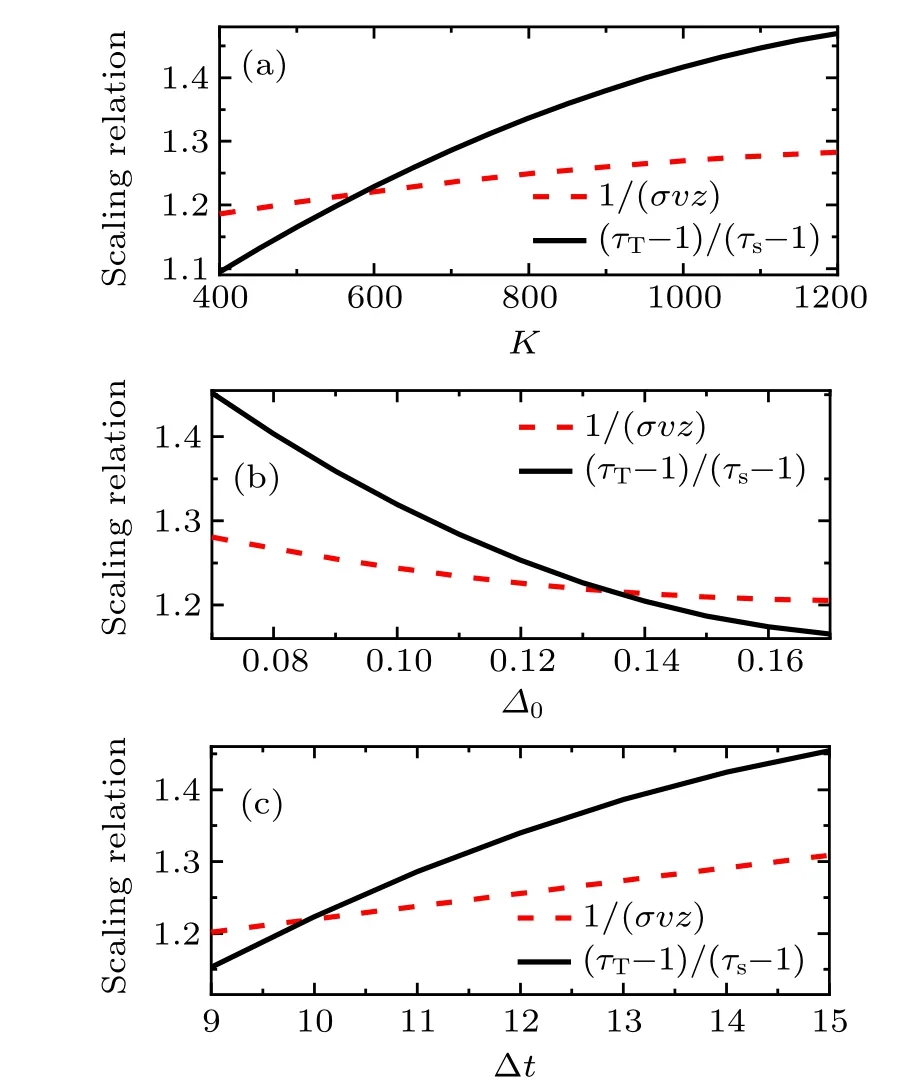
Fig.6. Scaling relation plot of the exponent of the event size and duration distribution for different parameters.Right-and left-sides of Eq.(4)as a function of the average degree K,for the structure heterogeneity parameter ?0, and the time bins ?t in (a), (b) and (c), respectively. The parameters are taken as(a)(K,?0,g0,I0,?t)=(400–1200,0.13,1.00,0.006, 10). (b) (K, ?0, g0, I0, ?t)=(600, 0.07–0.17, 1.00, 0.006, 10).(c)(K,?0,g0,I0,?t)=(600,0.13,1.00,0.006,9–15).

We calculate the distribution exponent for different parameters, then find the parameters which satisfy the scaling relation (4). Figure 6 shows the left- and right-hand sides of Eq. (4) as a function of the network structure parameter or the time bin. On the intersection of (τT?1)/(τs?1) and 1/(σνz),the scaling relation(4)is satisfied. The intersection of the distribution exponent appears at parameters ofK=600 in Fig.6(a),?0=0.13 in Fig.6(b), and ?t=10 in Fig.6(c).On the intersection point in Fig.5,distribution exponents areτT=2.29,τs=2.05,and 1/(σνz)≈1.22. The values of network structure parameters are the same as those of the transition from asynchronous to oscillatory dynamics.

Furthermore,when critical exponents are estimated from data,they widely differ across species,individuals of the same species.[22–27]In theoretical studies, quasicriticality predicts that increased drive will force cortical networks to depart from criticality, while still holding approximately to a dynamical scaling relation.[54]

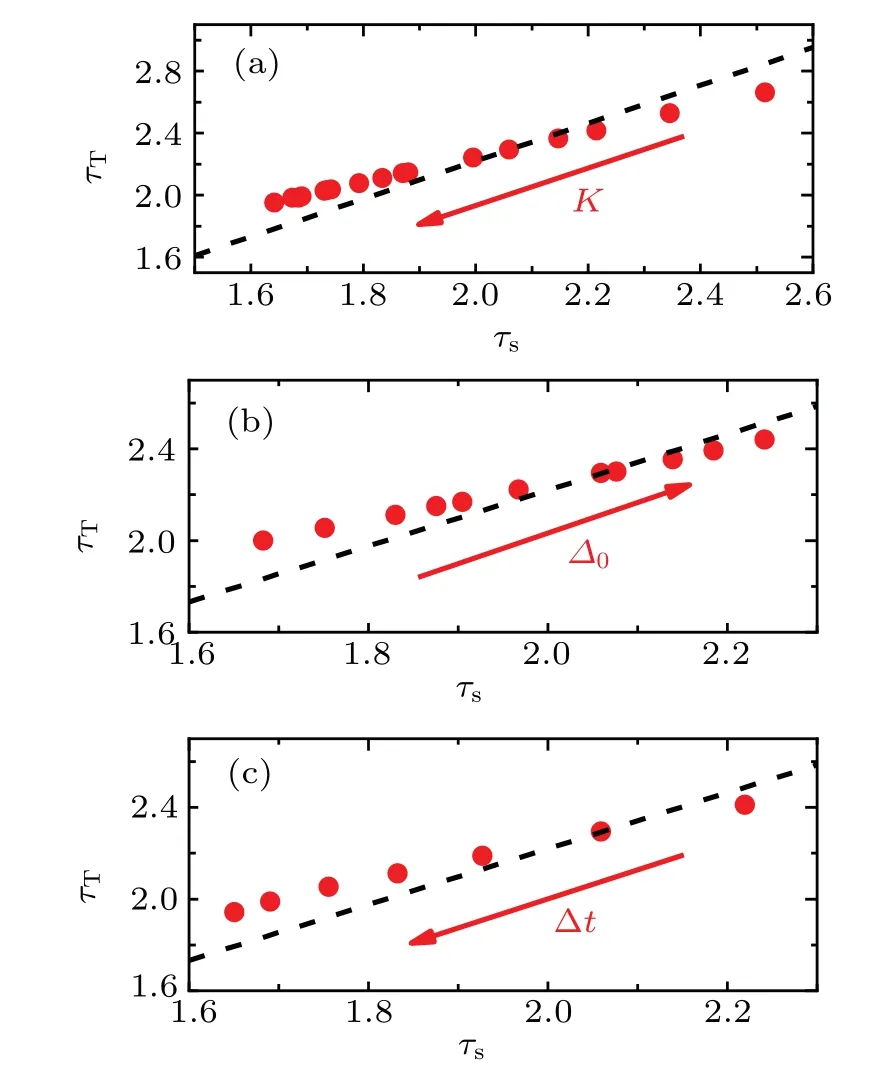
Fig.7. Exponent relations and critical scaling line of different network structure parameters and time bin parameters. [(a),(c)]As the average degree K and the time bin ?t are increased(red arrow),the distribution exponent(red circles)decreases, while still holds to the power-law relation for K ∈[400,1200],?t ∈[9,15],respectively. (b)The increase of structure heterogeneity parameter ?0 (red arrow) leads to the increase of the distribution exponent(red circles)for ?0 ∈[0.07,0.17].The slope of the dashed line is 1.22,which satisfies the relation(4). Take the parameters as (a) (K, ?0, g0, I0, ?t)=(400–1200, 0.13, 1.00, 0.006, 10),(b)(K,?0,g0,I0,?t)=(600,0.07-0.17,1.00,0.006,10),(c)(K,?0,g0,I0,?t)=(600,0.13,1.00,0.006,9–15).

In the inhibitory neuron network, the exponents change for different network structure and time bin,as shown in Fig.3.Here,in order to investigate the quasicriticality,we plotτsvs.τTfor the inhibitory neuron network in Fig. 7. The distribution exponent scatters along the dashed line with a slope 1.22 for different parameters. Obviously, asKincreases or?0decreases, the network synchronization increases, the distribution exponent decreases. Similarly,the widths of the time bin also drive the distribution exponent change. The increase in the time bin width leads to an increase in the exponent of the event size distribution. Although the distribution exponent is different for different parameters,these exponents still hold to a dynamical scaling relation. The behavior is consistent with the prediction of quasicriticality.

4. Conclusion

In summary, we have studied the event size of the neuronal activity and its relation to the synchrony transition in the spiking networks composed of inhibitory neurons and driven by external dc current. Using stringent statistical analyses,we show that,in the parameter region of the transition from asynchronous to oscillatory dynamics, event size distribution has a power law distribution with a cutoff smaller than the system size. The power law distribution is robust against the time scale parameters. The behavior is the same as experimental observations that power law distribution of avalanche sizes exists and is robust in cortical networks.[20]The power law distribution is also robust against the network structure parameters in the region of transition. Importantly,the distribution exponents of event size and lifetime can satisfy the critical scaling relation in the region of transition of synchrony. Recently, it has been shown that quasicritical states allow the exponents produced under varying conditions to depart from the criticality while still hold approximately to a dynamical scaling relation.[55]In coupled inhibitory neuronal networks, as the distribution exponents are changed by network structure and time scale parameters, these distribution exponents still hold to a dynamical scaling relation in the parameter region of synchrony transition. In coupled inhibitory neuronal networks,for different parameters,the distribution exponent fulfills quasicriticality’s specific predictions.

Our results are different from the previous work on the relation between synchronization transition and critical avalanche, in which excitatory and inhibitory elements were coupled together.[45]Here,inhibitory signal is balanced by the external dc current. The activity does not propagate in the network. Our results suggest that excitatory coupling and activity propagation are not necessary condition for the power law statistics in the edge of synchrony. The activity of the model provides a mechanism of collective behavior that exhibits the statistics of critical neuronal avalanche,but the exponents are different. This result could provide the new insights on the understanding of the power-law statistics of complex network systems.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant No. 11675096) and the Fund for the Academic Leaders and Academic Backbones, Shaanxi Normal University,China(Grant No.16QNGG007).