Fazal Haq Muhammad Ijaz Khan Sami Ullah Khan Khadijah M Abualnaja and M A El-Shorbagy

1Department of Mathematics,Karakoram International University Main Campus,Gilgit 15100,Pakistan

2Department of Mathematics and Statistics,Riphah International University I-14,Islamabad 44000,Pakistan

3Department of Mechanics and Engineering Science,Peking University,Beijing 100871,China

4Department of Mathematics,COMSATS University Islamabad,Sahiwal 57000,Pakistan

5Department of Mathematics and Statistics,College of Science,Taif University,P.O.Box 11099,Taif 21944,Saudi Arabia

6Department of Mathematics,College of Science and Humanities in Al-Kharj,Prince Sattam bin Abdulaziz University,Al-Kharj 11942,Saudi Arabia

7Department of Basic Engineering Science,Faculty of Engineering,Menoufia University,Shebin El-Kom 32511,Egypt

Keywords: Jeffrey nonmaterial, entropy generation, magnetohydrodynamics (MHD), Bejan number, porous medium,Brownian motion

1. Introduction

Rheological behavior of fluids,frequently used in industries differs remarkedly from Newtonian fluids. Such fluids are known as non-Newtonian fluids and have extensive utilizations in various fields of engineering and science, such as plastics manufacturing, food processing, wire coating, dying of papers,and glass fibers production,etc. The Jeffrey model is one of the most important models of non-Newtonian fluids.The Jeffery fluid model was initially introduced by scientist Jeffery[1]to study the characteristics of viscous fluids. Recently the Jeffrey model has attracted much research because of its applications in many natural areas and industry. Hayatet al.[2]reported the three-dimensional(3D)flow behavior of Jeffrey fluid due to nonlinear stretched sheet. Heat and mass transportation in flow of Jeffrey liquid in existence of heat source due to stretched surface is reported by Qasim.[3]Reddyet al.[4]investigated flow features of Jeffrey liquid among to torsionally fluctuating disks. Magnetic field on the Jeffrey fluid flow in tubes,having small diameter is reported by Nallapu and Radhakrishnamacharya.[5]For recent developments in Jeffrey fluid interested readers may consult in Refs.[6–11]

A colloidal suspension of nanoparticles (1 nm–100 nm)into base fluids such as water, Ethylene, bio-fluids, oil, and other lubricants,etc. is a nanofluid or nanomaterial. Oxide particles, metallic particles, carbon nanotubes, and ceramic particles are commonly used in the formation of nanomaterials. Having higher thermal conductivity and heat transfer rate, nanomaterials have attracted the interest of researchers in the last decade. Hwanget al.[12]investigated nanofluids to study their lubrication features and thermal conductivity.Experimental and theoretical investigations were conducted to explore the thermal conductivity and viscosity of nanomaterial flow by Murshedet al.[13]Hayatet al.[14]inspected the flow features of a Ree–Eyring nanoliquid with a heat source,activation energy, and viscous dissipation between two rotating disks. Khanet al.[15]addressed stagnation point flow in cross nanoliquid considering mixed convection, magnetohydrodynamics(MHD),radiation,and activation energy effects.Recent advancements in nanofluids are listed in Refs.[16–23].

The study of fluid flows over a porous-medium surface has gained much attention due to its versatile usages in engineering,industry,bio-engineering,irrigation,blood flow,biophysical sciences,and especially in the field of geothermal sciences.Nadeemet al.[24]reported Casson fluid flow in three dimensions by a stretching permeable sheet. Xuet al.[25]examined the influence of porosity on natural convective transport in fluid flow by metal-foam cavity. Hayatet al.[26]examined the impact of porosity on stagnation point flow of magnetohydrodynamic viscous material by a vertical extending sheet.Analysis of heat transportation in the fluid flow due to an exponentially stretched porous surface is reported by Mandal and Mukhopadhyay.[27]The characteristics of the Maxwell fluid over a porous surface is investigated by Bhattiet al.[28]Improvement in the thermal performance of nanomaterials in the presence of solid nano-sized particles and foam metals is reported by Xuet al.[29,30]Khanet al.[31]numerically examined Darcy–Forchhemier flow along with heterogeneous–homogeneous reactions. Mathematical modeling and theoretical investigation of convective nanofluid flow by porous surface with phase interactions is reported by Xinget al.[32]Xuet al.[33]reported the impacts of permeability on convective heat transportation in fluid flow by metal-foam duct.

The thermal energy per unit temperature that is unavailable for valuable work is the entropy (irreversibility) of system. In other words the total rate of disorder in a system is entropy. In any thermodynamic arrangement, chemical reactions,internal fluid friction,radiation effects,viscous dissipation, magnetic field, porous medium internal energy losses,which generate entropy in the system. Entropy generation gained extraordinary attention in various fields of science and engineering such as heat exchangers, electronic device cooling,and turbomachinery. Poulikakos and Bejan[34]introduced a general framework for irreversibility optimization to study the thermal characteristics of conventional fins of different kinds. In this study the first law of thermodynamics is used to study the different shape of fins and second law of thermodynamics is utilized to optimize the entropy of fins in terms of dimension and length. Latter on Bejan[35]developed a model based on both thermodynamics and system irreversibility. Now, the entropy generation due to nanomaterial flow is becoming an interesting field of research. Wanget al.[36]reported Couette flow behavior and estimated entropy generation (EG) for both of heat transfer and shear. Heat transport properties and EG were studied through the second law of thermodynamics and the results obtained are equated with the flow of CuO, Ag, and Al2O3nanoliquid by Jafarmadaret al.[37]Khanet al.[38]inspected the EG in MHD Carreau nanomaterial flow by a stretched surface subject to viscous dissipation and nonlinear thermal ration. Features of dissipative unsteady flow and EG with thermo-diffusion and diffusion thermo effects are reported by Hayatet al.[39]Recent developments on entropy generation are described in Refs.[40–50].

The current work aims to analyze the flow of Jeffrey nanofluid over a stretched configuration with the entropy generation and various thermal features. The motivating and distinct aspects of current analysis are summarized as follows:

(i) Examination of the rheological significances of Jeffrey nanofluid subject to the magnetic force and porous space.

(ii) The applications Bejan number and entropy generation are taken into account with optimized applications.

(iii) The novel significances of viscous dissipation and thermal radiation are also utilized to examine the combined heat/mass transport.

(iv) Convective boundary conditions are imposed to improve the transportation process.

(v) Some studies have already been reported in the literature regarding the flow of Jeffrey nano-materials over a stretched surface, however, the flow of Jeffrey nanofluid in presence of such thermal consequences has not been performed in the literature. Therefore, the current investigation aims to fill this research gap. The solution procedure is based on analytical expressions employing a homotopic convergent scheme.

(vi) Current thermal flow model conveys many applications in the improving heat transfer mechanism, solar energy applications,thermal systems,energy production,energy consumptions,etc.

2. Problem formulation

Here MHD two-dimensional convective transport of Jeffrey nano-material with entropy generation assessment is presented with convective boundary constraints. For electrically conducting fluid,the magnetic force impact is assumed in the normal direction with uniform magnetic field strengthB0as shown in Fig.1.

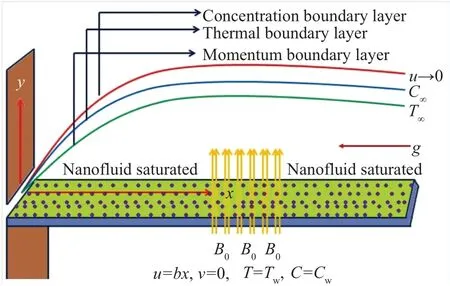
Fig.1. Flow geometry.

The role of the induced magnetic force is ignored due to small Reynolds number assumptions. Furthermore, the energy equation is modified by considering the viscous dissipation and thermal radiation. The important prospective of thermophoretic features and Brownian movement are utilized.The linear configuration(stretched surface)attain uniform velocityuw(x)=bx.The mathematical model for the Jeffrey nanofluid after employing boundary layer assumptions is given as follows:

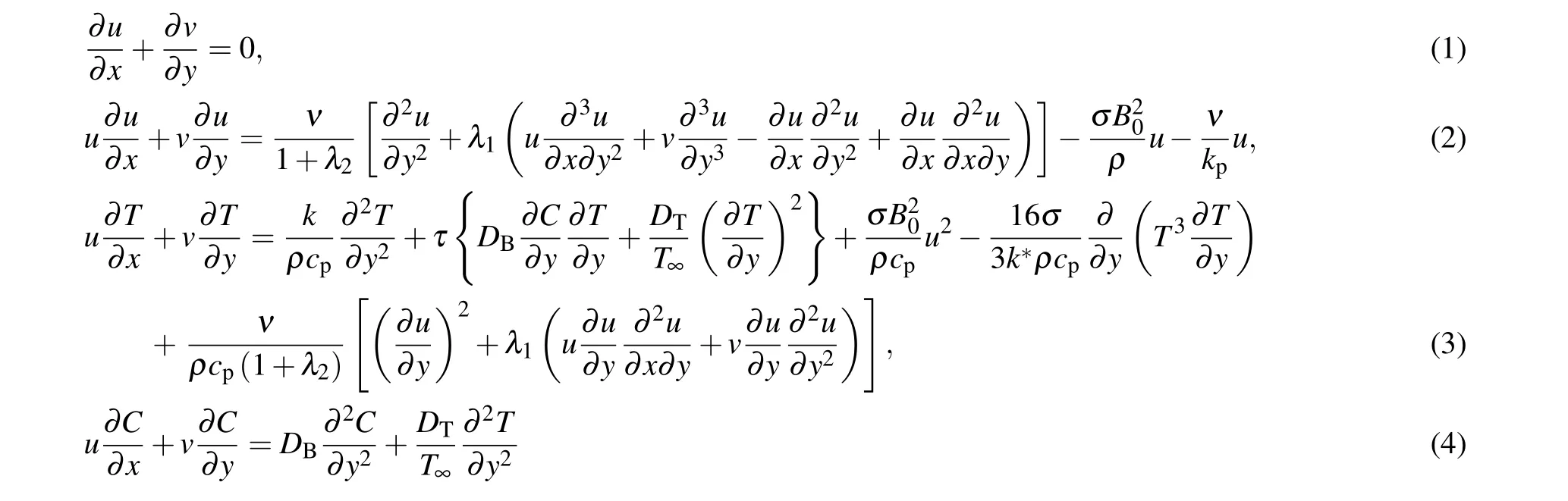
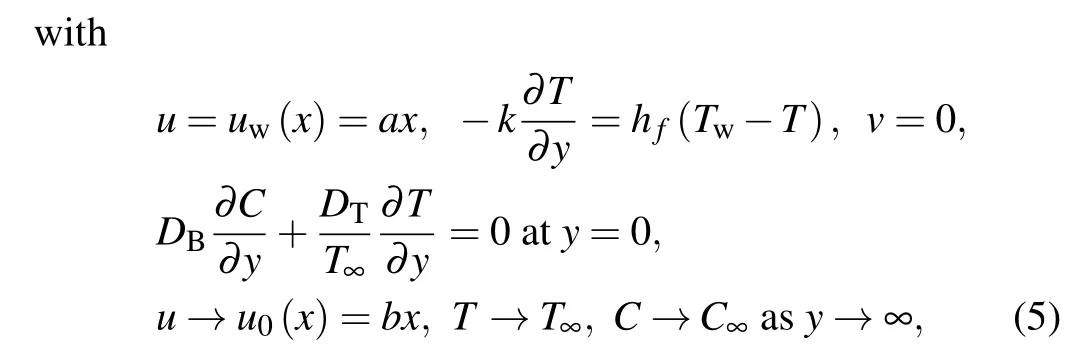
whereB0is the magnetic field, (u,v) is the velocity alongxandydirections, (Tw,Cw) is the surface temperature and concentration,λ1is relaxation time,DBis the coefficient of the Brownian motion,λ2is the relaxation to retardation time ratio,cpis fluid specific heat,kpis permeability,DTis the thermophoretic diffusion,νis the kinematic viscosity,bis the sheet stretching rate constant,(T∞,C∞)is the ambient temperature and concentration,k?is the absorption coefficient,σis the electric conductivity,τis the heat capacity ratio,hfis the convective heat transfer,kis thermal conductivity,qmis the local mass flux,Hais Hartman number,βis Deborah number,Ais the ratio parameter,k1is the porosity parameter,Nbis Brownian dispersion variable,Rdis the radiation parameter,Pris Prandtl number,Ntis thermophoresis variable,Ecis Eckert number,Nris temperature difference ratio parameter,Scis Schmidt number,Shxis Sherwood number,C fxis he skin friction,Nuxis Nusselt number,Reis Reynolds number,Bris Brinkman number,εis concentration difference variable,?is the temperature difference parameter,λ3is diffusive variable,Biis thermal biot number,μis the dynamic viscosity,ηis a dimensionless variable,Tis the nanofluid temperature,θ(η)is the dimensionless temperature,?(η)is the dimensionless concentration,f′(η)is dimensionless velocity,Cis the nanofluid concentration,andqwis the surface heat flux. Considering

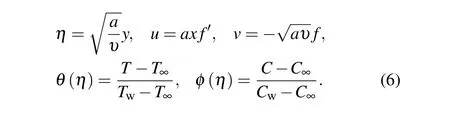
Using Eq.(6),equations(2)–(5)take the form

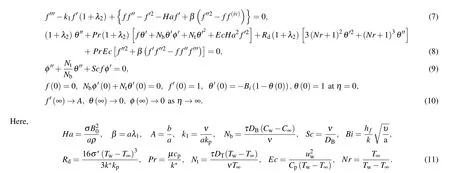
2.1. Physical quantities

The coefficient of skin friction (C fx), Sherwood (Shx),and Nusselt(Nux)numbers are mathematically defined as

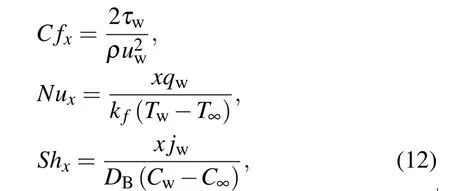
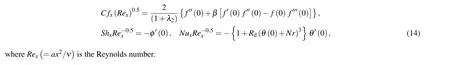
2.2. Entropy rate and Bejan number

Mathematically

3. Solution procedure

The set of dimensionless equations (7)–(9) are locally similar so the analytical solution is computed by using the homotopy analysis method (HAM). The pioneer directions and mathematical formulation of this scheme was originally proposed by Liao[51]and later many interesting developments and generalizations on this method have been presented by various researchers.[41,45,48]The relevant initial guesses and linear operators are taken as

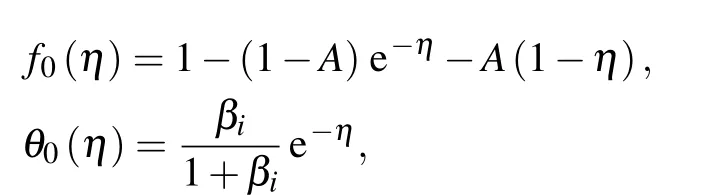
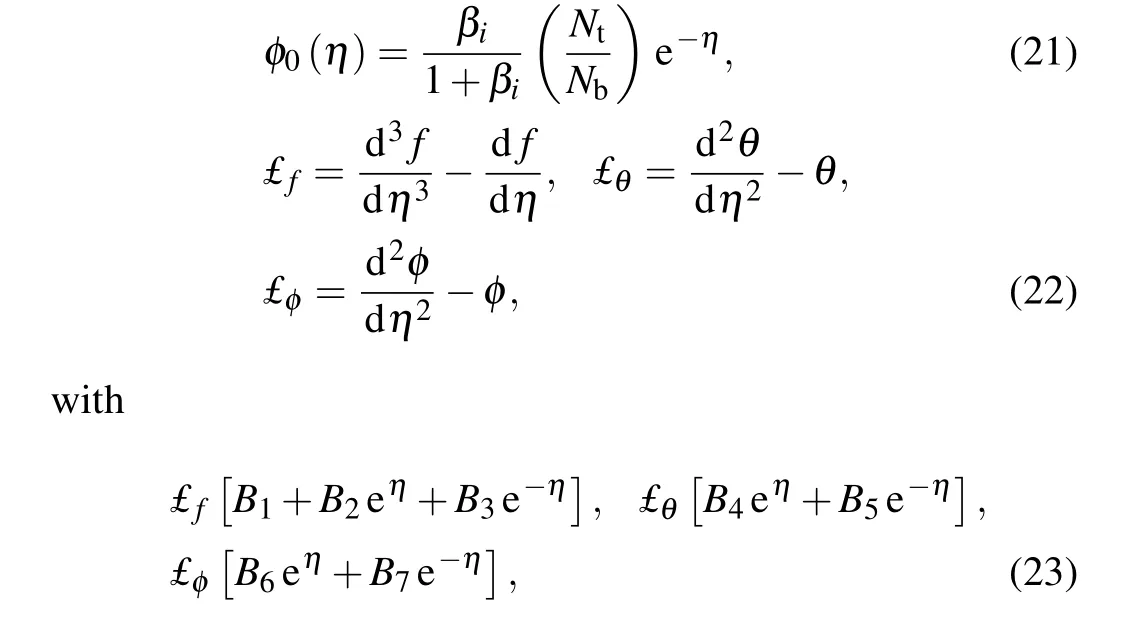
whereBi(i=1–7)are constants.

4. Convergence analysis

The assisting variables ˉhf, ˉhθ, and ˉhφplay a vital role in regulating the convergence of homotopic expressions. Figure 2 is plotted to find the ranges of assisting parameters after the 14-th order of approximation whenλ2=A=β=k1=0.1,Ec=0.3,Ha=Nt=Bi=0.2,Rd=0.4,Nb=0.7,Sc=Pr=1.0,andNr=1.1.

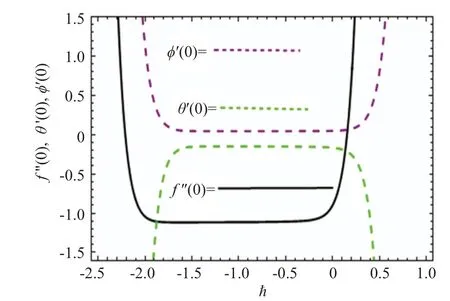
Fig.2. The ˉh curves for f′′(0),θ′(0),and φ′(0).

The convergence regions of velocity, temperature, and concentration functions are?1.8≤ˉhf ≤?0.4,?1.5≤ˉhθ ≤?0.3,and?1.6≤ˉhφ ≤?0.2. The convergence of the HAM solution is presented in Table 1.

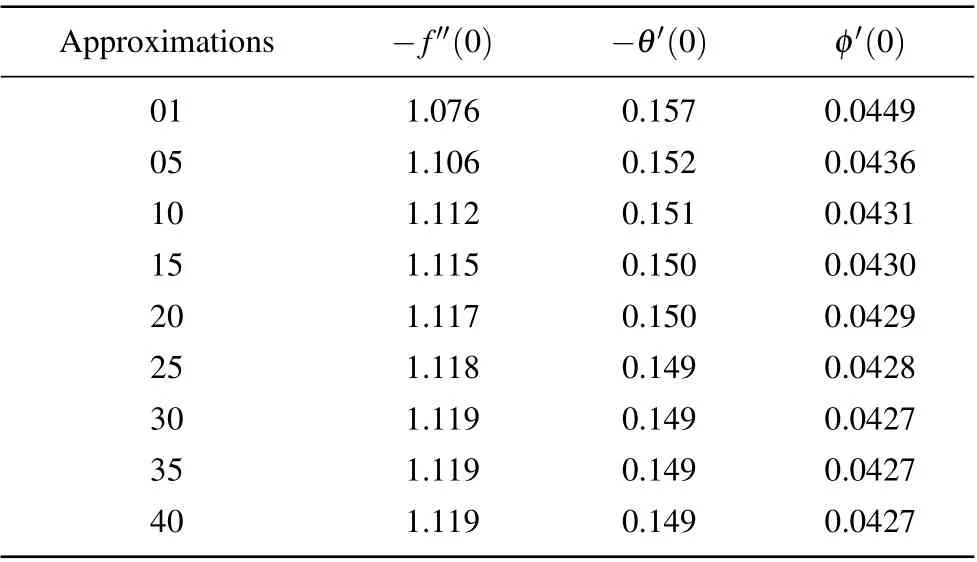
Table 1. Computational outcomes for f′′(0), φ′(0), and θ′(0), when λ2 =A=β =k1 =0.1,Ec=0.3,Nb =0.7,Rd =0.4,Sc=Pr=1.0,Ha=Nt=Bi=0.2,and Nr=1.1.

5. Solution validation

After successfully simulating the analytical expressions in the previous section,we aim here to confirm the computed solution. To this end, the present results have been verified by comparison with the continuation of Turkyilmazoglu[52]in Table 2.There is an excellent agreement between both studies.

Table 2. Comparison of f′′(0)with λ2=β =k1=A=0.

6. Discussion

6.1. Velocity profile

In this subsection salient features of the Deborah number(β),Hartman number(Ha),permeability parameter(k1),and ratio parameter(A)on the Jeffery nanofluid velocity(f′(η))are discussed. The effect ofβonf′(η)is shown in Fig.3(a).The fluid velocity increasesversushigherβ. Physically,βhas direct relation with the sheet stretching rate,so increasingβcauses an increase in the sheet stretching rate, as a result the fluid velocity inside the boundary layer upsurges and the thickness of momentum boundary layer also increases. Velocity field decays via higher fluid parameter, since fluid parameter has inverse relation with retardation time which means that retardation time decay with higherλ2(Fig. 3(b)). A decrease in velocity with increasing Hartman number is observed in Fig.3(c). Physically,for higherHa,more Lorentz force is produced,which is a restive force acting on the fluid opposite to the flow. Hence the fluid velocity retards with risingHa.Figure 3(d)explores the influence of the porosity variable on velocity field. In fact the velocity has an inverse relation with permeability, thusf′(η) and momentum layer thickness decease with increasingk1.The influence of the ratio variable on the velocity is depicted in Fig.3(e).

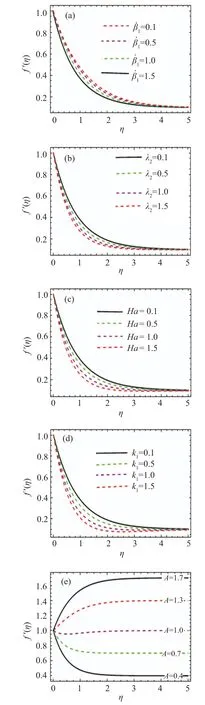
Fig.3. Impacts β (a),λ2 (b),Ha(c),k1 (d),and A(e)on f′(η).

It can be seen from this figure that forA<1,the velocity field and the layer thickness increase and forA>1,the velocity decreases and layer thickness increase whereas forA=1 the boundary vanishes since forA=1 the fluid velocity and sheet stretching velocity becomes the same.

6.2. Temperature profile

Figures 4(a)–4(h) presented to show the behavior of the temperature fieldθ(η)with fluid parameter(λ2),the Prandtl number (Pr), the thermophoretic variable (Nt), the ratio of temperature(Nr),the Brownian movement(Nb),the radiation parameter(Rd),and the thermal biot number(Bi).

Figure 4(a)explores the characteristics ofθ(η)with increasing thermal layerλ2, the thickness inflates with higherλ2since for higherλ2retardation time deceases which causes an increase in the temperature field and thermal layer. The variation inθ(η) for higherPris depicted in Fig. 4(b). The nanofluid temperature decreases at higherPr. As we know thatPrhas an inverse relation with thermal diffusivity, so an increase inPrmeans a decrease in fluid thermal diffusivity.Subsequently thermal field and associated layer width falling down with risingPr. The radiation effect on the thermal field is studied in Fig.4(c). As expected the thermal field and layer thickness increase for higherRd.Physically,the radiation variable describes relation of heat transfer conduction to transfer of thermal radiation,so an increase inRdslows down the thermal radiation transmission, which ultimately favors temperature increase. The behavior ofθ(η) withEcis displayed in Fig. 4(d). The observations reveal thatθ(η) is a decreasing function ofEc.

Figure 4(e)elucidates the impact of the Brownian movement of nanoparticles on the thermal field. Clearlyθ(η) increases with higherNb, because the Brownian phenomenon involves the random movement of nanoparticles which increases with temperature profile. The graphical trend explored in Fig. 4(f) shows an increasing variation in nanofluid temperature due to specified values ofNt. Physically, the thermophoretic force is a force which extracts the nanoparticles from a hot surface and pushes them to a region of low temperature and consequently an improved heat transfer phenomenon results.

Figure 4(g)shows the influence ofNronθ(η),obviously the thermal field diminishes for higherNr. Wall temperature(Tw) is higher than ambient temperature andNris inversely proportional toTw?T∞,thus for higherNrtheθ(η)decreases.Variation ofθ(η) with increasing values ofBiis plotted in Fig. 4(h). The nanofluid temperature and thermal layer decreases with higherBi.

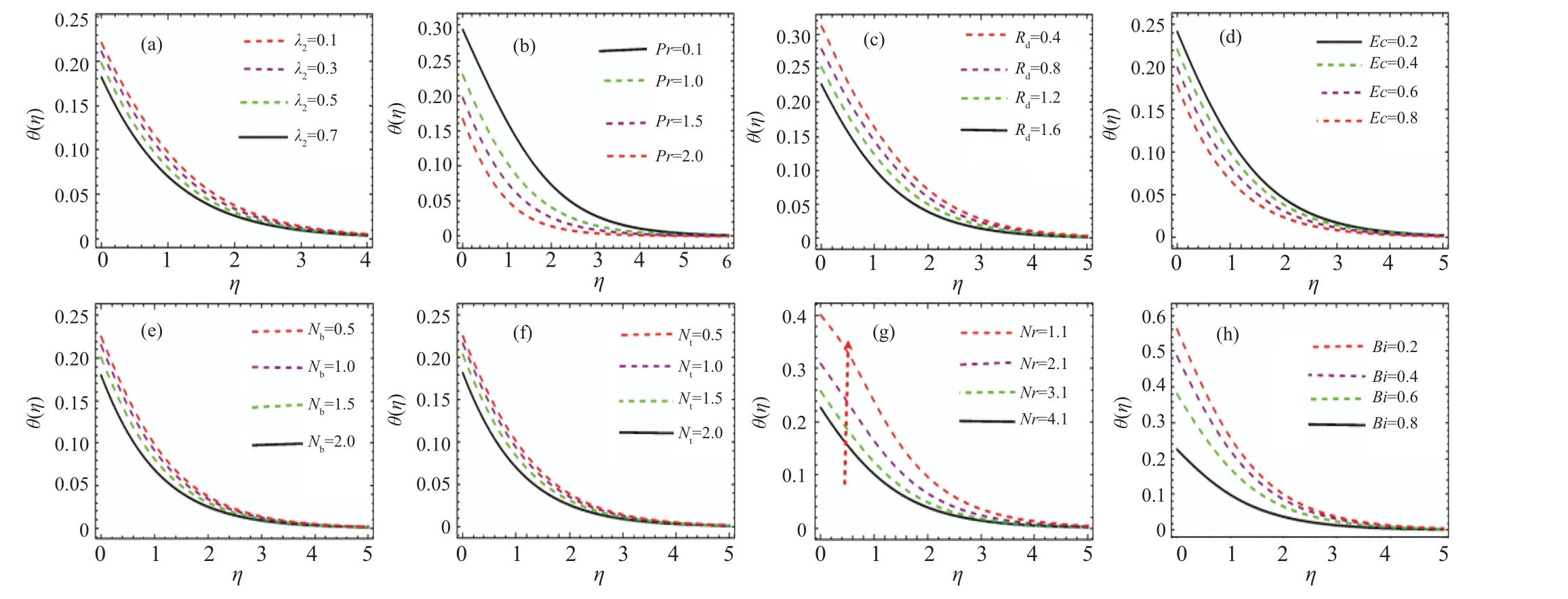
Fig.4. Impacts of λ2 (a),Pr(b),Rd (c),Ec(d),Nb (e),Nt (f),Nr(g),and Bi(h)on θ(η).

6.3. Concentration profile

Features of the mass concentration(?(η))versusBrownian dispersion(Nb),Schmidt number(Sc),and thermophoresis diffusion variable (Nt) are studied in this subsection through Figs.5(a)–5(c).

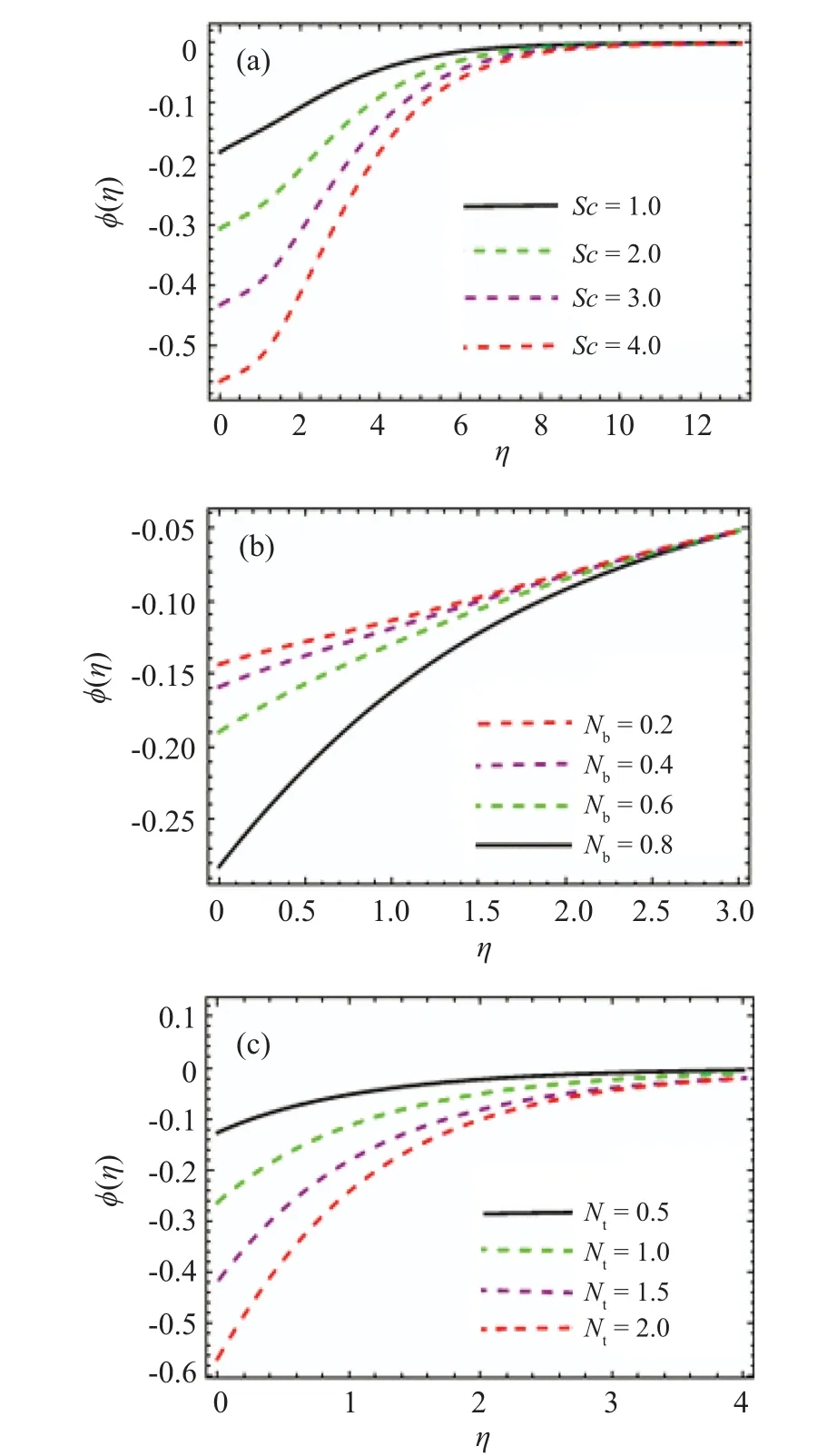
Fig.5. Impacts of Sc,Nb,and Nt on ?(η).

The behavior of?(η)for increasingScin Fig.5(a)indicates that higherScreduces mass concentration.Physically,Screpresents the ratio of momentum to mass diffusivities,so increase inScresults in an increment in momentum diffusivity while mass diffusivity diminishes. Ultimately a reduction in mass concentrations is observed. Figures 5(b)and 5(c)shows the influence ofNbandNton mass concentration. Clearly?(η)increases withNband diminishes with higherNt.

6.4. Physical quantities

In this subsection, the behavior of physical quantities,i.e.,skin friction(C fx),Nusselt number(Nux),and local mass transfer(Shx)versusinfluential variables are presented graphically.

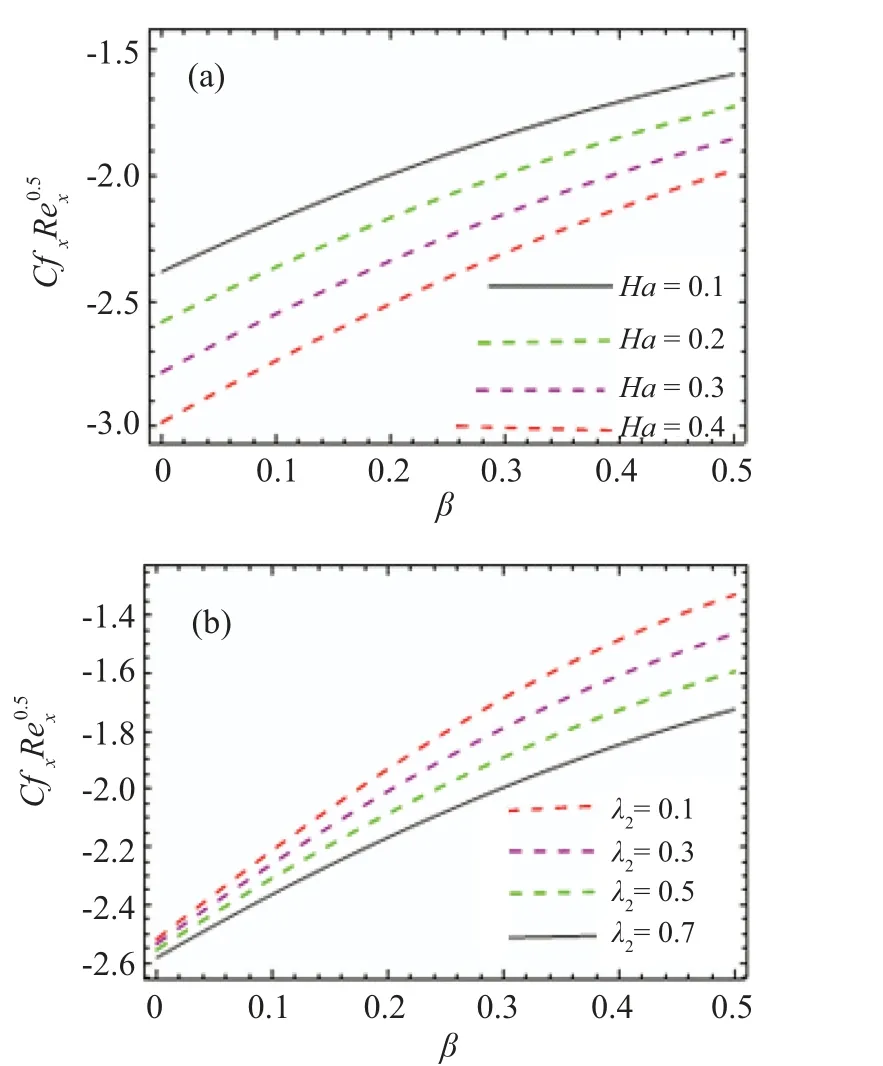
Fig.6. Effects of Ha and β (a),λ2 and β (b)on C fxRe0.5x .

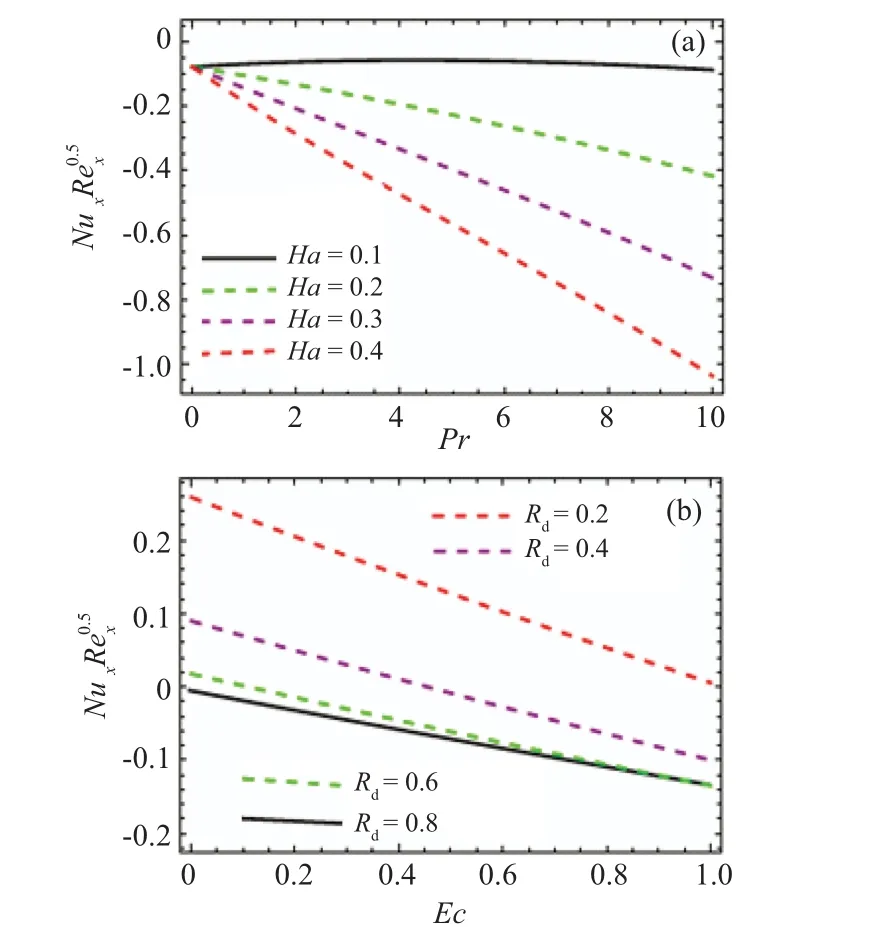
Fig.7. Effects of Ha and Pr(a),Rd and Ec(b)on NuxRe?0.5x .

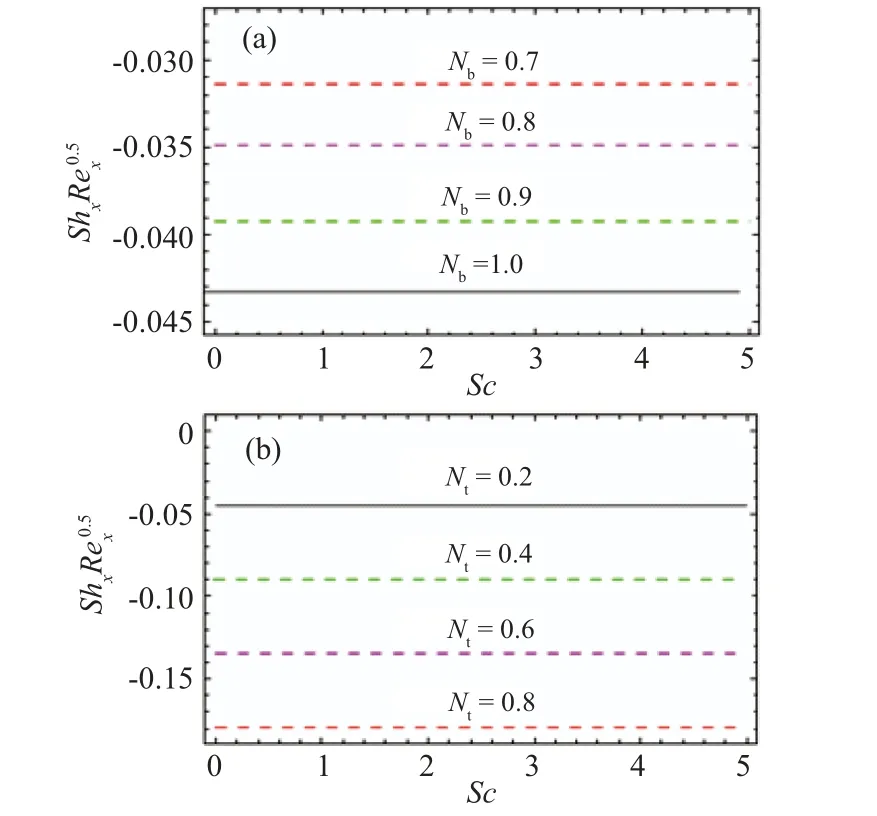
Fig.8. Effects of Nb and Sc(a),Nt and Sc on ShxRe?0.5x .

The graphical observations presented in Figs. 6(a) and 6(b)reflect the influence ofHa,β,andλ2on skin friction.The magnitude of the skin friction diminishes for higher Hartman and Deborah number andC fxincreases with the fluid parameter and Deborah number.The characteristics ofNux versus Pr,Ha,Rd, andEcare studied through Figs. 7(a) and 7(b). The Nusselt number monotonically decreases for increasing values ofPrand fixed values ofHa(see 7(a)). From Fig. 7(b),it can be seen that the Nusselt number decreases with higher radiation variable and Eckert number.Figures 8(a)and 8(b)explore the behavior of the Sherwood number againstNb,Nt, andSc.The magnitude of the Sherwood number increases with largerNbandScwhile a declining change is noted due to variation ofNtandSc.

6.5. Entropy generation and Bejan number

In this subsection the impact of significant variables on Bejan number (Be) and entropy (NG) is analyzed and discussed graphically through Figs. 9(a)–9(f). The influence of Brinkman number on entropy and Bejan number is demonstrated in Figs.9(a)and 9(b). It is observed from these figures that entropy increases for higher Brinkman number(Br)while the Bejan number decreases.Physically,Brinkman number attains opposite relations with thermal diffusivity which means that maximum values ofBrentropy generation increases and the Bejan number decreases. Figures 9(c) and 9(d) demonstrates the behavior ofNGandBefor increasing values of Jeffrey fluid variable(λ2). It is observed from these figures that the trend for bothNGandBeis to increase at higherλ2. Figures 9(e)and 9(f)display the effect of radiation constant(Rd)onNGandBe. BothNGandBeincrease with higherRd. In factRdhas direct relation with bothNGandBe,so for higherRdradiation emission increases. ConsequentlyNGandBefor higherRd.

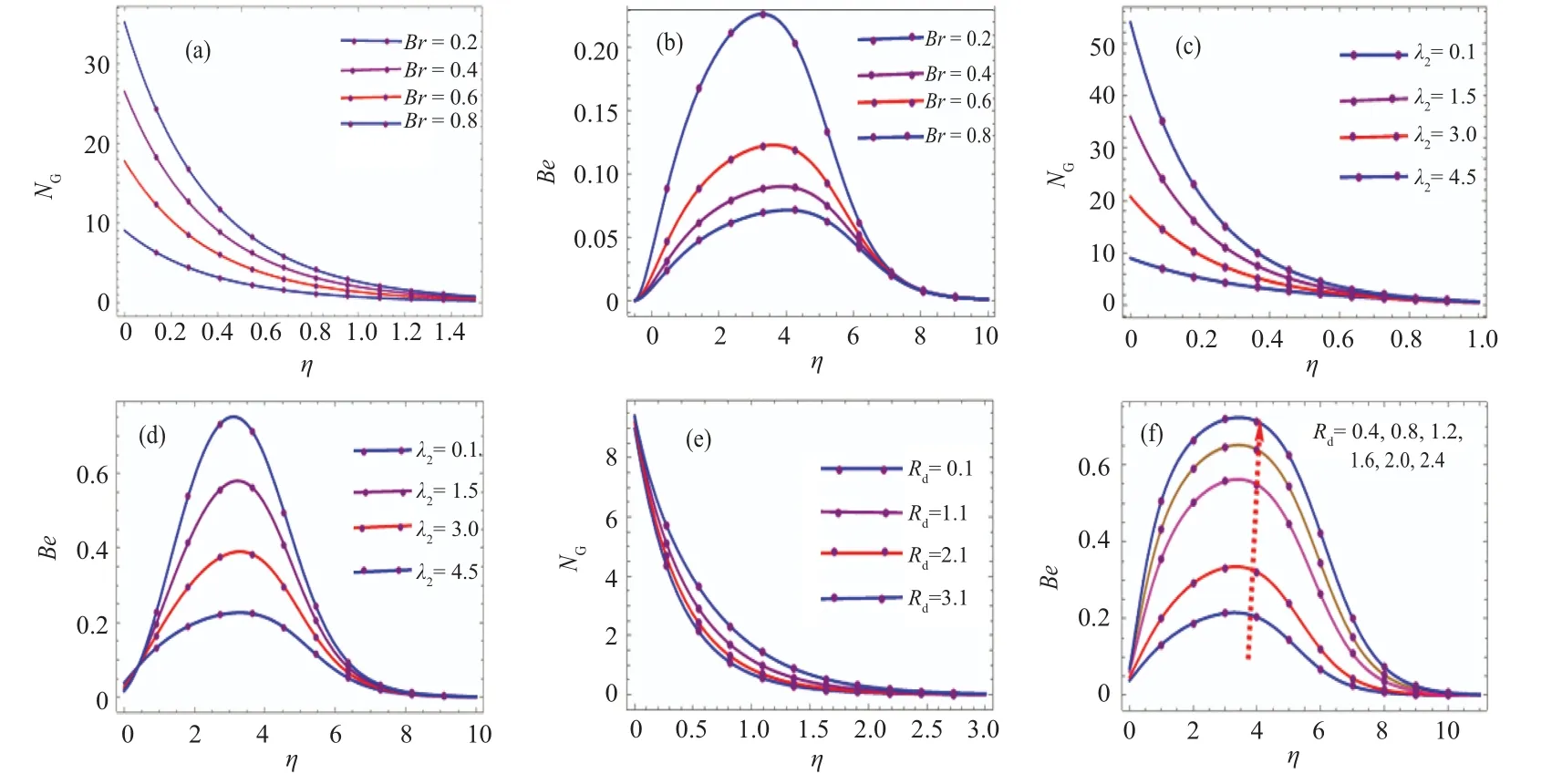
Fig.9. Behavior of NG and Be versus Br,λ2,and Rd.

7. Conclusions

The mathematical modeling and analysis for the flow of Jeffrey nanofluid with entropy generation features,Joule heating and thermal radiation has been presented. The porous stretched surface subject to the magnetic force induces the flow. The analytical procedure based on a convergent scheme is followed to compute the solution. The solution accuracy is ensured and compared with previous research data. The summarized observations are listed below.

(i) A declining trend in the velocity profile is observed with permeability of porous space,Deborah number and fluid parameter.

(ii) An increase in nanofluid temperature is related to the Biot number,fluid constant,radiation parameter,and temperature difference ratio parameter.

(iii) The skin friction coefficient decreases with higher Hartmann number and Deborah number while a monotonically increment is noticed for the fluid parameter.

(iv) A lower change in local Nusselt number is observed due to the change in Hartmann number.

(v) A declining impact of Brinkman number on entropy generation and Bejan number is noticed.

(vi) Entropy generation and Bejan number increase with fluid constant and radiation parameter.

Acknowledgment

This research was supported by Taif University Researchers Supporting Project (Grant No. TURSP-2020/217),Taif University,Taif,Saudi Arabia.