Chenhao Liu(劉晨浩), Haoshu Jin(靳昊澍), Hui Liu(劉輝), and Jintao Bai(白晉濤)

Institute of Photonics&Photon-technology,Northwest University,Xi’an 710069,China

Keywords: optical frequency combs,optical injection locking,dual-frequency lasers

1. Introduction

The optical frequency combs (OFCs) have broad applications,[1]including optical atomic clocks,[2–4]microwave photonics,[5]calibration of astronomical spectrographs,[6]LiDAR,[7]frequency comb spectroscopy,[8]and attosecond science.[9]From the view of frequency domain, OFCs are consist of a large number of modes with equidistant frequencies and fixed relative phase. Up to now, this kind of optical spectra can be implemented mainly by three technologies that is mode-locked laser,[10]electro–optic comb generator,[11,12]and microresonator.[13]Typically, these OFCs require cavity resonance to enhance optical oscillations, but the freedom of comb line spacing is largely limited. In fact, OFCs without optical cavity are possible, for example the electric–optic frequency comb based on the cascading of multi-modulators.However, the modulators may also impose some limitations,such as modulation bandwidth and the requirement for highdepth modulation.

An interesting proposal to generate OFC without optical resonator and modulator is to transform a dual-frequency beat signal into a train of pulse through the propagation in nonlinear optical fiber.[14–19]However, its development is hindered due to the requirements of high power for pumping,long path for spectral broadening,sophisticated dispersion management,and low-noise dual-frequency lasers,etc.

Fortunately, some technological advances are gradually breaking these restrains, making that proposal still quite attractive. To this end,the following investigation refers two interesting technologies. The first one is the the low-noise dualfrequency laser(DF-laser)that can be achieved by sustaining two lasers in a common cavity. Such kind of dual-frequency lasers can be realized in platforms of VECSEL,[20–25]solidstate laser,[26,27]fiber lasers,[28,29]etc. By this device, lownoise optically carried radio frequency(RF)can be generated even in free running due to the elimination of the common noises. This dual-frequency is equivalent to singe side-band modulation but with a high modulation depth which is closing to one. Moreover,the optically carried RF can be broadly tuned without the limitation of modulation bandwidth. The second one is the multimode optical injection locking (OIL)which can be an effective way of wave-mixing. It has been demonstrated that optical injection of OFC into semiconductor lasers can broaden the spectrum effectively due to the strong four wave-mixing.[30,31]

This paper reports an investigation of the possibility to generate an OFC by optical injection locking a semiconductor laser to a DF-laser by numerical simulations. In addition to the process of dual-frequency optical injection, the simulations also consider the random noises from spontaneous emissions. The evolution of output power, carrier number,and optical phase are simulated, from which the spectra, and phase/intensity noises can be derived. The pulse width of the OFC generated with this way can be less than 30 ps. Moreover, the pulse shape can be controlled to be Gaussion-like.Comparing to the way of sending the DF-laser to high nonlinear fiber directly, optical injection allows to start from low power,or to reduce the length of nonlinear fiber thereby alleviate the suffering from dispersion induced phase mismatching.We thus expect it can offer a good initial stage of OFCs generation with DF-laser,whose spectra can be further broadened in nonlinear waveguides,giving a broadband OFC without external modulation and can be agile in central wavelength and comb spacing.

2. The model of dual-frequency laser optical injection

3. The simulation results and discussion

To help in understanding the dynamics,the optical injection of dual-frequency laser is compared to the instances of single-frequency laser (SF-laser) injection, and free-running,as shown together in Fig. 1 to indicate the difference. The spectra in Fig.1(a)show that two peaks are sided around the optical carrier when a SF-laser is injected, whereas the random noises are substantially suppressed comparing to the freerunning laser. The two side peaks indicate the strong relaxation oscillation under the high seeding power OIL. We call these peaks as relaxation oscillation peak(RO-peak). In fact,injected light-induced pulsations (ILIP) may happen according to the well-known theory of SF-laser injection.[33]With the knowledge of this phenomenon,the beat-note frequency of the injected DF-laser is chosen to coincide the RO-peak, leading to an efficient generation of new tones. These new tones are the results of four wave-mixing(FWM)effect in semiconductor lasers,which has been explained by the light induced gain grating and index grating.[34]Figure 1(a)shows that there are 10 tones above the random noises after the DF-laser injected with a seeding power ofK=10?5/20. The reason why the efficient FWM happens can be explained by Fig. 1(b) which shows the carrier population pulsation and the pulsed modulation of optical phase, corresponding the dynamic gain grating and index grating. To distinguish it from SF-laser ILIP,we call it DF-laser ILIP. Moreover, the tones are symmetrically distributed around the optical carrier. This symmetry is obtained by the balance between two asymmetries. One comes from the asymmetry injection of the DF-laser, since one component of the injected light is used for locking the slave laser, the other component is right sided, as indicated by the arrows in Fig.1(a). The other asymmetry comes from the gain asymmetry introduced by Henry’s factor,which leads to the higher gain at lower (left) frequencies. Thanks to this symmetry spectrum, the generated pulse is Gaussian-like, as shown in Fig.1(b). Figures 1(c)–1(d)show the power spectral density of the phase and intensity, which illustrates that the random noises around the RO-peak are greatly suppressed and replaced by a new tone. It means that the RO-peak is locked to the beat-note frequency and gives a low-noise pulse train.This is a big difference between the DF-laser ILIP and SFlaser ILIP. However, except the region nearby the RO-peak,random noises in DF-laser injection are more than that of SFlaser injection,which can be attributed to the interference between the comb lines.

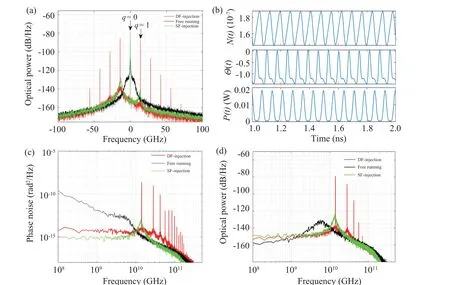
Fig.1. A simulation of dual-frequency injection(DF-injection)to a single-mode semiconductor laser: (a)the spectra; (b)the evolution of carrier number N(t), output power P(t), and the optical phase Θ(t); (c) the power spectral densities of the phase noises; (d) the power spectral densities of RINs. The circumstances of free running and single-frequency injection(SF-injection)are shown together. The parameters used in this simulation are listed in Table 1.

Table 1. Parameters used in the simulations for Fig.1.

The above simulations raise a question that whether it is necessary to lock the RO-peak. To investigate this problem,the beat-note frequency is tuned from 2 GHz to 14 GHz, as shown in Fig.2. When the beat-note frequency is well below RO-peak frequency, lots of tones are generated and the ROpeaks are overwhelmed by the new tones.However,RO is embedded in each pulse waveform,so that the pulses are severely deformed to be away from Gaussian-like.As the beat-note frequency is close to RO-peak frequency,the pulse form becomes more Gaussian-like, giving a higher peak power. However,when beat-note frequency is well above RO-peak frequency,the RO-peaks are set to be free, giving some random noises and reducing the efficiency of the FWM. Therefore, choosing the beat-note frequency closing to RO-peak frequency is important for the efficiency of FWM and the random noise suppression.

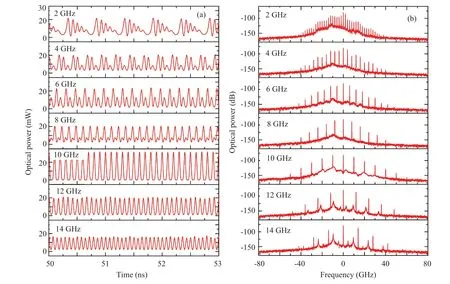
Fig.2. The dependence of pulse shape and spectra on the beat-note frequency of the injected DF-laser: (a)the output pulse train,(b)the spectra. In these simulations,the value of seeding power is K=10?10/20. The parameters not indicated here are the same as those used in the simulation of Fig.1.

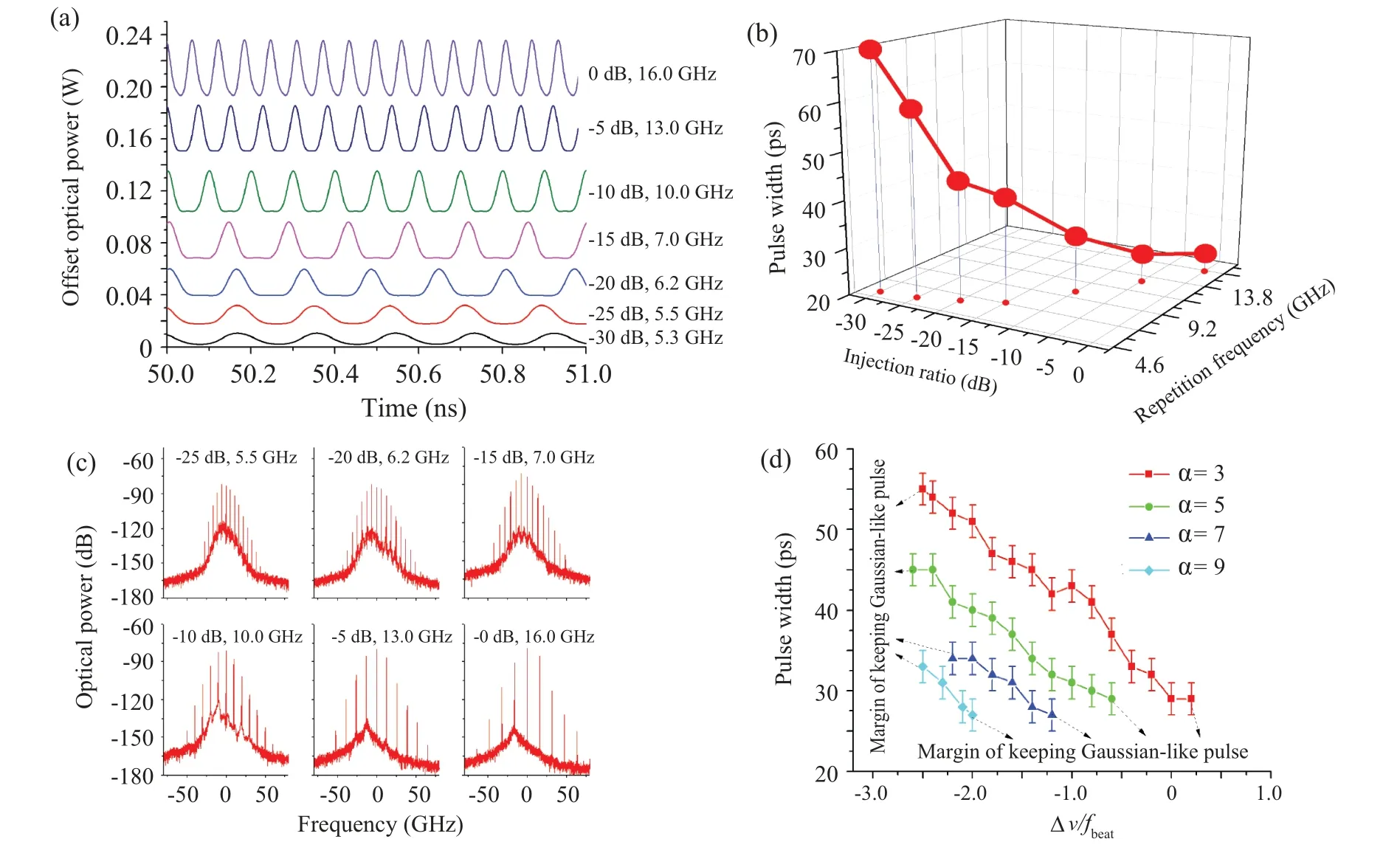
Fig.3. The simulations with Gaussian-like pulse output: (a)the pulse train,(b)the pulse width,(c)spectra at different combination of seeding power and beat-note frequency,(d)the dependence of the pulse width of Gaussian-like output on the value of Henry’s factor α. The injection ratio in unit dB is equal to 20log10(K). ?ν denotes the free running slave laser frequency detuned from the master laser frequency of q=Q1 =0, fbeat is the beat-note frequency.The parameters not indicated here are the same as those used in the simulation of Fig.1.

It seems that beat-note frequency is constrained by the RO-peak frequency. This constrain can be lifted by the freedom of varying the seeding power. Figure 3(a) shows an example where Gaussian-like pulse output can be achieved in the repetition frequency range from 5.3 GHz to 16.0 GHz by varying the seed power. The corresponding pulse widths are plotted in Fig. 3(b), showing that not only the repetition rate becomes higher,but also the pulse becomes shorter. Pulses as short as below 30-ps is possible. Additionally,higher seeding power can also suppress the random noises in a higher degree,as shown in Fig.3(c). However, when the repetition rate frequency goes higher,the tones become fewer,which is limited by the bandwidth of single longitudinal mode. As a result,the pulse width is limited to be about 30 ps. Generally, it is desirable to use the lowest possible seeding power to generate optical frequency combs with the lowest possible noise.Given these requirements,the 10-GHz is a value approaching the optimum beat-note frequency,where the seeding power is only about?10 dB,and the width of Gaussian-like pulse can reach the 30-ps limitation. Additionally, the value ofris another variable to change the RO-peak frequency,but its effect is small as will be shown in Fig.4.In principle,the values ofτpandτncan also be used to change the RO-peak frequency,but they are not controllable for a given DFB semiconductor laser.Although these two intrinsic parameters are engineerable,the typical values are more practical for experiments.

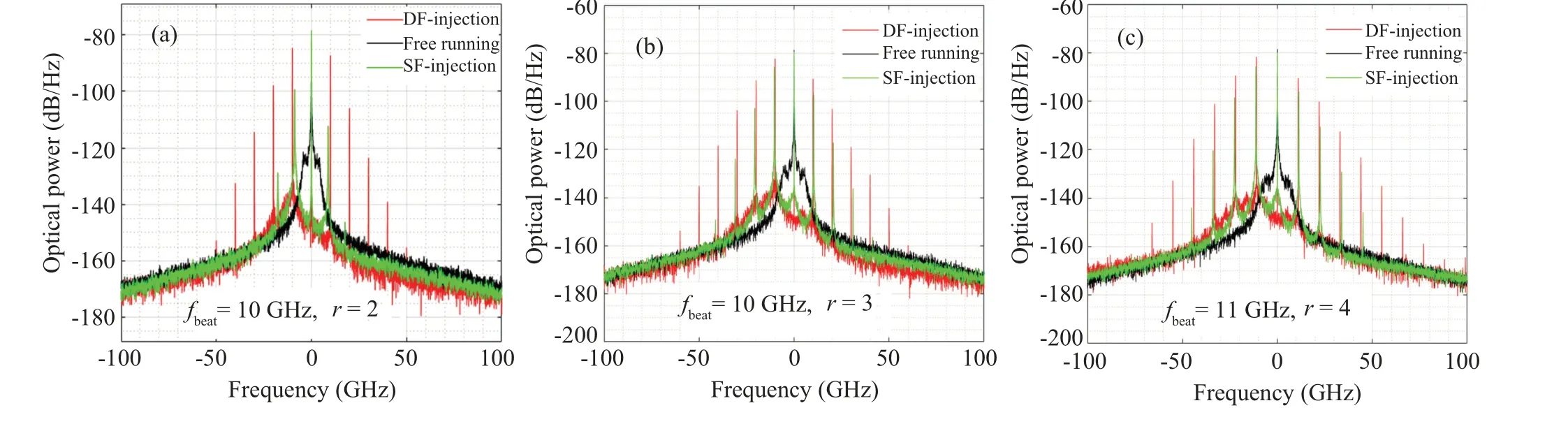
Fig.4. Enhancement of the ILIP by increasing the excitation ratio r. Panels(a)–(c)show the spectra of the simulation with r=2,3,and 4,respectively. The corresponding pulse width is 36 ps,30 ps,and 27 ps,respectively. The parameters not indicated here are the same as those used in the simulation of Fig.1.

Another import aspect for OIL is the detuning. Figure 3(d) shows that the Gaussian-like pulse form can be kept in the detuning range of ?ν/fbeat=?2.5 to ?ν/fbeat=0.2 whenα=3,where ?νdenotes the free running slave laser frequency detuned from the master laser frequency ofq=Q1=0,fbeatis the beat-note frequency.It suggests that the working region is shifted to the negative detuning where the gain is higher due to the amplitude/phase coupling effect. Therefore, as the value ofαincreases,the preference for negative detuning becomes more, but the working range for Gaussian-like pulse output becomes smaller. However, the detuning towards positive can give shorter pulses because the lower gain at higher optical frequency can be compensated by the injected field,leading to a broader spectrum.

Since RO can help to build shorter pulse, it makes sense to investigate the OIL under stronger RO.Figure 4 shows the results when the carrier excitation ratiorchanges.One can see that stronger RO-peak can be built with higher value ofr. If thervalue is high enough,some comb-like tones can be built even with SF-laser injection,which indicates the happening of SF-laser ILIP. When the DF-laser is injected into, the RO is locked to the injected light and builds shorter pulses.

4. Conclusion

In conclusion, the optical injection locking of singlemode semiconductor lasers to DF-lasers is studied by numerical simulation. This optical injection can generate an OFC due to the efficient FWM effect created by the nonlinear gain medium inside the semiconductor laser. Choosing the beatnote frequency of the DF-laser closing to RO-peak is very important for generating Gaussian-like pulses. Moreover, the RO can be locked to the beat-note frequency of the DF-laser,thus can suppress the random noise greatly. The RO-peak frequency can be tuned by changing the seeding power. Therefore,the repetition rate of the Gaussian-like pulse can also be tuned this way. Low repetition rate gives more random noise,but higher frequency creates less new tones. Gaussian-like pulse shape can be kept within a certain range of detuning,and this detuning tend to be negative due to the gain symmetry. However, the shortest pulse happens at the margin towards to positive. Additionally,stronger RO can be helpful to build shorter pulses, which can be realized by increasing the carrier excitation ratio. The RO-peak frequency can be tuned by the controllable variables,such as seeding power,and carrier excitation ratio,but also governed by the intrinsic parameters,including carrier lifetime,and photon lifetime inside the cavity. For the semiconductor laser exampled here, the beatnote frequency about 10 GHz is a value closing to the optimum,which can reach the pulse width below 30 ps. Although the pulse width cannot go down to femtosecond directly, this OFC can be furtherly broadened by nonlinear waveguides,for example the silicon-nitride waveguide.[35]Since there is no need of complex modulation or high-Q cavity, DF-laser optical injection can be a good option for realizing a simple,compact, low-cost, and robust OFC with a repetition rate around 10 GHz. This kind of OFC can be widely used in optical arbitrary waveform generation,microwave photonics,and optical coherent communication applications.[12]

Acknowledgment

Project supported by the National Natural Science Foundation of China(Grant No.62005215).