Jin-Fen Liu(劉進芬) Le Wang(王樂) and Sheng-Mei Zhao(趙生妹)

1Institute of Signal Processing and Transmission,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2Nanjing Tech University Pujiang Institute,Nanjing 211222,China

3Key Laboratory of Broadband Wireless Communication and Sensor Network Technology,Ministry of Education,Nanjing 210003,China

Keywords: orthogonal-triangular(QR)decomposition,ghost imaging,correlated imaging

1. Introduction

Ghost imaging (GI), also called correlated imaging, has attracted more and more attention in recent years.[1–21]The traditional GI (TGI) system consists of a signal beam and a reference beam. The signal beam,after illuminating on an object,is collected by a bucket detector without any spatial resolution. The reference beam, which never interacts with the object, is measured by a spatially resolving detector, such as a charged coupled device (CCD) or a complementary metal oxide semiconductor(CMOS)camera. By correlating the reference beam with the bucket signal, the ‘ghost image’ will be recovered in the reference beam. The first GI scheme was achieved based on the entangled-photon pairs, which were generated by spontaneous parametric down-conversion(SPDC).[1,2]Later, it was shown and demonstrated that GI could be realized with classical light sources,such as pseudothermal light,[3,4]true thermal light,[5–7]sunlight,[8]and even the screen of a television.[9]Besides,computational light patterns, produced by spatial light modulator (SLM) or digital mirror device(DMD),can also be used to realize GI.This latter approach is known as computational GI,whose light intensity detected in the reference beam is computed offline.[21]

Whereas, improving the imaging quality of GI is a key project.Recently,a variety of advanced basis illumination patterns based on ghost imaging methods have been proposed to enhance the imaging quality.[22–34]For example, Hadamard basis based ghost imaging and Fourier basis based ghost imaging,[22–31]which constitute a complete orthogonal set,can enhance the imaging quality and shorten the reconstruction time.However,if the speckle patterns are random,there is a high constant background that degrades the imaging quality.Lots of studies focus on improving the quality of the reconstructed images in the GI system with random patterns.[32–34]In 2014,peudo-inverse ghost imaging(PGI)[32]has been presented to enhance the peak signal to noise ratio (PSNR) and reduce reconstruction time for object reconstruction,by computing the pseudo-inverse of the matrix constituted by the row vectors of each speckle field.Later,singular value decomposition ghost imaging(SVDGI)[33]has been proposed to enhance the fidelity of GI by constructing a measurement matrix by using the singular value decomposition (SVD) transform. Besides, Gram–Schmidt ghost imaging[34]has been researched to enhance the efficiency of image acquisition, where a postprocessing method,instead of the pre-modulation method,has been introduced to orthonormalize the patterns in a rotating ground glass scheme by using Gram–Schmidt process. Because these techniques could put the random basis patterns constitute a complete orthogonal set,so they can improve the quality of the reconstructed image in the GI system.

On the other hand,orthogonal-triangular(QR)decomposition technique is a genuine contribution to the field of numerical analysis, where a rectangular matrix can be decomposed into orthogonal matrix and upper triangular matrix.[35]This technique can solve the eigenvalue problem in a very satisfactory way,and reduce the time for standard eigenvalue computations to the time required for a few matrix multiplies.[36–38]Therefore, inspired by the concepts of QR decomposition technique, we propose a novel ghost imaging scheme based on QR decomposition for the case where it is impossible to obtain the orthogonal measurement matrix,named QR decomposition ghost imaging (QRGI). In general, a matrix performed by QR decomposition must satisfy one of the following conditions, and the matrix is square or with full rank. Hence, in the scheme,we construct the new measurement matrix by performing QR decomposition in two circumstances. (1) When the measurement matrix is square,it can be first decomposed into an orthogonal matrixQand an upper triangular matrixR.Then let the off-diagonal values ofRequal to 0.0,the diagonal elements ofRequal to a constantk,wherekis the average of all values of the main diagonal,so the resulting measurement matrix can be achieved. (2)When the measurement matrix is with full rank,then its transpose should be first computed,and followed above QR operation. Finally,we can restore the image of the object by correlating the new measurement matrix and corresponding bucket values. Numerical simulations and experiments verify the feasibility of QRGI.

The remainder of the paper is arranged as follows. QRGI is presented in Section 2. In Section 3, the performance of QRGI is discussed by numerical simulations and practical experiments. Finally,the paper is concluded by Section 4.

2. Theory

Figure 1 shows the schematic diagram of the proposed QRGI scheme. Here, the whole imaging process of TGI system is regarded as a series of matrix operations.[32]In the system,the series of random illumination patternsI1,I2,...,INare generated by a projector and then projected onto the object successively,whereNis the number of speckle patterns. If the transmission coefficient of each illumination pattern is ap×pmatrix,the illumination pattern can be permutated into a 1×p2row vector. Then a new measurement matrix withNrow vectors andPcolumn vectors can be obtained,whereP=p×pis the number of pixels of the pattern. The measurement matrix is recorded as

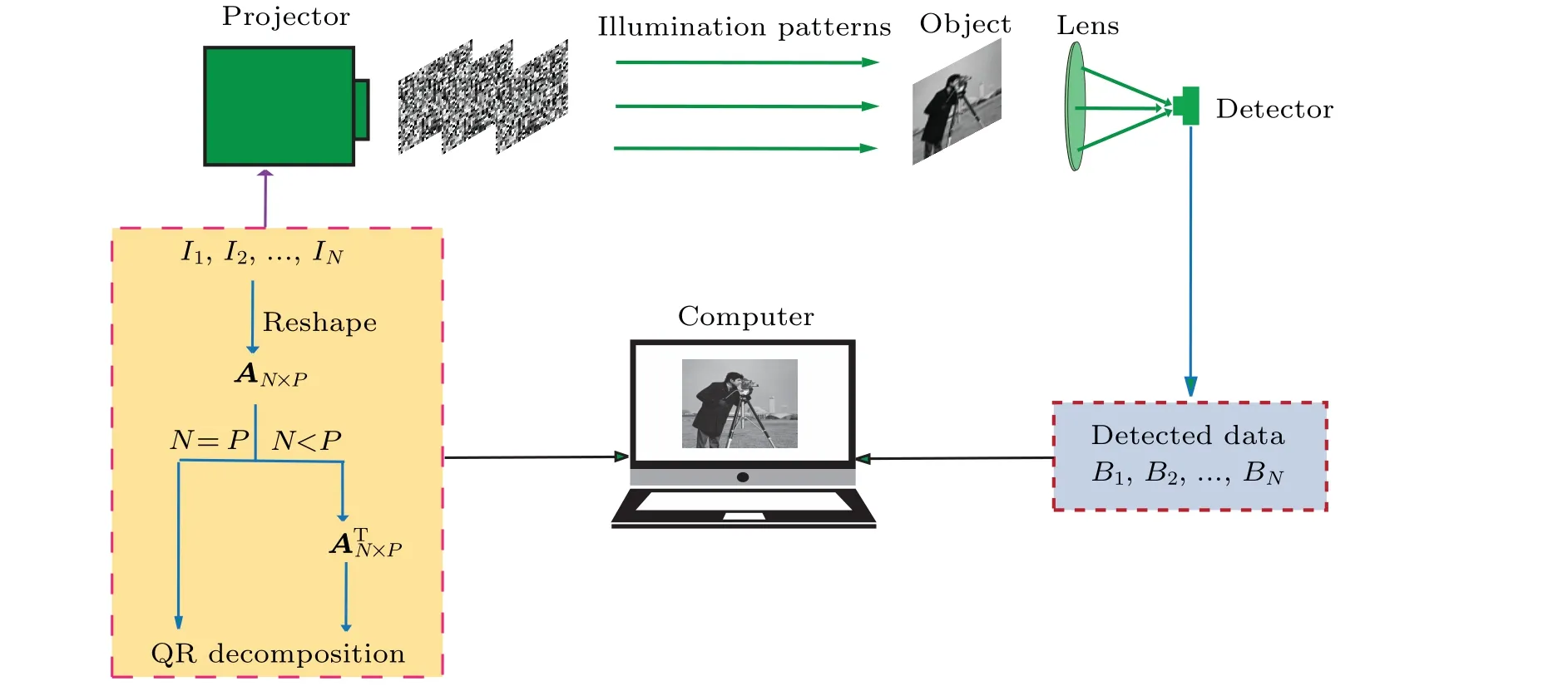
Fig.1. A schematic diagram of the QRGI scheme.

whereRTRis still an upper triangular matrix. Its diagonal elements represent the effective information for reconstruction.Therefore, we set the off-diagonal values ofRequal to 0.0,the diagonal elements ofRequal to a constantk, wherekis the average of all values of the main diagonal, andRTRin Eq. (8) can be replaced byk2E, whereErefers to an unit matrix. Hence,Eq.(8)can be approximate to

From Eq. (12) we can see that the closer theQQTis to unit matrix, the higher the quality of the reconstructed image is.Therefore, it is in principle that QRGI can get a restored image with a higher fidelity. Noted that the case ofN>Pis not considered since we have restored the object perfectly whenN=P.

3. Results and discussion

In this section,we will verify the proposed QRGI scheme by both numerical simulations and experiments. In order to demonstrate the quality of the reconstructed image, mean square error (MSE) is used as an objective evaluation,[40]which is defined as

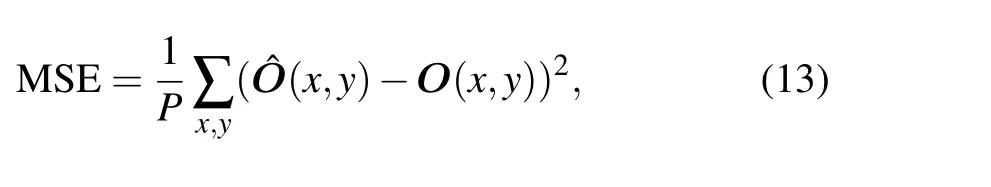
whereO(x,y)and ?O(x,y)refer to the original and the reconstructed object respectively,(x,y)is Cartesian coordinate,andPis the number of pixels of the image.

The experimental setup is shown in Fig.2,which includes a projector (DLP LightCrafter 4500), a photodetector (Thorlabs PMM02-1), a data acquisition card(National Instrument USB-6341), and a computer (Intel(R) Core(TM) i3-8145U CPU @ 2.10 GHz; RAM: 8.00 GB). As the bit depth of the projector is limited to 8, the quantization noise is introduced when the values of the random pattern are quantized. The speckle patterns,generated by the projector,are projected onto the target object. The photodetector,placed at the opposite of the object, is used to detect the light intensity reflecting from the object, and the data acquisition card (DAQ) is adopted to perform analogue-to-digital convert.Finally,the computer can reconstruct the object by correlating the speckle patterns and corresponding bucket values.

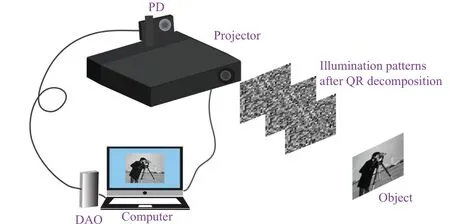
Fig.2. A schematic diagram of the QRGI scheme experimental system.PD:photodetector. DAQ:data acquisition card.

At first, we compute and display the products ofATAandATQRAQRto reflect which one is closer to unit matrix. We use a randomAof size 64×64 pixels, then constructAQRby our method. Later, we normalize the values ofATAandATQRAQRinto 0–255 grayscale,and graphically display them in Fig. 3, where the insets are the 2D grayscale images of the matrixes, andxandyrepresent the row and column coordinates of their elements,respectively. From the 2D matrix of Figs. 3(a) and 3(b), we can see thatATQRAQRis closer to unit matrix thanATAsince the off-diagonal values ofATAare much larger than those inATQRAQR. Besides, from the 3D maps of Figs. 3(a) and 3(b), we can see thatATAfluctuates violently, the diagonal elements are submerged by the off-diagonal values ofATA,while the off-diagonal values inATQRAQRare much clear,this also demonstrates thatATQRAQRis closer to unit matrix thanATA.Thus,QRGI is theoretically feasible.

Next,we testify the validity of QRGI by numerical simulations and experiments. In accordance with the experimental condition,we normalize the values of random speckle patterns into 0–255 grayscale in simulations,which will introduce the quantization noise. Choosing two pictures as the original objects, one is a grayscale image (‘Cameraman’) and the other one is a binary image(‘Star’). The results are shown in Fig.4,

where Fig. 4(a) are original images, Fig. 4(b) shows the reconstructed images with the size of 32×32 pixels,where the number of measurementsN=1024,and Fig.4(c)displays the reconstructed results with the size of 64×64 pixels, where the number of measurementsN=4096. The first two rows are simulated results, from which we can see that taking the Nyquist limit measurements(equal to the number of the image pixels), QRGI can perfectly reconstruct the object, while the images restored by TGI and DGI are more or less polluted by noise. Besides,taking the grayscale‘Cameraman’of 64×64 pixels for instance,there are two order of magnitude improvement in MSEs values in comparison with those of TGI and DGI. The last two experimental results also show that QRGI has a better performance than that of TGI and DGI. For both binary and grayscale objects,the imaging quality of the reconstructed images of QRGI scheme is better than that of TGI and DGI and corresponding MSEs are smaller, which shows that the proposed QRGI scheme has a better reconstruction performance.

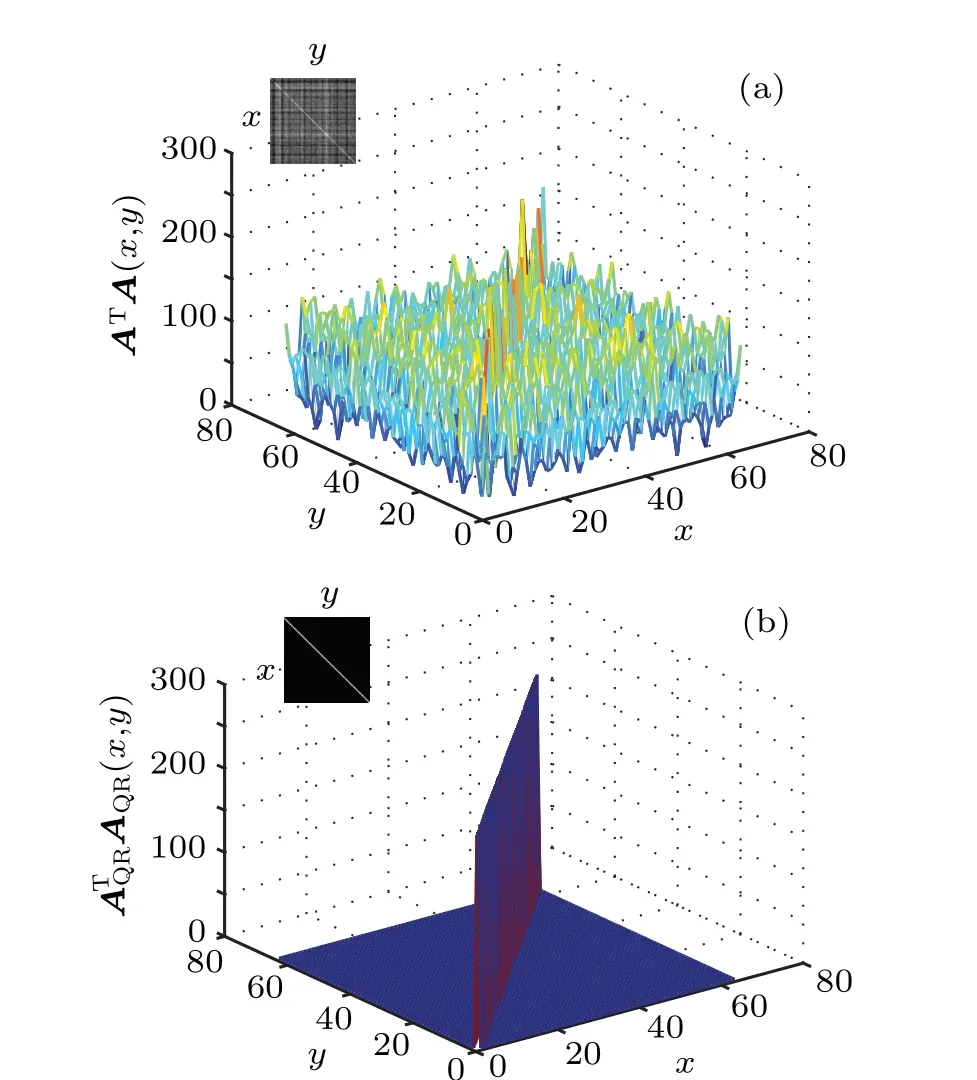
Fig.3. Comparison of ATA and ATQRAQR. (a)ATA,(b)ATQRAQR.Here x: row coordinates of the matrix; y: column coordinates of the matrix.

Figure 5 shows the MSEs curve against the different numbers of measurements by using TGI,DGI and QRGI schemes.Here the object is a binary ‘Star’ image with the size of 64×64 pixels, where Fig. 5(a) shows the simulated results,and Fig.5(b)shows the experimental results. The results indicate that as the number of measurements increases,the MSEs values decrease gradually for three methods, while the proposed QRGI scheme has a more rapidly rate. Compared with TGI and DGI, QRGI scheme could achieve better imaging quality at the same number of measurements.

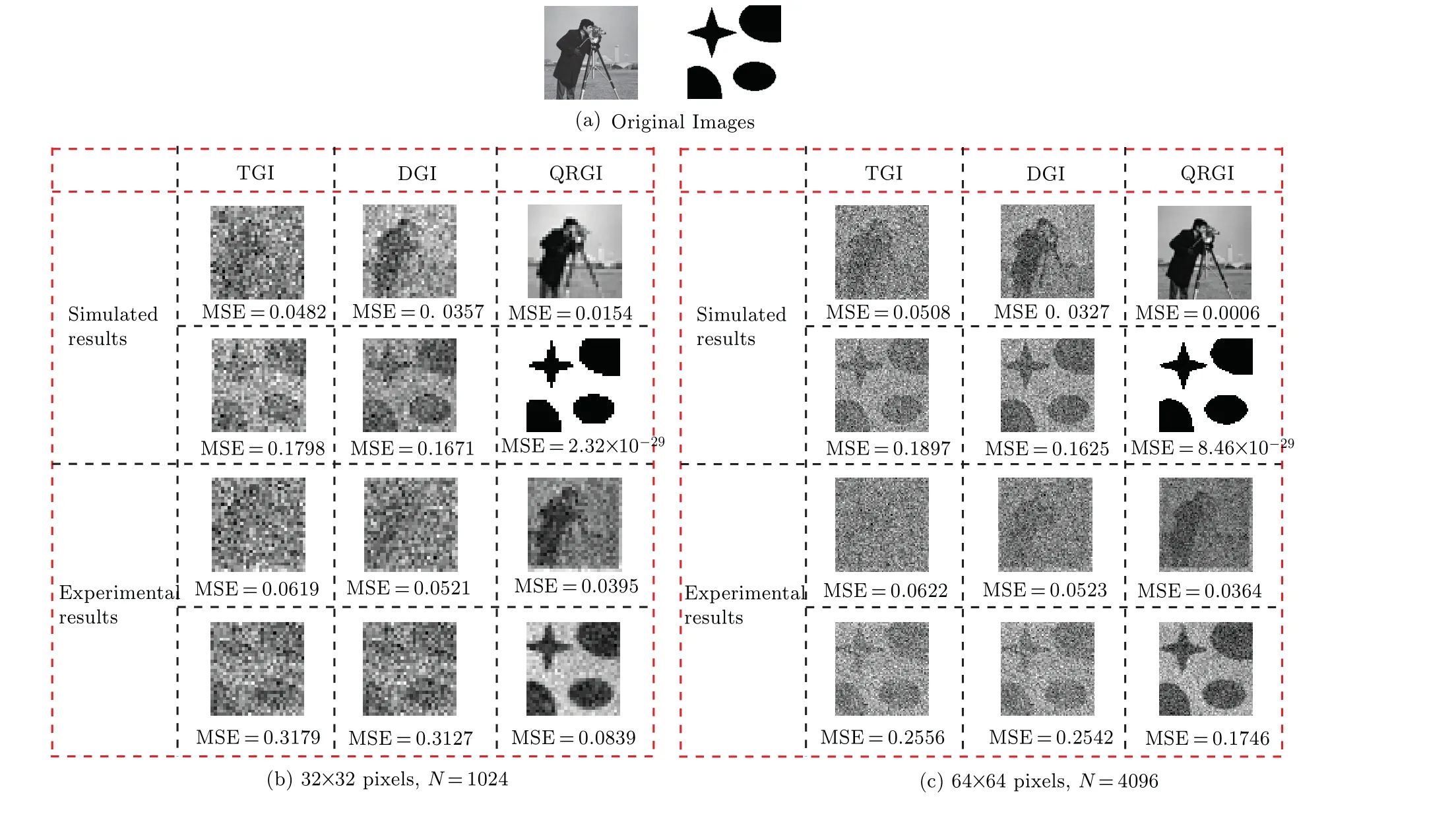
Fig.4. Simulated and experimental results comparison. (a)Original objects. (b)32×32 pixels,and N=1024. (c)64×64 pixels,and N=4096.

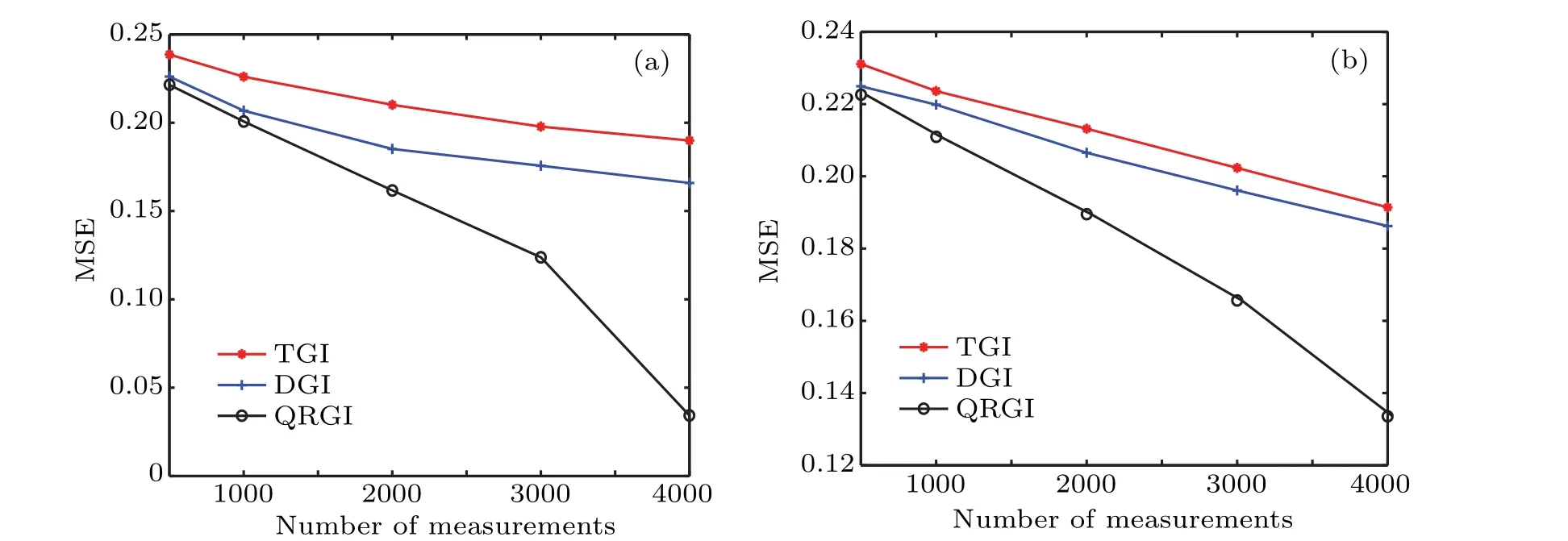
Fig.5.The MSEs curve against the different numbers of measurements by TGI,DGI and QRGI.(a)The simulated results.(b)The experimental results.

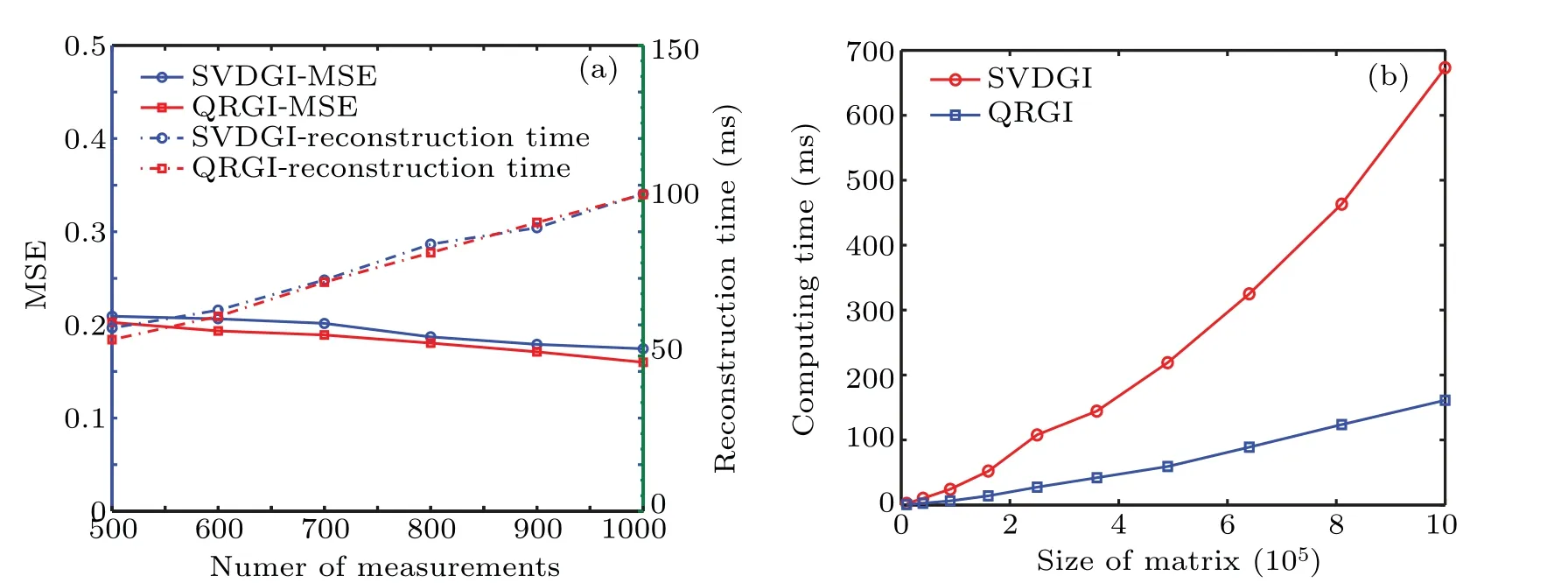
Fig. 6. Comparison by using QRGI scheme and SVDGI scheme. (a) The MSEs and reconstruction time curve against different numbers of measurements by using QRGI and SVDGI from experimental results.(b)The computing time curve against the size of the measurement matrix by using SVDGI and QRGI from simulated results.

Figure 6 further shows the MSEs and reconstruction time curve against different numbers of measurements by using QRGI and SVDGI from experimental results, together with the computing time (the time-consuming on the light patterns computation) curve against different numbers of measurements by QRGI and SVDGI from simulated results. Here,a binary ‘Star’ image with the size of 32×32 pixels is selected as the object in Fig. 6(a). The results show that the performance of QRGI and SVDGI are almost the same. Their MSEs values and reconstruction time are very closer at the same number of measurements, which indicates that QRGI can match the performance of SVDGI.Besides,a random rectangle matrix is selected as the measurement matrix to do QR decomposition and SVD transform in Fig. 6(b), from which we can see that with the increase of the size of the matrix,both schemes has a longer computing time, but the proposed scheme costs a less computing time. Therefore,the proposed QRGI scheme has a promising prospect in real applications.

4. Conclusion

In the paper,we have proposed a novel GI scheme to get a better imaging performance with QR decomposition,named QR decomposition ghost imaging, where the whole imaging process of GI system is regarded as a series of matrix operations. The numerical simulations and experimental results have shown that the reconstructed images by using QRGI have a better performance than those reconstructed by using TGI and DGI, and this improvement of imaging quality is without the consumption of physical dimensions of light field. In addition, the proposed QRGI scheme can match the performance of SVDGI,while the proposed QRGI scheme requires a shorter computing time. The proposed scheme is appropriate for the cases where it is impossible to obtain the orthogonal measurement matrix. We believe that the usage of QR decomposition developed in the field of numerical analysis to the GI system provides a way for new GI schemes.

Acknowledgements

Project supported by the National Natural Science Foundation of China (Grant Nos. 61871234 and 62001249), the Postgraduate Research & Practice Innovation Program of Jiangsu Province, China (Grant No. KYCX20 0729), Natural Science Research Project of Higher Education of Jiangsu Province, China (Grant No. 20KJB510030), and Research project of NanJing Tech University Pujiang Institute (Grant No.njpj2020-1-02).