Complex-Valued Neural Networks:A Comprehensive Survey
ChiYan Lee, Hideyuki Hasegawa,, and Shangce Gao, Senior
Abstract—Complex-valued neural networks (CVNNs) have shown their excellent efficiency compared to their real counterparts in speech enhancement, image and signal processing.Researchers throughout the years have made many efforts to improve the learning algorithms and activation functions of CVNNs. Since CVNNs have proven to have better performance in handling the naturally complex-valued data and signals, this area of study will grow and expect the arrival of some effective improvements in the future. Therefore, there exists an obvious reason to provide a comprehensive survey paper that systematically collects and categorizes the advancement of CVNNs. In this paper, we discuss and summarize the recent advances based on their learning algorithms, activation functions, which is the most challenging part of building a CVNN, and applications. Besides,we outline the structure and applications of complex-valued convolutional, residual and recurrent neural networks. Finally,we also present some challenges and future research directions to facilitate the exploration of the ability of CVNNs.
I. INTRODUCTION
GENERALLY, real-valued neural network (RVNN) is the widely applied neural network with all its parameters,input and output values being in real numbers. CVNNs, on the other hand, gain less attention than RVNNs, have complex numbers as their inputs and network parameters. The outputs of CVNNs are either in real or complex numbers based on the interest of study. Real numbers are frequently applied due to their less computational complexity and easier implementation compared to complex numbers. The idea of CVNNs was started when a researcher included phase information in the computation of his invention called “Parametron”. It is further studied and a comprehensive design of CVNNs is proposed by[1], [2], where the network parameters and the most commonly used back-propagation (BP) algorithm are extended into complex domain [3]. Their proposal eases the processing of the wave-typed signal easier, especially electromagnetic and sonar signals. Recently, the applications of CVNNs have become wider in the field of MRI signal processing [4],speech enhancement [5], wind prediction [6], image classification and segmentation [7], [8].
CVNNs are the most compatible model for wave-related information processing as it can directly deal with the phase and amplitude components. In the wave signal, phase components represent the time course or position difference,whereas amplitude denotes the energy or power of the wave[9]. Hence, wave information can be fully extracted when training it with CVNNs rather than RVNNs [10]. Moreover,the phase rotation and amplitude attenuation feature embedded in complex numbers reduce the degree of freedom in the neural network.
Furthermore, studies have also proven that CVNNs have a less effect on the existence of singular points than RVNNs during neural network training since the updating mechanism of the complex-valued back-propagation (CBP) algorithm increases the speed of moving away from the singular points[11]. However, the design of a complex-valued activation function conforms to Liouville’s theorem, where it makes the direct extension of the real-valued activation function into complex domain difficult.
In the literature, [9], [12], [13] discussed the merits of CVNNs by explaining the mathematical expression of complex numbers and relating it to the signal processing field.However, these papers did not discuss the learning algorithm of CVNNs and focused on a particular type of application only. Furthermore, a book that covers the construction,applications and advantages of CVNNs has been published in 2012 [10]. Also, a recent survey paper on CVNNs [14],includes the learning algorithms, applications and future research directions of CVNNs has been published in 2021.Although the book and this survey paper present a good fundamental knowledge of CVNNs, there are significant differences between our study and [10], [14], summarized as:
1) References [10] and [14] did not present the variants of CVNNs, such as complex-valued CNN, complex-valued RNNs and complex-valued residual neural network, while we introduce the variants of CVNNs by discussing their structures and advantages;
2) Reference [14] did not critically summarize the applications of CVNNs, while we highlight the strength and weakness of the applications to make it easy for the researcher in improving their studies;
3) In the future research directions of CVNNs, we emphasize and suggest the potential of CVNNs in representing biological neurons by discussing the use of complex numbers in spiking neural networks, which is one of the active research topics in neural network community.
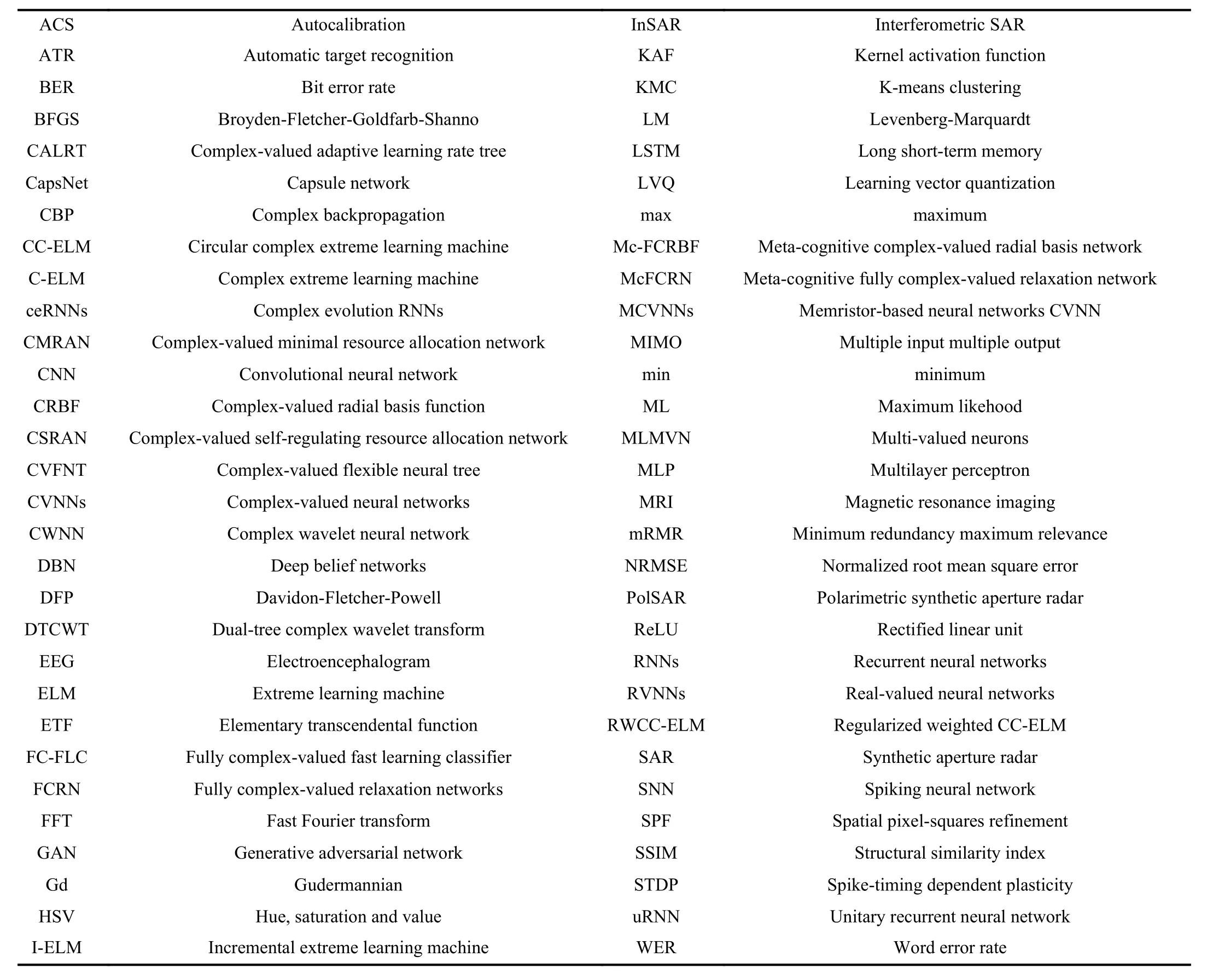
TABLE I A LIST OF ABBREVIATIONS IN THIS PAPER
Accordingly, our study aims to give the following main contributions:
1) A comprehensive collection of variants of CVNNs up to year 2021 is presented with the aim to provide insights into the fundamental structure of different kinds of CVNNs.
2) A systematic categorization of the recent applications of CVNNs in various fields by summarizing the strength and weakness of their studies provides an easy reference for the researchers in neural networks community.
3) Future research prospective on CVNNs is discussed.
Also, the use of complex numbers in network training is often questioned. To address that, our paper highlights the advantages and biological motivation of CVNNs to attract the attention of researchers in the neural network field in investigating some effective approaches of CVNNs. Table I gives a list of abbreviations in this paper. Fig. 1 describes the hierarchically-structured taxonomy of this survey.
The rest of this paper is organized as follows: Section II discusses the motivation of CVNNs. Section III describes the types of CVNNs while Section IV summarizes the learning algorithms and activation functions of CVNNs. Section V discusses the variants of CVNNs. Section VI explores the application of CVNNs in this decade. It is followed by a discussion on the challenges and future research directions of CVNNs in Section VII. Finally, we draw a conclusion in Section VIII.
II. MOTIVATION OF CVNNS
Why are CVNNs needed? The question always arises with the necessity of including complex numbers in neural network training since the real number has gained great success in various applications. In this section, we attempt to provide the answer to this question. Complex numbers have always been considered as a mathematical abstract that does not exist in the real world. Nevertheless, we strongly emphasize that complex numbers exist by stating some practical examples. Complex numbers exist in the radar signal, where the images of Earth’s surface are collected using InSAR for ground deformation mapping purposes. Such radar images are composed of ground’s physical properties information and the distance,represented by the amplitude and phase difference respectively in complex number [15]. In addition, complexvalued signal can be found inherently in electromagnetic and MRI signal [4]. Virtueet al. [4] report that CVNNs are more accurate than RVNNs in the inverse mapping of MRI fingerprinting. This leads to the use of complex numbers in real-world applications.
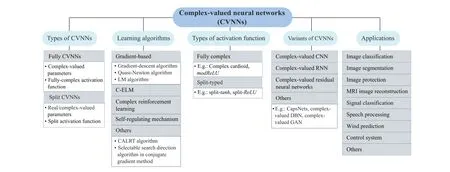
Fig. 1. Hierarchically-structured taxonomy of this survey.

RVNNs are undeniably exhibiting extraordinary performance in deep learning eras, yet, the ability of a single realvalued neuron is still limited. A typical example is the XOR problem which a single real-valued neuron cannot solve.However, a single complex-valued neuron can solve such problem with high generalization ability, where Nitta [18]reports the concept of orthogonal decision boundary exists in the complex-valued neuron. Two hypersurfaces intersect orthogonally and divide the decision boundary into four regions. With the orthogonal property, his study also solves the detection symmetry problem and reveals the potential computational power of CVNNs.
Furthermore, the neural network configuration is said to represent the neuronal communication mechanism in the human brain. However, despite the success of neural networks lately, the process of neuronal information communication is not yet fully manifested in the current neural networks, neither in RVNNs nor CVNNs. In 2014, a related study [19] proposes a biologically plausible neuronal formulation that allows us to construct a richer, versatile deep network representation in CVNNs. Generally, neurons convey information in the form of rhythmic electric action potential (i.e., spikes). Such rhythmical spikes are characterized by their average firing rate and the relative timing of the activity, which is represented by the amplitude and phase in complex numbers. RVNNs, on the other hand, represent the neuron’s output as a scalar real number, which can be interpreted as the average firing rate of the neuron. In their study, experiments on deep Boltzmann machines are performed to assess the synchronization of the rhythmic neuronal spikes (i.e., to assess the importance of phase). Inputs with similar phases are called synchronous as they sum constructively, while different phases are asynchronous. Their finding shows that the phase of the resulting complex-valued inputs influences the phase of the output neuron. This demonstrates the effect of synchronous neuronal firing on a postsynaptic neuron and proves the importance of the phase in neuronal communication.
With the potential computational ability of CVNNs and the supportive evidence from the biological perspective, we believe it is reasonable to apply complex numbers to neural networks.
CVNNs are first started as split-CVNNs, where the complex-valued input (real and imaginary parts) splits into a pair of real-valued inputs and feeds into the RVNNs. The input value splits in a fashion of either rectangular (real and imaginary) or polar coordinates (phase and magnitude), as shown in (1) and (2), respectively.
III. TYPES OF CVNNS
Split-CVNNs are divide into two categories: split-CVNNs with both real-valued weights and real-valued activation function, and split-CVNNs with complex-valued weights and real-valued activation function. However, the former increases the input dimension, learnable parameter and, subsequently,enlarges the network size. On top of that, it leads to phase distortion and inaccuracy in approximating the output of the neural network as it is updated by using real-valued gradients,which does not represent the true complex gradient [20]. In[21] and [22], sensitivity analysis and convergence study are performed in split-CVNNs with both real-valued weights and real-valued activation function and proved that the neural network convergence strongly depends on proper initialization and the choice of learning rate [20]. On the other hand,CVNNs with complex-valued weights and real-valued activation function [1] overcome the phase distortion problem,which is caused by the splitting of complex-valued signal into two real-valued components. It is widely applied in [23]–[26]as it is easier to compute with the use of real-valued activation function, for example, rectified linear unit (ReLU), sigmoid and tanh function as shown in Section IV-B.
To deal with complex-valued signals, fully CVNNs have been proposed by [27] where both of the weights and activation functions are in the complex domain. Fully CVNNs preserve the information carried by phase components. Hence,they are widely applied in medical MRI image reconstruction[28], SAR image interpretation [29] and telecommunication(especially for the channel equalization) [20], [30], [31].However, fully CVNNs increase the computation complexity and face difficulty in obtaining complex-differentiable (or holomorphic) activation function [2]. Examples of fully complex activation functions are shown in Table II.
IV. LEARNING ALGORITHM AND ACTIVATION FUNCTION
A. Learning Algorithm and Mechanism
Some learning algorithms that have been applied in CVNNs are discussed in this section.
1) Gradient-Based Algorithm:BP algorithm, the most common learning algorithm of neural network is extended into complex domain by [1]–[3], [42], [43]. It is difficult to extend the real-valued BP into CBP due to the complex differentiability of the activation functions in CVNNs. Generally, the activation function in RVNNs is entire and bounded.However, both of these properties are undesirable in the complex plane, since the Liouville’s theorem states that bounded and entire function is constant. Therefore, most of the activation functions are designed with bounded but compromising the entire properties.
Although CBP is popular in neural network training, it is often trapped in the local minimum and has slow convergence.Hence, some efforts in improving the CBP algorithm have been performed throughout the years, for instance,combination of CBP with global optimization algorithm [44],adaptation of genetic algorithm for the weight initialization[45], implementation of hybrid incremental algorithm into CBP [46], and gradient regularization improvement in CVNNs [47]. Recently, a novel learning algorithm is proposed, where the output weights are iteratively determined by the trained input weights in the complex domain [48].Hence, there exists a strong nonlinear relationship between the input and output weights. As compared to the conventional BP-based algorithm, their study reduces the number of iteration required to achieve the same training error.
A widely used minimization criterion in CBP is shown in(3). The error function,Edoes not fully represent the amplitude and phase in complex numbers.

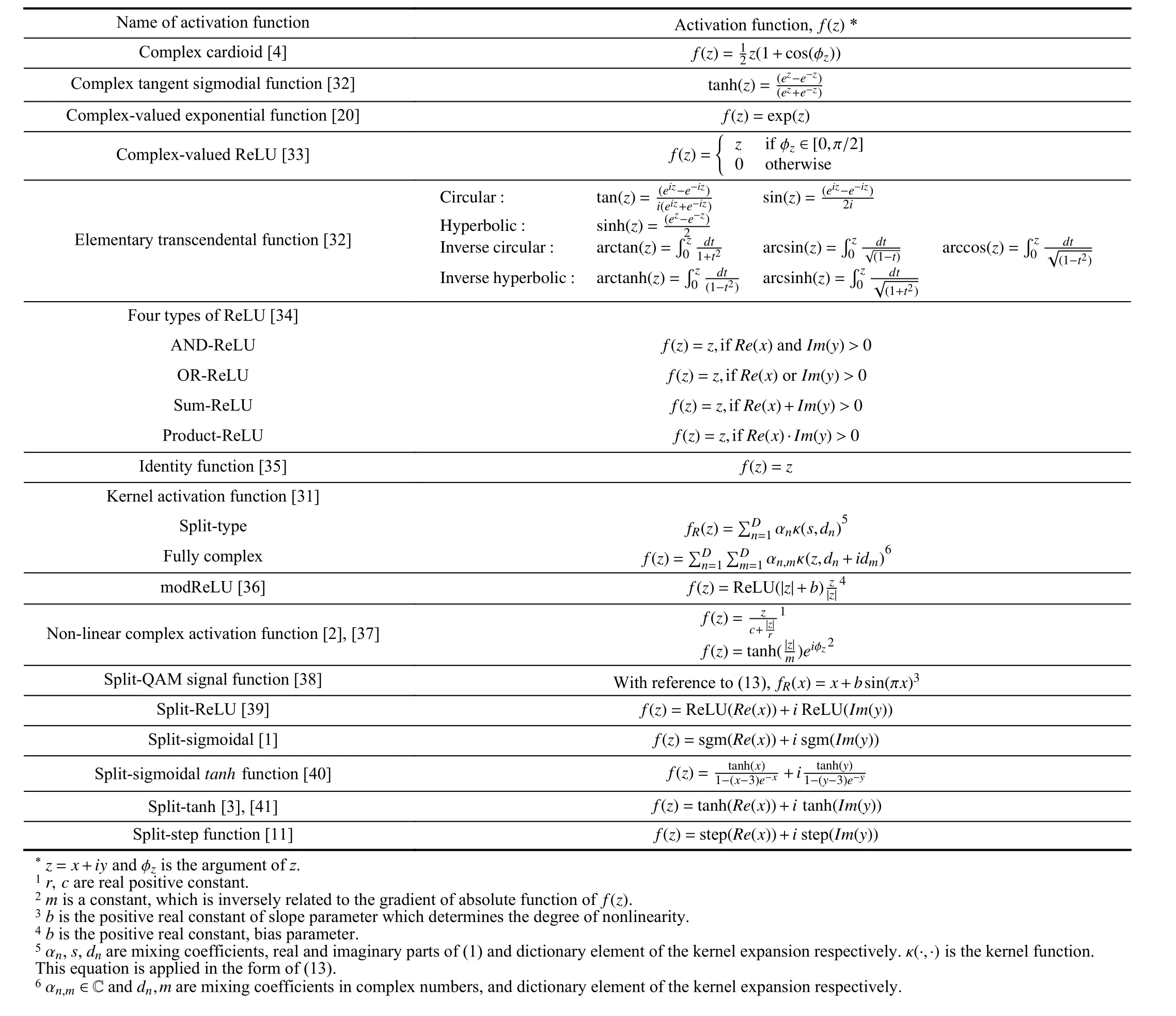
TABLE II SUMMARY OF SPLIT AND FULLY COMPLEx ACTIVATION FUNCTIONS THAT APPLIED IN CVNNS

Batch mode, online mode and mini-batch mode are three different training modes of the BP algorithm [51]. Batch mode is commonly applied in the training where it accumulates the weight correction over the entire training samples before the weight updates. In the online mode, the weight is updated immediately after feeding the training samples. On the other hand, mini-batch mode combines these two approaches, where the gradient is computed over a block of samples and the weight is updated after presenting all samples. As the minibatch mode is proved to have better generalization ability and higher learning speed [52], it is extended into the complex domain for the training of CVNNs [53]. In addition, the introduction of the new Taylor mean value theorem for analytic equations allows one to perform the convergence analysis of the proposed algorithm. Their study shows that the fully complex mini-batch algorithm outperforms its realvalued counterpart in terms of convergence rate.
Moreover, quasi-Newton learning algorithm is also a kind of gradient descent method, where the computation involves second order derivatives. The work in [54] extends the quasi-Newton method into the complex domain with three different inverse Hessian approximation approaches, which are the BFGS, DFP, and symmetric rank-one method. This study exhibits a full deduction of the quasi-Newton method in CVNNs and the performance is evaluated and compared with the conventional CBP algorithm. The quasi-Newton method results in a higher rate of convergence and, thus, provides faster optimization. Followed by that, a convergence theorem is proposed to stipulate that the weights generated by this approach can converge towards the minimal point of the cost function [55].
LM algorithm, on the other hand, is a damped least squared method that minimizes the sum of squared error between a set of data points and the function [56]. It combines the ideas of gradient descent algorithm and Gauss-Newton method by adding a damping parameter into their network update equation, where the extremely small value (approximate to 0)of damping parameter results in Gauss-Newton method, while large value results in gradient descent method. LM algorithm is extended into the complex domain based on Wirtinger calculus [8], [57]. A complex version of LM algorithm exhibits higher accuracy and convergence rate than the CBP algorithm. However, it requires vast memory to store Jacobian matrices when dealing with massive data.
2) C-ELM:ELM is a single-layered feed-forward neural network that requires no parameter tuning as the conventional gradient descent algorithm. The weight and bias in the input layer are obtained randomly and the output weight matrix is computed analytically. It has gained attention in the real domain as its ability to avoid local minima trapping, shorter time taken for training, and exhibiting better generalization ability. It is noteworthy that ELM can be applied to any activation function, no matter it is differentiable. With that,ELM has been extended to the complex domain by [30] and its performance is superior to all the previously available algorithms, including CBP, CRBF and CMRAN. Followed by that, the I-ELM is also proposed where the randomly generated hidden nodes are added incrementally and the output weight matrix is determined analytically [58]. It also shows the ability of I-ELM as a universal approximator, only if the bounded non-linear piecewise continuous activation function is applied.
After the idea of C-ELM is proposed, some researchers incorporate other elements into it to enhance its performance.First, in dealing with real-valued classification problems, a non-linear transformation with translational/rotational bias term is used at the input layer to perform the one-to-one mapping from real-valued to complex-valued feature space[59]. The proposed transformation is known as CC-ELM and its transformation function is shown as follows:
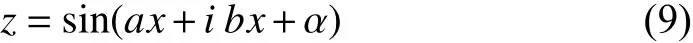
whereαdenotes the non-zero translational/rotational bias term,aandbare real-valued non-zero transformation constants.
Second, FC-FLC adopts the features in CC-ELM for their input weight generation and output weight estimation [60].Their proposed model formulates twoGdactivation functions where they are continuously differentiable and the magnitude response plot follows the inverse Gaussian function characteristics. These indicate thatGdcan be a good discriminator.
Followed by the proposal of CC-ELM, the work in [61]combines it with weighted ELM [62] and the hybrid model is known as RWCC-ELM. The weighted ELM is a variant of ELM, which calculates the optimal weights between hidden and output layers by minimizing the weighted least square error function. This hybrid model is used to handle the class imbalance problem, where it assigns the minority class with more weight. It contributes significantly to weighted least square error and reduces the misclassification of minority class samples.
3) Complex-Valued Reinforcement Learning:Reinforcement learning is prevalent in training the neural network to learn the best possible action for attaining a particular goal[63], [64]. Generally, an agent observes its state, selects an action for the particular state and propagates to the next state.A reward is given to the agent based on the next states. The agent learns continuously and maximizes the cumulative reward. By extending it into a complex domain, it eases the expression of state-action pairs in time series. However, the complex domain extension does not gain much attention among the researchers within these ten years and the number of published papers is less than its real counterpart.
In 2006, a complex-valued reinforcement learning algorithm is proposed by extending some conventional algorithms in real-valued cases, for instance, Q-learning and profit sharing[65], [66]. With this extension, Shibuyaet al. [67] propose CRBF networks using the complex-valued reinforcement learning algorithm (Q-learning). Their work is then compared by Mochidaet al. [68], who applies the algorithm into CVNNs. In the latter work, Shibuyaet al. express both the action value functions into a single network, where both of these values are represented as multiple networks (the real and imaginary parts are treated independently) [67]. Such input values expression significantly reduces the number of network parameters, which also lowers the memory size.

4) Self-Regulated Learning Mechanism:Compared to the preset learning algorithm [69], a neural network that can decide its learning pattern within the meta-cognitive environment is proposed. Inspired by the principles of the human learning mechanism, the proposed model is claimed as the best learning strategy. To extend it into the complex domain, Savithaet al. [70] successfully develop Mc-FCRBF.Motivated by [70], CSRAN [71] is proposed with extended Kalman filter instead of gradient descent algorithm in updating the network parameters. Moreover, the number of hidden neurons in CSRAN is not fixed a priori, but it is fixed in Mc-FCRBF. The hidden neurons are built up or pruned by the magnitude and phase error criterion. On the other hand,both of these networks consist of self-regulatory schemes,which allows them to control the learning process by performing sample deletion (what-to-learn), sample learning(how-to-learn) and sample reserve (when-to-learn).
McFCRN is proposed with a similar self-regulating mechanism. Its primary difference with the CSRAN and Mc-FCRBF is the error function computing approach, where McFCRN applies logarithmic error function. It explicitly represents the magnitude and phase of complex-valued error as the energy function. Together with the projection-based learning algorithm in this network, optimal weight is calculated corresponding to the minimum energy point of the energy function [72]. The returning of the system back to minimum energy states from its initial condition is similar to the relaxation process, where the neural network is named after [73]. Adding meta-cognitive components (i.e., selfregulating scheme) into FCRN successfully improves its approximation and classification ability.
5) Others:Other than the self-regulating mechanism discussed above, the CALRT algorithm is proposed to efficiently determine the complex-valued stepsize (or learning rate) of CVNN during each iteration of training [74]. It enables the neural networks to search for the optimal complex-valued learning rate in each particular iteration via searching it in a tree-like manner. The rotation factor identifies the search direction, while the scaling factor identifies the learning amplitude along that direction. Hence, by adjusting the factors in CALRT, the optimal search range can be found and provides a better search direction in each iteration. In addition, escaping from saddle points is always a challenging problem in training neural networks. CALRT algorithm is flexible in searching the learning rate in each iteration and makes the training algorithm escape from saddle points easily. Having the flexibility to update the learning rate adaptively is advantageous; however, it is time-consuming when the search range becomes large, and overfitting issue occurs when the number of iterations is too large. Inspired by the real-valued version of the CALRT algorithm, Donget al.[75] propose a selectable search direction algorithm in the conjugate gradient method for CVNNs. It possesses a similar tree-like search structure in [76] that increases the flexibility of the searching direction for the direction factor in the conjugate gradient method.
B. Activation Function
One of the most challenging parts in CVNN is to design a suitable activation function for CVNNs as Liouville’s theorem states that a complex-valued function which is bounded and analytic everywhere (i.e., a function that is differentiable at every pointz∈C), is constant. In other words, a function that is bounded and analytic everywhere in the complex plane is not a suitable CVNNs activation function. Therefore, most of the activation functions in CVNNs are designed by selecting one property (i.e., boundedness or analytic). The activation functions in CVNNs can be divided into two categories. First,split activation function, where real and imaginary parts are treated independently, as shown in (13). Second, fully complex activation function, where real and imaginary parts are treated as a single entity. Most of the activation functions in CVNNs are adopted directly from its real-valued counterpart, which is bounded, except for the ReLU function.A summary of split and fully activation functions is tabulated in Table II.
1) Split Activation Function:Initial idea of split activation function is proposed by [1], [3], [41], where they adopt the real-valued activation function (for example, tanh and sigmoid function) as shown in (13). Such activation function is bounded and not analytic [1]achieve the minimum validation error) [25].

Split activation function with complex-valued output neurons:The conversion of complex-valued output into the real domain does not fully represent the output of CVNNs since the real number is interpreted as the magnitude component only while ignoring the phase component. Thus,such conversion is not favorable where the phase component also carries important information.
In addition, some of the literatures highlight the effectiveness of applying adaptive activation function in RVNNs[77], where they allow the network to adapt its shape based on the training data, improving the network’s accuracy. For instance, Scarpinitiet al. [78] apply the adaptive bi-dimensional activation function in CVNNs to process complex communication signals. It is a bounded and locally analytic function composed of a flexible surface, which can adaptively modify the corresponding learning process. Moreover, the work in [31] proposes a non-parametric activation function,KAF, which can be represented in terms of split and fully complex activation function.

Among all the ETFs, a rcsin(z) and arcsinh(z) show the best average convergence rate (i.e., the ability to achieve the preset mean squared error (MSE) within 10 000 training samples).These functions are analytic, removable singularity and possess consistent circular contour amplitude response. They tend to escape from the nondiscriminating flat portion of the sigmoidal function. Savithaet al. [20] propose an exponential activation function and evaluate its performance with the selected ETFs (i.e., all the ETFs are performed convergence analysis before the study and two ETFs with good convergence characteristics are selected), arcsinh(z) and arctan(z).Even if the ETFs are derived from exponential function, they exhibit lower generalization ability and convergence rate, and this may be caused by the presence of singular point in ETFs.
3) Performance of Split and Fully Complex Activation Function:CVNN can be applied for solving both real-valued and complex-valued problems but the performance of activation function varies with respect to the type of dataset.In solving real-valued problems, the most popular classification dataset, CIFAR-10, CIFAR-100 and MNIST databases are used to evaluate the performance of activation function in [31]. In [80] and [81], split-ReLU outperforms all other activation functions, namely, split-tanh, identity function, modReLU, complex-valued ReLU, complex absolute magnitude ((14)) and its squared ((15)) in terms of convergence rate and classification error.
Split activation function possesses superior performance in dealing with real-valued classification problems as its configuration is similar to the RVNNs. In the study of [80],they suggest the CVNNs should be applied to the real-valued classification problem in the following conditions, when:
i) Noise in input data is distributed on the complex plane.
ii) Input data can be naturally mapped into complex number.
iii) Complex-valued embedding can be learned from realvalued input data.
Additionally, the real-world dataset of wind prediction task[82] is also used to evaluate the performance of the activation function. Scardapaneet al. [31] compare the performance among split-tanh, split-ReLU, non-linear complex activation function, complex-valued ReLU, modReLU, and KAF. The proposed split-KAF significantly outperforms the others. On the other hand, Tachibana and Otsuka [34] propose four types of complex-valued ReLU and compare their performance with split-ReLU in wind prediction task by using the dataset in[83]. The experimental result shows that AND-ReLU and ORReLU outperform the other ReLU in wind prediction for 12 hours and 6 hours ahead, respectively.
Comparison of performance among activation functions in dealing with complex-valued input signals is also studied in MRI fingerprinting [4] and channel identification task [31]. In the study of [4], they compare between the proposed complex cardioid function with split-sigmoid and non-linear complex activation function in identifying tissue parameters from the MRI signals. Their proposed complex cardioid function preserves the phase components but attenuates the amplitude of the complex-valued signal. Therefore, the proposed function can outperform the other activation functions. On the other hand, the split-KAF shows superior performance in channel identification. The choice of activation function is essential in training a model for better prediction and classification performance. Hence, the properties of input data should be studied in terms of linearity and the desired information (phase or magnitude) before selecting an activation function.
V. VARIANTS OF CVNNS
In this section, variants of CVNNs are summarized and discussed detailedly. Table III lists some representative publications for each variant of CVNN.
A. Complex-Valued CNN
Real-valued CNN was first proposed in 1990 for handwritten digit recognition [84] and it has been widely applied in computer vision [85], time series prediction [86], autonomous vehicle [87], image recognition and classification task [88].Feature extraction and classification are the two essential working parts of CNN. It allows the successive layers in CNN to learn, discover the underlying features and classify them in the last fully connected output layer. Due to its outstanding classification performance, CNN has extended into complex domain, which enables the accurate representation of input data (magnitude and phase) [89]. Furthermore, complexvalued weights are more stable and numerically efficient in the memory access model [90]. Basic layers that are presentedin complex-valued CNN are discussed in detail as follows:
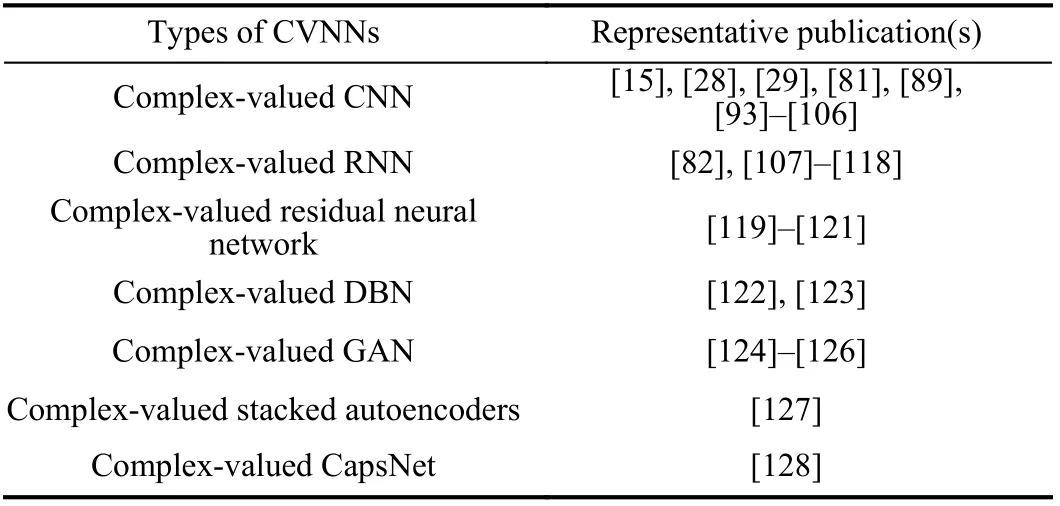
TABLE III VARIANTS OF CVNNS
1) Convolutional Layer:Each neuron in CNN is arranged in the feature map and connected to the filter banks or kernels in the convolutional layer, which consists of weight matrices in the complex domain. The kernels move through the feature maps, where the unit in feature maps is convoluted with weight matrices in the kernels. Then, the convoluted result is fed into an activation function to compute a new feature map[91].
The convolutional layer can be served as a feature extractor because each filter bank captures specific regional features in the input data. It detects the edge, color, gradient orientation of the image, which provides the model a comprehensive understanding of input images. Moreover, feature maps in the same channel always share the same filter bank due to the fact of spatially correlated image data [92], where the important feature in an image is usually fixed on one part. Thus, moving the same filter bank to capture the feature in the different parts of an image is necessary.

2) Pooling Layer:The pooling layer is sometimes placed after the convolutional layer in CNN. It functions to summarize the presence of features in patches of feature maps after convolution operation. Hence, it is also known as the downsampling layer, where it reduces the dimension of the feature map and produces a lower resolution version of the input signal. Also, it helps to exclude some unnecessary details in the input signals [129]. The two most common pooling computations are the maximum and the average of a filter size neighborhood in the feature map, known as maxpooling and average pooling, respectively.

B. Complex-Valued RNNs
RNNs, also known as auto-associative or feedback networks, are extensively applied in processing time series and sequential information. One of the most common architectures of RNN is LSTM, where the long-term dependencies can be learned to predict the output based on the given historical input data. In the literature of past decades, there has been many studies in the development and application of realvalued RNNs [131], [132]. On the other hand, complexvalued representation of RNNs has gained some attention in the deep learning community when it is proved to have enhanced learning stability in [107]–[111]. The basic definition of RNN is shown as

Most of the complex-valued RNNs studies have focused on stability, convergence analysis, and architecture enhancement in the recent ten years. There are only a few published articles regarding its application. For instance, complex-valued RNNs have been applied in wind power and profile prediction [82],[112], music information retrieval system [113], [114], automatic speech recognition [115] and channel equalization[116].
Problems and Enhancements in Complex-Valued RNNs:
Training and optimization of RNNs are challenging since they are prone to vanishing and exploding gradients during the learning process of long-term dependencies. These issues can be circumvented by gradient clipping, gating [133], and normpreserving state transition matrices [36]. In the study of [36],uRNN incorporates the unitary weight matrix,Uin its hidden layer, which is a complex-valued, norm-preserving state transition matrix in the conventional RNNs. It preserves the gradients over time and subsequently prevents both vanishing and exploding gradient problems. However, to enable computational efficiency, the weights are constructed as a product of component unitary matrices. Such construction causes them to span merely part of the unitary matrices and does not express the full set. Thus, a few alternatives to parameterize the unitary matrices have been proposed [118],[134] to achieve better performance.
In the study of [134], the span of unitary space is increased,where it can be tuned correspondingly to the task and achieves optimal performance of RNNs structure. Moreover, a full capacity RNN [118] is also proposed by using stochastic gradient descent for training the unitary matrices. This approach achieves equivalent or superior performance to the restricted-capacity type uRNN and LSTM, which requires gradient clipping during optimization. Hence, this indicates the importance of spanning in unitary space for application in RNNs. Furthermore, complex-valued gating is also proposed and inserted into uRNN [135]. It successfully facilitates the learning of longer-term temporal relationships and shows excellent stability and convergence during training.
Meanwhile, the unitary property in the approach mentioned earlier is questioned and studied by [115], in which they propose a ceRNNs that drops the use of unitary diagonal matrix in the computation. The proposed structure is evaluated in the multivariate regression model, copying memory problems and a real-world task, automatic speech recognition.It outperforms the uRNN in the multivariate regression model and has the identical performance as uRNN in copying memory problems, which indicates that the unitary constraint is not necessary to retain memory. In dealing with automatic speech recognition, both uRNN and ceRNNs are inferior to the conventional LSTM method due to the absence of gating mechanism in their structure. With the incorporation of LSTM into ceRNNs, the model improves WER, demonstrates that the unitary property in the diagonal matrices can be omitted depending on the tasks.
However, a study in [111] exhibits that the performance of complex-valued RNNs does not outperform its real-valued counterpart. The proposed network is evaluated with synthetic wide-band frequency datasets and the final test error of realvalued RNNs is lower than that of complex-valued RNNs.The poor performance shown in this study may be due to the inappropriate choice of activation function; hence, a comprehensive investigation of activation function suitability should be performed in the future. Despite the poor performance of complex-valued RNNs, they found that complex-valued RNNs can learn the domain of the dataset by observing the first three filter layers. In short, this study exhibits the importance of appropriate activation function and the learning ability of CVNNs in magnitude and phase-encoded datasets.
Other than that, researchers are encouraged to divulge the possibility of incorporating convolutional and recurrent neural networks in the complex domain. The hybrid model has shown some improved performance in dealing with the realworld task, for instance, activity recognition by a multimodal sensor in wearable device [117], remaining useful life prediction of machine [136], and handwritten music recognition[137].
C. Complex-Valued Residual Neural Network
Residual learning, proposed by [138], inserts shortcut connections into a standard CNN to reduce the network degradation problem, especially in deep networks. Such reformulation provides a shortcut path for gradient flow from lower network layers and avoids the vanishing gradient problem in backpropagation. With its excellent performance in image recognition, it is extended into complex-valued version to tackle the complex-valued signals, such as MRI signals [119]. Also, the residual learning layer is inserted in deep learning-based compressive sensing methods for image reconstruction [120].
In addition, treating the complex number as a vector in Euclidean space destroys the covariant relationship between its real and imaginary parts. Hence, the study in [121]proposes a convolution operator that is equivariant to complex-valued scaling. It also highlights the difference between real-valued and complex-valued residual layers. In the field of complex numbers, shortcut connection is combined by channel-wise concatenation in a non-Euclidean manifold instead of addition in a vector space.
D. Others
Recently, the extension of real-valued network architecture into their complex-valued counterpart has been conducted. For instance, complex-valued DBN [122], [123], complex-valued stacked denoising autoencoders [127], complex-valued CapsNet [128], and complex-valued GAN [124]–[126]. For the complex-valued CapsNet, it is noteworthy that a complexvalued dynamic routing subnetwork is proposed and successfully decreases half of the trainable parameter number compared to real-valued routing models.
VI. APPLICATIONS OF CVNNS
In this section, we introduce and discuss the applications of CVNNs within the recent ten years in image classification and reconstruction, signal classification, identification and estimation, speech enhancement, wind prediction, and control systems. A summary of these applications is shown in Table IV,highlighting their strength and weakness.
A. Image Classification
CVNNs have been applied in dealing with the benchmark real-valued classification problem by using MNIST and CIFAR-10 datasets [80]. The classification accuracy of CVNNs is inferior to its real-valued counterpart. Also, a complex-valued CNN is also proposed and evaluated in the similar datasets [130]. The complex-valued CNN exhibits superior performance than its real-valued counterpart and its classification error decreases with the increase of kernel size.From the findings of these studies, the classification performance varies with the network structure. Besides, it is noteworthy to mention that [81] studies the performance of hybrid model, where real-valued convolutional filters are combined with complex-valued batch normalization. The hybrid model exhibits an improvement in the accuracy of realvalued CNN.
Besides, some studies extract the pixel information in an image before training the CVNNs. Kiziltaset al. [142] extract the HSV color space in the RGB scale, which makes it closer to human visual perception. This study compares HSV with other color space transformation approaches and concludes that single-layered CVNN with HSV is superior in skin detection. In addition, Akramifardet al. [7] also perform feature extraction before classifying the type of white blood cell from the microscopic images. Since different types of white blood cells possess various resolutions and colors,feature extraction before the neural network training can improve classification accuracy. They also compare the classification precision of the proposed method with RVNNs,where CVNNs exhibit superior performance over RVNNs.
In dealing with the face recognition problem, a CBP is designed by [147] to classify the input face images into their respective classes. Their study shows that the proposed algorithm achieves better classification performance and requires less hidden neurons than RVNNs, which reduces the computational time. Similarly, Amiliaet al. [148] propose the application of CVNNs in automatic gender recognition but conclude that there is no significant difference in classification accuracy between RVNNs and CVNNs in gender recognition.However, the training time for CVNNs is four times shorter than RVNNs, which demonstrates that the complex domain can perform faster computation in gender recognition than its real-valued counterpart.
Furthermore, CVNNs have been applied to classify the skeletal wire-frame of hand gesture [8], [149]. In the study of[8], they train the CVNNs with split-tanh activation function and LM algorithm. This study compares the classification ability between RVNNs and the proposed method with LVQ.Also, it compares the suitability of real-valued and complexvalued representations for hand gestures. LVQ is used to calculate the distance between input vectors of hand gestures,either in real-valued or complex-valued representation, where inputs with a higher similarity are grouped. They conclude that complex-valued classes are better separated than realvalued ones. On the other hand, CVNNs are used to detect and classify the open-close eye states, where color information in eye images is extracted and fed into CVNNs [150].
SAR is used to capture and detect the physical properties of the Earth’s surface, such as vegetation, volcano, and other environmental features. The captured image is then applied for natural disaster monitoring, topographic mapping, urban,and rural planning [46]. With the aid of complex-valued CNN,features in PolSAR and InSAR images can be classified automatically and accurately. In [96], a complex-valued CNN is proposed to exploit the complex-valued information for ATR and its performance is compared with its real-valued counterpart. Their proposed method improves the classification accuracy from 87.30% to 99.21%.
Moreover, Zhanget al. [29] not only propose PolSAR image classification by using a complex-valued CNN but also investigate the effect of adding one or more pooling layers in the network structure. The addition of the pooling layer reduces the classification accuracy from 96.2% to 90% as the pooling operation decreases the size of the feature map and subsequently cause information loss. They also study the influence of postprocessing techniques in the final classification map and improve the overall classification accuracy to 97.7%. Furthermore, Sunagaet al. [15] also conduct a study on the dependency on the size and number of the convolutional kernel in InSAR image classification and state that a small kernel might overlook some essential features.Other than that, Shanget al. [151] apply a variant of complexvalued CNN in PolSAR image classification, namely, SPF. It is composed of encoder and decoder path (i.e., downsampling and upsampling path) with postprocessing technique. SPF is applied on the final classification map, where it refines or converts the pixel of the map according to the predefined refinement condition. This pipeline successfully enhances the overall classification accuracy compared to its real-valued counterpart and the pipeline without SPF. Thus, it indicates that adding a postprocessing technique on the final classification map can enhance the classification accuracy.
In short, complex-valued CNN exhibits comparable or even better performance than its real-valued counterpart in image classification. Most of the studies apply the complex-valued CNN to classify images that are complex in nature, for instances, the PolSAR images. Complex-valued CNN exploits the amplitude and phase information in the images and improves the classification accuracy. The phase component in complex-valued image data carries essential information of the edges and shapes, while the magnitude component stores information of contrast and its frequency. Hence, one can identify the suitability of complex-valued CNN in performing image classification task by identifying the nature of data and the components (amplitude or phase) that store theinformation required for image classification [8], [152].
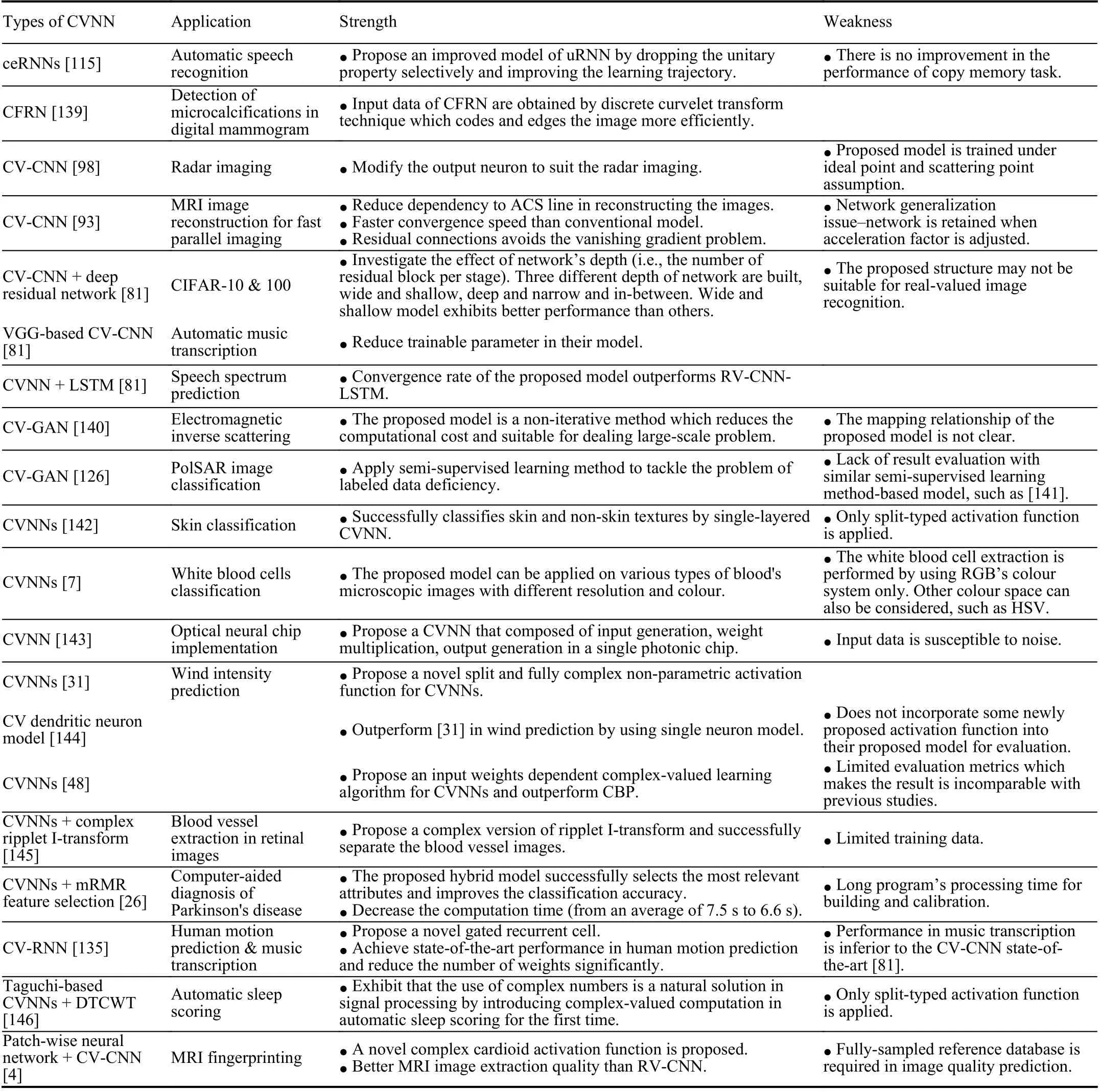
TABLE IV A SUMMARY OF SEVERAL LATEST APPLICATIONS OF CVNNS: COMPLEx-VALUED IS DENOTED AS CV WHILE REAL-VALUED IS DENOTED AS RV IN THE TABLE
B. Image Protection
Image protection has become a severe issue in this decade to establish a secure communication system. It is an image encryption and decryption system, where the information of the image is protected during the transfer. Yuanet al. [153]incorporate the idea of memristor-based neural networks into CVNNs and propose a novel neural network, namely,MCVNNs. The proposed method solves the exponential synchronization issue and achieves better performance in comparison with other state-of-the-art approaches.
C. Image Segmentation
Automatic image detection and segmentation have always been a hot research topic in the machine learning community.An extension into complex domain has also been explored and obtained comparable and superior performance than its real domain counterparts. Many approaches have been proposed to enhance the performance of automated image segmentation by image pre-processing technique, feature extraction and implementation of CNN and its variants. In the works of [154] and[155], they apply CVNNs with DTCWT as feature extractors in lung segmentation and blood vessel extraction. In addition,Ceylan and Ya?ar [155] improve their previously proposed method by using complex ripplet-I-transform [145] instead of DTCWT to extract the lines and ridges in the retinal image.This proposed method outperforms all the other state-of-theart methodologies.
A mammogram is commonly used in breast cancer detection, diagnosis and visualization. A framework that classifies the mammogram images is proposed [139], [156]. In their framework, they apply the FCRN based ensemble technique,where the FCRN is a complex-valued single hidden layer neural network with hyperbolic and exponential activation function at the hidden and output layers, respectively [72].They state that incorporating the ensemble technique into the final classification stage in the proposed method can improve classification performance and consistency. With the ensemble technique, the prediction of diverse FCRN is combined using hierarchical fusion, which makes the prediction result more generalized than an individual classifier. Similarly,Shiraziet al. [157] also propose a hybrid model of selforganizing map (SOM) and CVNNs for breast cancer classification. The input dataset is categorized into a few clusters by using SOM based on their similar features, and the training of CVNNs is performed based on the clusters.
D. MRI Image Reconstruction
CNN has shown rapid and robust performance in MRI image reconstruction and various CNN architectures are proposed in the real domain to reconstruct MRI images from the accelerated scans. Although the MRI data is complexvalued, most of the proposed deep learning frameworks do not support complex-valued and cause information loss. Thus,complex-valued CNN should be applied to avoid the discard of complex algebraic structure in the data. The work in [28],[89] and [93] extends deep residual network, U-Net [158] and unrolled networks [159] into complex domain. In the work of[28], [89], they adopt the U-Net framework with complexvalued MRI signal and achieve a higher average SSIM than its real-valued counterpart and the conventional MRI image reconstruction approach. Furthermore, the proposed deep residual network, which is also known as DeepcomplexMRI[93], achieves an even higher SSIM of 0.920 than the U-Net framework proposed by [28] with SSIM of 0.907. In addition,one of the drawbacks of the classical approach that the sensitivity and dependency of ACS lines in the image reconstruction is resolved in the proposed method. Deepcomplex-MRI can reconstruct MRI images with less noise signals at a higher acceleration than the state-of-the-art parallel imaging method.
E. Signal Classification and Identification
Generally, most of the collected signals, such as electromagnetic, lightwave, radio frequency, and sonar echo signals are in complex domain [160]. Due to the nature of these input signals, it is more suitable to apply CVNNs than RVNNs to preserve the information carried by the phase and magnitude components.
In the sonar echo signal classification and solar irradiation forecasting, the study in [161] applies CWNN, which is a wavelet network composed of one hidden layer and wavelet function as its activation function. Such a network is widely used in processing signal data or acting as a feature extractor.Additionally, the work in [162] suggests the need of extracting and transferring the complex-valued features to sparse Fourier transform before being classified by CWNN in the sonar echo signal classification. The proposed model exhibits superior classification performance than the model that uses discrete Fourier transform as their feature extractor. Fully CWNN, on the other hand, is proposed and applied in solar irradiation forecasting [163]. The proposed approach is evaluated with RVNNs, CVNNs and CWNN. Fully CWNN achieves better forecasting ability by fully utilizing the correlation between imaginary and real components in the hidden layer during training.
Besides, the emerged proliferation of wireless networks in society has brought up some issues in cyber-security. In order to identify the radio frequency sent by a wireless device, a radio frequency fingerprinting algorithm is proposed [164].They design and study four complex-valued models. Their findings show that a model with spectral augmentation of the input signal can improve the validation performance.
1) EEG Signal Processing:Moreover, the combination of wavelet transformation and CVNNs is also applied in processing EEG signal for epilepsy diagnosis. In the study of[165], DTCWT extracts features and passes them to a statistical feature selector, finally, into the CVNNs. DTCWT solves the drawbacks of wavelet transformation: shift sensitivity, poor directionality, and the absence of phase information. Such hybrid model successfully achieves excellent classification performance and reduces the computational time compared to RVNNs with wavelet transformation. With the achievement of [165], Aizenberg and Khaliq [166] alter the previous combination by replacing the DTCWT and CVNNs with Fourier transform and MLMVN,respectively. The result shows that the Fourier transform can perform as well as DTCWT and achieves a stable 100%classification accuracy for both experiments using Fourier transform and DTCWT. Such performance is achieved due to the excellent property of MLMVN, which is the derivativefree learning and higher functionality than conventional MLP in stabilizing the classification performance of the model[167].
Also, EEG signals are used to provide automated sleep scoring and classify the sleep stage [146]. Similarly to the previous approach, DTCWT is used to extract features in the EEG signals and the statistical features are classified by CVNNs.
2) Glucose Concentration Prediction:A non-invasive,adaptive glucose concentration estimator based on millimeter wave is proposed [168]. In the proposed model, they expose the test sample (glucose water) to the millimeter wave and the transmitted wave is collected by the antenna. The magnitude and phase of the transmitted wave vary with different glucose concentrations. Then, they pass the transmission data into a single-layered CVNN to estimate the glucose concentration.This study successfully builds an estimator with good generalization ability and further clinical improvements should concentrate on its application to the medical field.
3) Communication Signal:In the communication signal field, complex-valued CNN is applied for detecting the transmitted signal in the MIMO next generation wireless network [97]. With the aid of the max-pooling layer in complex-valued CNN, the proposed framework reduces the computational complexity by 14.71% compared to the conventional method, ML detector. Changet al. [100] propose the use of complex-valued CNN in signal equalization, which recovers the communication signal from noised signal influenced by wireless channel.
F. Speech
CVNNs are suitable for processing the speech signal as they fully represent the magnitude and phase information. Tsuzukiet al. [5] propose a sound source localization approach by using CVNNs. Two microphones collect the sound signal and the origin is localized through FFT and CVNNs. Moreover,complex-valued U-Netalso exhibits superior performance to the conventional approaches in speech enhancement, where clean speech is separated from the given noisy speech [101].Besides, Hayakawaet al. [169] build an acoustic modeling for speech recognition, which comprises of both complex-valued and real-valued layers. They also propose a batch amplitude mean normalization to accelerate and stabilize the network training. The proposed method outperforms its real-valued counterpart, even under noise conditions.
Meanwhile, a contrary result is reported in [170], where CVNNs hardly show any performance gain compared to RVNNs in performing the speech enhancement. In the study of Drudeet al. [170], they assess the appropriateness of using CVNNs in speech enhancement. CVNNs applied in this study are solely the direct extension of RVNNs, in which no model optimization is performed to improve the performance of CVNNs. From their findings, they conclude that direct extension of RVNNs into complex-domain does not enhance the performance of speech enhancement, yet, it imposes more real-valued multiplication than RVNNs [170].
In addition, several automated Parkinson’s disease identification methods are proposed with voice or speech datasets as the input of CVNNs. A Mc-FCRBF is proposed and the addition of meta-cognitive part successfully reduces the error in disease identification [171]. It is then followed by [26] who proposes a feature selection algorithm, namely, mRMR, to eliminate the less relevant features before the implementation of CVNNs. The performance of mRMR is compared with other feature selection algorithms and it exhibits a superior classification performance of 98.12% to others. Moreover, a feature weighting algorithm combined with CVNNs [172] is proposed to cluster similar data together, which achieves a better classification result of 99.52% than the previous study[26]. The feature weighting method applies the KMC algorithm to calculate the cluster center and uses the distance between data points and its cluster center for the weighting process.
G. Wind Prediction
Recently, artificial intelligence algorithms and neural networks have been widely applied in the prediction of wind speed, power, and direction. For instance, the work in [173]demonstrates the effectiveness of CVNNs in predicting wind speed and direction.
Sepasiet al. [6] also propose two wind power forecasting models, namely, parallel-series CVNN-based model and parallel-series spline-based model. These models use CVNNs for parallel forecasting, while the model with spline technique is also applied in series forecasting. They obtain the output of the proposed model by combining parallel and series forecasting techniques. The primary prediction key of these two models is searching the day of week, which has the most similar weekly index with the forecast day. Their result demonstrates that parallel-series CVNN-based method outperforms the others.
On the other hand, ?eviket al. [174] propose a wind power forecasting system that makes a day ahead hourly prediction at seven wind power plants (WPP). The proposed model is evaluated with RVNNs. It outperforms RVNNs in forecasting the wind power at all WPP.
Moreover, a Mc-FCRBF, which is a combination of selfregulatory learning mechanism and a fully CRBF network, is proposed to predict the wind profile [175]. The prediction error is successfully reduced with the addition of a selfregulatory learning mechanism in the network.
Researchers also propose and apply different activation functions to assess the performance of wind prediction. In[34], five different types of ReLU activation functions (OR,AND, sum, product, and split type) are used in wind prediction of 6 and 12 hours ahead. Since the size of the activation area varies with the types of activation function,more trainable parameters are required to be updated with the increase of activation area. In their findings, OR and ANDtyped outperform others in 6 and 12 hours ahead prediction,respectively. In addition, a non-parametric activation function,KAF, is proposed and evaluated with wind intensity prediction task [31]. The proposed split-KAF significantly outperforms all the other conventional activation functions(split-ReLU, modReLU and split-tanh).
H. Control System
Neural network in hardware implementation has gained attention in various fields, for instance, adaptive control design [176]–[178] and MIMO control system [179]. Time delay and synchronization of systems are important considerations in designing effective controllers and implementing them on some practical applications. However, time delay is inevitable due to the finite switching speed of the amplifier,which may cause oscillation, chaos or even instability in the systems [180], [181]. Synchronization, on the other hand,refers to the identical state trajectory of two systems, in which one of the systems is designed to simulate the dynamic behavior of another system. To design controllers that achieve synchronization, various type of studies are conducted to investigate the dynamical behavior of CVNNs and improve the techniques in controlling and synchronizing the CVNNs.The improvements include adaptive control, pinning control,intermittent control, event-triggered control, and impulsive control [182]–[187].
I. Other Applications
CVNNs are also applied in performing prediction tasks in protein secondary structure, finance time series, soil moisture level, and audio prediction to enhance MP3 encoding. CVNNs exhibit better prediction performance than their real-valued counterparts. Various CVNNs are adopted for these applications, for instance, MLMVN is applied for soil moisture prediction [188], FCRN is used in protein secondary structure prediction [189], while CVFNT is applied in building a financial time series prediction model [190]. In the financial time series prediction model, CVFNT is evolved by a modified genetic algorithm and artificial bee colony algorithm.Besides, insertion of CVNNs module into MP3 encoder preserves the audio quality and, simultaneously, reduces the file size (i.e., increases the compression ratio) [191].
Moreover, the work in [192] applies CVNNs in the identification of organic chemical compound structure. The hidden layer of the proposed network is composed of a set of boolean logic complex neurons, in which each neuron consists of a boolean function to determine which category of substances it belongs to. Besides, CVNNs are also applied in medical images forgery detection [193] and provides a rapid solution for complex-valued linear equation system [194]. Zhanget al.[143] successfully implement CVNNs onto an optical neural chip that allows the execution of complex-valued arithmetic by optical interference in the optical computing platform.Their study demonstrates the potential of complex-valued optical neural networks to feature a versatile representation in handwriting recognition and some classification tasks. It possibly leads to near-term quantum computations, where optical interferometers networks realize the perceptrons in their model.
VII. CVNNS CHALLENGES AND FUTURE DIRECTIONS
Understanding the existing challenges of CVNNs is a key to further unleashing its potential ability and creating future research topics. In this section, we discuss some challenges faced by CVNNs and their likely future research avenues.
The challenges and suggested future directions of CVNNs are as follows:
1) Design of Activation Function
An obvious challenge of CVNNs is the design of activation function. Due to Liouville’s theorem, we are required to compromise one of the crucial properties of activation functions (either the boundedness or analytic). In addition,fully complex activation functions are more favorable than the split-typed to represent both magnitude and phase components completely. Throughout the years, attempts have been performed by designing various activation functions for CVNNs, for instance, the cardioid function [4] and non-parametric function, KAF [31]. This particular area is still an open research field since activation function is regarded as an essential element in providing neural networks nonlinearity. The activation function that has shown extraordinary performance in real cases could be extended into the complex domain, for instance, the adaptive piecewise linear unit [195], [196].
2) Complex-Valued Learning Rate
CVNNs have all the input data and parameters in complex numbers, which leads to a question: Is that necessary to also express the learning rate in complex numbers? To adequately address this question, Zhang and Mandic [197] study the merit of using complex-valued learning rate by evaluating the CVNNs with real-valued and complex-valued learning rates.They highlight that the complex-valued learning rate extends the search area of the complex gradient descent algorithm from half-line to half-plane. Such extension also provides an extra degree of freedom for the algorithm to escape the saddle points. Recently, some studies on complex-valued learning rate have been actively published [74], [75]. These findings suggest a new research direction for developing a more generalized, adaptive complex-valued learning rate algorithm,which can be applied in CVNNs and their variants.
3) Non-Gradient-Based Learning Algorithm for CVNNs
Apart from the complex-valued learning rate, the learning algorithm of CVNNs could be a potential research topic. The conventional backpropagation algorithm requires gradient computations, which is an obstacle in CVNNs since some activation functions are not analytic everywhere on the complex plane. Therefore, we recommend to explore some non-gradient-based algorithms, for instance, the evolutionary algorithms in the network training [198]–[205].
4) Potential of Biological-Based Model of CVNNs
In Section II, we discuss the motivation of CVNNs from a biological perspective. The action potential used to transmit neuronal information in human is similar to the representation of complex numbers, which are composed of both magnitude and phase components. When the action potential is in an excitatory condition, signals at the same phase add constructively and prevail over out-of-phase signals. Such a concept provides an idea to CVNN configuration when the out-ofphase input signals could generate an inhibitory message to the neuron and, thus, be ignored [19]. Recently, Gaoet al.[144] propose a fully complex dendritic neuron model, which mimics a human neuronal information transmission mechanism. Their model outperforms conventional CVNN on complex-XOR classification, nonminimum phase equalization, and wind prediction problem. Such achievement may be credited to the biological representation in their network structure.
Additionally, spiking neural network (SNN) is also a biologically plausible neuronal model that uses the timing of signals (or spikes) in the biological neural system to process information [206]. Spike-timing dependent plasticity (STDP)is a common learning rule of SNN, and it has been applied in a complex-valued neuron recently [207]. Their proposal enables the spontaneous formation and dissolution of phase assemblies, an important property of a biologically plausible extension of the Hopfield network. This finding suggests the possibility and efficacy of using complex numbers in SNN.
Thus, we strongly encourage exploring such biologically plausible models to tackle more complex real-world problems[208]–[220].5) Numerical Issue of CVNNs
Another challenge of CVNNs is the numerical issue during the training process. Such issue has been reported in the training of conventional CVNNs [79] and complex-valued CNN [33]. The training model in both studies has a high sensitivity to the random weight distribution, which causes the training performance to be poor and inconsistent. The complex-valued batch normalization and weight initialization have been proposed to mitigate the dependency of parameters in neural networks [80], [81]. However, the performance of their proposal is not consistent, where it improves the classification accuracy in complex-valued CNN, but not in complex-valued MLP. Hence, future studies should focus on solving this issue to improve the training consistency of CVNNs. Additionally, neural architecture search is also an effective way to find the optimal set of parameters in neural networks [221].
VIII. CONCLUSION
This paper comprehensively reviewed the learning mechanisms, activation functions of CVNNs, and their applications in wind prediction, speech enhancement, image segmentation,MRI image reconstruction, image and signal classification,control systems, and others. Additionally, we provided a review on the variants of CVNNs, such as complex-valued CNN, RNN, residual neural networks, and CapsNet. We also highlighted the importance of the phase component in complex-valued signals and related it with the human neuronal transmission mechanism. Furthermore, some possible outlooks of CVNNs were given in terms of the incorporating non-gradient-based learning algorithm, designing activation functions, and the exploring the potential of biological-based CVNNs.
This paper targets a broad spectrum of audiences from RVNNs and the CVNNs communities. Researchers currently working in the CVNNs field will benefit from all the summarized works as a foundation to improve their current studies. On the other hand, researchers in the RVNNs field will have better understanding on the current development of CVNNs and appreciate the importance of the complex-valued signals. We hope that it would be a great starting point for them to extend their studies into complex domain.
 IEEE/CAA Journal of Automatica Sinica2022年8期
IEEE/CAA Journal of Automatica Sinica2022年8期
- IEEE/CAA Journal of Automatica Sinica的其它文章
- Visuals to Text: A Comprehensive Review on Automatic Image Captioning
- Cyberbullying and Cyberviolence Detection: A Triangular User-Activity-Content View
- Networked Knowledge and Complex Networks: An Engineering View
- Battery Full Life Cycle Management and Health Prognosis Based on Cloud Service and Broad Learning
- Estimation Based Adaptive Constraint Control for a Class of Coupled String Systems
- Multi-Attention Fusion and Fine-Grained Alignment for Bidirectional Image-Sentence Retrieval in Remote Sensing
