Liping Tang

Abstract.Language use and pragmatic inference frequently involve similarity reasoning.Based on the classical Lewis’s signaling game,we propose a novel signaling game based on the similarity reasoning and the propositional contents of the signals.Within the new similaritybased signaling game,we discuss that the new game can select the best signals even when the available signals are less structured than what we want to communicate.Moreover,we apply our model to Horn’s analysis of division of labors in Pragmatics.

1 Introduction

Language learning and language use frequently involve analogical reasoning.Analogical reasoning is fundamental to human thoughts.It relies on the comparison of two objects,or two systems,then highlights the similarity between them and makes prediction.([2]) We call it similarity reasoning in this paper.According to Gardenfors’s concept space ([6]),concept formation relies on a similarity comparison between the features of objects.Meanwhile,similarity reasoning is also widely applied in the word-sense disambiguation in machine learning ([1,12]) and game theoretical pragmatics([14,11]).Hence,our new signaling game emphasizes this similarity reasoning in the language use.

As we consider natural language,what can be said is often less than what we want to communicate.According to the principle of least effort([21]),the language is always not fruitful enough to accurately express everything we want to express.Most of the time,we have to choose the closest word from the available ones to express our ideas.The process involves the comparison between the available words and the trade-off between the available words and the information we want to transmit.

Signaling game pioneered by David Lewis([13])has been applied in the study of various language features and language learning in philosophy,game theory and logic.The study of language includes the study of ambiguity([16]),vagueness([15,14]),compositionality ([5]).The exploration about language learning addresses learning in social network([22,20]),learning communication contexts([19,3])and learning concept structures([11]).

The traditional Lewis signaling game captures a rather simple communication scenario.In this model,there is a finite set of states.For each state,there is an appropriate action for that state.There is a sender,who is aware of the state and can send one signal to a receiver.The receiver is unaware of the state and must choose an action.The receiver can condition her choice of actions on the signal sent by the sender.Both the sender and the receiver have common interest,they would like the receiver to take the appropriate action given the state.

Within this model,the states,the signals and the acts are all assumed to be abstract objects.There is no content and structure within them.Because of this feature,there are several disadvantages of applying this model in the study of natural language.Firstly,we cannot talk about the meanings of the signals within the model.The meanings of the signals are only implicitly expressed by the equilibrium strategies of the game.Moreover,without the pre-assumed meanings of the signals,there are many equilibria in this game,some of which are inferior than others with respect to the outcomes.Secondly,we cannot talk about the connections between the states and the signals or between the signals and the acts within the model,since they are all abstract symbols.Lastly,the Lewis’s signaling game does not allow us to discuss about the differences of the signals within the model.This is so because the format of signals in the model has no effect on the utilities.

To overcome these disadvantages,we propose a new signaling game based upon propositional logic.The states,signals and acts are all represented by propositional formulas.In addition,the format of the signals affects the players’utilities.There are two main advantages of doing this.

Firstly,the new model can discuss more complex messages by using propositional formulas.The expressiveness of the model is significantly improved.A similar idea has already been mentioned in [17,18].Meanwhile,the number of separating equilibria can also be reduced by considering the different meanings of the messages.

Secondly,using propositional logic and the entailment measurement between formulas from Dalal ([4]) and Hunter ([10]),we can discuss the similarity connections between the states and the signals and between the signals and the acts.As a result,the sender can choose a proper signal upon a specific state.That is,the sender chooses the signal by comparing the similarity between a given state and the signals,such that he can choose the most accurate expression.On the other hand,upon receiving the signal,the receiver chooses the most accurate explanation by comparing the similarity between the signals and the possible explanations.A successful communication requires the coordination between the states and the explanations through certain signals.

Moreover,the way we define the utility function in the new game is inspired by Horn’s division of pragmatic labors.([9])In a successful communication,a message needs to be sufficient(Q-principle:say as much as you can)as well as necessary(Rprinciple:say no more then you need).Such an idea is reflected in the new utility functions of the new game.We also discuss the possible connections between our game and Horn’s theory.

The rest of the paper is organized in the following way.Section 2 is a review of Lewis signaling game.In Section 3,we introduce the propositional logic and the model entailment measurement that we shall use in the later sections.Section 4 introduces our new signaling game based on the propositional logic and the similarity reasoning.In Section 5,we connect our model with Horn’s division of pragmatic labors.The paper ends with a short conclusion.

2 Review of Signaling Game

The traditional Lewis’s signaling game([13])provides a baseline model to capture a rather simple communication scenario.In this model,there is a finite set of states.For each state,there is an appropriate action for that state.There is a sender,who is aware of the state and can send one of a finite set of signals to a receiver.The receiver is unaware of the state and must choose an action.The receiver can condition her choice of actions on the signal sent by the sender.Both the sender and the receiver have common interest,they would like the receiver to take the appropriate action given the state.

Formally,a signaling game can be defined as follows.

Definition 1.A signaling gameGis a tuple{T,M,A,{S,R},σ,U},in which,

·Tis a finite set of states;

·Mis a finite set of signals;

·Ais a finite set of actions;

· There are two players:a sender(S)and a receiver(R);

· The sender’s action ism ∈Mand the receiver’s action isa ∈A1Whenever there is no confusion,we use the message and action symbols m and a as the players’strategy function as well,that is m:T→M and a:M→A.;

·σis a common prior onT;

· We assume that the players share the same utility,that is

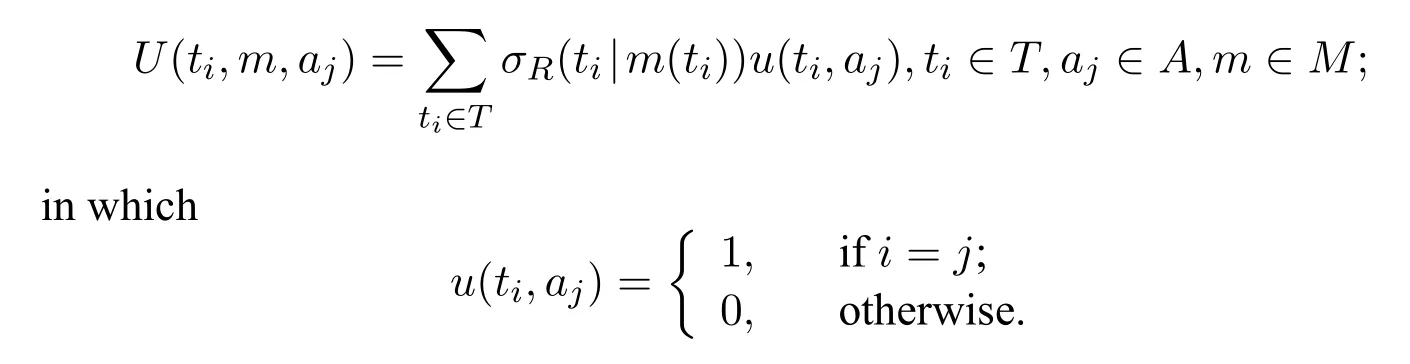
σR(ti|m(ti))represents the receiver’s conditional beliefs about the states after observing the sender’s messagem(ti).u(ti,ai)measures the information matching between the states and the acts.If the state and the act matches,then the payoff is 1.Otherwise,it is 0.The players’utility is the expected payoffs based on the receiver’s beliefs about the states.

From the game theoretical point of view([7]),signaling game is a typical example of Bayesian dynamic game with incomplete information.Following the standard analysis of the equilibrium,we specify the players’ beliefs and their best response strategies as follows.

Definition 2.(1) After observing the messagemj ∈Mfrom the sender,the receiver has a belief about the type of the sender.This belief can be expressed by the probabilityσ(ti|mj),such thatσ(ti|mj)≥0 for anyti ∈ Tand

(2) Given such a belief,the receiver’s best strategya*(mj)is to solve the following question,

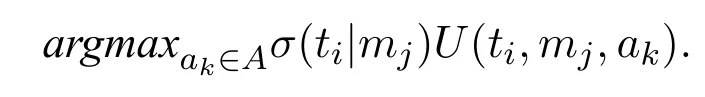
(3) For each stateti ∈T,the sender’s optimal strategym*(ti)solves

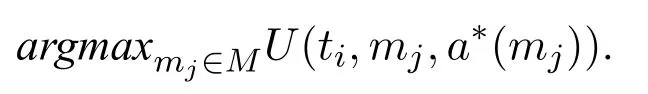
(4)σ(ti|mj)follows from the Bayes’s rule.

Definition 3.A pure-strategy Bayesian equilibrium in the signaling gameGis a pair of strategies(m*,a*)and a beliefσ(ti|mj)satisfying(1)through(4)in Definition 2.

There are two kinds of equilibria in signaling games,namely,pooling equilibrium and separating equilibrium.We use the following example to illustrate these two notions.

Example 1.The simplest Lewis’s signaling game consists of two states:{t1,t2},two signals{m1,m2}and two acts{a1,a2}.

An instance of“separating equilibrium”in this game has the following pattern

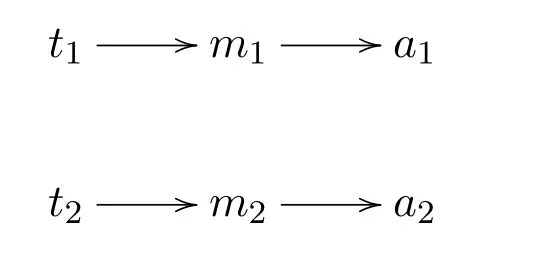
When statet1occurs,the sender sendsm1.By receivingm1,the receiver takesa1.Similarly,when statet2occurs,the sender sendsm2.Under this equilibrium,all the information about the states is communicated successfully between the sender and the receiver.Meanwhile,the players receive the highest payoff.

In addition,the game has a“pooling equilibrium”.The following is the pooling equilibrium of this example.

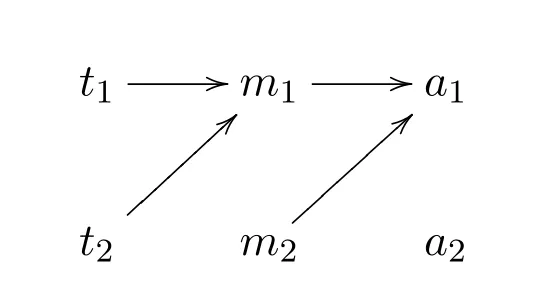
In this equilibrium,the sender always sends the same signal and the receiver takes the same action by ignoring the signal.As a result,the information is not fully communicated,pooling equilibrium of this kind features ambiguity,m1means both statet1and statet2.Furthermore,these equilibria are Nash equilibria and are therefore stable in a certain sense.Neither the sender nor the receiver can unilaterally improve their situation by switching their strategies.

Though Lewis’s signaling game provides a general characterization of communication and a theory of language meaning,the language in this model has no internal structures.In classical signaling games,the states,the signals and the actions are abstract objects.There is no structures within the states and the actions.The signals have no pre-assumed meanings.One consequence of these assumptions is that there are many equilibria in this game.For instance,if we switchm1andm2in the above mentioned separating equilibrium,it is still a separating equilibrium.

In this paper,we construct a signaling game based upon propositional logic such that we can talk about the propositional contents about the states,acts and the signals.Moreover,we can define the relationship between the states,the signals and the actions by using the properties in propositional logic.To achieve this goal,we need some basic notions in propositional logic.In the next section,we give a brief introduction of the propositional logic as well as the similarity reasoning that we will use in our model.

3 Similarity Reasoning in Propositional Logic

The similarity reasoning applied in this paper follows from Hunter’s discussion about the entailment relationship between formulas.([10]) A similar idea can trace back to Dalal’s work on belief revision.([4])Since the entailment relationship measures how common two formulas(or sets of formulas)are with respect to their models,we call it similarity measurement in our paper.

Throughout the paper,we usep,q,h....to represent atomic propositions,α,β,γ,...to indicate the propositional formulas andX,Y,...,to denote the set of formulas.Deduction in classical propositional logic is denoted by the symbol?.

Definition 4.A language of the propositional logicLconsists of the following.

(1) A finite set of atomic propositions;

(2) A set of connectives{∧,∨,?,→}.

Since we want to express various expressions in natural language,therefore,we use all of the connectives in the model.The well formed formulas based onLis defined in a standard way as in propositional logic.

Definition 5.Given a finite set of atomic propositionsA,a modelwof a formulaφ(or a set of formulasX)is a subset ofA,such that?p ∈w,pis assigned true and?p ∈Awis assigned false.LetI(X)=P(atom(X))2P(X)represents the power set of X.be all the models ofXdelineated by the atoms used inX,whereatom(X)represents all the atoms inX.

Now we can define the entailment measurement between sets of formulas based on the models of propositional formulas.

Definition 6.LetM(X,Y) be the models ofXinI(Y).Formally,M(X,Y)={w ∈I(Y)∧X},where|=is the logical entailment in propositional logic,∧Xrepresents the conjunction of all the formulas inX.Then,the degree of entailmentofXforY,denoted asE(X,Y)is defined as follows:

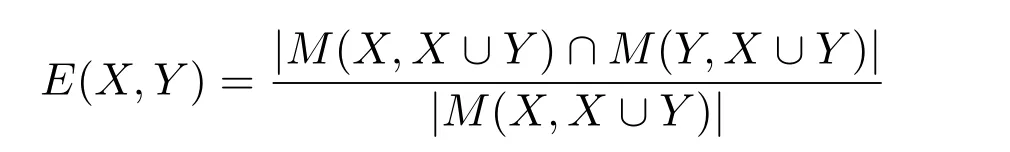
in which,given any set X,|X|represents the number of elements in this set.

Example 2.SupposeX={p},Y={p∨q}.Thus,I(X∪Y)={{p},{q},{p,q},?},M(X,X ∪Y)={{p},{p,q}}andM(Y,X ∪Y)={{p},{q},{p,q}}.Therefore,E(X,Y)=1,whileE(Y,X)=2/3.

We call the degree of entailment between two sets as similarity measurement.The similarity measurement has the following properties.

Proposition 1.Let X,Y and Z be the sets of classical propositional formulas,then the followings hold:

(1) 0 ≤E(X,Y)≤1;

(2)X ?∧Y iff E(X,Y)=1;

(3)X ??∧Y iff E(X,Y)=0.

Proposition 1 shows that there is a relationship between the similarity measurement and the logical entailment.Because of this feature,we can connect this measurement to Horn’s pragmatic principles in conversation in later sections.

It is also obvious that the similarity measurement is not symmetric.That is,given anyX,Y,E(X,Y)is usually not equal toE(Y,X).

Definition 7.We represent a propositional logic with a similarity measurement denoted bySLas a pairSL=(L,E)in which

(1)Lis a propositional logic defined onL;

(2)E(X,Y)is a similarity measurement ofXforY,in whichX,Yare formulas(or sets of formulas)inL.

4 A Similarity-Based Signaling Game

Two reasons motivates us to consider a similarity-based signaling game.Firstly,analogical reasoning appears very frequently in language learning and language use,which is fundamental to human thoughts.As Gardenfors stated in his theory of concept space([6]),concept formation also relies on a similarity comparison between the features of objects.

Secondly,regarding natural language,the language is always not fruitful enough to accurately express everything we want to express.In addition,there are numerous uncertainties in language,such as ambiguity,vagueness and synonymy.Hence,what we can say is often much less accurate than what we want to communicate.As a result,we have to choose the most appropriate word from the available ones to express our ideas.During this decision process,it is often observed the comparisons between the available words and the trade-offs between the available words and the information we want to transmit.

On the other hand,in Lewis’s signaling game,the signals have no effect on players’ utilities.As a result,the model can not distinguish different forms of signals.Therefore,we need to modify the Lewis’s signaling game such that we can compare between different signals with respect to the contents of the signals.In addition,the contents of the signals should affect the utilities.

Therefore,in this section,we define a similarity-based signaling game.Comparing to the signaling game defined in Section 2,there are two main changes we made in the new game.

Firstly,we define the states,the signals and the actions in the standard signaling game with propositional contents.Formally,we use propositional formulas representing the states,the signals and the actions in the signaling game.

Secondly,we redefine the utility function in the signaling game such that the similarity relations between the states and the signals,and between the signals and the actions can be reflected in the utility function.By using the similarity measurementEdefined in Definition 6,we emphasize the similarity comparison of propositional contents in communication.As a result,the choice of the signals affects players’utilities as well as the outcome of the game.

These two changes are included in the new definition of our game presented below.

Definition 8.A similarity-based signaling gameSGis a tuple

SG={SL,T,M,A,{S,R},σ,U},in which

·SLis a propositional logic with a similarity measurementE;

·Tis a finite set of states,t ∈Tis a propositional formula inSL;

·Mis a set of signals,m ∈Mis a propositional formula inSL;

·Ais a finite set of actions,a ∈Ais a propositional formula inSL;

· There are two players:a sender(S)and a receiver(R);

·σis a uniform prior distribution overT,σis the common knowledge between the players3Throughout the paper,we assume σ is a uniform distribution over T.It is easy to extend the model for other prior distributions.;

· The sender’s action set isMand the receiver’s action set isA;

· We assume that the players share the same utility,that is

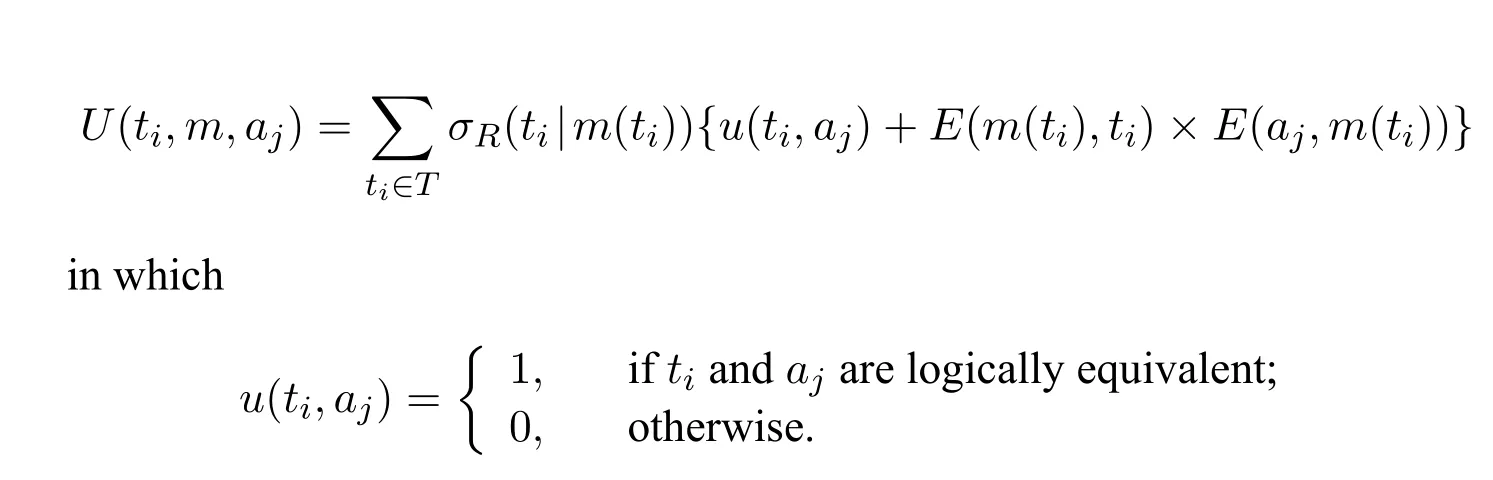
The utility function consists of two parts.The first partu(ti,aj)characterizes the information matching between the states and the acts.If the states and the acts are logically equivalent,then we say the information transaction is successful.

The second partE(m(ti),ti)×E(aj,m(ti)) in the utility function represents the similarity between the states and the signals and between the signals and the acts with respect to their propositional contents.We can calculate the similarity measure ofm(ti) forti,withE(m(ti),ti),and the similarity measure ofajform(ti)byE(aj,m(ti)).The reason we consider the multiplication of these two measures is becauseE(m,t)≤1 andE(a,m)≤1,thereforeE(m,t)×E(a,m)≤1,which yields the same maximum asu(t,a).Hence,the two parts in the utility function have the same impact on the overall utility.

The way how we define the similar measurement is inspired by Horn’s devision of pragmatic labors([9]).According to Horn,Grice’s maxims can be replaced with two fundamental principles:say as much as you can(the Q-principle)and say no more than you must(the R-principle).([9,8])The Q-principle states a sufficient condition about the quantity of the message,while the R-principle states a necessary condition about the relevance of messages.

On the other hand,our similarity measurement has a close connection with the logic entailment.According to Proposition 1,given a set of formulasXandY,E(X,Y)=1 if and only ifX ?∧Y.Thus,Xrepresents the sufficient condition ofY.Therefore,we define that the sender is to choose a message implying the state given the statetasE(m,t).Also,from the receiver’s point of view,the message provides a necessary condition for his interpretation of the message,namely,E(a,m).Regarding the connection between our game and Horn’s theory,we will discuss it more in Section 5.

In the new game,the states,the signals and the acts are all represented by propositional formulas.Hence,we can express the meaning of the signals as the propositional contents.The acts in the form of propositional formulas can be understood as the receiver’s interpretations of the signals.

The definition of Bayesian equilibrium forSGis defined in the same way as in Definition 3.

Definition 9.A pure-strategy Bayesian equilibrium in the signaling gameSGis a pair of strategies(m*,a*)and a beliefσR(ti|mj)satisfying(1)through(4)in Definition 2.

We use the following examples to illustrate the notions in theSGgame.

Example 3.Given aSGgame,suppose the set of the states is{t1：p∧q,t2：p ∨q},the set of signals is{m1：p∧q,m2：p∨q},and the set of the acts is{a1：p∧q,a2：p∨q}

Obviously,the equilibrium strategy ism(t1)=m1,m(t2)=m2,a(m1)=a1anda(m2)=a2.That is

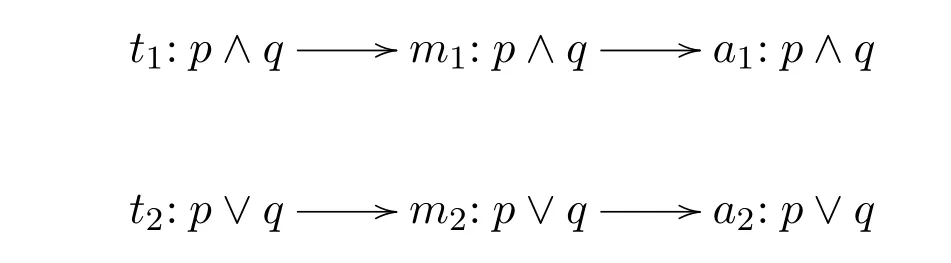
This is a separating equilibrium under which the information is completely transferred from the sender to the receiver.Given the priorσas a uniform distribution overT,the utility under this equilibrium is

It is worth commenting more on this simple example and emphasizing the differences between the newSGgame and the classical Lewis’s signaling game.

(1) Since the propositional contents of signals are specified inSG,the number of separating equilibria is reduced to only one in Example 3.While in Example 1 with the similar setting,there are two different separating equilibria under which the signals switch meanings in the two equilibria.

(2) Example 3 is a special case that the signals take exactly the same form as the states.Normally,the signals may have different forms as the states.Example 4 illustrates this point.

(3) It is even possible that the set of the states does not need to be exactly the same as the set of the acts.As a result,the elementu(t,a) may take values rather than just 0 or 1.We can measure the similarity oftandaby calculatingE(t,a)andE(a,t).We leave this point as future work.

As we mentioned before,natural language is often not exactly the same as the information we want to communicate.Therefore,the situation in Example 3 hardly occurs in natural language.Hence,we have to consider the situation where the set of signals are different from the set of the states,which is characterized in Example 4.

Example 4.Given aSGgame,suppose the set of states is{t1：p,t2：p ∨q},the set of signals is{m1：p,m2：q},and the set of acts is{a1：p,a2：p ∨q}.

We calculate theEmeasure for each state,signal and act pairs as follows.

E(m1,t1)=1,E(m2,t1)=E(m1,t2)=1,E(m2,t2)=1;E(a1,m1)=1,E(a2,m1)=E(a1,m2)=E(a2,m2)=

Figure 1 :Extensive play for each state(Example 4)

In Figure 1,we represent the play of the game as an extensive game for each state.The sender knows the true state while the receiver does not know.Andσ(t1)=σ(t2)=0.5.The number associated with each act is the payoff for the players.

The equilibrium of this game can be found in this way.For the receiver,oncem1is received,he decides the action by calculating the expected utility of choosing each act.Since he does not know which state is actually occurs,he calculates the expected utility of choosinga1with respect to the posterior probability on the states,which we assume them to be equally likely.Therefore,EU(a1)The expected utility of choosinga2isEU(a2)=Hence,he should choosea1form1.In the similar way,we can calculate that the receiver choosesa2form2.By assuming the receiver’s strategy,the sender’s best strategy is to sendm1fort1andm2fort2.

Therefore,there is a separating equilibrium for this game that ism(t1)=m1,m(t2)=m2,a(m1)=a1,a(m2)=a2.

Example 4 shows that our model can induce a successful communication even if the set of the signals is not exactly the same as the set of the states.At the same time,the equilibrium sustains our intuition about the propositional contents of the signals.

From Example 4,it is obvious that when the communication is successful,the similarity measurementE(m,t)×E(a,m)also achieves the optimal.This result can be generalized.

Proposition 2.Given a SG game,if the separating equilibrium exists,then the message m used in the equilibrium is the most similar signal,that is,m maximize∑E(m,t)×E(a,m).

Proposition 2 shows that our new signaling game can select the best signals for a successful communication in terms of our similarity measurement.

5 Horn’s Division of Pragmatic Labors

In game-theoretical pragmatics,the sender must take into account how the receiver would interpret the signals when he chooses the signal.Meanwhile,the sender should consider the available set of signals and the fact that the sender chooses the signal strategically.

On the other hand,the similarity measurement defined in our game not only measures the common part of two propositions,but also implies the entailment relationship between two propositions.Recall the definition of the similarity measurement in Definition 6 and the features of the measurement in Proposition 1,the following holds.

Given a set of propositional formulasX,andY,E(X,Y)=1 if and only ifX ?∧Y.By using this property,we can discuss about the Horn’s division of pragmatic labors,then connect the equilibrium strategy in our new signaling game to the pragmatic principles in Horn’s theory.

As we mentioned before,according to Horn’s division of pragmatic labors,Grice’s maxims can be replaced with two fundamental principles:say as much as you can(the Q-principle)and say no more than you must(the R-principle).([9,8])These two principles can be characterized by our similarity reasoning as follows.

Definition 10.In a two-player signaling gameSG,the Q-principle corresponds to the sender’s strategy (the message implies the state information,i.e.,the message should be sufficient):

and the R-principle corresponds to the receiver’s strategy(the interpretation should imply the message,i.e.,the message should be necessary):

We call the strategy pair(s*,r*)as the max-pragmatic strategy.

In general,the max-pragmatic strategy is not the Bayesian equilibrium ofSG,because the pair of the numbers that maximizes with respect toAandBseparately does not equal the pair that maximizes with respect toA×B.The following proposition provides the sufficient condition for the connection between these two concepts.

Proposition 3.(m*,a*)=(s*,r*)if the following holds.For each ti ∈T,

in which ?represents the Cartesian product.

Intuitively,if the players’strategies maximizing the similarity measure with respect to the state,signal pair and the signal,act pair separately are the same strategies that maximize the utility function inSG,then the max-paragamatic strategy is the same as the Bayesian equilibrium strategy in theSGgame.

Conceptually,Proposition 3 shows the potential applications of ourSGgame in pragmatics.It provides a pragmatic explanation for the Bayesian equilibrium inSGgame.Moreover,in contrast with the Bayesian Equilibrium,the max-pragmatic strategy is easier to calculate.Thus,Proposition 3 provides a simple way to test and find the Bayesian Equilibrium through the max-pragmatic strategy.

6 Discussion and Conclusion

By constructing the signaling game with propositional logic,we demonstrate that the signals in the game can have pre-assumed propositional contents.By considering a new utility function,the players in the game not only consider the outcome of the information transactions but also take into account the language in use.The choice of the set of signals may affect the payoff of the game as well as the optimal strategies of the game.

In addition,the game has the potential to be extended to various directions.We mention two possibilities here.

1.Dynamic context and dynamic meaning

The context of communication and meaning of words change all the time.It would be useful if the current model can deal with the revision of the content of a context and meaning of words.We use the revision operator from Dalal’s model on knowledge base revision ([4]),which follows two basic principles:(1)Primacy of new information:the revised knowledge should conform to the new information;(2)Persistence of old knowledge:as much old knowledge as possible should be retained in the revised knowledge,which means the revised knowledge base is obtained by some form of minimal change.

The basic idea of the revision operator°inα°βis first to extend the models ofαinI(α)by adding or deleting at most one atom for all the elements inI(α),then to take the intersection of the modifiedI(α)(denoted asI1(α))with the new elementI(β).If there is no intersection,then repeat the process onI1(α),until the intersection is not empty.

For example,supposeα：{p,?q},β：{q}.ThenI(α)={p}.I1(α)={?,{p},{p,q}},I(β)={{q},{p,q}}.Thus,I1(α)∩I(β)={p,q}.Therefore,α°βis the formula where its only model is{p,q}.

Applying this revision operation,we can calculate the similarity relation between the revised new formula and the context.For instance,we can calculateE(T,α°β)when the meaning of the word changes orE(T °β,α)when the state of the world changes.

2.Negation and conflictsAs we know when there is a conflict for anyXandY,E(X,Y)=0.Thus,the similarity measurement alone is not enough to capture the intuition in language communication.A conflict measurement can be combined with the similarity measurement to deal with the degree of conflicts between formulas.Such a measurement is already stated in the work in [10].The degree of conflictC(X,Y)betweenXandYis defined as:

In this formula,Distance(X,Y)represents all the hamming distance between the models ofXandY,and is defined in the following way.

LetXbe a set of formulas and letwi,wj ∈I(X).ThenDistance(X,Y)={Dalal(wx,wy)|wx ∈M(X,X ∪Y)andwy ∈M(Y,X ∪Y)}whereDalal(wi,wj)=|wi -wj|+|wj -wi|.The Dalal distance betweenwiandwj,denotedDalal(wi,wj),is the difference in the number of atoms assigned true.