Hao Zhu(朱浩) Shou-Gen Yin(印壽根) and Wu-Ming Liu(劉伍明)

1Key Laboratory of Display Materials and Photoelectric Devices(Ministry of Education),Tianjin Key Laboratory for Photoelectric Materials and Devices,School of Materials Science and Engineering,Tianjin University of Technology,Tianjin 300384,China

2Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

3School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

4Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: vortex chain,anisotropic spin–orbit coupling,magnetic field,Bose–Einstein condensates

1. Introduction

Vortices, vortex chains and vortex lattices have constituted the most relevant topological nontrivial excitations in the condensed matter physics.[1–3]These topological excitations contain phase singularities in the phase field,which can be characterized by winding numbers.[4–6]Usually, vortices are relevant to the external rotation of fluid, i.e., water[7]or superfluid.[8]Vortices have already been predicted or realized in the superfluid phase of4He.[9–11]Remarkably, vortices are opined to be the key point to some foundations of the systems, such as magnetic materials,[12–14]quantum memories,[15–17]and quantum optics.[18–20]Among the plethora of several physical systems, the highly controllable ultracold bosonic gases open a new gate of engineering nontrivial excitations.[21]Therefore, substantial investigations on the vortex generation,[22]the dynamic evolution[23]and the stability[24]have been executed in the field of Bose–Einstein condensations (BECs). To investigate the quantum vortices and superfluidity in the spinor BECs, external rotation often plays an important role.[25]In physics, rotation can be characterized by nonzero canonical angular momentum〈Lcz〉=Ψ?(r× ?p)Ψdr.[26–29]And vortices are generated in response to the canonical angular momentum.[28,29]The common ways to rotate the condensates, including stirring the condensate[30]or rotating the anisotropic trap,[31]could introduce canonical angular momentum. However, with the help of gauge field and magnetic field, nonzero canonical angular momentum can also be generated.[28]

Recent investigations on artificial gauge field, i.e., spin–orbit coupling (SOC) techniques[32–34]in spinor BECs have attracted tremendous interest in systematically studying the novel vortex structures hosted by spinor BECs. For example, Xuet al. have found that Rashba-type SOC could trigger a one-dimensional(1D)vortex chain in spin-1/2 BECs.[35]The anisotropic SO-coupled BECs were firstly discussed by Stanescuet al.,[36]and the ground-state phase diagrams are found to have much richer structures than those obtained by using external rotation.[37]In spin-2 BECs, anisotropic SOC can be used to generate various patterns in the cyclic phase.[38]Furthermore, it is interesting to explore how SOC could generate novel vortex configurations other than the SOC itself.[39]Accompanied by the Ioffe–Pritchard (IP) magnetic field, Dresselhaus-type SOC could trigger vortex lattices in spin-1/2 BECs without external rotation.[28]Various nontrivial excitations, i.e., strip phase and vortex-ring phase, have been investigated with the combined effects of rotation,magnetic field or isotropic SOC in the low-spin systems.[40,41]However,the exotic vortex configurations in the ferromagnetic phase,anti-ferromagnetic phase or the cyclic phase of the spin-2 BECs system remain unclear.

In this paper,we apply anisotropic SOC to trigger 1D vortex chain in the spin-2 BECs. Magnetic field and anisotropic SOC are applied to replace the external rotation, introducing angular momentum to the system. When magnetic field is absent,the 1D SOC(along thex-direction)can induce the plane wave phase ground state. However,thex-axis distributed vortex chain is generated by the combined effect of 1D SOC and magnetic field. Through calculating the particle current and the momentum distribution, we find that the 1D vortex chain is formed attributing to two contrary-propagated plane waves.Through changing the magnetic field, the vortex number inside of the vortex chain is varied. When keep they-direction SOC zero,the vortex number inside of the vortex chain would increase with thex-direction SOC strength. However, when keep thex-direction SOC strength at a fixed value,vortex lattices andy-axis distributed vortex chains can be generated by increasing they-direction SOC strength. Moreover, the influence of the spin-exchange interaction and the spin singletpairing interaction of the vortex chain and the vortex lattice is investigated.

This paper is organized as follows. We firstly introduce the model Hamiltonian in Section 2. The mean-field ground state solution of thex-axis distributed vortex chain is obtained by numerical minimizing the Hamiltonian function, and the particle current and momentum distribution of the vortex chain are discussed in Subsection 3.1. The influence of magnetic field on the vortex chain is discussed in Subsection 3.2. Moreover,we investigate the influence of anisotropic SOC effect on the vortex chain in Subsection 3.3.To connect with real experiments,we discuss the atomic interaction effect on the vortex chain and the lattice in Subsection 3.4. Eventually, Section 4 is devoted to concluding remarks.

2. Gross–Pitaevskii eqnarray

We consider a two-dimensional (2D) spin-2 BECs with the combined effect of anisotropic SOC and IP magnetic field.The mean-field Hamiltonian can be depicted as[42–44]

F=(Fx,Fy,Fz)=(Ψ??FxΨ,Ψ??FyΨ,Ψ??FzΨ) with spin-2 matrices ?Fx,y,z,andΘ=c2(2ψ2ψ-2-ψ1ψ-1+ψ20)/5 is the amplitude of the spin singlet-pair. The anisotropic SOC term can be characterized asVSO=-iˉh(κxFx??x+κyFy??y), whereκxandκyare SOC strength in thexandydirections.[46]The external IP magnetic field is depicted asB(r)=B(x?x-y?y),whereBis the radial field gradient in thex–yplane,and ?x,?yare the unit vectors along thex,ydirections, respectively.[47]For numerical calculation, it is convenient to make the following parameter transformations:

In order to quantitatively discuss the vortex solution,the coupled GP Eqs. (3)–(5) are solved by Crank–Nicolson method.[48]We have verified the stationary state solutions by starting the calculation from a variety of initial conditions,such as the Gaussian-like functions(Ψl～exp[-(x2+y2)/αl]withl=±2,±1,0 andαlrepresenting the width).

3. Results and discussion

3.1. Formation of the vortex chain

We firstly investigate the ground state in the ferromagnetic phase of spin-2 BECs with anisotropic SOCκx=1 andκy=0. Anisotropic SOC strength is fixed and IP magnetic field is not considered(B=0).As shown in the 2D density distribution of Fig.1(a),the rotation symmetry of the condensates is maintained and no density hole emerges because of the SOC effect.As depicted in the phase field of Fig.1(b),the phases of different components change from-π →+π →-π···periodically.Obviously,anisotropic SOC could generate the plane wave ground state, which is similar to the Rashba-type SOC case.[49]No topological nontrivial excitations are generated with pure 1D SOC, while one kind of topological nontrivial excitation is triggered with the combined effect of 1D SOC and magnetic field. As shown in the 2D density distribution of Fig.1(c),we can observe several density holes along thexaxis that are separated by density domains.The vortices can be identified in the phase image of every component of the BECs.From the phase field of Fig.1(d),there are some phase singularities distributing along thex-axis and completely across the whole BECs. This new interesting configuration is referred to as the vortex chain,which essentially differs from the symmetric and equal distribution of vortices in the rotating BECs.[50]In they ＞0 region, there is a plane wave propagated toward the-xdirection. However,in they ＜0 region,there is a plane wave propagated toward the+xdirection. Apparently, thexaxis distributed phase singularities are attributed to the two contrary-propagated plane waves. The 1D vortex chain has been generated by SOC and rotation in the spin-1 BECs,[46]in which rotation could introduce canonical angular momentum to the system. However, the magnetic field in this calculation can work as “rotation” to introduce angular momentum when anisotropic SOC is considered(the effective rotation in the system depends on the gauge potential induced effective magnetic flux).[28]

We can gain further insight into the discussed vortex chain solution by computing the canonical particle current density of the condensate[28]

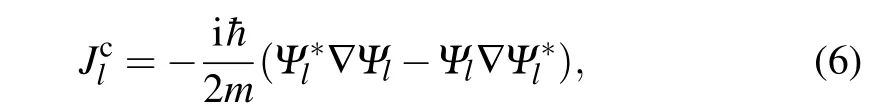
wherel=±2,±1,0 andmrepresents the atom mass. For the anisotropic SOC coupled BECs(κx=1 andκy=0)without magnetic field (B=0), we display the canonical particle current ofΨ-2component in Fig.2(a)(the canonical particle currents ofΨ2,1,0,-1components share the similar configuration). Coincide with the phase field of different components in Fig. 1(b), the canonical particle currentJc-2propagates toward the+xdirection,indicating the plane wave ground state.Additionally, when magnetic field is considered (B=0.25),anisotropic SOC could generate the vortex chain structure(κx=1 andκy=0), and the corresponding canonical particle current ofΨ-2component is exhibited in Fig.2(b). Along with the phase field in Fig.1(d),the condensates are rotated by magnetic field, which results in the anticlockwise circulation of canonical particle current along thex-axis.

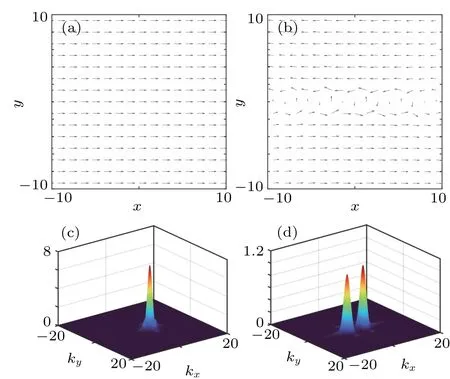
Fig. 2. The particle current and atomic momentum distribution of |Ψ-2|2 component. (a) The particle current of the plane wave phase ground state with magnetic field strength B=0, anisotropic SOC strength κx =1 and κy = 0. (b) The particle current of the vortex chain with magnetic field strength B=0.25, anisotropic SOC strength κx =1 and κy =0. (c) The atomic momentum distribution of|Ψ-2(k)|2 with B=0,κx=1 and κy=0.(d)The atomic momentum distribution of|Ψ-2(k)|2 with B=0.25, κx =1 and κy=0. In the GP simulation,the dimensionless density–density interaction c0=2500,the spin-exchange interaction c1=-50,and the spin singletpairing c2=200. Here,the length of the harmonic trap is ξ0=hˉ/(mω⊥).

In another vein, to better understand the physical meaning of the vortex chain, we transform the density profile of|Ψ-2(r)|2into the momentum space|Ψ-2(k)|2through Fourier transformation,as shown in Figs.2(c)and 2(d). When anisotropic SOC strengthκx=1,κy=0 and magnetic field strengthB= 0, there is one localized Gaussian-type wave package distributing atx ＞0 region, indicating a plane wave propagating toward the+xdirection(Fig.2(c)). On the other hand,when anisotropic SOC strengthκx=1,κy=0 and magnetic field strengthB=0.25,there are two localized Gaussiantype wave packages symmetrically distributing at both sides of they-axis, implying two plane waves propagating toward the+xand-xdirections,respectively(see Fig.2(d)).

3.2. The vortex chain influenced by magnetic field

We next investigate the influence of the magnetic field on the vortex chain when anisotropic SOC is fixed asκx=1 andκy=0. As shown in Fig. 3(a), when magnetic field strengthB=0, different components exhibits Gaussian-type distribution without any density minimum. Meanwhile, the different components with opposite magnetic number (Ψ+2andΨ-2,Ψ+1andΨ-1)are totally overlapped,indicating zero magnetization. When magnetic field strengthB=0.25,thex-axis distributed vortex chain is formed,as depicted in Fig.3(b). Different components are divided into continuous wave packages,and the different components with opposite magnetic quantum number are separated along thex-axis,indicating nonzero magnetization. In the 1D density profile, the density minima correspond to the position of the phase singularities exhibited in Fig. 1(d). The vortices continuously and homogeneously distribute along thex-axis, so we are willing to treat them as a whole vortex chain. Furthermore, the number of vortices in the vortex chain decreases with the strengthen of magnetic field. As shown in Figs.3(c)and 3(d),the numbers of density minima in different components are decreased when magnetic field strengthB=0.5 and 0.75, respectively. We should notice that the number of vortices in a vortex chain is finite and intrinsic at the ground state with SOC and magnetic field. We can artificially change the intrinsic number of vortices inside the chain with different magnetic field strengths.

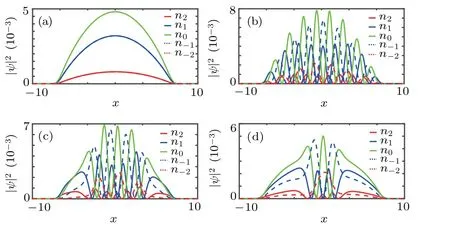
Fig. 3. Effect of magnetic field on the vortex chain in the anisotropic SO coupled BECs. (a) The 1D density profile of different components with magnetic field strength B=0,anisotropic SOC strength κx=1 and κy=0.(b) The 1D density profile of different components with B=0.25, κx =1 and κy=0.(c)The 1D density profile of different components with B=0.5,κx = 1 and κy = 0. (d) The 1D density profile of different components with B=0.75, κx =1 and κy =0. In the GP simulation, the dimensionless density–density interaction c0 = 2500, the spin-exchange interaction c1 =-50, and the spin singlet-pairing c2 =200. Here, the length of the harmonic trap is ξ0=hˉ/(mω⊥).

3.3. The vortex chain influenced by anisotropic SOC

Furthermore, evolution of the vortex chain with anisotropic SOC is studied when magnetic field strength is fixed. We investigate the influence of 1D SOC on the vortex chain, which meansκy=0. For the reason that the different components share the similar density,phase field and momentum distribution, we only exhibit the distribution ofΨ-2component for convenience. The momentum distribution ofΨ-2component varies with thex-direction SOC strength, as depicted in Figs. 4(a)–4(d). When SOC strengthκx=0.25,as shown in Fig. 4(a), there are two localized wave packages localizing symmetrically on the both sides of thekx=0 line.The overlap between the two momentum wave packages is obvious,and one vortex can be identified from the corresponding density contour(the vortex core is circled by the blue circular,and the red circular indicates the density domain). When SOC strengthκxvaries from 0.5→1→2 in Figs. 4(b)–4(d), the distance between the two momentum wave packages becomes larger. The two localized momentum wave packages with no overlap corresponds to two plane waves propagated in the+xand the-xdirections. From the corresponding density contours, we can identify anx-axis distributed vortex chain, in which the vortex number increases with SOC strength.

We next investigate the anisotropy of 2D SOC on the vortex chain,withx-direction SOC strength being fixed asκx=1.Wheny-direction SOC strength is changed from 0 to 0.5 in Figs.4(e)and 4(f),there is a small difference in the momentum distribution ofΨ-2component. However, the corresponding density contours indicate the vortex number in the vortex chain decreases with the strengthen ofκy. When the SOC strength is isotropy in Fig.4(g),we can observe four momentum wave packages coupled together,and four vortices arranged in coaxial annular arrays. Whenκy=2 in Fig. 4(h), two localized momentum wave packages are separated on both sides of theky=0 line,corresponding to two plane waves propagating in the+yand the-ydirections. Consequently,the vortex chain distributes along they-axis.

Fig. 4. Effect of anisotropic SOC on the vortex chain in the BECs system with a fixed magnetic field B=0.25. The atomic momentum distribution of Ψ-2 component varies with 1D SOC κx =0.25,κy =0 in(a),κx =0.5,κy =0 in(b),κx =1,κy =0 in(c)and κx =2,κy =0 in(d). The atomic momentum distribution of Ψ-2 component varies with 2D SOC κx=1,κy=0.25 in(e),κx=1,κy=0.5 in(f),κx=1,κy=1 in(g)and κx=1,κy=2 in(h).The contour images correspond to the density distribution ofΨ-2 component.In the GP simulation,the dimensionless density–density interaction c0=2500,the spin-exchange interaction c1=-50,and the spin singlet-pairing c2=200. Here,the length of the harmonic trap is ξ0=hˉ/(mω⊥).

3.4. Effect of atomic interactions

To connect with experiments, atomic interactions concerning magnetic orders should also be considered to influence the vortex chain. In spin-2 BECs, with the internal degree of freedom, atom collision interactions are generally spin dependent,i.e.,the spin-dependent interactions(the spinexchange interactionc1and the spin singlet-pairing interactionc2)determine the phases of the ground states: ferromagnetic (c1＜0 andc2＞0), anti-ferromagnetic (c1＞0 andc2＜0) or the cyclic phase (c1＞0 andc2＞0).[51]When considering anisotropic SOCκx=1 andκy=0 in Figs.5(a)–5(c),the momentum distribution ofΨ-2components share the similar configuration for different phases. However, the density domains are elongated along they-direction in the antiferromagnetic phase or cyclic phase comparing to the density domain in the ferromagnetic phase. When considering SOCκx=1 andκy=1 in Figs.5(d)–5(f),the symmetry of the momentum distribution ofΨ-2components are different for different phases:SO(4)rotational symmetry in the ferromagnetic phase,U(1)global gauge symmetry in the anti-ferromagnetic phase andSO(3) rotational symmetry in the cyclic phase.Consequently, the density contour indicates that the density distribution is influenced by the atomic interaction.When considering anisotropic SOCκx= 1 andκy= 2 in Figs. 5(g)–5(i),the momentum distribution ofΨ-2components share the similar configuration for different phases. However, the density domains are elongated along thex-direction in the antiferromagnetic phase and the cyclic phase comparing to the density domain in the ferromagnetic phase.

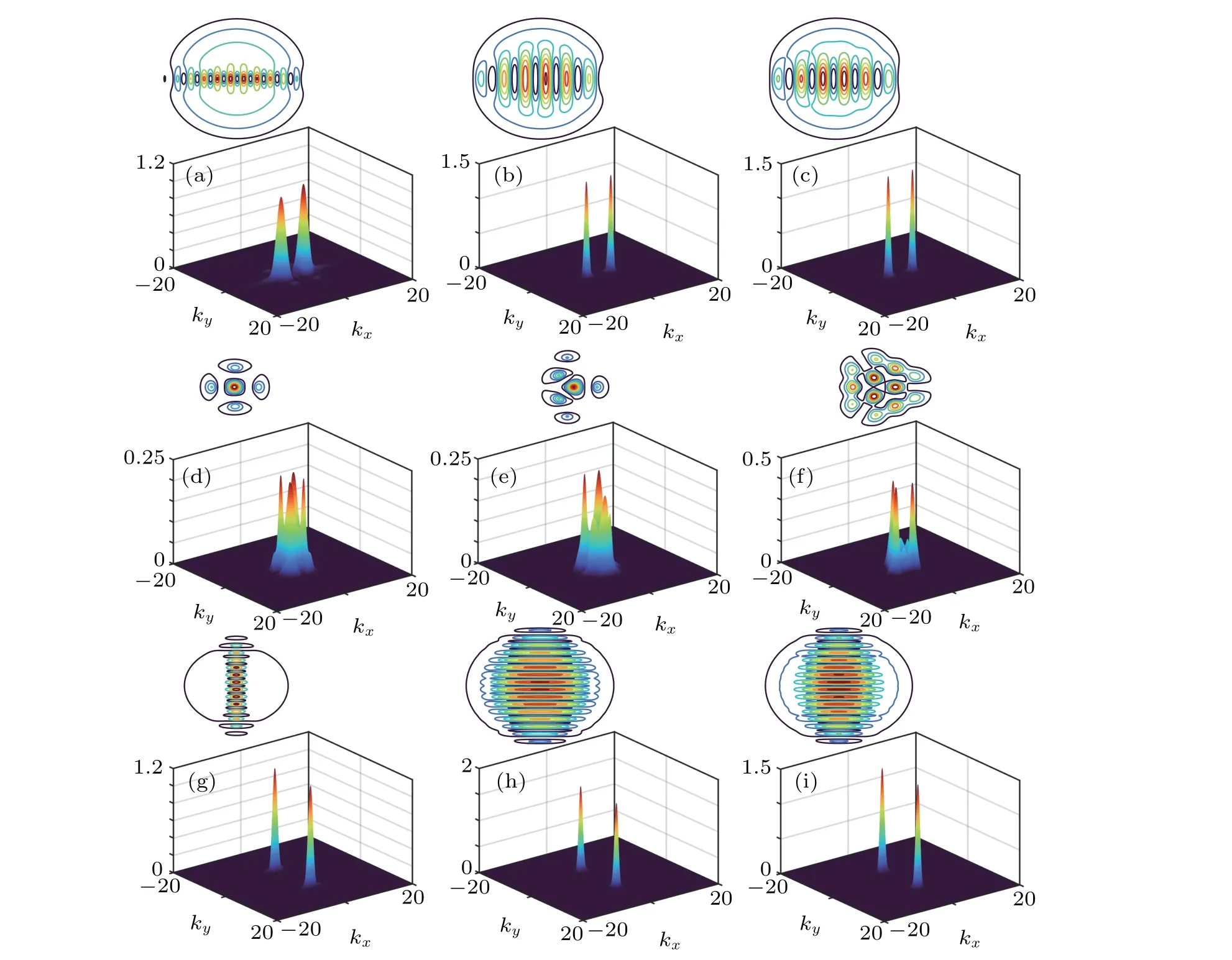
Fig.5. The effect of atomic interaction effects on the vortex chain in the anisotropic SO coupled BECs system with magnetic field. When κx=1,κy=0 and B=0.25, the atomic momentum distribution of Ψ-2 component varies with the spin-exchange interaction and the spin singlet-pairing interaction c1=-50,c2=200 in(a),c1=50,c2=-200 in(b),c1=50,c2=50 in(c). When κx=1,κy=1 and B=0.25,the atomic momentum distribution of Ψ-2 component varies with c1 =-50,c2 =200 in(d),c1 =50,c2 =-200 in(e),c1 =50,c2 =50 in(f). When κx =1,κy =2 and B=0.25,the atomic momentum distribution of Ψ-2 component varies with c1=-50,c2=200 in(g),c1=50,c2=-200 in(h),c1=50,c2=50 in(i). Here,the length of the harmonic trap is ξ0=hˉ/(mω⊥).

4. Conclusion

We have investigated the anisotropic SO coupled spin-2 BECs with magnetic field by solving the coupled GP equations.The 1D vortex chain is generated by the combined effect of 1D SOC and magnetic field. The vortex chain is found to be the consequences of the domain wall of two opposite planewave phases. The magnetic effect mainly affects the number of vortices in the vortex chain.The anisotropy of SOC changes the vortex chain and causes the vortex lattice. Through varying the spin-exchange interaction and the spin singlet-pairing interaction,we find the different density profiles and momentum distributions of the vortex chain or the vortex lattice. This study provides exciting perspectives for nonlinear physics of condensates in artificially induced non-Abelian gauge fields.

Acknowledgments

Project supported by the National Key R&D Program of China (Grant No. 2016YFA0301500), the National Natural Science Foundation of China (Grant Nos. 61835013 and 11971067), Strategic Priority Research Program of the Chinese Academy of Sciences (Grant Nos. XDB01020300 and XDB21030300), Beijing Natural Science Foundation (Grant No.1182009),and Beijing Great Wall Talents Cultivation Program(Grant No.CIT&TCD20180325).