Ning Xi(西寧) and Rong Yu(俞榕)

Department of Physics and Beijing Key Laboratory of Opto-electronic Functional Materials and Micro-nano Devices,Renmin University of China,Beijing 100872,China

Keywords: one-dimensional antiferromagnetism,spin frustration,deconfined quantum critical point,spin dynamics,infinite time-evolving block decimation

1. Introduction

Significant quantum fluctuations in low-dimensional spin frustrated systems can give rise to novel quantum phases and exotic quantum phase transitions.[1–5]One substantial difference from the classical systems is that in these quantum spin systems, some phases can not be characterized by conventional order parameters with broken symmetry. Correspondingly, quantum phase transitions may be beyond the standard Landau–Ginzburg–Wilson (LGW) paradigm. Surprisingly,even when the ordered phases can be described by conventional order parameters with spontaneous symmetry breaking (SSB), the quantum phase transition between them may still be exotic and beyond the LGW paradigm.One of the most attractive examples is the DQCP between the N′eel antiferromagnetic(AFM)and VBS states in two dimensions,proposed by Senthilet al.[6,7]Landau theory dictates a first-order VBS–AFM transition because the order parameters of the two phases break different symmetries. But the theory of DQCP predicts a continuous phase transition between these two phases. At the DQCP, deconfined fractionalized spin excitations emerge and enhanced symmetry allows continuous rotation between the order parameters of the two ordered phases.

The DQCP in two-dimensional (2D) systems has been studied extensively and theoretically.[8–18]Although enormous computational cost are needed to clarify the unusual critical properties and deconfined fractionalized excitation emergent at the DQCP, numerical evidences are cumulated. Currently, most studies are based on several sophisticatedly designed models. To realize a DQCP in realistic 2D spin models or even in experimental quantum magnets[19]is,however,still a challenging task. Recently, some works studied possible DQCP in one-dimensional (1D) spin systems and obtained some interesting results.[20–32]An advantage of the 1D quantum spin systems over their 2D counterparts is that many powerful and well controlled analytical and numerical techniques, such as Bethe-ansatz, bosonization, and density matrix renormalization group (DMRG)[33–35]can be applied,and hence the results are more convincing. Meanwhile, enhanced quantum fluctuations in 1D employ strong constraint to ground-state properties, as involved in the Lieb–Schultz–Mattis (LSM) theorem.[36–38]It is recently noticed that this may help in stabilizing a DQCP in 1D.[26]

For anS=1/2 chain with SO(3)spin rotational and lattice translational symmetries, the LSM theorem[36]implies that the ground state either breaks the translational symmetry to form a VBS or keeps plainly gapless. When generalized to systems with discrete symmetries, this theorem dictates that the ground state can not be symmetric and plainly gapped.Let us consider a system with two distinct discrete symmetries and assume a single tuning parameter can drive the system from one SSB phase to the other. At the transition point the symmetries restore and are often enhanced to allow continuous rotation between the two order parameters. According to the LSM theorem, the ground state at this point must be gapless,and in 1D,this implies the transition point is a DQCP.In many systems,the microscopic Hamiltonian contains such a symmetry-enhanced point by properly tuning the model parameter. For example, theXYmodel consists of an isotropic point with continuous spin U(1)symmetry by tuning the spin anisotropy. Constrained by the LSM theorem, in 1D models,these symmetry-enhanced points exhibit properties that are eligible for a DQCP. This is a special case in 1D, as discussed later in this paper. In another class of systems, the enhanced symmetry can not be explicitly read off from the microscopic Hamiltonian, but emerges as both SSB order parameters are simultaneously suppressed by fluctuations. At the same time,the deconfined fractionalized excitations emerge,making this symmetry-enhanced point a DQCP. This case is more generally discussed in both 1D and 2D.

In this work, we investigate the dynamical signatures of the deconfined fractionalized excitations and enhanced continuous symmetry of two types of DQCP in 1D by studying anS=1/2 spin chain with FM nearest-neighbor and AFM next nearest-neighbor interactions. We calculate the static and dynamic spin correlations by using the time evolution of infinite matrix product states(MPS).We show the existence of emergent continuous symmetries and characteristic of fractionalized excitations at two different DQCPs. At the DQCP between the VBS and FM phases, our calculation of dynamic structure factors suggests there is an effective spin–charge separation. While at the DQCP between theX-direction andZdirection FM phases, we observe two different types of continua associated to different deconfined fractionalized excitations. Our results show direct evidence for the DQCP in 1D and provide valuable information in understanding the nature of the DQCP in both 1D and 2D.

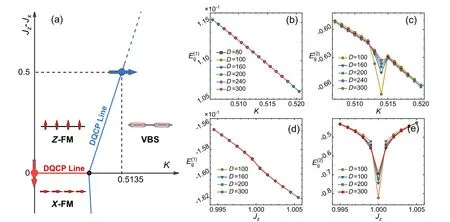
Fig. 1. (a) A schematic phase diagram of the model in Eq. (1). The isotropic line with quasi-long-range (QLR) order (red line) separates the X-direction and Z-direction ferromagnetic(FM)phases,i.e.,a DQCP line. The DQCP line between the FM and VBS phases(blue solid line)with emergent O(2)×O(2)symmetry has been studied in Ref.[20]. A more complete phase diagram is mentioned in Ref.[25]. Here,we just focus on these two deconfined transitions (go through red line or blue line) without examining the properties over the entire phase diagram. (b) The first derivative E(1)g of the ground-state energy with K along the blue arrow in panel(a). (c)The second derivative E(2)g of the ground-state energy with K along the blue arrow in panel(a). (d)and(e)Same to(b)and(c)but along the red arrow.

2. Model and methods

To study the properties of DQCP in 1D, we consider anS=1/2 spin chain with the following Hamiltonian:

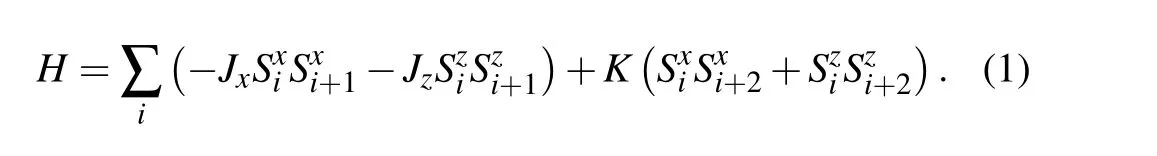
This model has been analyzed by using several different approaches.[20,25,26,30]Reference [30] has numerically confirmed that the ground states include a Luttinger liquid,a VBS phase, and a vector chiral phase sequently by increasingKalong the isotropic line(Jx=Jz). Various field theory descriptions of the DQCPs between the FM and VBS phases have been discussed in detail in Ref.[26]. Another interesting analogy is mentioned in Refs. [26,30] that the VBS phase can be viewed as a symmetry-protected topological (SPT) phase by considering unit cells of two lattice sites. However,this SPTlike phase is obviously topologically trivial when examining the edge mode,given that the VBS is a SSB phase. But for the case of an infinite chain,the edge is unimportant,and therefore this analogy can make senses.

An anisotropic O(4) non-linear sigma model (NLSM)with the Wess–Zumino–Witten term has been proposed to describe the scaling behaviors and emergent symmetry of the DQCP between the FM and VBS phases.[20]Here,to gain further understanding on the symmetry and fractionalized excitations of the two DQCPs, we apply the celebrated Jordan–Wigner(JW)transformation to this spin model and map it into interacting spinless fermions. The Hamiltonian in the fermion representation then reads

TheH0corresponds to the nearest-neighbor term of Eq. (1).The interaction termHintis transformed from the next nearestneighbor term of the spin model. Note that ?Tiis defined“onbond”and ?Niis defined“on-site”.

In this work, we adopt the infinite time-evolving block decimation (iTEBD)[39,40]method to study the ground-state properties and zero-temperature space–time correlations of the spin model defined in Eq.(1). We focus on the critical behaviors near the two transitions as shown in Fig.1(a). The matrix product representation is known to be accurate and efficient for gapped systems when the truncation dimension (Schmidt rank)Dis large enough. In the situation where the system is gapless, the matrix product representation can still be applied and it provides a finite-gap(or finite-entanglement)variational state of a gapless system. With various well developed finite correlation length or finite-Dscaling techniques, MPS representation is capable of exploring the critical properties trustingly.[41–43]

In the iTEBD method, one usually starts from a random initialization. Deep inside an ordered phase, the ground state is not sensitive to the way of initialization. The local order parameters and ground-state energy can be determined sufficiently accurate at a finiteD. However, when the system is close to a critical point,finite-Deffects may appear. There are usually two issues. The first issue is related to the emergent symmetry at the transition.Near the transition point,the emergent symmetry will give rise to many nearly degenerate ground state configurations,which are local minima in the variational approach. To avoid being trapped in a local minimum, our optimization procedure starts with many different initializations and the state with the lowest energy in the optimization is selected as the ground state. As a second issue, the gap obtained in a finite-DMPS is always finite. To solve this problem,we apply the well developed finite entanglement scaling technique,which allows to accurately locate the critical point from extrapolation.

For a state with a finiteD, a finite gap presents because of the finite correlation lengthξ(D). To eliminate the effects of the finite-Dgap to the critical exponents, we adopt a selfconsistent method to determine the critical exponents. Applying the finite correlation length scaling approach, the critical exponents and the scaling function can be obtained from data collapse for differentD’s. We then use the fitted results to do a power-law fitting for the data with the largest correlation length,from which the critical exponents are reestimated.This procedure then repeats until the evaluated exponents are converged. Details of this self-consistent scaling method is elaborated in Appendix B.

The dynamical structure factors are calculated from the Fourier transforms of the space–time correlations. The calculation of space–time correlations is based on the real-time evolution of the ground-state MPS.[44]The computational cost of calculating the space–time correlations is much higher than optimizing a ground state. To keep the balance between truncation error and energy resolution, in this work, we adopt a fourth-order Trotter expansion of the real-time evolution operator,which leads to the energy resolution less than 10-3J.

3. Ground-state phase diagram and symmetries at the DQCPs

The schematic phase diagram of the model defined in Eq. (1) is presented in Fig. 1(a). ForJz ＞Jxand smallKthe ground state is a FM with spin ordered along theSzdirection (denoted as theZ-direction FM). Since the model is symmetric under thex ?zinterchange,the ground state is anX-direction FM forJz ＜Jxand smallK. For sufficiently largeK,the ground state is a VBS that breaks the translational symmetry. TheX-direction andZ-direction FM states meet at the isotropic lineJz=Jxwhere the spin rotational symmetry of the Hamiltonian is enhanced from Zx2×Zz2to U(1). Constrained by the LSM theorem, along this line, the ground state preserves the U(1)symmetry and keeps to be gapless. Across this line from theX-direction FM to theZ-direction FM by tuning the parameterJz-Jxin the model,the system undergoes a continuous transition. At the transition point, the low-energy excitations are described by JW fermions. The JW fermions are deconfined with the enhanced U(1) symmetry, and can be viewed as the fractionalized excitations of domain walls(DWs), just like the marons or instantons for vortex in 2D.Therefore,the phase boundary between theX-andZ-direction FM phases(red line in Fig.1(a))can be regarded as a line of DQCPs.

The transition between theZ-direction FM and VBS phases is driven by the next nearest-neighbor couplingK. It has been proposed that DQCPs with emergent O(2)×O(2)symmetry exist along the FM and VBS phase boundary (the blue line in Fig.1(a)).[20,25,26]To understand the origin of the enhanced continuous symmetry,we examine the system in the JW fermion representation.The transition is controlled byHintin Eq. (4), which contains an “on-bond” term (including ?Ti)and an “on-site” term (including ?Ni). Relevance of the “onbond”term will cause breaking the translational symmetry on bonds and preserving all on-site symmetries, and therefore form a VBS. By contrast, the relevance of the on-site term will cause breaking the translational symmetry on sites and preserving all on-bond symmetries. This would result in aYdirection AFM phase. For sufficiently largeKin this model,the ground state prefers to a VBS instead of aY-AFM state.In the continuous limit,these two terms ofHintcorrespond to the same order of interaction but pinning down different ordered states. There are also two sets of rotational symmetries originated from the on-bond and on-site symmetries, respectively. Interestingly, with proper tuning, the on-bond and onsite terms can be simultaneously marginal, which cause the enhanced O(2)×O(2) symmetry. Note that these emergent continuous symmetries at the transition is not possessed by the microscopic Hamiltonian of Eq. (1). This is a key difference from the transition across the boundary of the two FM phases. However, due to the LSM theorem in 1D, they share many similar features,and are both eligible for DQCPs.

4. Critical properties at DQCPs

Fig. 2. (a) The Z-FM order parameter mz and VBS order parameter Ψ versus K at Jz-Jx =0.5. (b) Z-FM order parameter mz and X-FM order parameter mx versus(Jx-Jz)/(Jx+Jz)at K=0. (c)Scaling of the entanglement entropy S with effective correlation length ξ. The central charge is extracted from the slope of a linear fit.

Figures 1(d)and 1(e)show the derivatives of ground-state energy across theX-FM toZ-FM transition. The results are similar to those in Figs. 1(b) and 1(c). Meanwhile, the order parameters of the two SSB phases,mzandmx, both drop down to zero at the transition point simultaneously,as shown in Fig. 2(b). These results evidence a continuous transition,and imply that the symmetry is enhanced to U(1) at the transition point, which is consistent with the LSM theorem. Besides the similar behaviors in the order parameters, we find the central charges of the two transitions are both close to 1(see Fig. 2(c)), which belong to the free boson universality class.[45,46]This does not mean the low-energy excitations are bosonic, but implies that they arise from fractionalizing the bosonic modes,which is a feature of DQCP.

To further show the two transitions are eligible for DQCPs, we further calculate the correlation functions to verify the existence of emergent continuous symmetry and global topological conservation. The gauge constraint at the DQCPs guarantees the conservation of the Noether current,?μJμ=0,which implies that the anomalous exponents of the conserved currents must be pinned toη=2,and the current–current correlation in energy–momentum space must be gapless and linear.

Table 1. Identification of the vector components and conserved currents for different emergent O(2)symmetries.

The vector components and conserved currents of emergent symmetries are listed in Table 1. For the FM–VBS DQCP,it has been proposed that there are two emergent O(2)symmetries.[20]In the spinon language, the continuous rotation of uniformSxand staggeredSyis the gauge symmetry on site with spin flip and the rotation ofSzand Ψ is the gauge symmetry on bond without spin flip. Thus,we can regard the rotation of uniformSxand staggeredSyas an effective“spin”sector, labeled as O(2)s. On the other hand, the rotation ofSzand Ψ form an effective“charge”sector, labeled as O(2)c.As shown in Figs.3(a)and 3(b),although these two different O(2) symmetries keep different anomalous exponents, their conserved currents both follow a scaling law ofJ～r-2and in each sector(charge or spin)the two vector components behave with the same scaling dimension. Besides,an additional resultηcηs≈1 validates the prediction of field theory in Ref.[20].

Fig.3. Correlation functions of the emergent conserved currents and vector components for(a)O(2)c of the FM–VBS transition,(b)O(2)s of the FM–VBS transition, (c) O(2)s of the X–Z FM transition, and (d) SU(2)c of the X–Z FM transition.

For the transition between the two FM states at the isotropic point withJx=Jz,there is an enhanced U(1)～O(2)symmetry. As demonstrated in Fig. 3(c), the scaling law ofSy～r-2reflects the global conservation of the JW fermion number. It can also be regarded as the conserved current of theX–Zrotation, labeled as O(2)s. To further illustrate the notion of deconfinement, we show that another SU(2)csymmetry listed in Table 1 is also emergent at the DQCP of theX–Ztransition. As demonstrated in Fig. 3(d), the anomalous exponents of these three operators are all pinned at an integer of 2,which indicates an emergent SU(2)symmetry.

5. Dynamical signatures of DQCPs

Results in previous sections only provide evidences for continuous FM–FM and FM–VBS transitions,based on which the DQCPs are implied. To directly show the existence of deconfined fractionalized excitations at the DQCPs, we calculate the space–time correlations of conserved currents and spin components by real-time evolution of the ground-state MPS.After Fourier transforms of the space–time correlations, we can get a dynamical spectrum in the energy–momentum space.

As demonstrated in Figs. 4(a) and 4(b), the current–current correlations in energy–momentum space at the transition points are indeed gapless with linear low-energy dispersion.At the FM–VBS transition,the two emergent symmetries O(2)cand O(2)scan be identified from the“charge”and“spin”channels separately, and they have the same Fermi velocity.Combining these results with the analysis of anomalous exponents above,we can safely confirm that there exist two emergent symmetries. At the DQCP of theX–ZFM transition,Syis the conserved current of theSx–Szrotation as well as of the Φ–Γrotation. The existence of two continuous symmetries at theX–ZFM transition is also confirmed.

The signatures of deconfined fractionalized excitations at the FM–VBS DQCP are illustrated in Fig. 5 clearly. Approaching to the DQCP from either side,we observe the development of two sets of continuous spectra(panels in the upper and lower rows of Fig. 5). As shown in Figs. 5(b) and 5(e),they both become gapless at the DQCP.Near the zone center,these two continua are bounded by the same edge (linear in the momentumk). However,when going away from the zone center by increasingk, they are separated with two independent edges. Note that these two modes are associated with effective“charge”and“spin”channels,respectively. Therefore,this is the signature of an effective spin–charge separation of the system. The spin–charge separation is common in 1D Luttinger liquid. In the long wave length limit, the interaction terms causing charge(VBS)and magnetic(Z-FM)orders are all irrelevant under renormalization group (RG) flow, which signifies free fermion excitations. However, as the momentumkincreases, the effect of the scattering processes lead to the separation of spin and charge excitations. In the case of the easy-plane DQCP in 2D proposed by Senthilet al., the spinons(fractions ofS+)and merons(fractions of skyrmions)are deconfined simultaneously,in a way analogous to the spin and charge excitations discussed here.

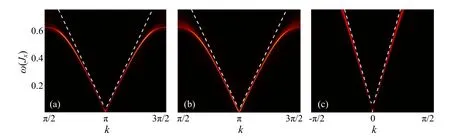
Fig.4. Low-energy spectra of the dynamic current–current correlations listed in Table 1. (a)–(c)Correlations of Jc at the FM–VBS transition,Js at the FM–VBS transition and Sy at the X–Z FM transition,respectively. The white lines are fits to the linear dispersion.

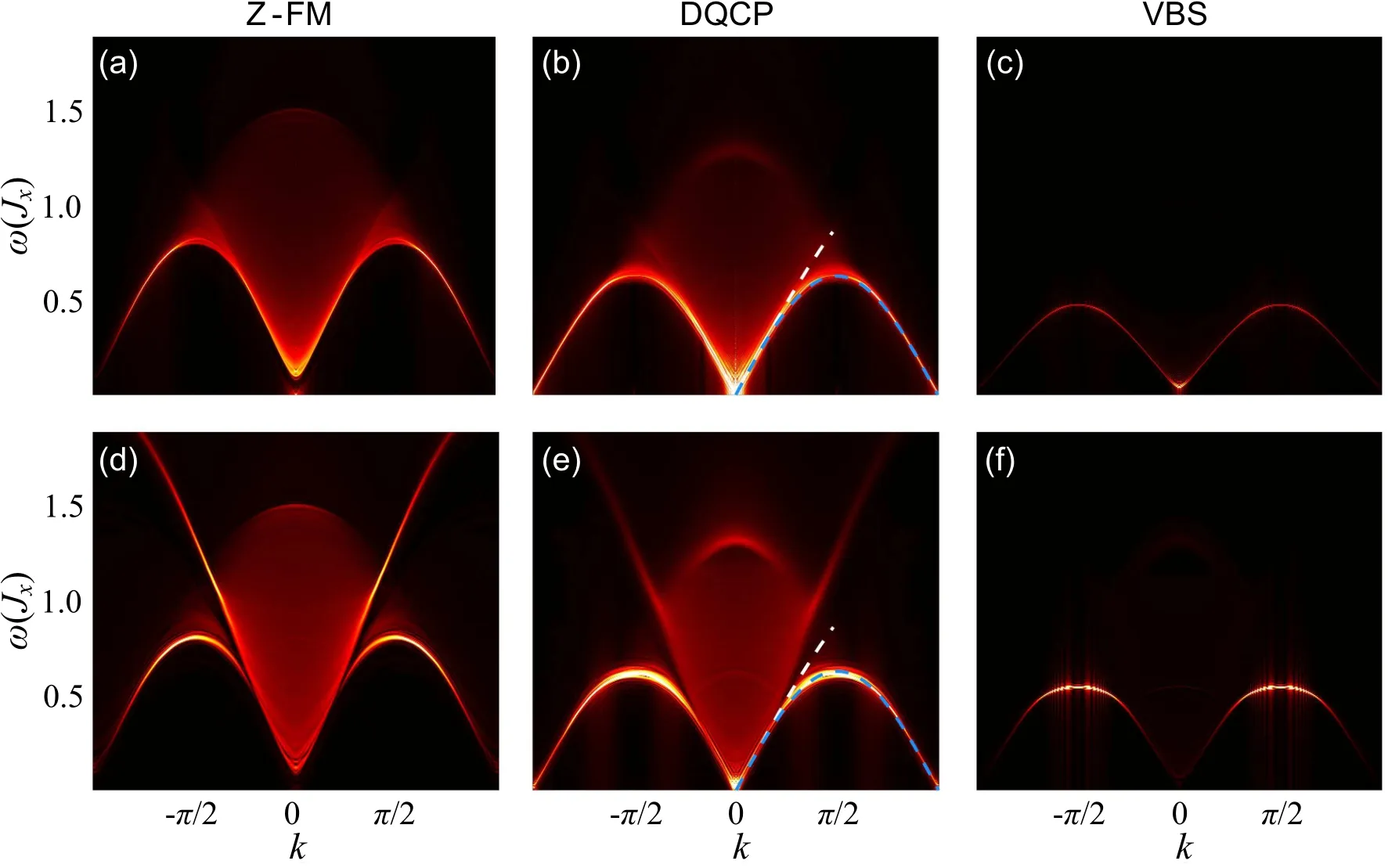
Fig.5. Dynamic spin structure factors of(a)–(c)the Sz channel and(d)–(f)the Sx chanel. Panels(a)and(d)are inside the Z-FM phase. Panels(b)and(e)are at the DQCP.Panels(c)and(f)are inside the VBS phase. The blue and white dashed lines in(b)and(e)trace out the two bright bound edges from(b)and are guides to eyes in(e).

The excitations at theX–ZFM DQCP are clearer. The continuum showed in Fig. 6(a) is conspicuous with clear boundaries. In the JW fermion representation,it is nothing but the particle–hole excitations of the free fermions. The topological excitations(JW particles)are totally deconfined at any length scale. The clear boundary is the sign of a well defined Fermi surface. The continuum of theSxSzchannel in Fig.6(c)can also be regarded as a measure of the topological excitations and it is a folding of the continuum in Fig. 6(a). In theSx(orSz)channel,the gapless point of the continuum appears atk=0 and the boundary of the continuum is indistinct as demonstrated in Fig.6(b), which is different from the behavior in theSychannel. The excitation spectrum shown in theSx/zchannel suggests a Dirac cone like Fermi surface. At a first glance this is surprising because the model at this point is mapped to non-interacting JW fermions. However,we note that the JW transformation itself is nonlocal,and theSx/zchannel just happens to probe the inherent many-body effects.This is a unique feature of 1D systems.

The anomalous exponents ofSx,Sy, andSxSzhave been calculated in the previous section. Differentηvalues are also characterized in the dynamical structure factors. Forη=0,the excitation spectrum would contain a bright bound state.Forη=1,which corresponds to the free JW fermions,[35]the spectrum should exhibit a smooth continuum just like the one shown in Fig. 6(a). And forη=2, at a fixed momentumk,the spectral weight will vanish atω=0 and increase linearly with the frequencyω,just like the continuum neark=±πin Fig.6(c). For the correlations ofSx,η=0.5. The dynamical structure factor of this channel,as shown in Fig.6(b),exhibits a continuum with a bright edge, consisting of characters of excitations at bothη=0 andη=1.

Fig.6. Dynamic structure factors of(a)Sy channel,(b)Sx channel,and(c)SxSz channel at the DQCP of the X–Z FM transition.

6. Discussion and conclusions

As mentioned in the introduction, the realization of a DQCP in 2D spin systems without fine-tuning is still challenging and the enormous computational cost limits detailed analysis of the critical properties,especially the dynamical ones.As a reasonable instead,we numerically study the critical properties of 1D DQCPs in detail. We show that the model in Eq.(1)contains two types of DQCPs,which are located at the VBS–FM and theX–ZFM transitions, respectively. They share many similar critical properties that are eligible for DQCPs,despite the different underlying mechanisms and symmetry aspects. These key differences are clearly reflected in the calculated dynamic spectra of different spin channels, which are firstly explored in this work. The gapless and linear dispersions of the current–current correlations in energy–momentum space further verify the existence of emergent symmetries. At the VBS–FM DQCP,our calculation of dynamic spin structure factors give robust evidence of spin-charge separation. And at theX–ZFM DQCP, besides the JW fermion continuum, another type of fractionalized excitation is observed.

In the field theory description,these two different types of DQCPs can both be described by the same low-energy effective model — the sine-Gordon model,[47]although their microscopic Hamiltonians’ symmetries are totally different. In this sense,the ground states exactly on these two lines both exhibit Luttinger liquid behavior at low energies. As expounded in Section 5,the low-energy excitations for these two DQCPs do not show notable difference, qualitatively. On the other hand,the spin–charge separation takes place at higher energy and larger momentum,for which the dispersions show distinct nonlinear behavior and hence beyond the field theory description. There are also other additional modes for the FM–VBS DQCPs at much higher energy. It would come as no surprise because this energy scale is far beyond the field theory capability and thus the different symmetries embodied in microscopic Hamiltonians will lead to different excitation modes.Nevertheless, the different excitation modes at higher energy may contain some interesting consequences beyond the lowenergy view at present and it would inspire us to develop more analytical approaches for larger energy scale.

Our results also verify the important role of the LSM theorem played in stabilizing the 1D DQCP. At the transition point between theX-FM andZ-FM phases, the symmetry of the Hamiltonian is enhanced to U(1).Constrained by the LSM theorem, the ground state at this point should preserve the symmetry and be gapless. Although LSM theorem does not rule out a first-order transition between the two SSB phases in general, the unique feature of 1D system excludes the possibility of a Goldstone mode. Therefore,a first-order transition with an enhanced continuous symmetry can not take place in 1D, and the system must undergoes a continuous transition,namely, via a DQCP. As discussed, this type of DQCP can only be realized in 1D systems. In higher dimensions, emergent Goldstone mode associated with the enhanced symmetry appears and the transition is usually of first order. On the other hand, the enhanced continuous symmetry at the DQCP between the FM and VBS phases emerges only in the long wave length. This type of DQCP is not limited in 1D.

In summary,using the iTEBD method,we study the critical properties as well as the dynamical spectra of two types of 1D DQCP in anS=1/2 spin chain. The scaling of the correlation functions and the dispersion of the conserved current correlations explicitly show the emergence of enhanced continuous symmetries at the two different DQCPs. The dynamical signatures of the spin excitation spectra reveal deconfined fractionalized excitations at the DQCPs.We also find an effective spin–charge separation at the DQCP between the the FM and VBS phases, and identify two continua associated with different types of fractionalized excitations at the DQCP between theX-direction andZ-direction FM phases. Our results uncover rich physics of the DQCP in 1D and help understand the nature of DQCP in higher dimensions.

Appendix A:Some useful Lie algebras

Here we summarize some local Lie algebras in Table A1.They are useful in defining the order parameters and when approaching to a DQCP,global topological conservation laws arise. The on-site spin SU(2)algebra is obvious and denoted as SU(2)sin Table A1. Besides, there are also two sets of on-bond algebras. There are four basis states in a two-site unit cell,(|↑↑〉,|↓↓〉,|↑↓〉,|↓↑〉),and we can separate them into two parts, (|↑↑〉,|↓↓〉) and (|↑↓〉,|↓↑〉), for which the numbers of domain walls (dw) contained are 0 and 1, respectively. The operatorsναi,j(α=1,2,3) defined in Table A1 form a closed SU(2) Lie algebra in the dw = 0 space (|↑↑〉,|↓↓〉), and is therefore denoted as SU(2)dw0. While the operatorsταi,jalso form a closed SU(2)algebra in the dw=1 space,which is denoted as SU(2)dw1. All these operators listed in Table A1 can not mix the spaces between dw=0 and dw=1,namely,they preserve the number of domain walls locally.

Table A1. Related SU(2)Lie algebras in this work.

Appendix B:Finite entanglement scaling

For a matrix product state with a finiteD, the finite gap is associated to a finite effective correlation lengthξ(D). This effective correlation length can be calculated from the correlation structures of the MPS.The static correlation of two operatorsuandvin the MPS language reads[40]

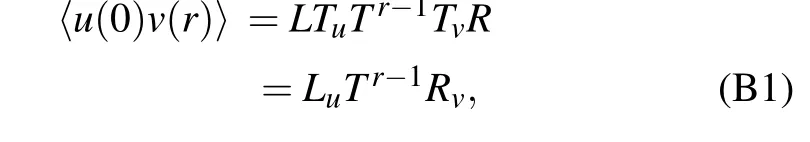
whereTis the transfer operator,LandRare the left and right eigenvectors ofTwith the largest eigenvalue, respectively.This process can be expressed in a more intelligible tensorgraph representation as demonstrated in Fig.B1.

Fig.B1. Graph representation of two-point correlators.

Typically, the transfer operatorTis a symmetric matrix(corresponding to the space-inversion symmetry) and it can be diagonalized with real eigenvalues. Two-point correlators〈u(0)v(r)〉can be transformed as follows:

whereηis the anomalous exponent andf(r/ξ)is a homogeneous scaling function. For the matrix product representation,the exponential decay factor exists all along even in a gapless state.Even so,close to the transition point,the power-law term will dominate the scaling behavior of the correlation function forr ＜ξ.

Fig.B2. Self-consistent process to extract the anomalous exponents.

Data collapse has been widely adopted to extract the anomalous exponents. However, it is often hard to judge the quality of data collapse. So it usually only provides some rough estimate of the exponents. Alternatively, one can also extract the anomalous exponents from a direct power-law fit to the correlation functions.However,there are some practical issues for a direct fit because the sub-leading contribution in the scaling functionf(r/ξ)would have an effect on the accuracy of fitting for the short-range correlations and the exponential decay factor would ruin the power-law behavior of the longrange correlations. Here we adopt a way to extract the exponents by combining these two methods,and show that this will give refined estimates of the anomalous exponents. Specifically, direct power-law fitting can provide an initial value of the anomalous exponentη, andf(r/ξ) fitted from data collapse can be used to promote the power-law fitting of the correlation function. This process is then repeated until a self consistence ofηis obtained. The sketch of our method is illustrated in Fig.B2. The final fitting results of the anomalous exponents are illustrated in Fig.3 of the main text. Examples of data collapse forGxat theX–ZFM transition andGΨat the FM–VBS transition are shown in Fig.B3,respectively.

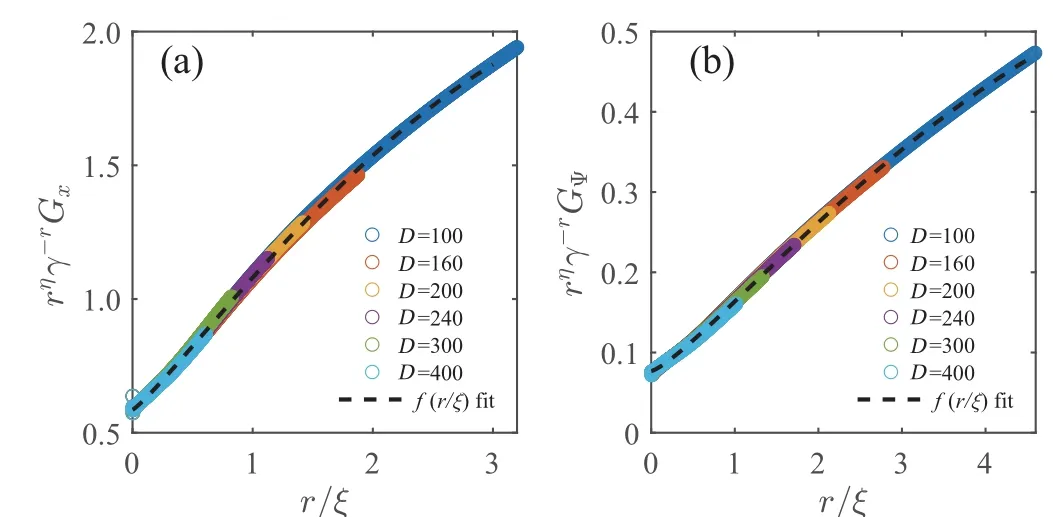
Fig.B3.Data collapse of the correlations functions for(a)Sx at the X–Z FM transition and(b)Ψ at the FM–VBS transition.

Appendix C: Calculation of dynamic structure factors

To trace out the low-energy linear dispersion in thek–ωspace,we find out theωvalues corresponding to the maximum of DSF for eachkand then fit thek–ωdata nearby the zoom center linearly. The linear guide lines in the main text are our linear-fitting results in this way and the boundary guide lines are direct plots ofk–ωdata.

Acknowledgments

We thank Z.Y.Xie,Z.X.Liu,W.Q.Yu,Y.Wang,J.Wu,and C.L.Liu for useful discussions.

Project supported by the National Science Foundation of China (Grant No. 12174441), the Fundamental Research Funds for the Central Universities, China, and the Research Funds of Remnin University of China (Grant No.18XNLG24).