Xiao-Zhe Li?Qing-Xian Zhang?He-Yi Tan?Zhi-Qiang Cheng?Liang-Quan Ge?Guo-Qiang Zeng?Wan-Chang Lai

Abstract The rapid identification of radioactive substances in public areas is crucial.However,traditional nuclide identification methods only consider information regarding the full energy peaks of the gamma-ray spectrum and require long recording times,which lead to long response times.In this paper,a novel identification method using the event mode sequence(EMS)information of target radionuclides is proposed.The EMS of a target radionuclide and natural background radiation were established as two different probabilistic models and a decision function based on Bayesian inference and sequential testing was constructed.The proposed detection scheme individually processes each photon.When a photon is detected and accepted,the corresponding posterior probability distribution parameters are estimated using Bayesian inference and the decision function is updated.Then,value of the decision function is compared to preset detection thresholds to obtain a detection result.Experiments on different target radionuclides(137Cs and 60Co)were performed.The count rates of the regions of interest(ROI)in the backgrounds between[651,671],[1154,1186],and[1310,1350]keV were 2.35,5.14,and 0.57 CPS,respectively.The experimental results demonstrate that the average detection time was 6.0 s for 60Co(with an activity of 80400 Bq)at a distance of 60 cm from the detector.The average detection time was 7 s for 137Cs(with an activity of 131000 Bq)at a distance of 90 cm from the detector.The results demonstrate that the proposed method can detect radioactive substances with low activity.

Keywords Natural radiation?Nuclide identification?Sequential testing?Nuclear safety

1 Introduction

Radioactive substances are a threat to public safety when they are present in public areas.In such cases,nuclide identification is crucial for inspecting radioactive substances.Traditional radionuclide identification methods[1,2]are based on the full energy peak information of the gamma-ray spectrum and require that the particle events generated by the decay of nuclides are treated as statistics in the spectrum.Peak-finding algorithms such as the derivative peak searching method,second derivative peak identification method[3],covariance peak-search method[4],and symmetric zero-area peak searching method[5]use full energy peaks information to identify nuclides based on the energy of the gamma rays from nuclides.To obtain a low-statistic spectrum,a long spectrum recording time is required,resulting in a slow response time.To compensate for the shortcomings of traditional radionuclide identification methods,novel detection methods have been proposed,including the adaptive filtering method[6],chaos oscillator method,blind-source separation method,and stochastic resonance method[4].The adaptive filtering method is a weak signal detection method with an optimal parameter adjustment function that was developed based on the Kalman filter.This method can automatically optimize a nuclear signal.For the Chaos oscillator method,a nuclear signal in the form of a periodic signal is superimposed with a fixed-frequency chaotic oscillator.The mixed signal is then detected and processed using phase differences.The blind-source separation method uses an analysis algorithm to obtain the best estimate of a nuclear signal.The stochastic resonance method uses the synergistic effects of noise and signals to analyze nuclear signals.Sullivan adopted wavelet transforms and the modulus maxima method[7,8]to achieve accurate nuclide identification using low-resolution spectra.Several artificial neural network(ANN)methods have also been introduced in previous studies[9–12]based on their significant success in other research fields.Liang used the K-L transform to extract gamma-ray spectrum features and trained an ANN to perform radionuclide identification.Experiments and tests demonstrated that the ANN method is effective for rapid radionuclide identification[12].Furthermore,Yang et al.proposed a radionuclide identification method based on machine learning and pattern recognition[13–18],and Chong Jie and Yi Ming used a fuzzy-logic-based algorithm to discriminate characteristic peaks and identify radionuclides[19–21].Although the aforementioned gamma-ray spectrum analysis methods have proven to be reliable and practical,a long recording time is required to obtain a spectrum with low statistical error.Therefore,these techniques cannot meet the requirements for real-time radionuclide inspection in public areas.

In 1945,Wald proposed the sequential probability ratio testing theory[22],which can be used to perform real-time analysis and judgment regarding whether a hypothesis is true based on recorded events.The results satisfied statistical requirements.The sequential probability ratio test combined with the Bayesian law for posterior probability distributions has been applied in many fields[23,24].Candy proposed a sequential Bayesian radionuclide identification method in 2008.This method combines the sequential probability ratio test and Bayes rule for radiation monitoring and radionuclide identification,and establishes a radiation detection model.In 2010,Candy et al.developed SRaDS,which is a radiation monitoring system using a sequential-Bayesian-based radionuclide identification method[25].SRaDS automatically eliminates irrelevant and unexpected photons during the detection process and improves detection efficiency.This system abandons the concept of the energy spectrum statistics used for traditional nuclide recognition.It uses a Bayesian algorithm to group each target photon,compares preset parameters for each photoelectric event sequence,and calculates the probability of the target radionuclide corresponding to the photoelectric event sequence.Finally,the statistical results of multiple single-energy ray groups are used to determine whether the target radionuclides are detected.This method can successfully detect radionuclides when the number of recorded photons is small and the measurement time is short[25,26].

This method makes full use of event mode sequence(EMS)information.An EMS of the target radionuclide can be treated as a composition of EMSs emitted from several monoenergetic source components.A well-defined probability model can then be used to describe the EMS of the target radionuclide.Therefore,a sequential Bayesian detection scheme can be applied to identify radioactive nuclides in real time by incorporating energy,count rate,and emission ratio information[24,27].Unlike the traditional full-spectrum-analysis-based method,this method can detect radionuclides under low-count conditions.However,the results of this method are affected by the background count and some simulation experiments by Xiang Qingpei verified that it may be inaccurate in cases with high background counts[25,26].

In this study,two different probabilistic models were established based on the EMSs of natural background radiation and target nuclide radiation fields.The posterior distribution parameters of the probabilistic models were then estimated using Bayes’law.Finally,nuclide identification was performed via sequential detection.Once a photon has been detected and processed,the posterior probability distribution parameters can be estimated using Bayesian inference and a decision function can be updated and compared to preset detection thresholds to determine whether the target radionuclide is detected.In this paper,a rapid nuclide identification model and sequential detection scheme are introduced,followed by the presentation of validation experiments on target radionuclides(137Cs and60Co).

2 Methods

2.1 Nuclide identification model based on background comparisons

The concept of monoenergetic decomposition[13]has been proposed to leverage EMS information.Suppose that the sequence of photons emitted by a radionuclide is a set of photons emitted by several separate monoenergetic sources.AnEvent（n;em（n），Δτm（n））is defined as thenth gamma ray recorded by the detector.This ray is emitted by themth monoenergetic source with a measured energyem（n） and interarrival timeΔτm（n） between the current and previous event.The EMS of a target radionuclide(EMSrn)is then represented asEMSrn（N;e，Δτ）.

The indexmrepresents themth monoenergetic source of a target radionuclide and the total number of monoenergetic sources isM.The detector detectsNmevents from themth monoenergetic source during the detection period.is defined as the complete set of energies composingEMSrnalong with,which is the corresponding set of interarrival times.Nis the sum of the setNm.

Considering instrument noise and experimental uncertainty,the measured energy of the gamma rays emitted by a monoenergetic source in a radiation field follows a Gaussian distribution and the interarrival times follow an exponential distribution(based on the Poisson statistics of nuclear decay)[28].The corresponding formula is presented in Eq.(2),wheremandσemare the expected value and standard deviation of the Gaussian distribution,respectively.λmis the expected value of the exponential distribution andαmis the emission probability of themth monoenergetic source.

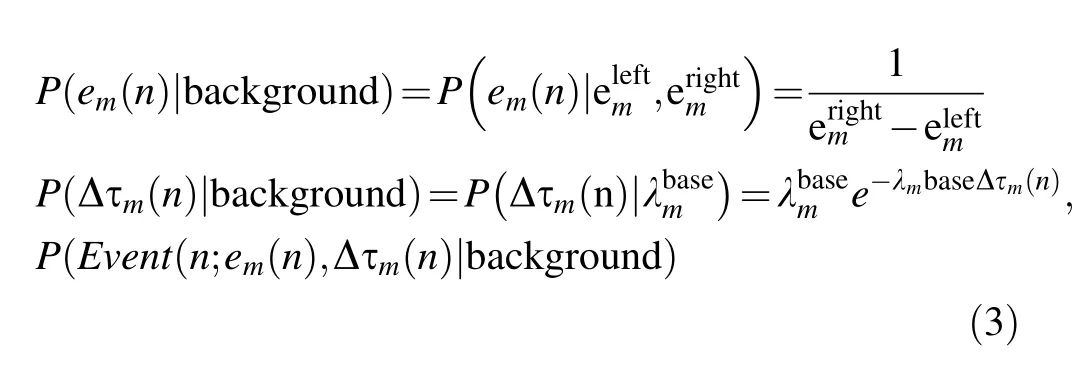
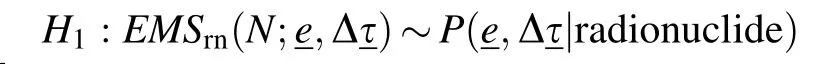
［if radionuclide is detected］,

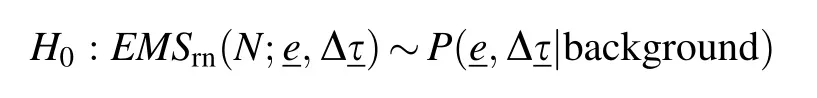
［if radionuclide is not detected］

When a radionuclide is detected,radionuclide）is considered as the probabilistic model of the EMS.Otherwise,the probabilistic model of the EMS isbackground）.The optimal solution to this binary decision problem is provided by the Wald sequential probability ratio test[22].It is assumed that theNth detected photon is emitted from themth monoenergetic source.According to the definition in Eq.(1),there are a total ofNmphotons detected from themth monoenergetic source and the likelihood ratioRatio （N）is obtained by applying the Newman–Pearson theorem as follows:

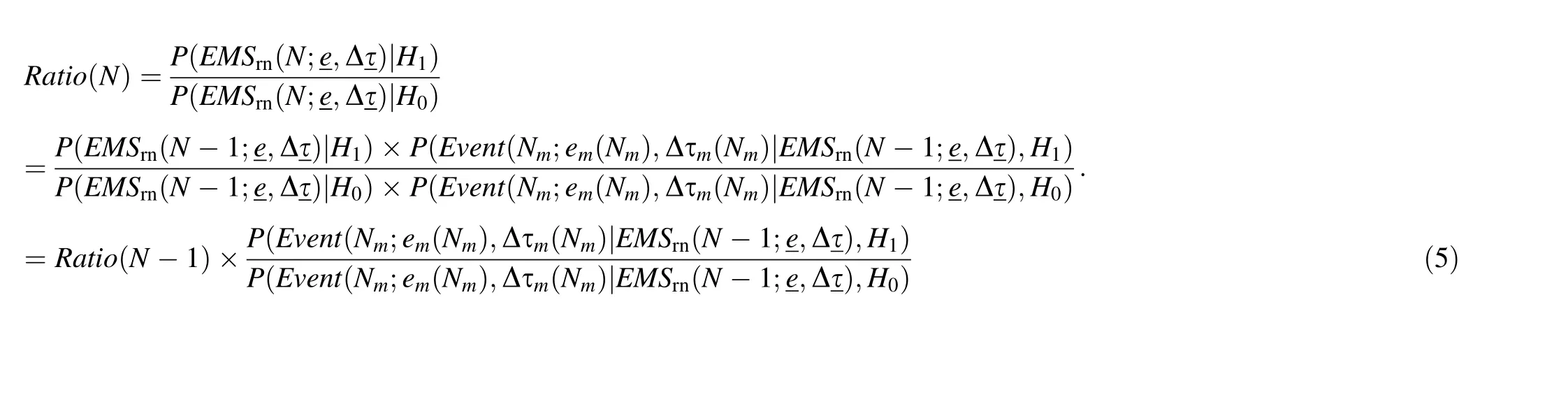
When a radionuclide identification instrument is placed in a public area,the background radiation is constant.For an EMS measured in the presence of natural background radiation,the region of interest(ROI)in the spectrum consists of the Compton platform and other types of background radiation.Therefore,we modeled the measured energy of a gamma ray emitted by a monoenergetic source in an ROI uniformly and the interarrival times exponentially.

The decision function Λ（N） is obtained by taking the logarithm ofRatio （N）,as shown in Eq.(6).

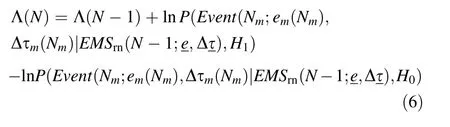
With theNth photon recorded by the detector,the posterior probabilistic distribution parameter of the EMS model underH1is estimated using Bayesian inference.The decision function is then updated according to the resulting parameters and compared to preset detection thresholds to obtain detection results.The Wald sequential probability ratio test result is defined in Eq.(7),whereT1andT0are the detection thresholds[29].

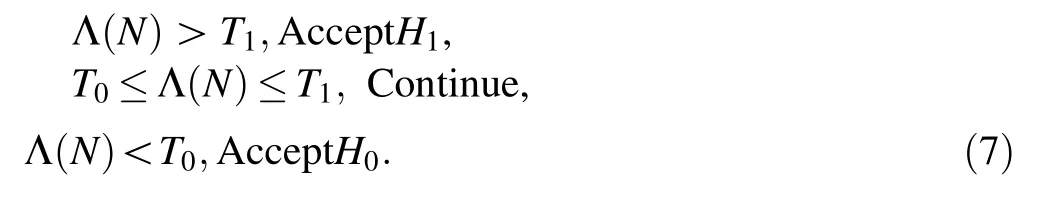
After defining a detection method,it is necessary to infer parameters and finalize a decision function.Based on the specified probability distribution form and observed data,the posterior distribution of themth monoenergetic source underH1is defined in Eq.(8),where the probabilistic model is decomposed by applying Bayes’rule[30,31]and αm（Nm） is the emission rate estimated by theNmth photon detected from themth monoenergetic source.

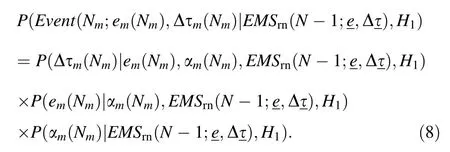
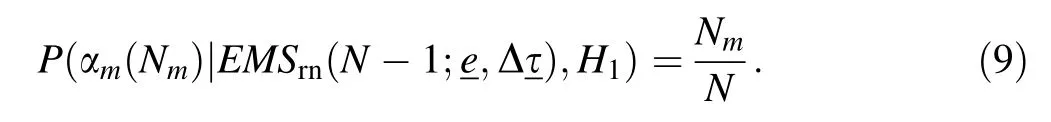
The measured energy of a photon detected from themth monoenergetic source is assumed to follow a Gaussian distribution underH1,as shown in Eq.(10).and σem（Nm） are the expected value and standard deviation of the posterior distribution,respectively.

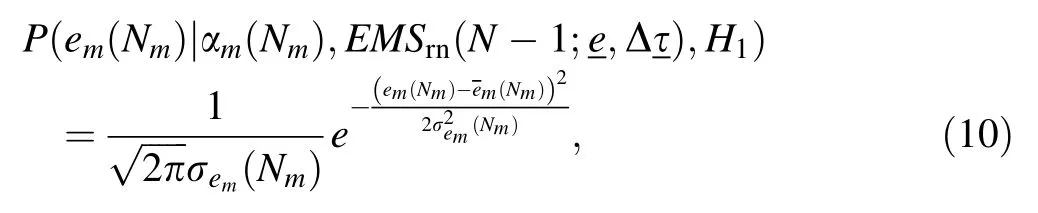
The arrival time interval Δτis exponentially distributed and λm（Nm） is the expected value.Therefore,the following equation can be derived:

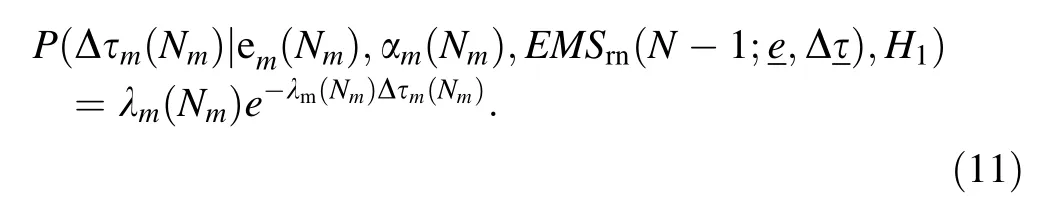
where

Then,the probabilistic model of the EMS under hypothesisH1is given by Eq.(12).

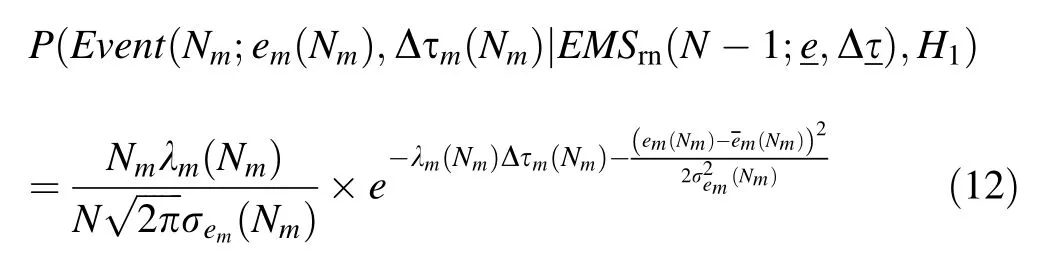
The probabilistic model of the EMS under hypothesisH0is given by Eq.(13).

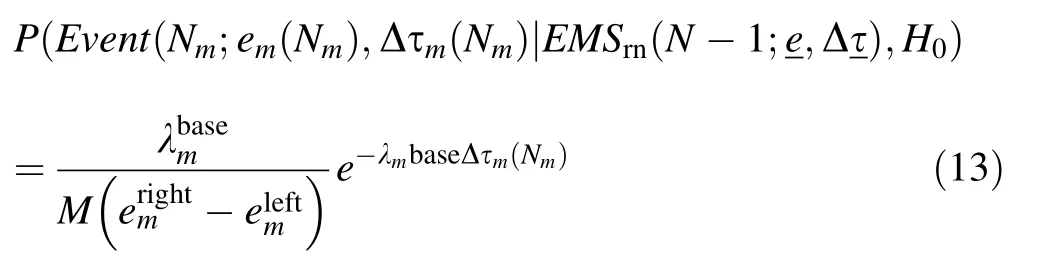
The decision function is obtained by substituting Eqs.(12)and(13)into Eq.(6),as shown in Eq.(14).

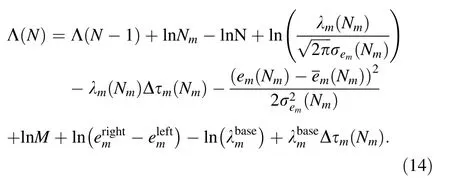
2.2 Implementation of the proposed method

First,a radionuclide identification instrument is installed in a public area to detect the EMS of the target radionuclide under conditions with natural background radiation for a long period(at least hundreds of seconds).The count rateof themth monoenergetic source in the natural background radiation is then obtained by taking average counts from the ROI.

Next,a parallel detection architecture is proposed to implement the sequential detection scheme.As shown in Fig.1a,there are two types of detection channels that process the detected photons emitted by a monoenergetic source.The first type is designed to infer the parameters of the probabilistic model and evaluate the log-likelihood under hypothesisH1,whereas the other evaluates the loglikelihood under hypothesisH0.When a photon is detected in the first type of channel,photon discrimination is performed.If an event is accepted by one of the channels,then posterior distribution parameter estimation is performed.Finally,the log-likelihood is calculated based on the probabilistic model under hypothesisH1with updated parameters.Event discrimination is first performed using the second type of channel.Finally,the proposed method performs a log-likelihood evaluation based on the probabilistic model under hypothesisH0with constant parameters.After an event is processed using the detection channels,the current decision function value is updated according to Eq.(14)and compared to the preset detection thresholds to obtain detection results according to Eq.(7).

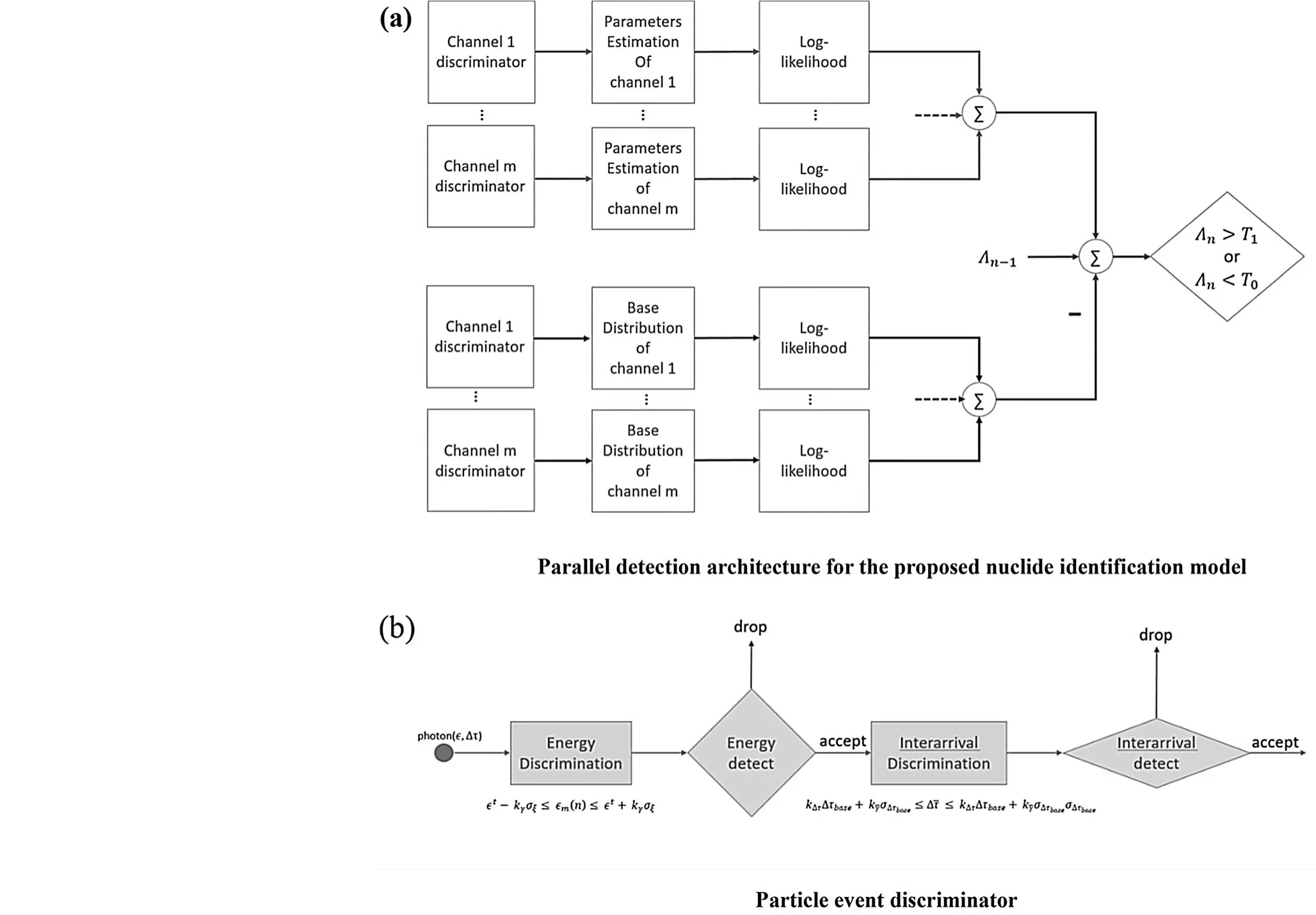
Fig.1 Detection architecture

A two-stage structure was designed to perform photon discrimination,as shown in Fig.1b.The energy discriminator is used to determine which channel a photon should be processed in,after which a detection rate discriminator uses the interarrival time for verification[13].The energy discriminator performs a confidence interval test,as shown in Eq.(15),wherenis the particle ordinal number,is the confidence coefficient of the energy,andandare the mean and standard deviation of the energy,respectively,which can be obtained experimentally.

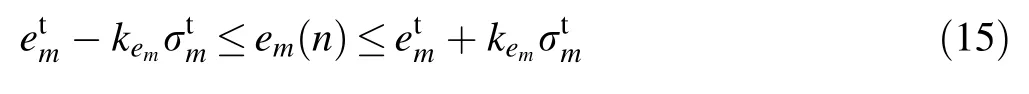
The interarrival time discriminator also performs a confidence interval test,as shown in Eq.(16).

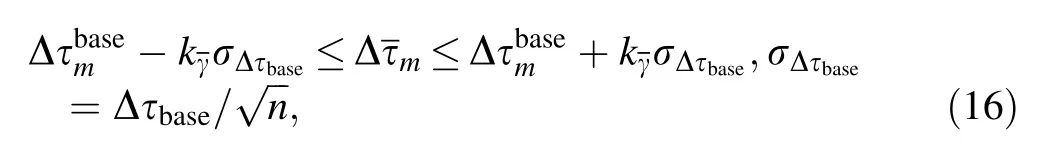
The posterior probability distribution parameter estimation of the EMS under hypothesisH1is achieved using Bayesian inference.Because energy is modeled as a Gaussian distribution and the interarrival time is modeled as an exponential distribution(both belonging to the exponential family of distributions),it is convenient to find conjugate prior distributions and infer the posterior distribution in analytical form.Following research on Bayesian inferencing[32,25],the Gaussian–Gamma distribution was applied to model the prior distribution ofandbecause the precision parameterprecemis defined as.The prior distributions（0）andare defined in Eq.(17),wherea0,b0,u0,andv0are hyperparameters[26].For a weak prior,u0is set to,a0andb0are set to one and 100,respectively,andλ0is set to one.

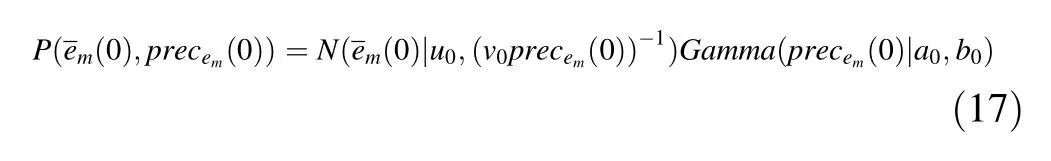
Equation(18)models the prior distributionλm（0）of the expected value of the interarrivalλmas Gamma.c0andd0are also hyperparameters,wherec0is set to one andd0is set to.

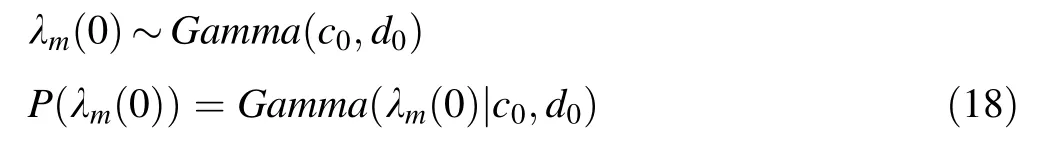
Up to thenth arrival from themth monoenergetic source,the posterior distributions of,τem（n）,and λm（n） are updated as shown in Eq.(19),whereun,vn,an,bn,cn,anddnare the hyperparameters of the posterior distributions[33].

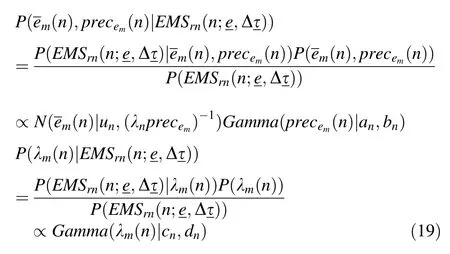
The hyperparameters can be inferred in analytical form[33]via conjugacy,as shown in Eq.(20).

The expectation of the posterior distribution can be used to obtain the parameters of the EMS model underH1.=un

Then,the decision function is updated according to the parameters and the detection result is obtained by comparing the decision function to the preset detection thresholds.If the decision function value exceeds the thresholdT1,a target radionuclide exists in the detection environment.If the decision function value exceeds the thresholdT0,then there is no target radionuclide in the detection environment.Otherwise,the detection process continues until one of the thresholds is exceeded.

3 Experiments

3.1 Background experiment

In this experiment,the spectrum of the background was recorded for a long duration.The count rate of the ROI was stable and the relative statistical error was small.The target radioactive sources were added and the spectrum was collected to form a stable spectrum.The energy distribution model of the characteristic peaks in the ROI was then analyzed.

For a target radionuclide,the count rate of the ROI in the background can be obtained through a long-term detection experiment[34].137Cs and60Co were selected as target radionuclides.The radioactivity of the137Cs source was 131000 Bq and the radioactivity of the60Co source was 7000 Bq.A LaBr3(Ce)detector of sizeφ3?81 cm×3?81 cm was used in this experiment.The EX-03 multichannel analyzer was developed by the Chengdu University of Technology to obtain the EMS.The parameters for Eqs.(15)and(16)are listed in Table 1.The experiment was performed in a laboratory environment to obtain the count rate of the ROI in the background and the detection time was set to 276 s.The threshold used in this study was obtained experimentally and the results of the experiments demonstrated that a threshold of 3.98 is acceptable.

Table 1 Preset detection parameters

The spectrum and EMS detected in the background are presented in Fig.2.The ROIs in the spectrum are labeled with red,blue,and green regions.The ROI of137Cs ranges from 651 to 671 keV.The first ROI of60Co ranges from 1154 to 1186 keV and the second ROI of60Co ranges from 1310 to 1350 keV.It is clear that the counts in the ROI approximately follow a uniform distribution.

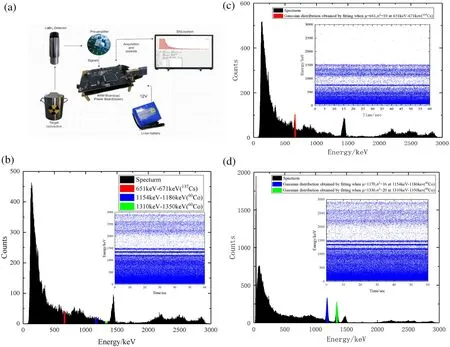
Fig.2 (Color online)Detected EMS and spectra in different radiation fields.a Description of the test bench;b Spectrum obtained under background conditions with a detection interval of 250 s;c 137Cs radiation energy spectrum;d 60Co radiation energy spectrum

Figure 2a presents a description of the test bench.Figure 2b presents the energy spectrum and EMS time-domain scatter diagram for natural background radiation.Figure 2c presents the energy spectrum and EMS time-domain scatter diagram of the target nuclide137Cs and natural background radiation.Figure 2d presents the energy spectrum and EMS time-domain scatter diagram of the target nuclide60Co and natural background radiation.

Mathematically,the Chi-square goodness-of-fit test was performed to validate that the energy detected in the ROI under natural background radiation conforms to a uniform distribution[33].The relevant formula is presented in Eq.(22),where LeftChannel and RightChannel are the edges of the selected ROI,Spectrumiis the count of theith channel in the spectrum,andTis obtained by taking the average of the counts in the ROI.

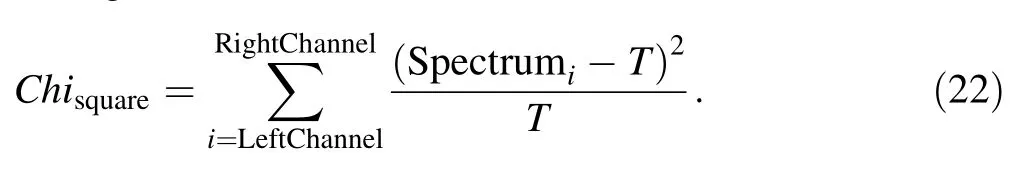
For the ROI of137Cs,the Chi-square test result was 34.37.For the first ROI of60Co([1140,1180]keV),the result was 20.62 and for the second ROI of60Co([1300,1360]keV),the result was 35.80.The calculated Chisquare values were compared to the 95%confidence threshold values,which were 55.76,79.08,and 79.08,respectively.All of the calculated values are less than the corresponding threshold values,indicating that the energy in the ROI measured under the background conditions was uniformly distributed.

The count rate of the ROI under natural radiation background,denoted asλΔτbase,was also calculated.The average interarrival timeΔτbasewas obtained by taking the reciprocal of the count rate.The average count rates in the background for[651,671]keV,[1154,1186]keV,and[1310,1350]keV were 2.35,5.14,and 0.57 per second,respectively.

The rapid nuclide identification method was used to detect target radionuclides under background conditions.The detection results for137Cs under background conditions are presented in Fig.3a.The detection function gradually decreases along with events that are processed until the detection function exceeds the low threshold,indicating that the background is detected in 5 s.The detection results for60Co under background conditions are presented in Fig.3b.This detection function also gradually decreases with the events that are processed until the detection function exceeds the low threshold,indicating that60Co is absent in the background.

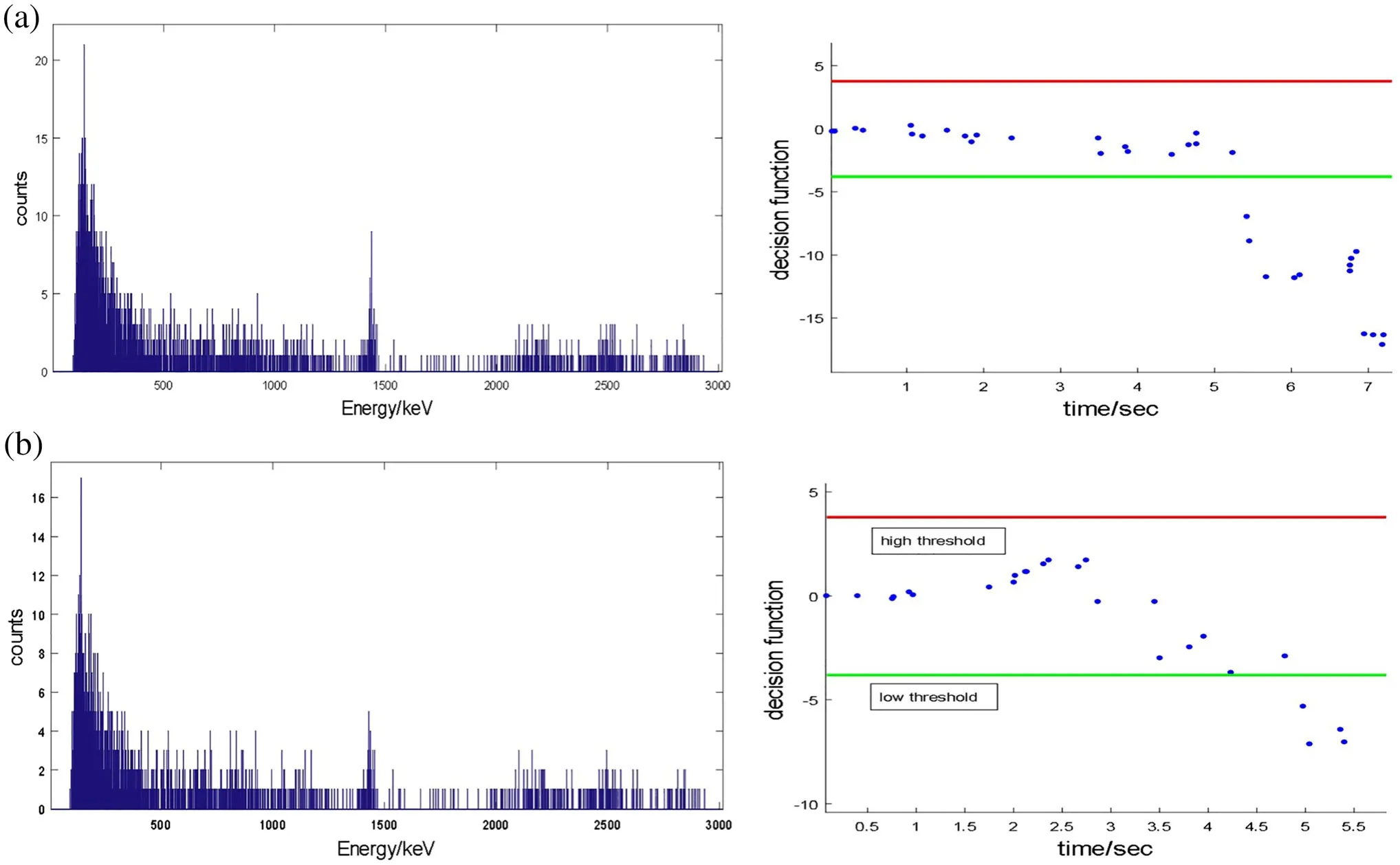
Fig.3 137Cs and 60Co Detection results under background radiation conditions

3.2 Radionuclide detection experiment

The137Cs source was placed 150 cm in front of the LaBr3detector to verify the proposed method under a radiation field and detection was performed for 100 s.The detected EMS and spectrum are presented in Fig.2b.A fitted Gaussian function(red line)is placed above the ROI,and it is clear that the energy detected in the ROI under a radiation field approximately follows a Gaussian distribution.In addition to this graphical depiction,the Chi-square test was performed to validate that the energy detected in the ROI under a radiation field approximately follows a Gaussian distribution.The relevant formula is presented in Eq.(23).

where Left Channel and RightChannel are the edges of the selected ROI,Spectrumiis the count of theith channel in the spectrum,and IntegralValue is obtained using Eq.(24).

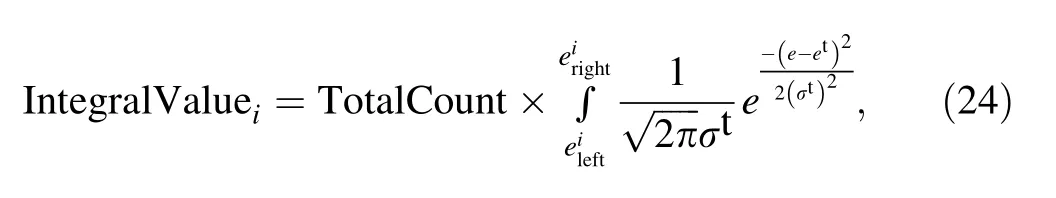
where TotalCount is the total count in the ROI,andeileftandeirightare the left and right energies of theith bin in the spectrum,respectively.Additionally,etandσtare preset distribution parameters by the posterior probability distribution parameter estimation(Table 1).

The Chi-square test result for the ROI[641,681]was 50.20.When comparing the Chi-square value to the value of the 95%confidence threshold of 55.76,the calculated value is less than the threshold,indicating that the energy spectrum in the ROI under the137Cs radiation field and long-term detection conforms to a Guassian distribution.

A rapid nuclide identification method was used to detect137Cs in the corresponding radiation field.The detection distance is 35 cm.The detection function is presented in Fig.4a,where the decision function gradually increases with events that are processed and eventually exceeds the high threshold,indicating that the137Cs source is detected in 4.1 s.

There were only a few counts in the ROI before137Cs that were identified and the counts in the ROI were not sufficient to form a peak.According to Eqs.(23)and(24),the Chi-square test was performed to determine whether the spectrum in the ROI follows a Gaussian distribution.The test value was 41.76,which is greater than the threshold value of 31.41,indicating that traditional fullspectrum-analysis-based radionuclide identification methods cannot identify137Cs at low values.

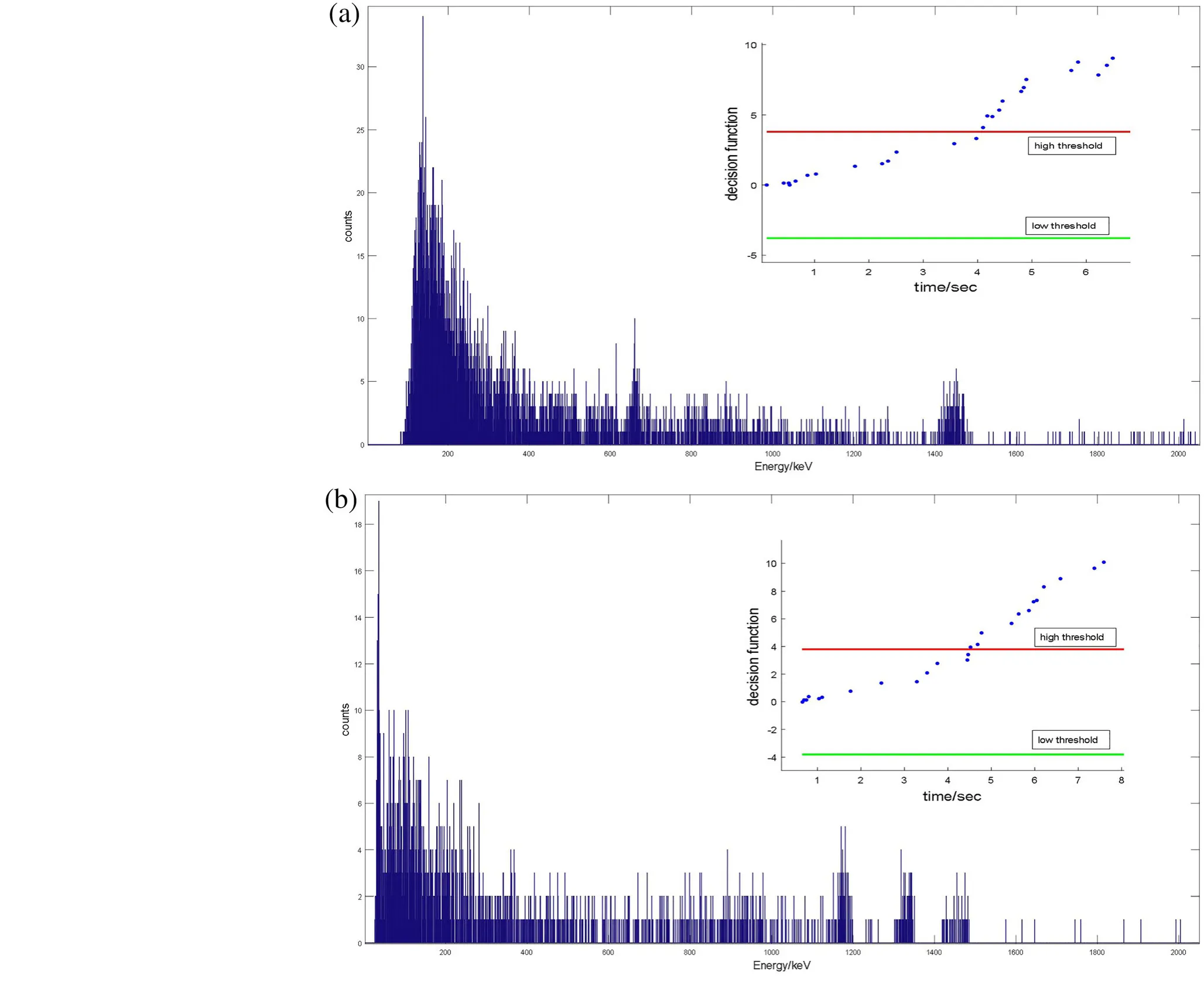
Fig.4(Color online)137Cs and 60Co decision results in 137Cs and 60Co spectra.a Decision function and spectrum obtained when 137Cs is identified.b Decision function and spectrum obtained when 60Co is identified

The60Co source was placed 10 cm in front of the LaBr3detector and detection was performed for 100 s.The EMS and spectrum detected are presented in Fig.2c,where two fitted Gaussian functions(red and blue lines)are placed in the ROI.The energy detected in the ROI under the60Co radiation field approximately follows a Gaussian distribution.By using Eqs.(23)and(24),the Chi-square test was also performed for validation.

The Chi-square test results for ROI[1140,1180]and[1300,1360]keV were 66.67 and 74.21,respectively.The calculated Chi-square values were compared to the values of the 95%confidence threshold,which were 79.08 and 79.08,respectively.All calculated values were less than the threshold values,indicating that the energy in the ROI detected in the spectrum under radiation and long-term detection conforms to a Gaussian distribution.

The rapid nuclide identification method was used to detect60Co in the corresponding radiation field.When the detection distance is 10 cm,the detection results are presented in Fig.4b,the decision function gradually increased with events that are processed and eventually exceeds the high threshold,indicating that there is a60Co source in the radiation field,indicating that the60Co source is detected in 4.6 s.Only a few counts in the ROI before60Co were detected.To determine if the counts in the ROI were insufficient to form a peak,according to Eqs.(23)and(24),a Chi-square test was performed to demonstrate that the spectrum in the ROI did not follow a Gaussian distribution.The test values of the ROIs of[1155,1185]keV and[1310,1350]keV were 48.59 and 60.34,respectively,and the 95%confidence threshold values were 43.77 and 55.76,respectively.It is clear that the calculated values are greater than the detection thresholds.Therefore,traditional fullspectrum-analysis-based radionuclide identification methods cannot identify60Co with such a low counts.

3.3 Detection performance experiments

Experiments were conducted while varying the distance between the source and detector to evaluate the performance of the proposed method.The step length was 5 cm and the distance ranged from 5 to 100 cm.For each distance,the detection experiments were repeated 20 times to analyze the statistics of the identification time.The average detection time and variance for each test group were calculated and plotted.The results for the identification time required to cover the distance between the source and detector are presented in Fig.5.

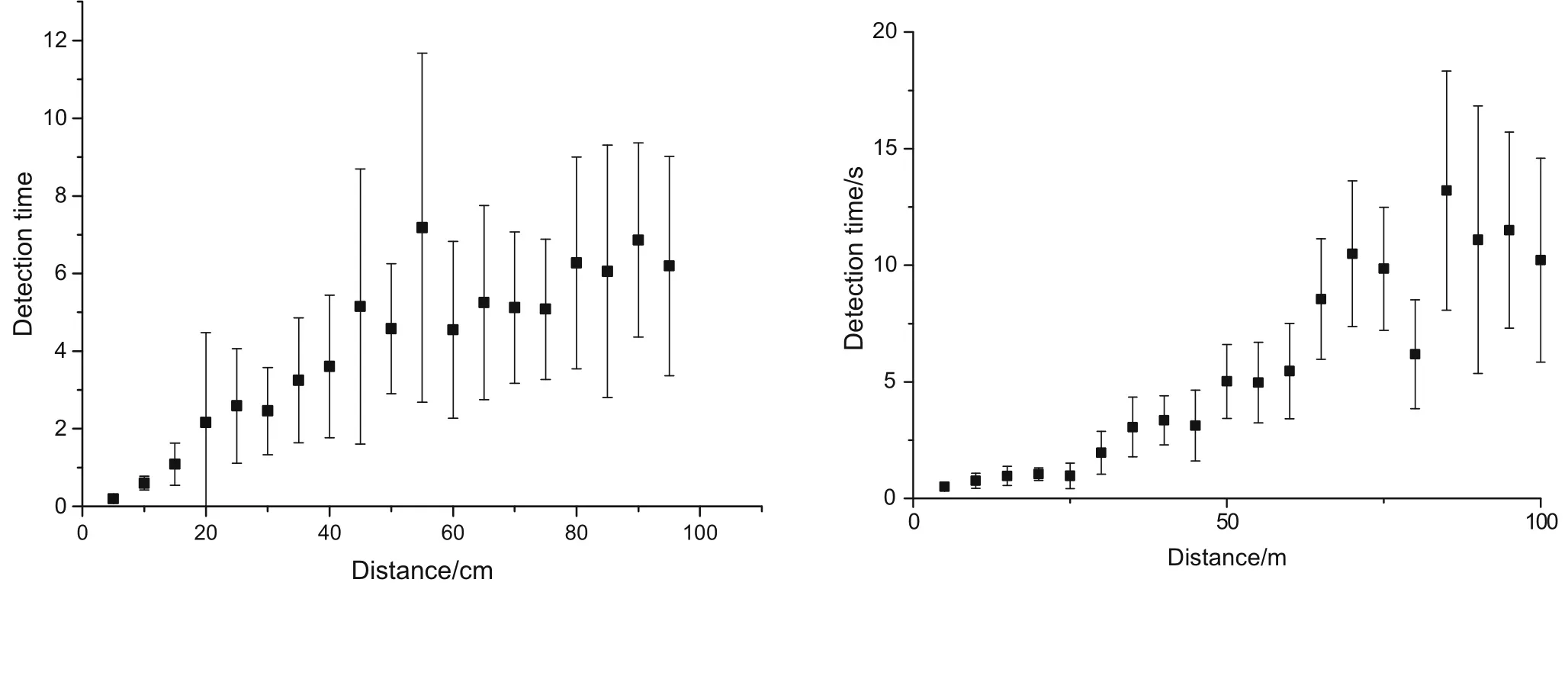
Fig.5 Relationship between detection time and detection distance.Identification times required to cover the distances to the 137Cs source with an activity of 131000 Bq(left)and 60Co source with an activity of 80400 Bq(right)

As shown in the figure above,when the detection distance is set to 5 cm,the137Cs detection time is 0.2 s.As the distance increases,the detection time also increases.When the distance reaches 90 cm,the average detection time increases to 7 s.For the measurement of60Co,the average detection time is within 2 s when the detection distance is within 25 cm.As the detection distance increases,the detection time also increases and the relative distance reaches 60 cm.The average detection time is 6 s,which meets the requirements for rapid identification.

4 Conclusions and prospects

Based on the Bayesian sequential detection method,this paper introduced a rapid nuclide identification method for radionuclide inspection in public areas.Unlike other traditional full-spectrum-analysis-based methods,in this study,based on the EMS measurement of background radiation and the target radiation field,two EMS sequences were established,a priori models were estimated based on effective particle events,and an a posteriori model was obtained.The target nuclides were identified via sequential detection of the posteriori models.

To prove that the efficiency of the proposed background-comparison-based radionuclide identification method can meet the requirements of rapid identification under different measurement conditions,several groups of experiments were conducted.The relative distance between the detector and two radioactive sources was controlled and multiple measurements were performed at distances of 0 to 100 cm to obtain detection time curves for the radioactive sources.The average detection time was 6.0 s for60Co(with an activity of 80400 Bq)at a distance of 60 cm from the detector.The average detection time was 7 s for137Cs(with an activity of 131000 Bq)at a distance of 90 cm from the detector.These results demonstrate that rapid nuclide identification can be achieved using the proposed background-comparison-based radionuclide identification method.

To improve the adaptability of the proposed method to complex environments,further research should focus on the rapid detection and identification of radionuclides in multiple-nuclide mixtures under conditions with complex motion.

Author contributionsAll authors contributed to the study conception and design.Material preparation,data collection and analysis were performed by Xiao-Zhe Li,Qing-Xian Zhang,He-Yi Tan,Zhi-Qiang Cheng.The first draft of the manuscript was written by Xiao-Zhe Li and all authors commented on previous versions of the manuscript.All authors read and approved the final manuscript.