Magnetic phase diagram of single-layer CrBr3?
Wei Jiang(江偉) Yue-Fei Hou(侯躍飛) Shujing Li(李淑靜) Zhen-Guo Fu(付振國) and Ping Zhang(張平)
1Institute of Applied Physics and Computational Mathematics,Beijing 100088,China
2Beijing University of Chemical Technology,Beijing 100029,China
3School of Physics and Physical Engineering,Qufu Normal University,Qufu 273165,China
Keywords: magnetic anisotropy,single-layer CrBr3,N′eel-antiferromagnetic phase
1. Introduction
Since the discovery of graphene,[1,2]the two-dimensional(2D)materials have attracted a lot of interests during the past two decades. 2D materials become very important in modern condensed matter physics and introduce many novel ideas to our communities. The electronic and optical properties have been studied explosively in graphene, silicene, and transition metal dichalcogenides,[3–5]etc., but the 2D magnet is still a part to be further studied. The reason may be, differing from the bulk materials, that the long-range magnetic order in 2D materials is prohibited[6–8]by Mermin–Wagner theorem at finite temperature.[9]However, more and more studies reveal that magnetic anisotropy, which originates mainly from spinorbit coupling,[10]can overcome this restriction and thus becomes an important parameter for 2D magnets.
In recent years,many intrinsic ferromagnetisms in atomically thin magnets have been widely studied in various van der Waals materials, including rare-earth chalcohalides REChX(RE=rare earth; Ch=O, S, Se, Te;X=F, Cl, Br, I),[11]metallic Fe3GeTe2,[12–14]semiconducting Cr2Ge2Te6[15,16]and insulating CrI3.[17–19,23–29]Among them, single-layer CrBr3(SL-CrBr3) gradually attracted the attention of scientists. For example, recently, Zhanget al.have experimentally demonstrated the intrinsic ferromagnetism in SLCrBr3and reported the spontaneous magnetization persistence with a Curie temperature of 34 K.[30]The magnon-assisted tunneling and the magnetic proximity effects in van der Waals heterostructures based on CrBr3have also been widely studied.[31–34]For example, the charge-state dependency of the magnetic proximity effects in MoSe2/CrBr3van der Waals heterostructures has been studied via low-temperature magneto-optical spectroscopy experiments,which conformed with that the valley polarization of the MoSe2trion state may be remarkably related to the local CrBr3magnetization,while the neutral exciton state remains insensitive to the ferromagnet.[32]These discoveries provide us sufficient opportunities for both fundamental studies and spintronics applications.
Compared with the vigorous development of experimental research,the theoretical research on the magnetism of SLCrX3is somewhat lacking. In-depth understanding and control of the magnetic properties of SL-CrX3will help the development of low-dimensional spintronic devices based on SLCrX3. Strain engineering and charge doping are two widely used methods to introduce new phases and effectively tune magnetic properties of the 2D structures.[19–22,35–39]For instances,on one hand,in strain engineering,Lucaset al.have reported the strain-tunable magnetic anisotropy energy(MAE)in 2D SL-CrX3(withX=Cl, Br, and I),[36]and on the other hand,charge doping is applied to tune the magnetic properties of SL-CrI3.[19]
To our knowledge,up to now,the influences of strain and charge doping on the magnetic properties of SL-CrBr3have not been discussed in detail in the present literatures. However, a detailed understanding on fundamental properties of SL-CrBr3plays an important role in realizing its potential applications in spin-base technologies. Owing to the interest and importance from the perspectives of both basis physics and potential applications of SL-CrBr3in the fields of spintronics, it is timely to provide a theoretical analysis of the magnetic phases of SL-CrBr3tuned by strain effect and charge doping. Therefore, in this work, by employing systematical first-principals calculations and Heisenberg model simulations, we theoretically investigate the magnetic phase transitions in SL-CrBr3induced by reasonable strains and charge doping. Three different magnetic ground states,including offplane ferromagnetic (FM), in-plane FM and in-plane N′eelantiferromagnetic(N′eel-AFM)phases,are found in our calculations. Furthermore,a Heisenberg Hamiltionan,which takes into account the third-nearest-neighbor Heisenberg exchange parameter and next-nearest-neighbor anisotropy exchange parameter,is used to accurately explain the magnetic phase transition in SL-CrBr3. The Curie temperature we obtained is aboutTC=38.4 K, which is in good agreement with the experimental result 34 K.[30]
2. Calculation details
Our density functional theory (DFT)[40,41]calculations are performed by using the Viennaab initiosimulation package.[42]The exchange–correlation functional is subjected to the generalized gradient approximation (GGA) in Perdew, Burke, and Ernzerhof (PBE) form.[43]Core electrons are treated with the projected augmented wave (PAW)method[44–46]and the valence electrons are calculated on a plane wave basis with a cut-off energy of 350 eV. The vacuum space is chosen as 15 ?A,which is large enough to avoid the layered interactions. A 9×9×1 Monkhorstk-point mesh is set for Brillouin zone integrations. All structures are optimized until the total energy is converged to be with 10?8eV and the Hellmann–Feynman force on each atom is smaller than 0.001 eV/?A. To characterize the stability of SL-CrBr3,we also calculate the elastic constant by employing AELAS code.[47]To extract both Heisenberg exchange parameters and anisotropy exchange parameters, a three-neighborXXZHeisenberg model Hamiltonian[19]is employed to fit the total energies in our DFT calculations for different spin configurations on a honeycomb lattice. In addition, the Curie temperature is estimated by using SpinW[48]simulations in which a 100×100×1 honeycomb lattice is used. The SpinW simulations involve 104Monte–Carlo(MC)steps per site in order to accurately obtain thermal equilibrium for each temperature.In the following text, the level of doped carriers per Cr atom is expressed asδn=n?n0(in units ofe/Cr), where the intrinsic valence electron number of each Cr atom,and positive and negative values represent electron doped (e-doped) and hole doped (h-doped) states, respectively. For strained SL-CrBr3,the quantity of strain is defined asε=(a?a0)/a0, whereaanda0are the horizontal lattice constants of the strained and the intrinsic SL-CrBr3,respectively.
3. Results and discussion
The optimized atomic structure of SL-CrBr3is shown in Figs.1(a)and 1(b).For the intrinsic structure,Cr atoms share a honeycomb lattice with a lattice constanta0=6.44 ?A.Six Br atoms constitute a slightly distorted octahedron around each Cr atom. Here,we consider four spin configurations to realize the FM, N′eel-AFM, stripy-antiferromagnetic (stripy-AFM),zigzag-antiferromagnetic (zigzag-AFM) orders, as plotted in Figs. 1(c)–1(f). Both off-plane and in-plane orientations of magnetic moment of Cr are calculated to analyze the magnetic phase and MAE.In order to systematically study the magnetic states of SL-CrBr3, the calculations on strain and charge effects are performed. In the following calculations, the strain strengthεchanges from?10%to 15%,and the doped carriersδnchanges from?0.25 to 0.25.
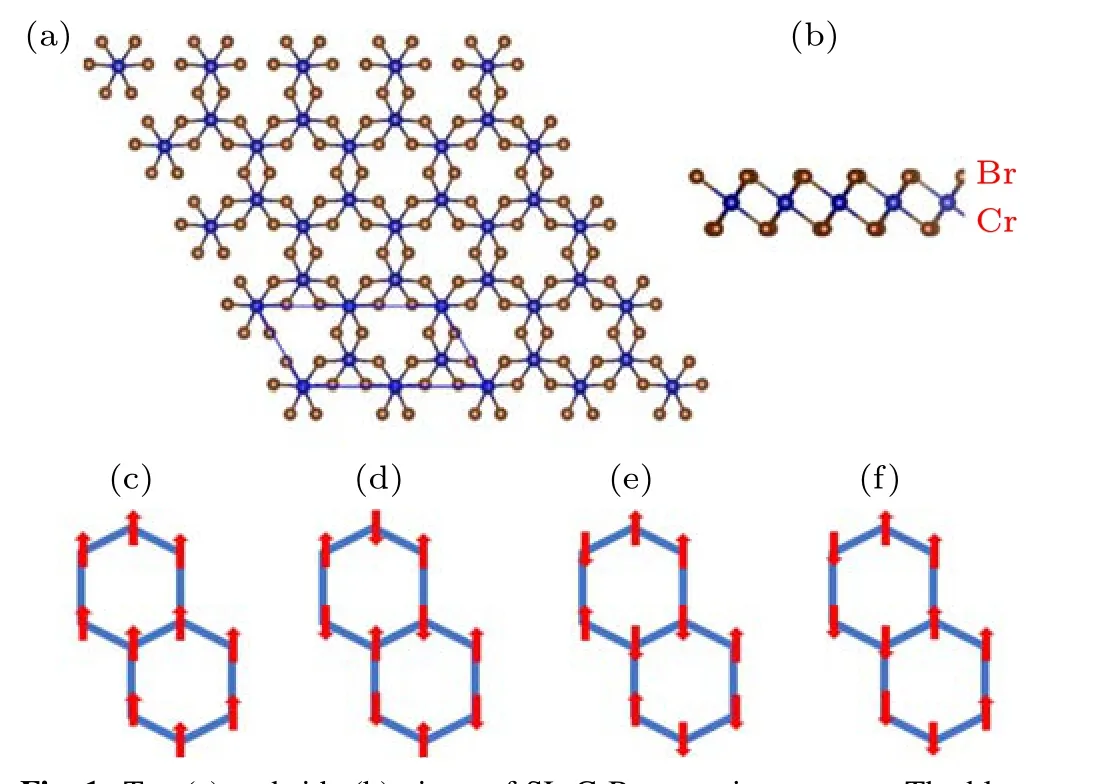
Fig.1. Top(a)and side(b)views of SL-CrBr3 atomic structure. The blue parallelogram in (a) shows the unit cell. FM, Neel-AFM, stripy-AFM and zigzag-AFM orders are shown in(c)–(f),respectively,where the red arrows represent the spin orientations.
Before discussing the magnetic orders of SL-CrBr3,which are tuned by strain and charge doping,it is necessary to clarify whether the structure of SL-CrBr3is stable under external strain. Our DFT calculations show that the 2D Young’s modulus of SL-CrBr3is 27 N/m, which is nearly an order smaller than that of graphene (340 N/m)[49]and SL-MoS2(180 N/m).[50]This means that SL-CrBr3is much softer comparing with other typical 2D magnets. Therefore,it is possible for us to explore the magnetic phase diagram of SL-CrBr3in a large range of strain and charge doping. In addition, the stability of SL-CrBr3under strain and charge modulations are also carefully checked by phonon dispersion calculations by using the phonopy code.[51]The phonon results, which are not shown for briefness, show that the structure of SL-CrBr3is stable in the strain and doping regimes we considered in this work. The stability of SL-CrBr3may make it a promising candidate for the potential application in the low-dimensional spintronics.


Fig.2.Total energy differences ?E(in meV/Cr)of SL-CrBr3 in zigzag-AFM(black squares),stripy-AFM(red dots),and N′eel-AFM(blue triangles)orders relative to the off-plane FM order as functions of strain strength ε.
Since the origin of long-range intrinsic ferromagnetism originates from magnetic anisotropy,[30]the modulation of strain effect on the MAE is also quantitatively analyzed in this work. The corresponding results are represented in Fig.3. We can see that the magnetic anisotropies for each magnetic order are similar to each other. For SL-CrBr3with normal lattice constant,the magnitude of MAE is about~220μeV/Cr,which is smaller than that in SL-CrI3(800μeV/Cr).[19]This is possibly due to the stronger spin–orbital coupling (SOC) effect in I atom than that in Br atom. When SL-CrBr3is biaxially compressed (i.e.,ε< 0), MAE turns smaller. In the N′eel-AFM phase,MAE of SL-CrBr3is negative,which means that the spin orientation is in-plane, and thus the stable magnetic phase is in-plane N′eel-AFM.If the stretching strain is applied,the MAE slowly increases at first and then gradually decreases with the increase of the strain intensity. Whenε=9%, the MAE reaches the maximum value. Here,MAE is always positive, which indicates that the spin orientation for FM order is off-plane. Therefore, the stable magnetic phase should be off-plane FM when SL-CrBr3is stretched.
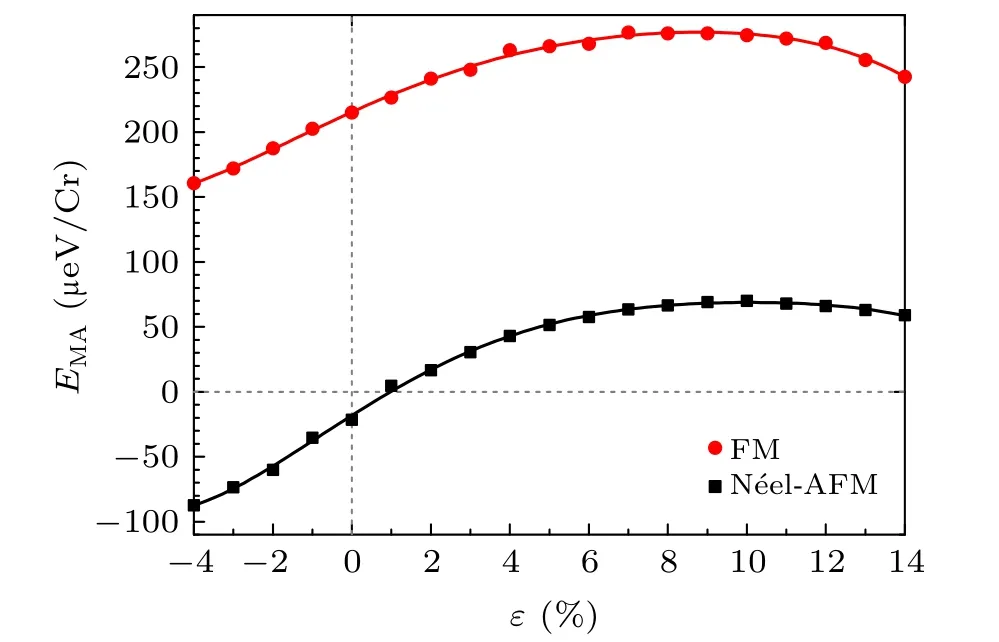
Fig.3. Magnetic anisotropy energies EAM (in units ofμeV/Cr)for FM(red dots),and N′eel-AFM(black squares)of SL-CrBr3 as functions of strain strength ε.
To explore the physical mechanism of magnetic properties of SL-CrBr3under strain (ε/= 0) without charge doping (δn= 0), a three-neighborXXZHeisenberg model Hamiltonian[19]is employed. Explicitly, the effective magnetic energy terms in different magnetic phases considered in this work are expressed as
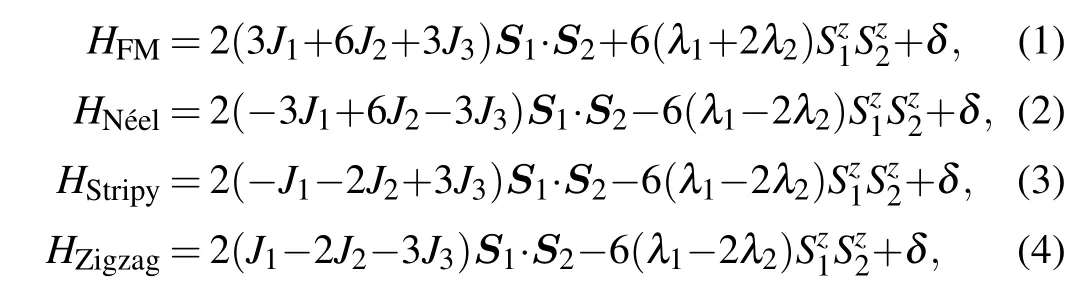
where the first-, second-, and third-nearest-neighbor Heisenberg exchange parametersJn(n=1,2,3), as well as the first and second anisotropy exchange parametersλn(n=1,2) are considered,Si=1,2denote the spin of Cr. Here,J2andJ3are needed to accurately analyze the magnetic phase and estimate the curie temperature in turn.λ1is good enough to explain the magnetic anisotropy at zero strain but it is necessary to takeλ2into consideration under large compressive or tensile strain.In our calculations, the magnetic moment of Cr atoms is about 3.0μB. Compared with the non-doped and unstrained cases,DFT calculations show that the magnetic moment of Cr atoms varies less than±5%with the strain intensity and doping concentration. Therefore, in the fitting of the Heisenberg model parameters,the dependence of the magnetic moment on strain and charge doping is ignored.
The fitted Heisenberg exchange parameters are shown in Fig. 4(a). It is obvious thatJ1has the largest magnitude and dominates the magnetic states in SL-CrBr3. In briefness,J1is negative when system is in FM phase while positive when system is in AFM phase. This can be easily understood sinceJ1represents the exchange interaction between the nearestneighbor Cr atoms. With increasing the strain from?8% to 15%,the second-nearest and third-nearest neighboring effects become weaker so thatJ2andJ3become smaller in magnitude,which could be obviously seen from Fig. 4(a). Since CrBr3honeycomb lattice presents two sub-lattices,J2acts within each sub-lattice andJ3acts between the two sub-lattices. In SL-CrBr3,J2is always negative andJ3is always positive. The negative sign ofJ2indicates that the atoms within one sublattices favor to align ferromagnetically,while the positive sign ofJ3indicates that two sub-lattice favor to align antiferromagnetically.

Fig. 4. (a) Fitted Heisenberg exchange parameters Jn (n=1,2,3), and(b) anisotropy exchange parameters λn (n=1,2) as functions of strain strength ε in SL-CrBr3 without charge doping (δn = 0). The curves of λ1?2λ2 (blue curve)and λ1+2λ2 (green curve)are also plotted in(b).
The fitted anisotropy exchange parameters are shown in Fig.4(b).λ1is always negative and has larger magnitude.λ2is negative whenε>?6%and becomes positive when SL-CrBr3is heavily compressed. We know from Fig. 1(a) that each Cr atom has three nearest Cr atoms and six second-neighbor Cr atoms, and thus the MAE should be proportional toλ1+2λ2(λ1?2λ2) for FM (AFM) order. It is clearly shown by the green cure in Fig. 4(b) that whenε>?4.2%,λ1+2λ2is always negative,and thereby the orientation for FM order is always off-plane in our strain range. Similarly,λ1?2λ2is negative whenε
Based on our calculations,Jn(n=1,2,3)are much larger thanλn(n=1,2), andJ1is the largest in magnitude. As depicted in Fig.2,the relative stable AFM phase at the intrinsic structure is zigzag-AFM. We adopt the Hamiltonian of FM and zigzag-AFM order to estimate Curie temperature for the intrinsic SL-CrBr3with a lattice constanta0. The result of our SpinW simulations isTC=38.4 K,which is well consistent with the experimental result 34 K.[30]We also perform calculations only considering the nearest neighbor Heisenberg exchange parameterJ1and first anisotropy exchange parameterλ1. The corresponding Curie temperature is estimated asTC=40.1 K,which becomes worse comparing with the experimental result. Therefore, we believe that our three-neighborXXZHeisenberg model Hamiltonian is more accurate since it can contain more magnetic orders.
All above analysis are for the strain effect on the magnetic order transitions in SL-CrBr3. In the absence of charge doping,external strain induces a magnetic phase transition between off-plane FM order and in-plane N′eel-AFM order in SL-CrBr3,which is different from the case of SL-CrI3.[19]Following the same way,one could investigate the effect of charge doping with and/or without strain on the magnetic order transitions in SL-CrBr3. Here, for briefness, we will not discuss the case that only charge doping effect is taken into account.Therefore, we explore the magnetic phase diagram via strain engineering and charge doping. The result is shown in Fig.5.From Fig. 5, we can clearly see that in the strain and charge doping regimes we studied,there are three different magnetic phases in SL-CrBr3, which are off-plane FM (green region),in-plane FM (yellow region) and in-plane N′eel-AFM (cyan region). There are at least four points need to be noticed in Fig.5: (i)Consistent with the aboe discussions,for the intrinsic SL-CrBr3(ε=0 andδn=0), the magnetic ground state should be off-plane FM order. (ii)If there is no charge doping(δn=0)in the system but with certain strain(i.e.,εchanges from?10%to 15%),SL-CrBr3will undergo a magnetic phase transition from the in-plane N′eel-AFM to the off-plane FM.The corresponding phase transition point is aboutε=?4.2%,which is also in agreement with above analysis. (iii) Conversely,if strain is not applied on the system(ε=0)but there exists charge doping (δn/=0), Fig. 5 shows that as the doping concentration increases from negative value to positive value, the magnetic ground state will be modulated from the off-plane FM into the in-plane FM.The phase transition point is at the doping concentration ofδn=0.06e/Cr(see point A marked in Fig.5),(iv)The magnetic phase of the system could be simultaneously modulated by charge doping and external strain. Through detailed calculations, the phase boundaries among three different magnetic phases are obtained (see the black curves in Fig.5). The intersection of the three magnetic phases is approximately atε=?4.2% andδn=0.07e/Cr(see point B marked in Fig.5). In detail, the phase boundary between in-plane N′eel-AFM and in-plane FM is localized atε=?4.2%. In other words, whenδn>0.07e/Cr, the phase transition between in-plane N′eel-AFM and in-plane FM responds significantly to the strain effect. In this case,when the strain is slightly greater (less) than?4.2%, the system will come into in-plane FM (N′eel-AFM) order. When the charge doping is less than 0.07e/Cr, with the compressive biaxial strain increasing,the system tends to transform from off-plane FM to in-plane N′eel-AFM.
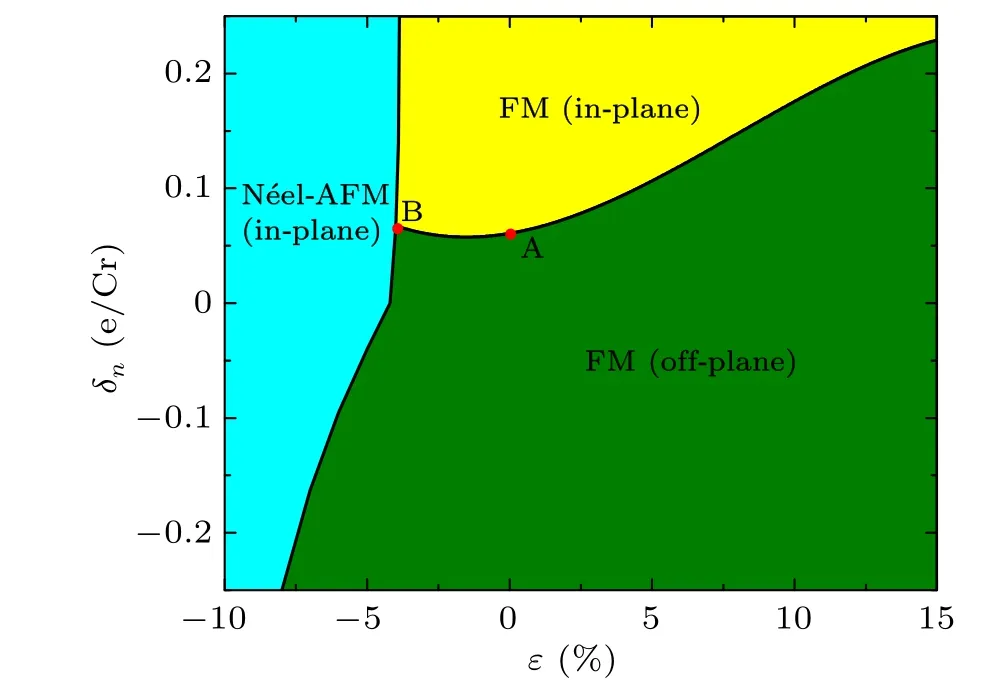
Fig.5. Magnetic phase diagram of SL-CrBr3 in the strain and charge doping regimes. Point A represents the phase transition at intrinsic structure with a normal lattice constant a0. Point B indicates the intersection of three magnetic phases.
4. Conclusion
In summary, we applied DFT calculations and model Hamiltonian simulations to investigate the magnetic properties of the recently discovered 2D ferromagnet, SL-CrBr3.The ground state is confirmed to be FM, which is consistent with the previous experiment. CrBr3exhibits strong magnetic anisotropy(215μeV/Cr)with an off-plane easy axis.We studied the effect of strain engineering and charge doping on SLCrBr3,and provided a magnetic phase diagram with rich tunable physics. The magnetic properties are remarkably dominated by strain,which have extensive impact on local spin and thus dominate the phase transition between the FM and AFM phases.Under particular strain,charge doping(especially hole doping)can also modulate the spin orientation and in turn manipulate magnetic states. Based on our fitted Heisenberg exchange parameters and anisotropy exchange parameters, we systematically analyzed the magnetic properties and estimated Curie temperature as 38.4 K.We also found that phase transition from the FM order to the N′eel-AFM order is dominated by the nearest-neighbor exchange parameterJ1, while the phase transition from the off-plane FM to the in-plane FM is influenced by MAE. The rich tunable magnetic properties make SL-CrBr3a reliable and promising candidate for potential application in spintronics.
- Chinese Physics B的其它文章
- Modeling the dynamics of firms’technological impact?
- Sensitivity to external optical feedback of circular-side hexagonal resonator microcavity laser?
- Controlling chaos and supressing chimeras in a fractional-order discrete phase-locked loop using impulse control?
- Proton loss of inner radiation belt during geomagnetic storm of 2018 based on CSES satellite observation?
- Embedding any desired number of coexisting attractors in memristive system?
- Thermal and mechanical properties and micro-mechanism of SiO2/epoxy nanodielectrics?

