Accurate GW0 band gaps and their phonon-induced renormalization in solids*
Tong Shen(申彤) Xiao-Wei Zhang(張小偉) Min-Ye Zhang(張旻燁)Hong Jiang(蔣鴻) and Xin-Zheng Li(李新征)
1Interdisciplinary Institute of Light-Element Quantum Materials,Research Center for Light-Element Advanced Materials,and Collaborative Innovation Center of Quantum Matter,Peking University,Beijing 100871,China
2State Key Laboratory for Artificial Microstructure and Mesoscopic Physics,Frontier Science Center for Nano-optoelectronics and School of Physics,Peking University,Beijing 100871,China
3International Center for Quantum Materials,Collaborative Innovation Center of Quantum Matter,and School of Physics,Peking University,Beijing 100871,China
4Beijing National Laboratory for Molecular Sciences,College of Chemistry and Molecular Engineering,Peking University,Beijing 100871,China
Keywords: quasiparticle band gaps,electron-phonon interactions,basis-set completeness,Beryllium oxide
1. Introduction
Electronic band structures are an intrinsic feature of solids, which determine to a large extent many of their physical properties. Since the 1980s, developments of firstprinciples methods have demonstrated that theGWapproximation within the many-body perturbation theory (MBPT) is an optimal choice in terms of computational cost, theoretical complexity, and computational accuracy for descriptions of the electronic band structures in weakly correlated insulating materials.[1,2]With no empirical inputs,the shapes of the band dispersions and the values of the band gaps can always be well reproduced or predicted.[3]In systems when large discrepancies between theory and experiment exist, such as in ZnO,Jianget al.and Naboket al.have demonstrated that by adding high-energy local orbitals(HLOs)in the all-electron linearized augmented plane waves(LAPWs),[4]the band gap can be increased by 0.91 eV to 3.32 eV.[5,6]The final value is close to the experimental data (~3.4 eV). This indicates that the completeness of the basis set for expansion of the electronic wave functions is still an issue requiring attention. When allelectron methods are chosen, orbitals like HLOs should be considered to address the high-energy electronic states, and their influence on the quasiparticle band gaps should be carefully tested.[5-7]
When this numerical problem is addressed, one can obtain accurate quasiparticle band diagrams at the geometry optimized crystal structures. Beyond this, however,electron-phonon interactions (EPIs) are still absent and they are ubiquitous in condensed matter.[8]These EPIs can be reflected by many properties, e.g., the temperature dependence of the optical spectra,[9,10]the temperature dependence of the quasiparticle band gaps,[11,12]the phonon-limited carrier mobility in semiconductors,[13]the phonon-mediated superconductors,[14,15]and the electron mass renormalization.[16]They are realistic and fundamental in condensed matter physics. To address these EPIs, early theoretical studies often resort to the semi-empirical model Hamiltonian. In the late 1980s and mid 1990s, the advent and developments of density-functional perturbation theory(DFPT)mean that it is possible to study these problems within the first-principles framework.[17-19]Based on this, recently years researchers have witnessed huge progress in the development of theoretical methods on first-principles simulations of the EPIs.[8-11,20-33]However, comparatively speaking, when discrepancies between calculations and experiments exist,the electronic structures methods at geometry optimized structures in further development are often resorted to other than EPIs in standard numerical calculations. Phonon-induced renormalizations of these physical properties are still absent in this paradigm. In many of the existing first-principles calculations of the EPIs,the pseudopotentials(PPs)are chosen due to their low computational cost.These PPs based calculations can suffer from the basis set completeness problem in descriptions of the quasiparticle energies, when special channels are not designed for the high-energy orbitals.[34,35]Besides this, errors due to the pseudoization of the wave functions are also non-negligible.[36,37]These errors decrease when hard PPs with specially designed channels for the high-energy states are chosen.[38]Unfortunately, in most practical calculations,they sum up to non-negligible errors, leading to the fact that benchmark results should still be provided by the all-electron methods with complete basis set. Therefore, to clearly decipher the contributions from each term of interactions to the experimental observed quasiparticle band gaps and optical band gaps, one needs to get the quasiparticle energy with a complete basis set in the all-electron framework. Upon this, the EPIs should be included. Compared to the theoretical results for quasiparticle and optical band gaps obtained with these issues not fully taken care,comparisons between these theoretical results with experiments allow much better understanding of the experimental observations. Taking hexagonal boron nitride(h-BN)as an example,[7]it is an indirect band gap insulator. The quasiparticle energy corrections to the direct/indirect band gaps increased by including HLOs in theGW0calculation are 0.22/0.23 eV.This is far from being negligible. ZPR corrections, on the other hand, decrease them by similar amount(~0.2 eV). Therefore, when the basis set is incomplete and the EPIs are neglected, the final absorption spectrum agrees well with experiment.[39]This fortuitous agreement,however,should not be encouraged. Advances in first-principles methods require that one can control the numerical error in each step of the theory and accurately decipher the contribution from each interaction term to the experimental observations.In this article,we review the state-of-the-art theoretical methods on calculation of the band gaps, focusing on understanding the influence of completeness of the basis set and the EPIs.The article is organized as follows: In Section 2, we present a short overview on the implementation of theGWapproach in the LAPW basis,and analyze the influence of the basis set by adding HLOs. In Section 3, the EPIs are briefly summarized based on MBPT. The electron-phonon matrix elements and self-energy are then introduced, followed by formulas of temperature-dependent band renormalization in both perturbative and non-perturbative methods. In Section 4,applications on bulk wurtzite BeO (w-BeO) and monolayer honeycomb BeO(h-BeO)are given. For w-BeO,including HLOs inGWcalculations widens the band gap by~0.4 eV while ZPR narrows it by similar amount. For h-BeO,the ZPR to the indirect fundamental band gap is?0.37 eV, larger than most typical semiconductors. The conclusions and perspectives are given in Section 5. We use atomic units throughout this article.
2. Quasiparticle energies by including HLOs in the LAPW-based GW approximation
2.1. The G0W0 approximation
The central task of theGWmethod is to obtain the quasiparticle (QP) energiesεQPby solving the QP equation with a non-local self-energy operator. In theG0W0approximation,the non-local self-energy is defined as(in atomic units)



2.2. LAPW basis including HLOs
Now we briefly introduce the basis functions used in the LAPW framework. The LAPW functions can be written as



Another important type of basis in the LAPW framework is the local orbitals (LOs) featuring an extra reference energy,[5,42,44]
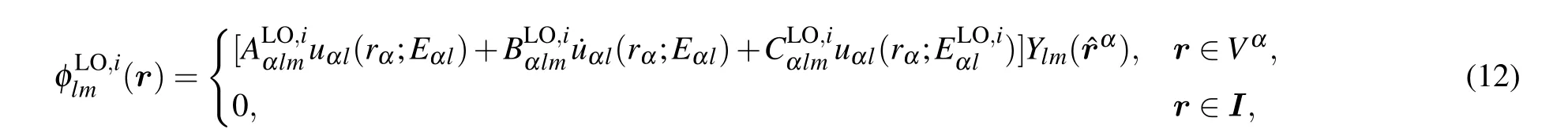


3. Electron-phonon interactions
3.1. Electron-phonon perturbation theory
In the following,before considering electron-phonon interactions,we give the Hamiltonian of the electron subsystem and the ionic subsystem.After that,we derive the formulations of electron-phonon self-energy using many-body perturbation theory.
3.1.1. Electron-phonon matrix elements
The electron subsystem is effectively treated as a noninteracting system based on the KS ansatz,i.e.,Eq.(4). After solving the KS equation, we can rewrite the KS Hamiltonian at a certain ionic configurationRin the second quantization form


whereRIis the position vector of theIth unit cell,ξκα(qν)is the eigenvector.Nrepresents the number of unit cells in Born-von K′arm′an(BvK)supercell, which is the same as the number of Bloch wave vectors in BZ. To go beyond the KS band structure with static nuclei,one can consider the atomic vibration by expanding ?HKSto the second order in the atomic displacement

By using Eq. (20), Eq. (22) can be rewritten in the second quantized formalism as follows:
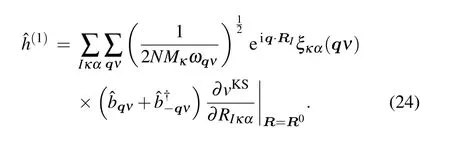
In this case,the second quantized formalism of ?H1can be obtained as


has the lattice periodicity,the matrix in Eq.(25)can reduce to

where

3.2. Electron-phonon self-energy
Based on the Hamiltonian shown in Eq.(33),we use the many-body perturbation theory(MBPT)to obtain the electron Green function and the electron self-energyΣ. Due to the fact that the EPIs are considered mostly at finite temperatures,the Matsubara Green function is resorted to[52]

Compared to Eq.(35),Eq.(38)seeks the trace over a complete set of states of ?H0,denoted as Tr0,which is easier to solve.
By expanding theSmatrix,the numerator of Eq.(38)can be expressed as
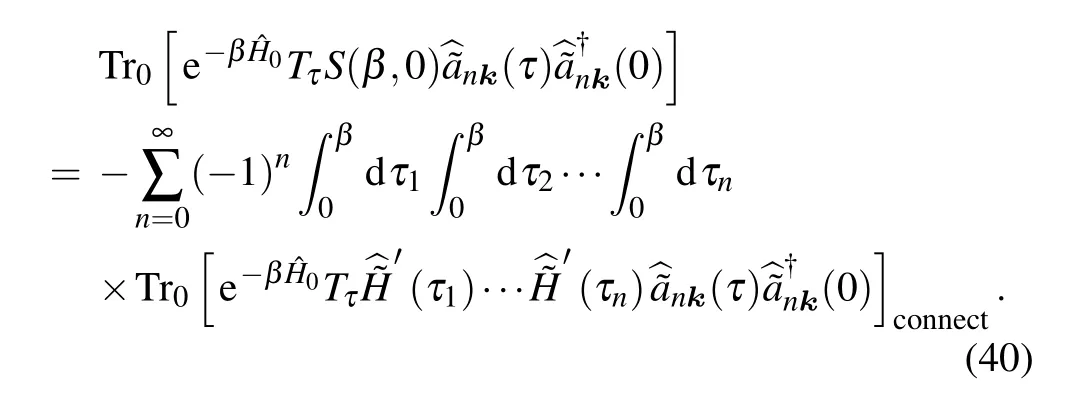
Here, the subscript “connect” means that the diagrams ofSmatrix expansion should only include the distinct connected Feynman diagrams,owing to the fact that the disconnected diagrams have just been canceled by the denominator.
Inserting Eq.(39)into Eq.(40)and applying Wick’s theorem, one can obtain the electron Green function. Specifically, the first-order expansion of the first-order perturbative Hamiltonian yields two electron propagators,one phonon creation operator or one phonon annihilation operator. This term is equal to zero. The second-order expansion of the first-order perturbative Hamiltonian yields three electron propagators and two phonon propagators. This term is nonzero,and the Feynman diagram in frequency-momentum space can be shown in Fig.1.
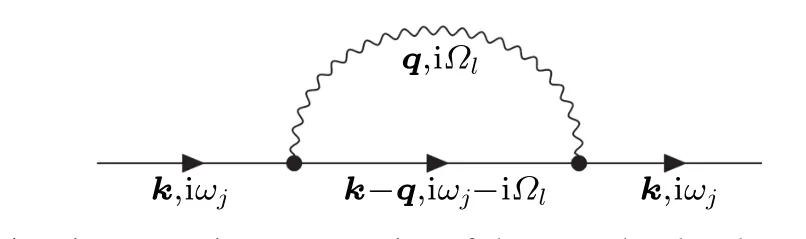
Fig. 1. Diagrammatic representation of the second-order electron Green function corresponding to the first-order perturbative Hamiltonian ?H1.The solid lines represent the non-interacting electron Green function,denoted as G(0). The wavy line represents the non-interacting phonon Green function, denoted as D(0); ωj =(2j+1)π/β is the frequency for fermions,Ωl =2lπ/β is the frequency for bosons,where j and l are integers. The symbol“?”represents the electron-phonon matrix element g.
The electron-phonon self-energy can be obtained by removing the two-sided lines

The superscript“FM” represents Fan-Migdal, due to the following reasons:
For the semiconductors and insulators, within some approximations, this term is referred to the Fan self-energy deduced by the second-order time-dependent perturbation theory by Fan in 1951.[53]
For the metals, this term is referred to the lowest-order electron-phonon self-energy by Migdal in 1958.[54]
The first-order expansion of the second-order perturbative Hamiltonian yields two electron propagators and two phonon propagators. This term is nonzero and the Feynman diagram in frequency-momentum space is shown in Fig.2.
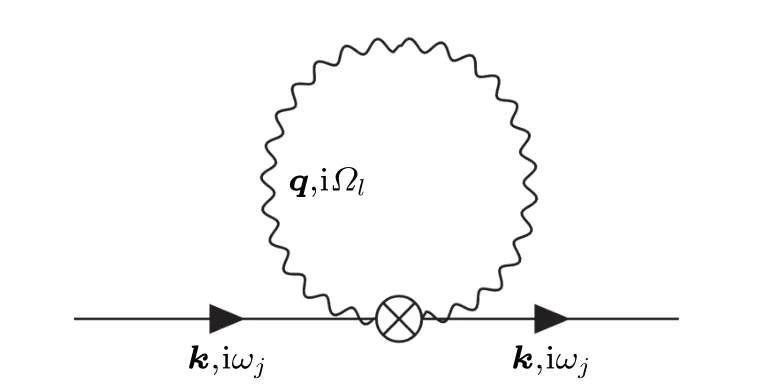
Fig. 2. Diagrammatic representation of the first-order electron Green function corresponding to the second-order perturbative Hamiltonian ?H2. The symbol“?”represents the second-order electron-phonon matrix element g(2).
The electron-phonon self-energy can be obtained by removing the two-sided lines
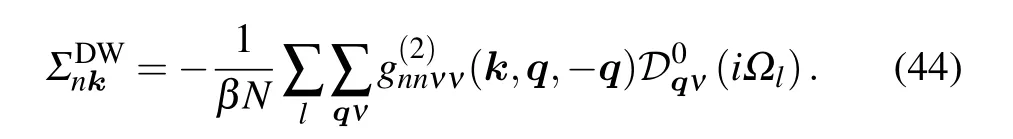
The superscript “DW” represents Debye-Waller, due to the fact that Antonˇc′?k used the pseudopotential modified by the Debye-Waller factor to calculate the temperature-dependent band gaps.[55]
Using the frequency summations,[52]we obtain


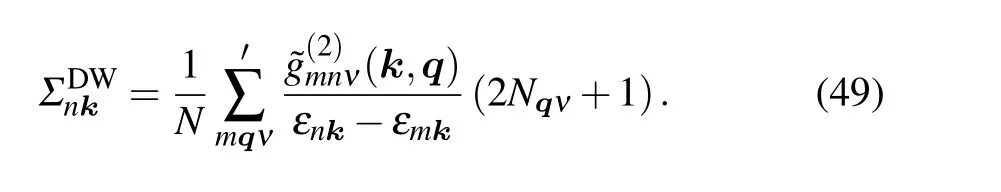
The prime requiresm ?=n. Till now, we have just considered the lowest-order Green function corresponding to ?H1and ?H2. The expansion of Eq. (40), however, is to infinite order.In order to consider the corrections of higher-order terms to the electron Green function, we can combine these two selfenergy diagrams and obtain the Dyson equation. The structure is schematically shown in Fig.3,and the corresponding equation is as follows:
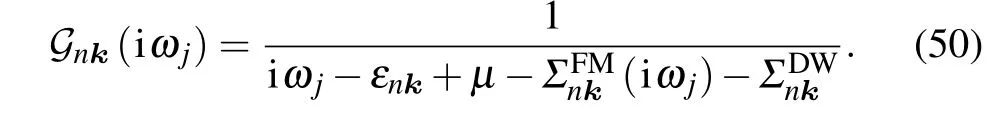
Experimental measurements of excitation energies are for real frequencies. Therefore, one needs to perform analytic continuation of Eq. (50) to the complex plane, and to frequencies close to the real axis. By transforming iω →ω+iδsgn(ω),Eq.(50)is replaced by


Fig.3.Diagrammatic representation of the Dyson equation.The double line represents the dressed Green function,and the single line represents the non-interacting Green function.
Assuming thatGnkhas a pole atEnk+iΓnk ?μ, we can obtain the real part of the quasiparticle energy as follows:


The DW self-energy only shifts the quasiparticle energy,while FM self-energy has a contribution to both the quasiparticle energy and the quasiparticle lifetime. When the renormalization factorZ= 1, it represents the static limit of the quasiparticle approximation, called on-the-mass-shell (OMS)approximation in literature.[27]In the OMS approximation,the FM self-energy is equivalent to the correction to the semiconductor electronic bands by the first-order perturbative Hamiltonian within the second-order time-dependent perturbation theory. Apart from the OMS approximation, allowingεnk ?εmk?q±ωqv ≈εnk ?εmk?q, we can obtain the Allen-Heine-Cardona(AHC)theory,[56,57]
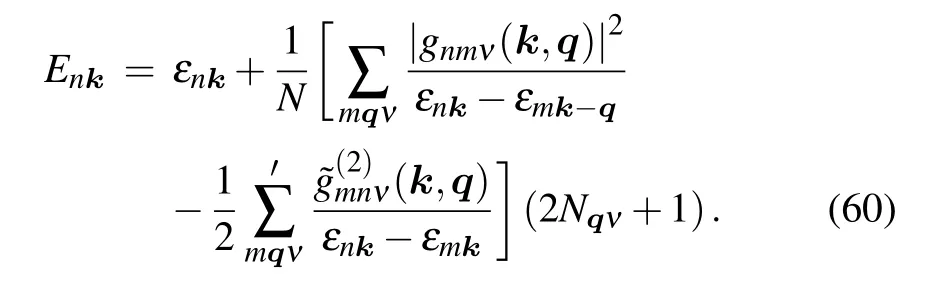
In the history of studies of the semiconductors, researchers used to believe that the FM self-energy is equivalent to the DW term, leading to a misunderstanding to just considering one of them. In 1976, Allenet al.clarified that these two self-energies are inequivalent and of the same order of magnitude.[56]
In the practical first-principle EPIs calculations,the key is to determine the electron-phonon matrix elements. The most popular method is DFPT.[58]The main idea is that the perturbative potential induced by nuclei vibrations leads to the variation of ground-state charge density,which can be obtained by the variation of ground-state electron wave functions. Therefore, one can obtain the variation of the charge density and the effective potential by solving the Sternheimer equation of the Schr¨odinger equation in a self-consistent manner. This method is suitable for the crystal systems with small primitive unit cells, and the electron-phonon matrix elements of any point in the BZ can be obtained. Due to the requirement for dense BZ sampling in EPIs calculations, researchers also developed some interpolation methods, such as Wannier interpolation, which is successfully employed in a number of applications ranging from metal and superconductors to semiconductors and nanoscale systems.[8,22,59]
3.3. Nonperturbative methods
For the system with no periodicity or with large primitive unit cells, the numerical convergence of the electronphonon matrix elements calculation based on DFPT is challenging. One needs to resort to alternative approaches. To make the review complete, we introduce two methods based on the nonperturbative approach in the following discussions,i.e.,the“finite displacement”method and the“ensemble average”method.
3.3.1. Finite displacement
Performing the Taylor expansion of the atomic displacements to the second order within the harmonic approximation,[20]one can reach

The atomic displacements are regarded as perturbation,while the EPIs are not. In practical calculations, a supercell is constructed by the given phonon modes, leading to a set of atomic displacements.[60,61]The second derivatives of the finite atomic displacement corresponding to the electron eigenvalues are calculated by the second-order difference formula.The advantage of the finite displacement method is its simpler algorithm. The disadvantage is the extremely large supercell corresponding to long-wavelength phonons. Recently,nondiagonal supercell was proposed, which can help to reduce the computational cost.[28]
3.3.2. Ensemble average
Ensemble average is another method,which aims to calculate the thermal average of a physical quantity in the adiabatic approximation. The properties are calculated by using a series of the nuclear configurations generated from some sampling methods, such as the harmonic approximation, the molecular dynamic, the path-integral molecular dynamic, or the path-integral Monte Carlo simulations. Taking the electronic band gap as an example, correcting it due to electronphonon interaction using this ensemble average method we have
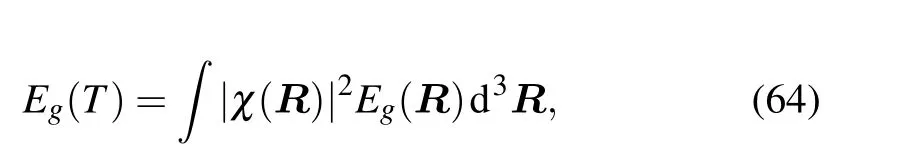
whereχ(R)is the nuclear wave functions.In the harmonic approximation the phonon wave functions can be solved analytically,and the above equation can be simplified by the Gaussian integral[9]
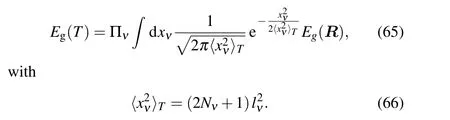
Here,lνis the zero-point vibrational amplitude of theνth mode,Nνis the Bose-Einstein occupation,Rdepends on the normal coordinatexν. More details and applications of this method can be found in Refs.[9,10,62].
4. Applications
4.1. Bulk wurtzite BeO
Using the methods listed,we take beryllium oxide(BeO)as an example to demonstrate how the completeness of the basis set and the inclusion of the EPIs impact on the quasiparticle band gaps. This material is a wide bandgap oxide crystal,whose most stable crystalline phase is of the wurtzite type. Therefore, we label its bulk phase as w-BeO (space group:P63mc)in the following discussions. Here w-BeO exhibits unique properties,such as high melting points,[63]wide band gap,[64-66]high thermal conductivity,[67]and high electrical resistivity,[68]meaning that it has potential for a wide range of applications in optoelectronic devices.[68,69]In recent years, many theoretical calculations[70-73]and experimental measurements[64-66,70]have been performed to investigate its electronic and optical properties. The role of EPIs on the quasiparticle and optical band gaps, however, has never been considered. The fact that they are naturally included in the experimental observations but absent in the theoretical descriptions means that a direct comparison between experiments and these theoretical results is unreasonable. The absence of EPIs in the reported theoretical calculations also means that contrary to experiments,no temperature dependence of these experimental observable should exist.
4.1.1. Quasiparticle band structure
To minimize the artificial effects for comparison of theoretical and experimental results, we use the experimental lattice parameters (a=2.698 ?A,c=4.380 ?A)[74,75]for all the band gap calculations. The DFT calculations were performed by adopting the generalized gradient approximation of the Perdew-Burke-Ernzerhof (PBE) form[76]for the exchangecorrelation potential. The band structure was first calculated at the PBE level. Three codes were used, i.e., WIEN2k,[4]Viennaab initiosimulation package(VASP),[77]and QUANTUM ESPRESSO(QE).[78]The first one is LAPW based and the latter two are PPs based. For the BZ integration, a 1000k-point mesh was used in WIEN2k,and a 6×6×2Γcenteredk-point mesh was used in the VASP and QE calculations. We chose the parameters RMT(Be,O)=(1.4, 1.5) Bohr and RKmax=7.0 for the LAPW basis in WIEN2k. In the VASP and QE calculations,the energy cutoffs were chosen as 800 eV and 70 Ry,respectively. The results are shown in Table 1,consistent with the previous theoretical calculations.[73,79]The value of 7.44 eV in Ref. [79] is due to the fact that different lattice constants were used in their calculations. Our calculations exactly reproduce their value when their lattice constants are chosen.

Table 1. Calculated PBE band gaps (in eV) from three theoretical approaches of w-BeO and compared with others’calculations.
Then we apply the quasiparticle corrections, using theG0W0andGW0approaches. To decipher the impact of the high-energy states in a clean manner, i.e., without artificial effects from other issues like the pseudoization of the wave functions,[36,37]theG0W0andGW0calculations were performed in the all-electron LAPW basis using the GAP2 code.[80]For the frequency dependence of the screened Coulomb interaction, the correlation self-energy was calculated along the imaginary axis and then analytically continued into the real frequency axis by using the multipole fitting scheme, as detailed in Ref. [80]. With standard LAPW basis set,the PBE andGW0band diagram obtained by WIEN2k and GAP2 codes are shown by black and red solid lines in Fig. 4. The smallest direct band gap is atΓ[k=(0,0,0)]from the valence band maximum (VBM) to the conduction band minimum (CBM). The PBE direct band gap is 7.63 eV and theGW0direct band with the standard LAPW basis is 10.45 eV.Then,motivated by recent separate studies of Jianget al.[5]and Naboket al.[6]on the role played by HLOs inGWcalculations, we investigate how theGW0band gaps of w-BeO can be changed by including HLOs in the all-electron LAPW-basedGWcalculations. TheGWresults are converged at 12×12×4k-point mesh, the parameters corresponding to HLOs arenLO=1, andlLOmax=5. The specific values ofGWcalculations with/without HLOs are shown in Table 2.In comparison to theGWcalculation without HLOs, the inclusion of HLOs inGW0calculations shifts down the VBM by 0.67 eV and shifts down the CBM by 0.31 eV. The results are shown by blue solid lines in Fig. 5, compared with the red ones without HLOs. The comparison of the PBE andGW0without/with HLOs electronic band structure calculations based on the LAPW basis are shown in Fig.4,where the fermi energy is set as zero. It is clear that the inclusion of HLOs has a noticeable influence on theGWcorrections, which enlarges the direct band gaps by 0.33/0.36 eV inG0W0/GW0calculations. Consistent with the theoretical results for h-BN in Ref. [7], this highlights the importance of high-energy states for descriptions of the quasiparticle excitations in such wide gap systems.
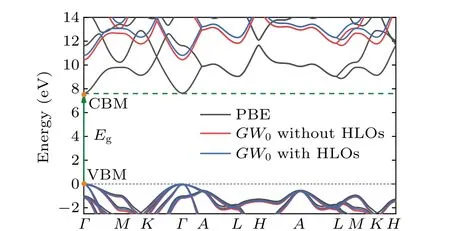
Fig. 4. Electronic band structure calculation by means of the LAPW method showing PBE(black solid lines)and GW0 without/with HLOs(red/blue solid lines)results of w-BeO,where the fermi energy is set as zero(gray dotted line). The green arrow line represents the direct band gap transition.
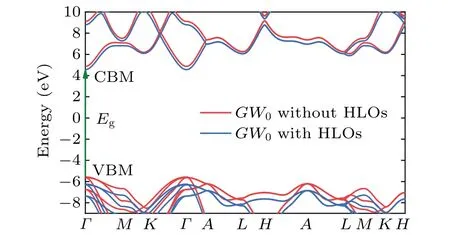
Fig. 5. Electronic band structure calculation by means of the LAPW method showing GW0 without/with HLOs(red/blue solid lines)results of w-BeO.The green arrow line represents the direct band gap transition.

Table 2. Calculated band gaps (in eV) of w-BeO. The influence of HLOs on the GW band gaps and EPI-induced ZPR are highlighted.
4.1.2. EPIs-induced bandgap renormalization
Next,we investigate the EPI-induced band gap renormalizations. This is carried out by using the YAMBO code,[23]with the KS orbitals and eigenvalues generated from the QE calculations. The EPIs were described by using Eq. (58)within DFPT at PBE level. The electron-phonon self-energy was obtained using 1000 randomq-points in the phonon BZ,a uniform 6×6×2k-grid mesh in the electron BZ and 32 electronic bands. In Fig. 6, we show the EPIs induced corrections to the direct band gap of w-BeO. The EPIs-induced correction to the static direct band gap has a weakTdependence below room temperature (300 K) and increases almost linearly beyond it. To figure out the contribution of EPIs to VBM and CBM,we present theT-dependent VBM and CBM renormalizations in the inset of Fig.6. At 0 K,the EPIs shift up the VBM by 0.17 eV and shift down the CBM by 0.23 eV.The ZPR to the direct band gap is?0.40 eV,as shown in the last two columns in Table 2. For most typical semiconductors,such as Si and GaAs,the ZPRs are only about 50-70 meV(see Table 3 in Ref.[81]),which are lower than w-BeO.Hence,the EPIs are strong in w-BeO.

Fig.6. T-dependent direct band gap renormalization of w-BeO calculated by using Eq.(58)within DFPT at PBE level(blue).The zero-point renormalization is ?0.40 eV. The inset shows the T-dependent VBM(black)and CBM(red)renormalizations.
The corrections of HLOs and EPI induced are both large.However, both of them tend to be ignored in practical calculations. When the PPs based method is used for the description of the quasiparticle energies,the former error(due to HLOs)may seem smaller due to contributions from the pseudoization of the wave functions, as detailed in Refs. [36,37].We should note that an in-depth understanding of quasiparticle band gaps from the theoretical perspective requires contribution from each term in the simulations to be accurately described.In w-BeO,the band gap increased by including HLOs inGW0calculation (0.36 eV) is almost equivalent to the one decreased by EPIs (0.40 eV). The cancelation between these two terms results in the fact that the final value is close to the one when both of them are neglected. The large magnitude for both of them means that to get a correct understanding of its band structure,one needs to consider both the effects of HLOs inGWcalculations, and the EPI-induced band renormalization.
4.2. Monolayer honeycomb BeO
As a member of the isoelectronic series of the first-row elements such as graphene and h-BN, studies have predicted that BeO may also exist in an sp2hybridized atomic layer with a honeycomb structure(h-BeO).[82,83]This h-BeO(space group:P63/mmc) has the most stable graphitic phase of wurtzite materials.[84]Theoretical surveys of possible monolayer honeycomb structures of II-VI semiconductors have also shown that h-BeO has a formation energy, comparable to that of its bulk phase.[85]Therefore, this monolayer structure was deemed to be most experimentally achievable among its two-dimensional candidates.[86]Recently, Shihet al.[87]demonstrated the feasibility of growing h-BeO monolayers by MBE, and illustrated that the large-scale growth, weak substrate interactions,and long-range crystallinity,making h-BeO an attractive candidate for future technological applications. Converging the band gap for two-dimensional materials with HLOs included is still technically challenging in GAP2.Therefore,we resort to PBE to demonstrate the key feature of its band structure and focus on EPIs in this part. In optimizing the structure, VASP along with the projector augmented wave(PAW)pseudopotentials was adopted.[88]The optimized lattice constants area0=b0= 2.68 ?A, in good agreement with previous calculation.[89]The band structure calculated by means of the WIEN2k method is shown in Fig. 7. The PBE band gaps are given by three theoretical approaches can be found in Table 3, consistent with the previous theoretical calculations.[89]
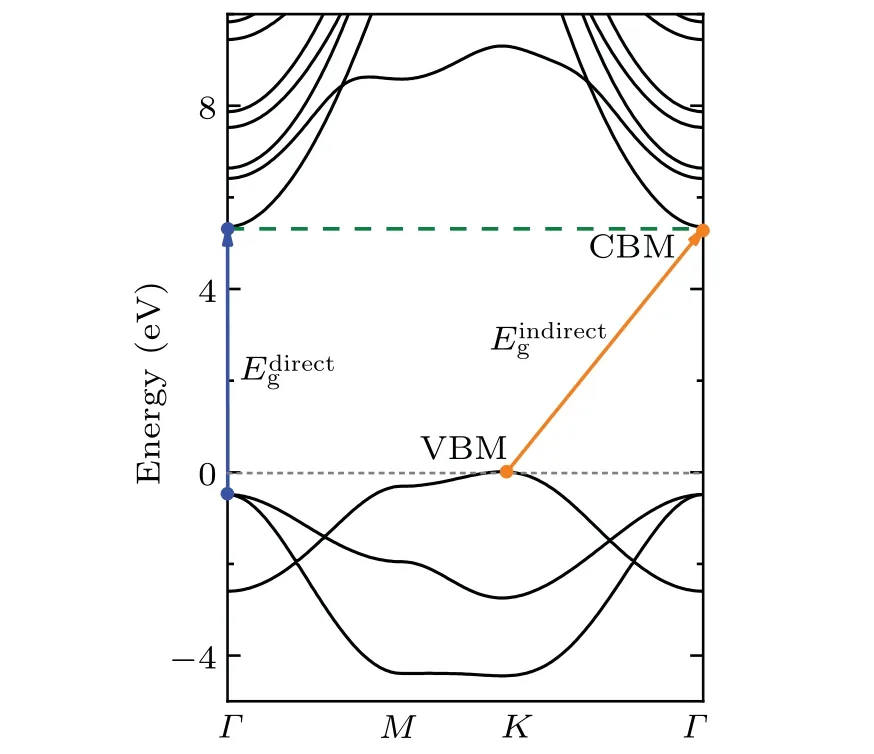
Fig. 7. DFT-PBE electronic band structure calculation by means of WIEN2k method(black solid lines)of h-BeO.The orange(blue)arrow line represents the indirect(direct)band gap transition.

Table 3. Calculated PBE band gaps(in eV)from three theoretical approaches of h-BeO and compared with the others’calculations.
The value of 5.45 eV in Refs.[73,90,91]is due to the different optimized Be-O bond length,which are 1.53,1.525 and 1.524 ?A in their calculations and 1.547 ?A in our calculations.We can obtain the similar values when their lattice constants are chosen. In the electronic structure calculations of h-BeO,we adopted the same parameters as the calculations of w-BeO,except for a 6×6×1Γcenteredk-point mesh in the VASP and QE calculations. Different from the w-BeO bulk phase,this monolayer has an indirect fundamental band gap between the VBM atKand the CBM atΓ.The direct gap atΓis larger.In the EPIs calculations,electron-phonon self-energy was obtained using 32 electronic bands,a uniform 36×36×1q-point mesh in the phonon BZ and the samek-grid mesh for the electron BZ.The ZPR of h-BeO to the fundamental indirect band gap is?0.37 eV (shown in Fig. 8), larger than most typical semiconductors, meaning that the EPIs are equally strong in monolayer h-BeO and in its bulk w-BeO phase. As shown in the inset of Fig.8,EPIs contribute almost equally to VBM and CBM.At 0 K,the EPIs shift up the VBM by 0.21 eV and shift down the CBM by 0.16 eV.
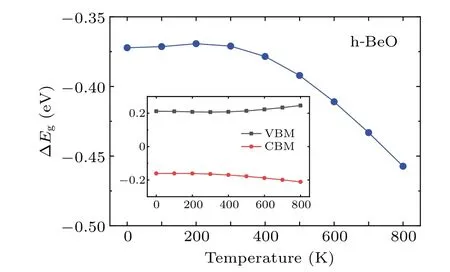
Fig. 8. The T-dependent fundamental indirect band gap renormalizations of h-BeO calculated by using Eq.(58)within DFPT at PBE level(blue). The zero-point renormalization is ?0.37 eV. The inset shows the T-dependent VBM(black)and CBM(red)renormalizations.
5. Conclusions and perspectives
In summary, we have reviewed the theoretical methods for first-principles quasiparticle band structure and EPIs calculations in solids. Including HLOs in the all-electron LAPWsbasedGWcalculations is crucial in getting the quasiparticle band gaps converged. For w-BeO,this widens the direct band gap by 0.33 eV (0.36 eV) in theG0W0(GW0) calculations.Adding in EPI,on the other hand, narrows it by 0.40 eV.For monolayer h-BeO, the EPI-induced ZPR is?0.37 eV for the fundamental indirect band gaps. These values of ZPRs are larger than most typical semiconductors. In w-BeO, corrections from including the HLOs and the EPIs cancel each other.This can explain the fortuitous agreement between experiment and theory when the basis set is incomplete and the EPIs are absent.The phonon-induced renormalization of the band gaps,a term often neglected in practical calculations,is also emphasized by its large magnitude.
Acknowledgement
The authors want to thank Xue-Feng Zhang and Qi-Jun Ye for fruitful discussions.
- Chinese Physics B的其它文章
- Erratum to“Floquet bands and photon-induced topological edge states of graphene nanoribbons”
- Viewing the noise propagation mechanism in a unidirectional transition cascade from the perspective of stability*
- Nonlinear signal transduction network with multistate*
- Optical strong coupling in hybrid metal-graphene metamaterial for terahertz sensing*
- Any-polar resistive switching behavior in Ti-intercalated Pt/Ti/HfO2/Ti/Pt device*
- Magnetic two-dimensional van der Waals materials for spintronic devices*

