Zhaoqiang Ge

Abstract—Necessary and sufficient conditions for the exact controllability and exact observability of a descriptor infinite dimensional system are obtained in the sense of distributional solution.These general results are used to examine the exact controllability and exact observability of the Dzektser equation in the theory of seepage and the exact controllability of wave equation.

I.INTRODUCTION

DESCRIPTOR infinite dimensional system is an important aspect of research for control theory (e.g.,[1]–[15]).It appears in the study of temperature distribution in a composite heat conductor,voltage distribution in electromagnetically coupled superconductive circuits,signal propagation in a system of electrical cables (e.g.,[11]–[14]).There is an essential distinction between descriptor and ordinary infinite dimensional systems (e.g.,[2],[13]–[17]).Under disturbance,not only descriptor infinite dimensional systems lose stability,but also great changes take place in their structure,such as leading to impulsive behavior.

One of the most important problems for the study of descriptor infinite dimensional systems is controllability.Many important results for the controllability of infinite dimensional systems have been obtained (e.g.,[16,Ch.4],[17,Ch.11]).At the same time,many results have been obtained on the controllability of descriptor finite dimensional systems (e.g.,[18],[19],[20,Ch.2],[21,Ch.4]).But the results for the controllability of descriptor infinite dimensional systems are very little.The approximate controllability,exact controllability,and exact null controllability for descriptor infinite systems were studied in [8],[10],[22]–[25],respectively,in the sense of mild solution.The results show that the controllability of descriptor infinite dimensional systems is quite different from ordinary infinite dimensional systems.For example,in the case of infinite dimensional systems,exact controllability is a dual of exact observability.However,according to the direct extensions of the corresponding concepts of ordinary infinite dimensional systems,exact controllability is not necessarily the dual of the exact observability to descriptor infinite dimensional systems in the sense of mild solution.For a descriptor infinite dimensional system,impulse behavior may exist at initial time(e.g.,[2]) which may reduce system performance and even damage the system.In addition,due to the needs of some optimal control problems,the controllability of such systems must be studied.Therefore,we have to deal with the controllability of descriptor infinite dimensional systems in the sense of distributional solution.

In [7],we have discussed the approximate controllability and approximate observability of a class of descriptor infinite dimensional systems in the sense of distributional solution.On the basis of [7],in this paper,the exact controllability and exact observability of a class of descriptor infinite dimensional systems are studied in the sense of distributional solution.Some necessary and sufficient conditions are obtained and dual principle is proved to be true for these two concepts.These general results are used to examine the exact controllability and exact observability of the Dzektser equation in the theory of seepage and the exact controllability of wave equation.Compared with the approximate controllability and the approximate observability,the conditions for the exact controllability and the exact observability are stronger.The research methods of the relevant conclusions are totally different from the approximate controllability and the approximate observability,which need to be solved by new methods.

The descriptor infinite dimensional system

is an abstract form of various partial differential equations and systems,whereL∈L(H1,H2),M∈CD(H1,H2),K∈L(H3,H2),ξ(t) and ζ(t) are state vector and control vector,respectively.Such system generally appears in temperature distribution in a composite heat conductor,voltage distribution in electromagnetically coupled superconductive circuits,signal propagation in a system of electrical cables,motion of ground waters with a free surface,diffusive-convective system with limited manipulating variables,physically meaningful constraints,etc.(see,e.g.,[2],[11]–[14],[26]–[28]).

For convenience of discussion,the following definition is introduced.In the sense of this definition,we will clearly see the essential difference between descriptor and ordinary infinite dimensional systems.

Definition 1:Descriptor infinite dimensional system (1) is called the regular descriptor infinite dimensional system with orderh(positive integer) if there exist Hilbert spacesH21,H22andF∈L(H2,H21×H22),G∈L(H21×H22,H1),whereFandGare bijective,such that

Under these circumstances,operatorsFandGtransfer descriptor infinite dimensional system (1) into the following decoupled descriptor infinite dimensional system on Hilbert spaceH21×H22

From [14,pp.135–138],we obtain that if,Mis a strong(L,q)-radial operator in (1),then descriptor infinite dimensional system (1) is regular descriptor infinite dimensional system with finite orderh,andh≤q+1.

For convenience,here we recall the definitions of (L,q)-radial and strongly (L,q)-radial operators,respectively.

An operatorMis called (L,q)-radial if

In addition,from [14,pp.119–138],we see that many descriptor infinite dimensional systems are regular.Infinite dimensional subsystem (2) is a classical infinite dimensional system in control theory.The properties of descriptor system(3) determine the peculiarities of descriptor infinite dimensional system (1).For example,it is known that controls from the classCh?1([0,+∞),H3) must be used to solve descriptor system (3) in the weak sense (e.g.,[25]).This paper investigates the exact controllability of descriptor infinite dimensional system (1) under some additional hypotheses,or,equivalently,of descriptor infinite dimensional system (2)–(3)and corresponding exact observability.In Section II,the definition of exact controllability of descriptor infinite dimensional system (2)–(3) is introduced.Some necessary and sufficient conditions concerning the exact controllability of descriptor infinite dimensional system (2)–(3) are given by operator theory.In Section III,the concept of exact observability of descriptor infinite dimensional system (2)–(3)is introduced.Some necessary and sufficient conditions concerning this concept are obtained by operator theory.The dual principle of exact controllability and exact observability of the descriptor infinite dimensional system (2)–(3) are given by operator theory in Section IV.In Section V,the general results obtained are used to examine the exact controllability and exact observability of the Dzektser equation in the theory of seepage and the exact controllability of wave equation.Finally,in the last section we summarize our results.

Here we give several auxiliary results.The exact controllability is invariant under system equivalence.Note that every regular descriptor infinite dimensional system is equivalent to descriptor infinite dimensional system (2)–(3),without loss of generality,in the following,we assume that descriptor infinite dimensional system (1) is of the form(2)–(3).

Theorem 1 [2]:Suppose that descriptor infinite dimensional system (2)–(3) is the standard form of a regular descriptor infinite dimensional system with orderh,ζ ∈Ch?1([0,+∞),H3),and there exist constantsc>0,d>0 such that

where exp(Vt) denotes the strongly continuous semigroup generated byV,

where δ(t) is the Dirac function,δ(k)(t) is thek-th derivative of δ(t).For more details of Dirac function,see [29].

It is well known that a mild solution ξ1(t) of infinite dimensional system (2) is expressible forξ10∈H2,ζ∈L2((0,τ),H3)by the formula

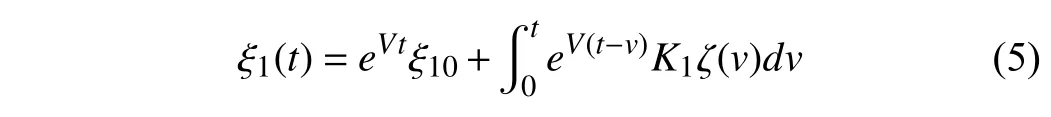
where the integral is understood in the sense of Bochner ([16,pp.104]).

Note that the first line of the matrix in (4),which gives a solution of descriptor infinite dimensional system (2)–(3),is a mild solution of infinite dimensional system (2),while the second line,which is a sum overi,is a distributional solution of descriptor system (3),and

Remark 1:The significant feature of solution (4) of descriptor infinite dimensional system (2)–(3) is that it contains the impulse terms driven by both the initial value of the state ξ and the initial values of the control vector ζ as well as its derivatives even if ζ is sufficiently smooth.For ordinary infinite dimensional systems,this is not possible.

Remark 2:There are strict differences between the mild solution [25]and the distributional solution of system (2)–(3).The main difference is in the expression ofξ2(t).For ξ2(0)∈H22,ζ ∈Ch?1([0,τ],H3),regard the function

as a mild solution of (3).It follows from this that (3) is solvable in the sense of mild solution if and only if the compatibility condition between the right-hand side and the initial data

is satisfied.Therefore,the mild solution of (3) is continuous on [0,τ],while the distributional solution of (3) is discontinuous on [0,τ].

The following is discussed in the sense of distributional solution.

Definition 2:A numberb∈Cis called theL-eigenvalue of the operatorMif there exists a vector ξ ≠0 such thatbLξ=Mξ.Such a vector ξis called theL-eigenvector of the operatorMcorresponding to theL-eigenvaluebof the operatorM.

It is easily verified that theL-eigenvectors of the operatorMcorresponding to sameL-eigenvalue of the operatorMform a subspace ofH1.

II.EXACT CONTROLLABILITY

Consider the descriptor infinite dimensional system described by (2)–(3).The extension of the concept of exact controllability from infinite dimensional systems to descriptor infinite dimensional systems is as follows.

Definition 3:Descriptor infinite dimensional system (2)–(3)is called exactly controllable on [0,τ](for some finite τ>0)if,for any state ξτ∈H21×H22and any initial state ξ0∈H21×H22,there exists a control ζ ∈Ch?1([0,τ],H3) such that the solution ξ(t)∈H21×H22of the descriptor infinite dimensional system (2)–(3) satisfies ξ(τ)=ξτ.

Our purpose here is to establish necessary and sufficient conditions for the exact controllability of descriptor infinite dimensional system (2)–(3) with bounded operatorsK1andK2.

As for the exact controllability of infinite dimensional system (2),we have the following results.

Theorem 2 [16,pp.148]:Infinite dimensional subsystem (2)is exactly controllable on [0,τ]if and only if the following condition holds for somecτ>0 and for all ξ∈H21:

According to Theorem 2,we obtain the following theorem.

Theorem 3:Infinite dimensional subsystem (2) is exactly controllable on [0,τ]if and only if the following condition holds for somecτ>0 and for all ξ∈H21:

g(t)=th(t?τ)h

where .In this case

has bounded inverse.

Proof:Sufficiency.Since,by (8),we have that

Therefore (7) is true.By Theorem 2,system (2) is exactly controllable on [0,τ].

Necessity.Assume (7).If (8) is false,then for any positive integerm,there exists ξm∈H21and ‖ξm‖H21=1,such that

Sinceg2(t) is an increasing function,whent∈[0,τ/2]andg2(t)is a decreasing function,whent∈[τ/2,τ],we have thatg2(t)≥(1/m)1/2[(1/m)1/(4h)?τ]2h,

By (9),we get that

From (7),we obtain that

Asm→+∞,we have that 0 ≥τ2h cτ>0.This contradiction indicates that (8) is true.By [16,Example A.4.2],the inverseis bounded.

As for the exact controllability of descriptor system (3),we have the following theorem.

Theorem 4:Descriptor system (3) is exactly controllable on[0,τ]if and only if

Proof:Necessity.Exact controllability of descriptor system(3) on [0,τ]implies that for any state ξ2τ∈H22and any initial state ξ20∈H22,there exists a control ζ ∈Ch?1([0,τ],H3) such that the solution given by (6) satisfies ξ2(τ)=ξ2τ.Therefore(10) is true.

Sufficiency.Since (10) holds,for any state ξ2τ∈H22and any initial state ξ20∈H22,there existai∈H3,i=0,1,...,h?1,such that.By(6),it follows that,for anyt>0,the corresponding solution is determined only by the value ζ(i)(t),i=0,1,...,h?1.Therefore if a controlζ(t)satisfies

Now,we discuss the exact controllability of descriptor infinite dimensional system (2)–(3).

Theorem 5:Descriptor infinite dimensional system (2)–(3)is exactly controllable on [0,τ]if and only if both infinite dimensional system (2) and descriptor system (3) are exactly controllable on [0,τ].

Proof:The necessity is obvious.We only need to prove the sufficiency.Assume ξ10,ξ1τ∈H21and ξ20,ξ2τ∈H22.We have to find ζ∈Ch?1([0,τ],H3) such that

Thus,(12)is true.Therefore descriptor infinite dimensional system (2)–(3)is exactly controllable on [0,τ].

III.EXACT OBSERVABILITY

In this section,we introduce the dual concept-exact observability.Exact observability is concerned with the ability to reconstruct the state from the system output.Therefore,different from Section II,in this section,the descriptor infinite dimensional system to be considered is following form:

whereF1andF2are bounded linear operators fromH21andH22to Hilbert spaceH4,respectively.The two subsystems of(15) are assumed to be

Definition 4 [16,pp.154]:1) Infinite dimensional subsystem(16) is called exactly observable on [0,τ](for some finite τ>0) if the initial condition ξ1(0) can be uniquely and continuously determined from the output data η1(t) inL2((0,τ),H4).

2) Descriptor subsystem (17) is called exactly observable on[0,τ](for some finite τ>0) if

3) Descriptor infinite dimensional system (15) is called exactly observable on [0,τ](for some finite τ>0) if both infinite dimensional system (16) and descriptor system (17)are exactly observable on [0,τ].

Clearly,Definition 4 reduces to the exact observability in infinite dimensional system theory when the descriptor infinite dimensional system (15) is an infinite dimensional system.By Definition 4,we can obtain the following theorem.

Theorem 6:Let infinite dimensional system (16) and descriptor system (17) be two subsystems of the regular descriptor infinite dimensional system (15).

4) ([16,Corollary 4.1.14]) Infinite dimensional subsystem(16) is exactly observable on [0,τ]if and only if the following c∫ondition holds for somecτ>0 and for all ξ ∈H21:.

5) If descriptor subsystem (17) is exactly observable on[0,τ],then the initial state ξ2(0) can be uniquely determined from the output data η2(t),t∈[0,τ].

6) If descriptor infinite dimensional system (15) is exactly observable on [0,τ],then the initial state ξ(0) can be uniquely determined from the output data η(t),t∈[0,τ].

Proof:Proof of conclusion 5).According to (4),we have

From the linear independencies ofδ(i?1)(t)(i=1,2,...,h?1),we obtain that

if and only ifF2Piξ2(0)=0(i=0,1,2,...,h?1).According to[16,Theorem A.3.61]and (18),we have

Therefore ξ2(0)=0.

Proof of conclusion 6).From (4),we obtain that

By forms of η1(t)and η2(t),we have that η(t)≡0,t∈[0,τ]if and only if η1(t)≡0and η2(t)≡0,t∈[0,τ].Therefore,by proofs of conclusions 4) and 5) of the theorem,ifF1eVtξ1(0)=0 on[0,τ]and (18) is true,thenξ1(0)=0 and ξ2(0)=0,respectively.Hence,the third conclusion holds.

IV.THE DUAL PRINCIPLE

In this section,we deal with the dual principle for regular descriptor infinite dimensional system.Let us first introduce the dual system of a regular descriptor infinite dimensional system in the form of

The two subsystems of descriptor infinite dimensional system (19) are

Definition 5:The following descriptor infinite dimensional system

is called the dual system of descriptor infinite dimensional system (19).

If descriptor infinite dimensional system (22) is the dual system of descriptor infinite dimensional system (19),then the two subsystems of descriptor infinite dimensional system (22)

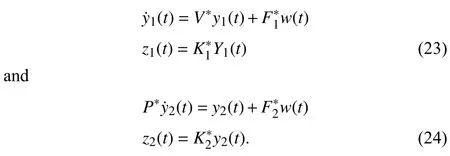
are the dual systems of infinite dimensional system (20) and descriptor system (21),respectively.

The following dual principle reveals the relation between the exact controllability (exact observability) of descriptor infinite dimensional system (19) and the exact observability(exact controllability) of its dual descriptor infinite dimensional system (22).

Theorem 7:Descriptor infinite dimensional system (19) is exactly controllable (exactly observable) on [0,τ]if and only if its dual descriptor infinite dimensional system (22) is exactly observable (exactly controllable) on [0,τ].

Proof:It follows from the Theorems 2,4–6 and Definition 4 that the following equivalence relations hold: The descriptor infinite dimensional system (19) is exactly controllable on[0,τ]if and only if

if and only if the infinite dimensional subsystem (23) and descriptor subsystem (24) are exactly observable on [0,τ]if and only if the descriptor infinite dimensional system (22) is exactly observableon [0,τ].

V.ILLUSTRATIVE EXAMPLES

In this section,we discuss the exact controllability and exact observability of the Dzektser equation in the theory of seepage and the exact controllability of wave equation.

Example 1:Exact controllability and exact observability of the Dzektser equation.

Consider the Dzektser equation describing the evolution of the free surface of seepage liquid (see,e.g.,[26]),

Then,L∈L(H1,H2),M∈CD(H1,H2) and Dzektser equation(25)–(27) can be reduced to the following descriptor infinite dimensional system

We can check that sin(ix)is theL-eigenvector of the operatorMcorresponding toL-eigenvalue?i2(1+i2/(i2?1))of the operatorM(i=2,3,...);

the regular standard form of descriptor infinite dimensional system (28)–(29) is

P=0 in (32),K1ζ=a1ζandK2ζ=a2ζ.

First of all we discuss the exact controllability of descriptor infinite dimensional system (30)–(33).

SinceH22=ran[K2],by Theorem 4,descriptor subsystem(32) is exactly controllable on [0,τ]for any τ>0.It is obviously that the semigroup associated with infinite dimensional system (30) is given by

Since exp(Vt)=exp(V?t),the condition for exact controllability of infinite dimensional system (30) is the existence of acτ>0,such that

It is obviously that nocτsatisfying (34) will ever exist.Consequently,infinite dimensional subsystem (30) is never exactly controllable on [0,τ]for any τ>0.By Theorem 5,descriptor infinite dimensional system (30)–(33),i.e.,Dzektser equation (25)–(26) is not exactly controllable on[0,τ]for any τ>0.

Now we discuss the exact observability of descriptor infinite dimensional system (30)–(33).

Remark 3:According to the definitions of exact controllability and approximate controllability [7]of system(1),we obtain that if system (1) is exactly controllable,then it is approximate controllable.From [7],we have that Dzektser equation in the theory of seepage is approximately controllable.Example 1 shows that it is not exactly controllable.It implies that exact controllability and approximate controllability are totally different.

Example 2:Exact controllability of wave equation.

Consider the wave equation with a distributed controlu(·,t)∈L2((0,1),R)

Then,the following operatorA0onL2((0,1),R) is selfadjoint,positive,and boundedly invertible (see [16,Example A.4.26]):

A proof similar to [16,Example 4.1.8],by Theorem 5,we can obtain that wave equation is exactly controllable.

Remark 4:In reference [22],a class of exact null controllability is introduced,and it is proved that the necessary condition for the solution of the optimal control problem of a class of descriptor infinite dimensional systems is the exact null controllability of the system.It can be seen from [30]that the study of infinite time state regulation generally requires that the system be exactly controllable or exactly null controllable ([25],which is different from the exact null controllability in [22]).Therefore,different optimal control problems have different controllability requirements for the system.

VI.CONCLUSIONS

We have defined exact controllability,exact observability and proved corresponding necessary and sufficient conditions for descriptor infinite dimensional systems.The obtained results are very important and convenient for studying the exact controllabilities and exact observabilities of descriptor infinite dimensional systems.Two examples have been given to illustrate the effectivenesses of Theorems 5 and 6.For a specific descriptor infinite dimensional system,appropriate controllability can be defined according to the needs of various optimal control problems.