LI Lin(李琳),LIN Haichan(林海嬋),OU Yigui(歐宜貴)

(School of Science,Hainan University,Haikou 570228,China)

Abstract:In this paper,we further study the existing supermemory gradient-type method for solving convex constrained monotone nonlinear equations and establish its sub-linear convergence rate under some mild conditions.Furthermore,a more general algorithmic framework of derivative-free projection method for solving convex constrained nonlinear monotone equations is proposed and its convergence properties are discussed.Two illustrative examples are reported to verify the feasibility of the proposed algorithmic framework.

Key words:Nonlinear equation;Monotonicity;Projection method;Analysis on convergence rate

1.Introduction

Step 5 Setk:=k+1,and go to Step 1.

Preliminary numerical results and related comparisons in[8]show that the SGM algorithm is efficient and can be applied to solve some large-scale nonsmooth equations.However,the authors only analyzed the global convergence of SGM,while the convergence rate of SGM was not discussed in theory.As is well known,the convergence rate is also important for an optimization algorithm.In fact,most of the existing derivative-free projection methods for the problem(1.1)only discuss their global convergence,while the convergence rate is not analyzed.[1?3,6]Furthermore,even for those algorithms in which the convergence rate has been analyzed,the obtained result is only about the convergence rate of the distance sequence{dist(xk,X?)},not about the iterative sequence{xk}itself.[4?5]So far,the study on the convergence rate of sequence{xk}is relatively fewer.[7]These facts motivate us to further explore the convergence rate of those derivative-free projection methods for the problem(1.1),which is the motivation behind the present study.

Under the local error bound condition which is weaker than nonsingularity,Yamashita and Fukushima[9]showed that the Levenberg-Marquardt method has quadratic convergence for unconstrained nonlinear equations.Subsequently,this condition has been employed to study the convergence rate of some optimization methods.[4?5,7,10]

Motivated by the above observations,in this paper,we study the convergence rate of SGM,based on the ideas of[7,9-10].Then we further give a more general algorithm framework of derivative-free projection method for solving the problem(1.1)and discuss its convergence property.

The rest of this paper is organized as follows.In Section 2,we summarize some basic definitions and results that will be useful in the subsequent sections.Section 3 is devoted to analyze the convergence rate of SGM under the local error bound condition.In Section 4,a more general algorithm framework of derivative-free projection method for solving convex constrained nonlinear monotone equations is proposed and its convergence property is analyzed.In Section 5,numerical experiments are reported to verify the feasibility of the proposed algorithmic framework.Some conclusions are summarized in the final section.

2.Preliminaries

3.Convergence Rate Analysis of SGM

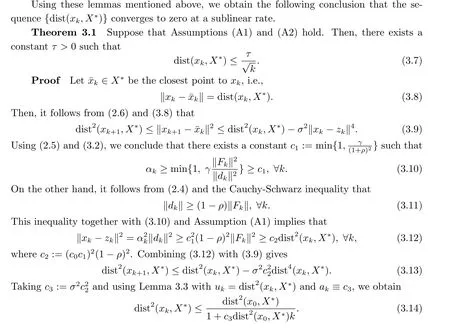
4.Further Discussion

5.Numerical Experiments

Tab.5.1 Numerical Results of Example 5.1

Tab.5.2 Numerical Results of Example 5.2

Based on the numerical results in Tab.5.1 and Tab.5.2,we see that the proposed model UAF is feasible,which shows the truth of theory results proposed in the paper.

6.Conclusion

In this paper,the convergence rate of SGM for solving a class of large-scale nonlinear monotone equations is discussed under mild conditions.Furthermore,a more general algorithm framework of derivative-free projection method for solving convex constrained nonlinear monotone equations is proposed,and the Q-linear or sub-linear convergence rate of the proposed algorithm framework is also analyzed under common conditions.Numerical experiments are also reported to verify the feasibility of the proposed algorithm model UAF.