Kaiyong He(何楷泳) Xiao Geng(耿霄) Rutian Huang(黃汝田)Jianshe Liu(劉建設(shè)) and Wei Chen(陳煒)

1School of Integrated Circuits,Tsinghua University,Beijing 100084,China

2Beijing National Research Center for Information Science and Technology,Beijing 100084,China

3Tsinghua University Future Chip Technology Advanced Innovation Center,Beijing 100084,China

Keywords: quantum computation,quantum simulation,superconducting qubit

1. Introduction

In recent years, superconducting quantum computation and simulation have developed rapidly,which have entered the noisy intermediate-scale quantum(NISQ)era.[1]In the NISQ era,50–100 qubits without error correction can perform some tasks that demonstrate the superior ability of quantum computers. Quantum supremacy has shown that in some tasks,quantum computer could surpass the most powerful classical computers.[2]Another most anticipated application in the NISQ era is quantum simulation,such as exploring many-body quantum physics,quantum chemistry,and so on.[3]However,quantum devices still suffer from noise, and the sizes of the circuits are limited.

In this paper, we focus on some important heuristic advances in the field. In Section 2, basic concepts of superconducting qubits as well as their operation and readout are introduced. In Section 3,experimental realization without error correction of some quantum algorithms, including Deutsch–Jozsa(D-J)algorithm,Grover algorithm,Shor algorithm,and Harrow–Hassidim–Lloyd (HHL) algorithm are summarized.A brief introduction of quantum error correction methods including the Calderbank–Shor–Steane codes (CSS) codes, the surface codes,and Bosonic quantum codes are discussed,followed by a review of two different kinds of quantum simulations,digital and analog quantum simulations,in Section 4.

2. Superconducting qubit

2.1. Three basic types of superconducting qubits

There are three types of basic superconducting qubits,i.e.,the charge qubit,the flux qubit,and the phase qubit,classified according to the “controlled variable”, i.e., the qubit variable for manipulating quantum information.[4]The key element in a superconducting qubit is the Josephson junction,which is a non-dissipative and strongly non-linear superconducting device.Its behavior can be described by the Josephson equation

whereIcis the critical current of the Josephson junction andΦ0=h/2eis the flux quantum. In general, the Hamiltonian of a circuit could be represented with “node voltage”Vand the conjugate “node current”I. However, for a circuit with Josephson junction, a representation based on “node flux”Φand “node charge”Qwould be much more convenient,[5,6]where

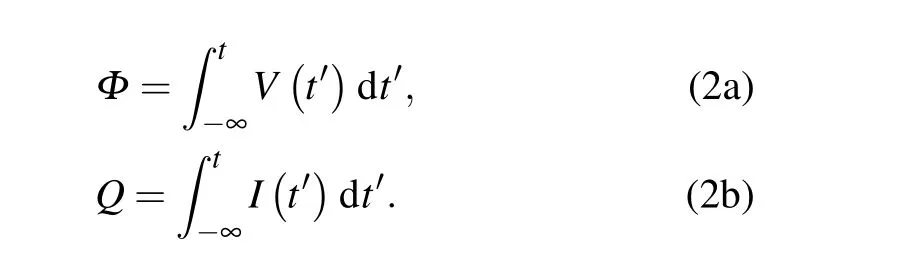
2.1.1. Charge qubit

The basic schematic of a charge qubit, also named as Cooper-pair box,[7,8]is shown in Fig. 1, where a Josephson junction is connected to a small superconducting island and a large superconducting reservoir, while the voltage source controls the charge offsetng=CgVg/2eon the island capacitively.[8]

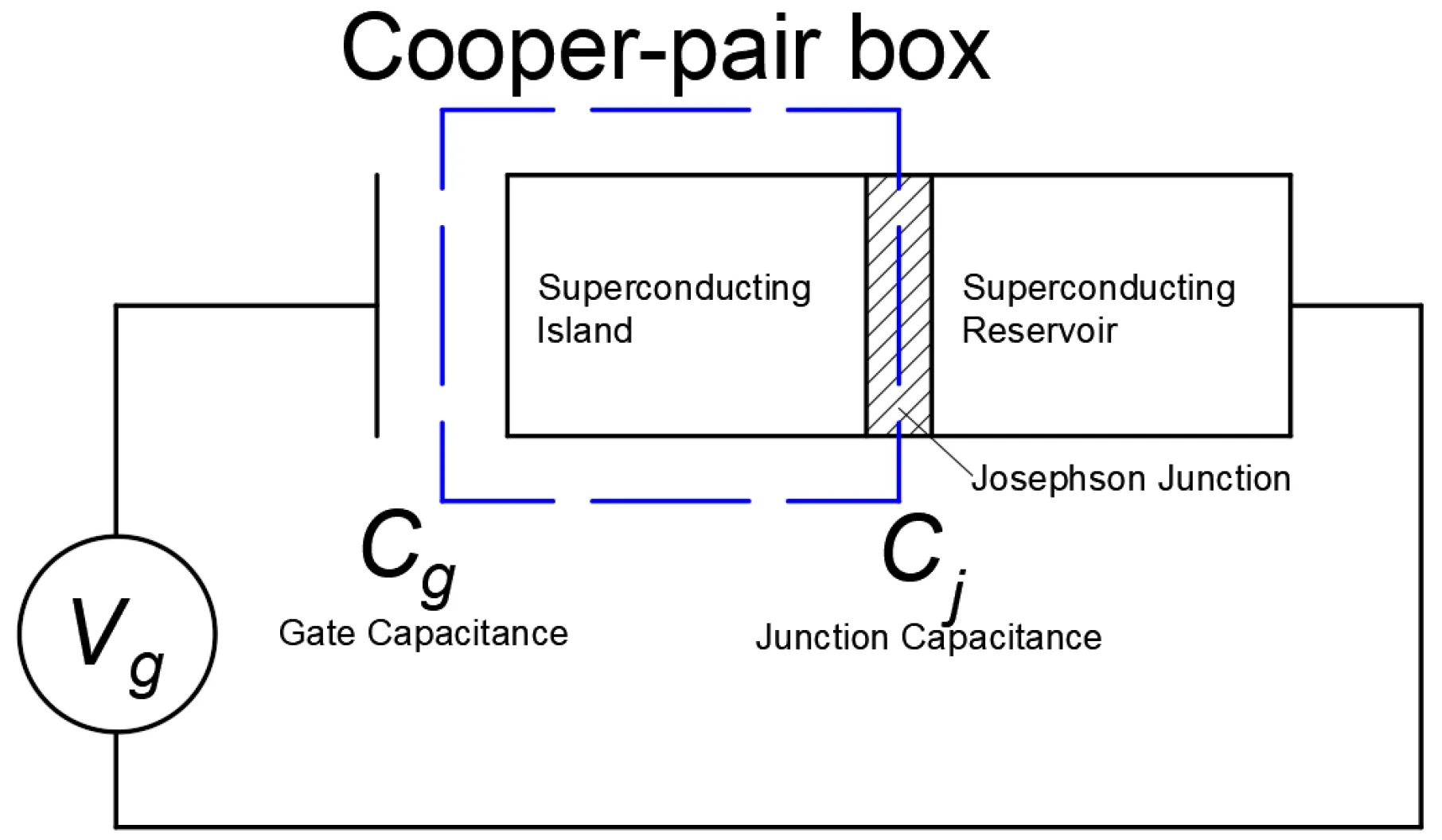
Fig.1. Schematic of the single Cooper-pair box.

The Hamiltonian of the system is

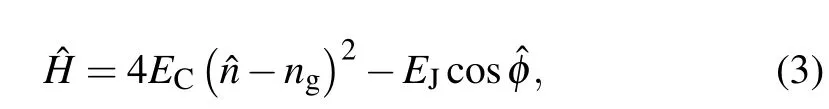
In the so-called charge basis,[4]?n= Σnn|n〉〈n|, and cos ?φ=1/2·Σn(|n〉〈n+1|+|n+1〉〈n|),the Hamiltonian can be written as

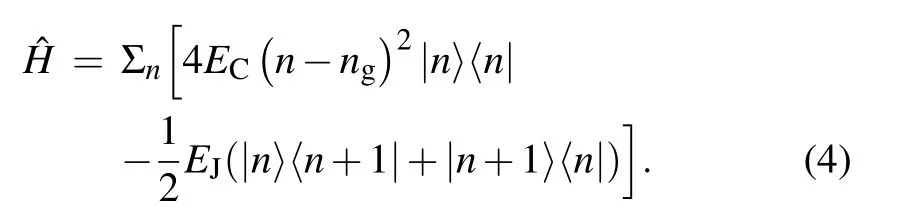
The charge qubit is typically biased at the “sweet spot”ng≈1/2. At the spot,for states|n〉and|n+1〉,the first term of the Hamiltonian is degenerate while the degeneracy is broken by the second term. The two lowest-energy levels are far separated from the others whenEJ?ECsuch that they could form a qubit. In addition,the transition frequency of the system is insensitive to the offset-charge noise to the first order at the sweet spot,leading to a longer coherence time. However,EJ/ECcannot be too small,or the high order of offset-charge noise will be significant.

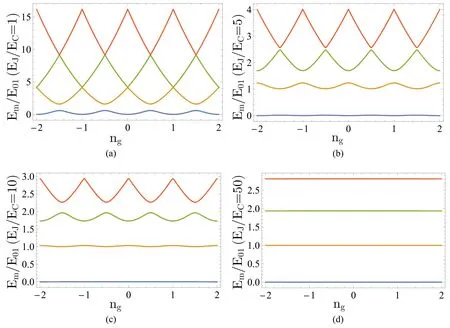
Fig.2. Eigenenergies of Cooper-pair boxes changed by charge offset ng on the gate for different ratios EJ/EC.

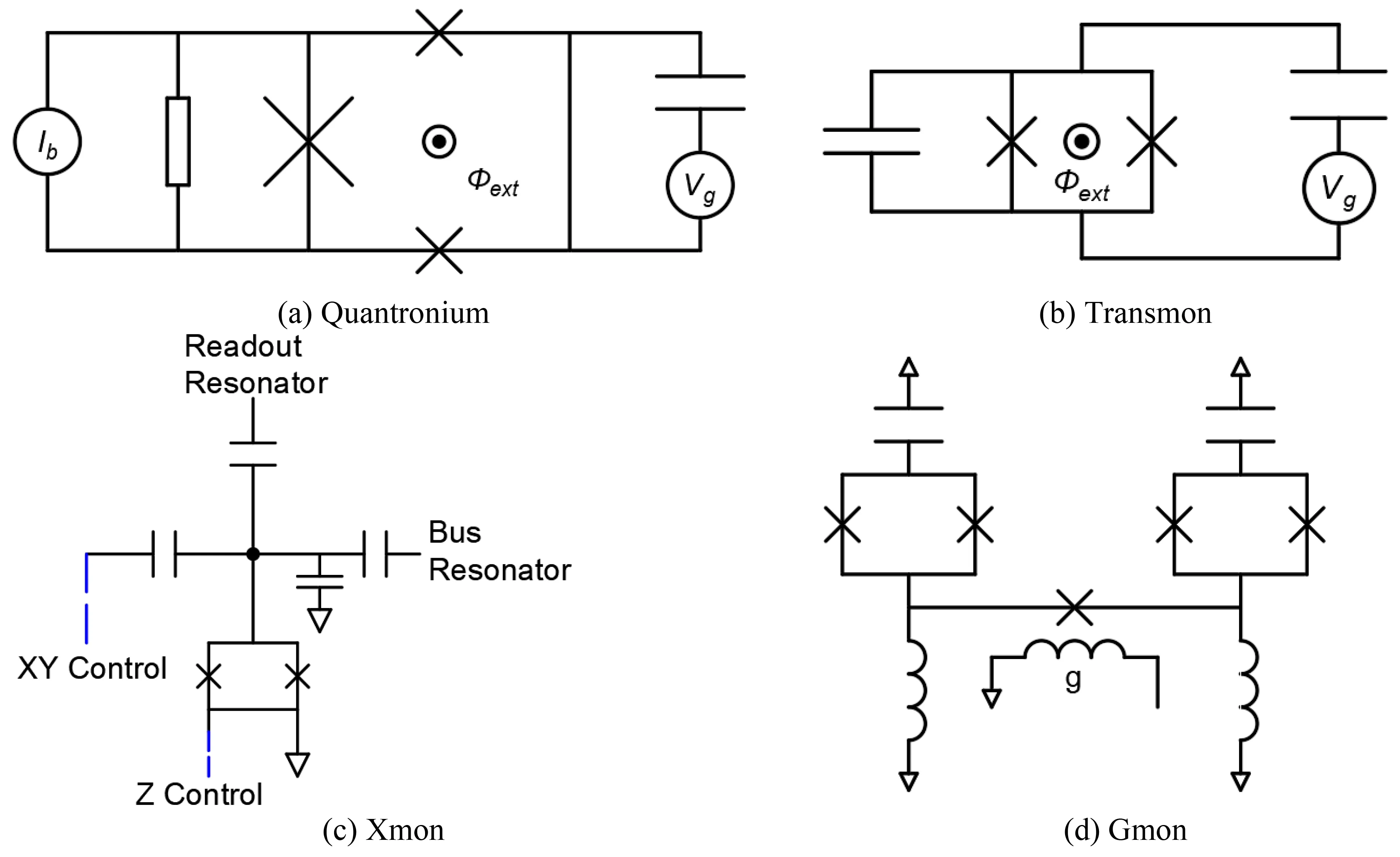
Fig.3. Improved qubits based on charge qubits.

There are some improved qubits based on charge qubit for longer coherence time,easy connectivity,fast control,and high-fidelity readout. The first significantly improved qubit is the “quantronium”[9,10]which is shown in Fig. 3(a). It is a three-junction circuit in which two small junctions define the Cooper pair box coupled to the write and control port and a large junction is coupled to the readout port. The coherence time is improved by two orders of magnitude to hundreds of nanoseconds compared to the basic charge qubit whose coherence time is about 1 ns.

Another important improvement of charge qubit is called“transmon”[11](transmission-line shunted plasma oscillation qubit). A large capacitor is shunted to the charge qubit to increase the ratioEJ/ECproperly, as shown in Fig.3(b). Since the sensitivity to the offset-charge noise reduces exponentially with the increase ofEJ/EC,while the anharmonicity only deteriorates by a weak power law,the advantage dominates. The coherence time of the qubit is increased to tens of μs. The transmon is embedded in a transmission line, which makes control and readout very convenient.A new qubit design based on transmon is Xmon,[12]shown in Fig. 3(c) that has a cross shape structure.Two of the arms are forXYcontrol andZcontrol.The arm coupling to a resonator is for readout and the last arm can couple to other qubits. In such a schematic, the operations,readout and coupling are all convenient and efficient.A Josephson junction can be added between two Xmons to get fast tunable coupling,high coherence,and minimal cross talk,as shown in Fig. 3(d), which is called Gmon.[13,14]In recent years, qubits based on charge-qubit have developed rapidly,showing their potential in quantum computation.

2.1.2. Flux qubit

A flux qubit consists of a superconducting loop interrupted by one or more Josephson junctions, as shown in Fig.4(a).[15–17]It can be considered as the dual of the charge qubit,and the Hamiltonian of the circuit can be written as

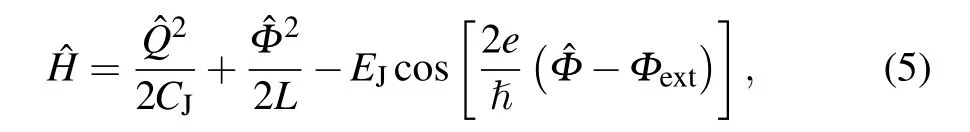
whereΦextrepresents the external applied flux through the superconducting loop. From the Hamiltonian, one can see that the potential of the flux qubit is composed of a parabolic potential and a cosine corrugation. The typicalEJ/ECvalue of a flux qubit is about 50,and thus ?Φis a good quantum number and charge has large fluctuation. However, in different kinds of flux qubits, theEJ/ECvalue can vary considerably (from tens to thousands),and the main feature of a flux qubit is that its controlled variable is the flux.[15–22]

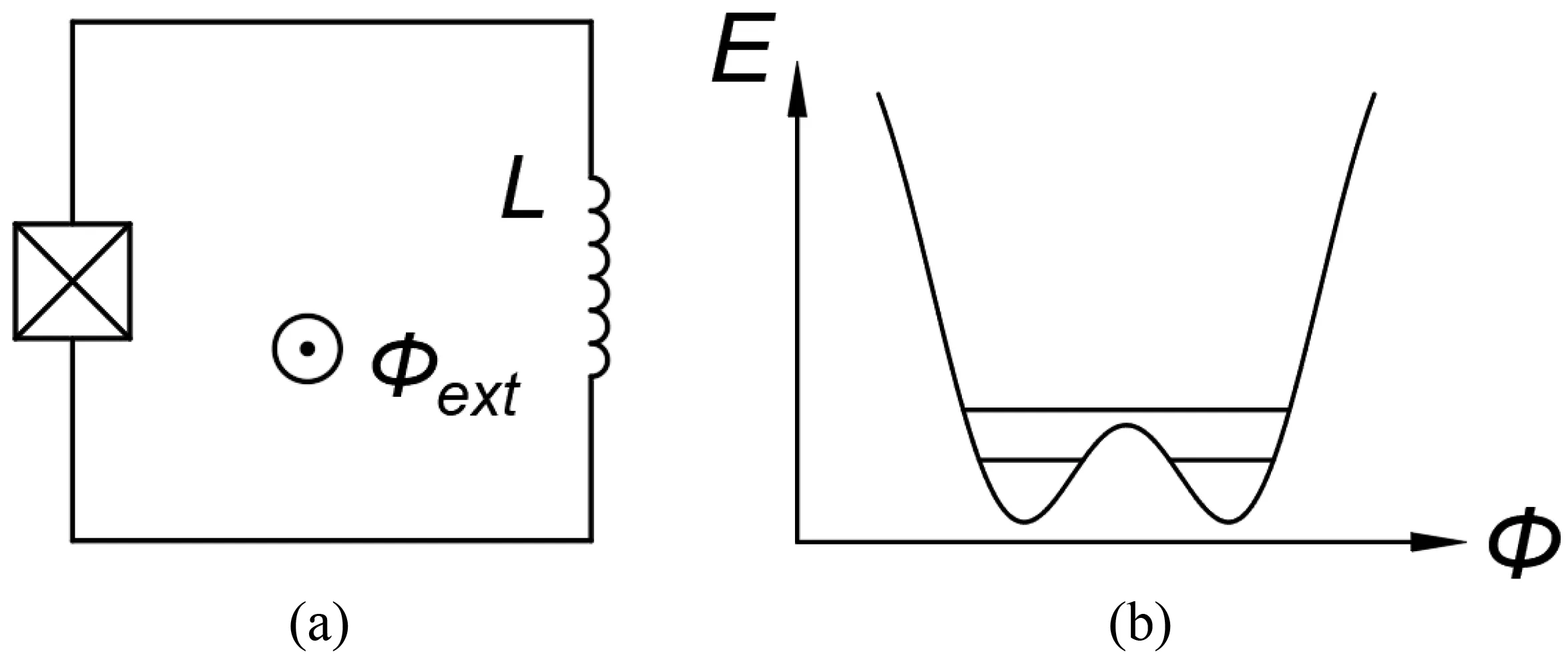
Fig.4. Flux qubit.

The general feature of the potential of a simple flux qubit is shown in Fig. 4(b). WhenΦext/Φ0≈0.5 and in the twolevel approximation,the qubit Hamiltonian is given by

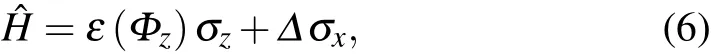
whereεis the energy difference between the bottoms of two wells,a function of flux through the superconducting loop(denoted asΦz),and?is the tunneling-coupling strength between the two current states. Replacing the Josephson junction with a dc-SQUID loop,the qubit Hamiltonian becomes

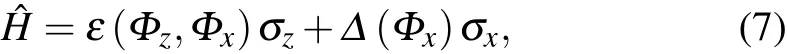
whereΦxis the externally applied flux through the SQUID loop, as shown in Fig. 5.εis not only a function ofΦz, but also ofΦx,and?becomesin situtunable now. Thus,the flux qubit is a spin-1/2 system with tunablezandxfields, which is also a proper building block for quantum annealing applications based on the transverse Ising Hamiltonian.

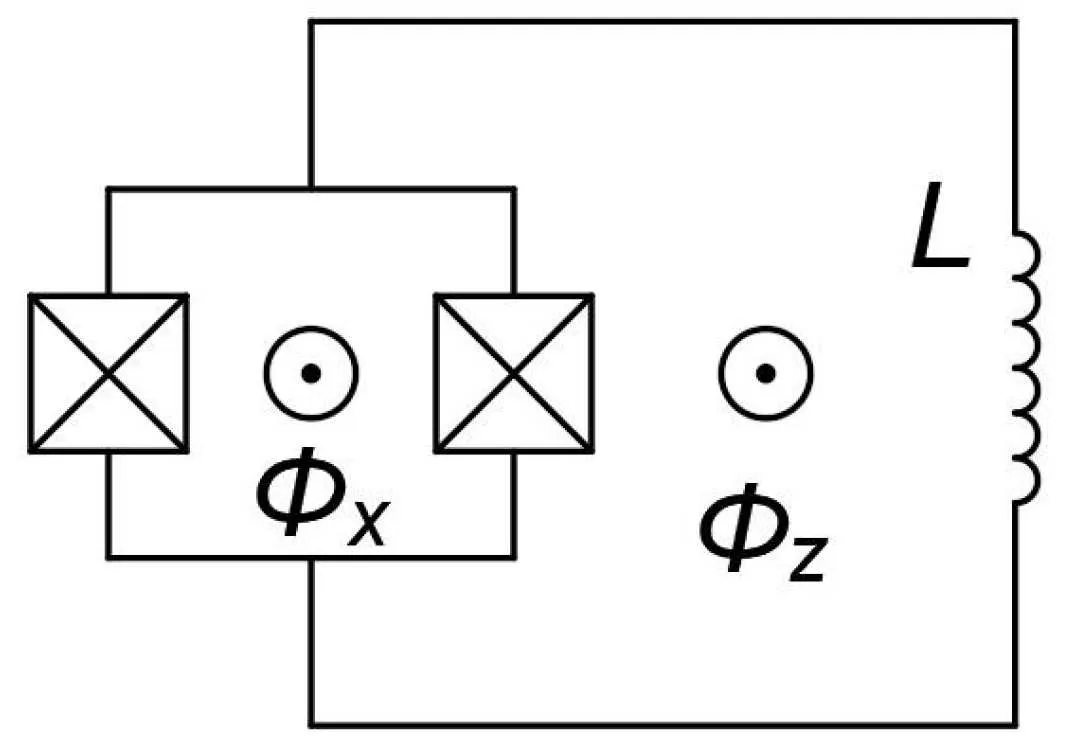
Fig.5. Flux qubit whose Josephson junction is replaced by a dc-SQUID.

In general, a flux qubit needs a large self-inductance,which can be achieved with a large loop size to satisfy the flux quantization condition. However,a large loop will introduce more flux noise to the flux qubit,limiting the coherence time. A better choice is to put 3 junctions in the loop,[16,17]as shown in Fig. 6(a), in which the loop size is reduced and the flux quantization condition is satisfied by introducing two large Josephson junctions in the superconducting loop.

To reduce the sensitivity to charge noise and improve the device-to-device reproducibility, a large capacitor could be shunted to the smaller junction in the 3-junction flux qubit,resulting in a “capacitively shunted flux qubit”, whose coherence time is in the range of 50 μs to 100 μs.[18–20]The schematic of such a C-shunt flux qubit is shown in Fig. 6(b).Another efficient way to reduce the influence of offset-charge noise is to shunt the small junction with a series array of largecapacitance tunnel junctions,resulting in a fluxonium,[21,22]as shown in Fig.6(c).

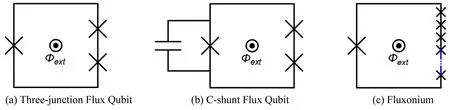
Fig.6. Improved qubits based on flux qubits.

2.1.3. Phase qubit

The third basic type of superconducting qubits is the phase qubit,[23–27]which consists of a dc-current-biased Josephson junction,as shown in Fig.7.Its coherent oscillation was observed in 2002.[23,24]The controlled variable of a phase qubit is the gauge-invariant phase ?φ=2π?Φ/Φ0. Since the ratioEJ/ECis about 106,the good quantum number is the phase ?φ, and is insensitive to the offset-charge noise. The Hamiltonian of the circuit is

There is a built-in readout in the phase qubit. When sending a probe signal to induce a transition to the higher level from|1〉state, the tunneling probability through the potential well will increase rapidly. After tunneling, the phase runs down the washboard,leading to a voltageV/=0 appearing across the junction, which implies that the qubit was in state|1〉. If the qubit was in state|0〉,the voltage keeps zero.

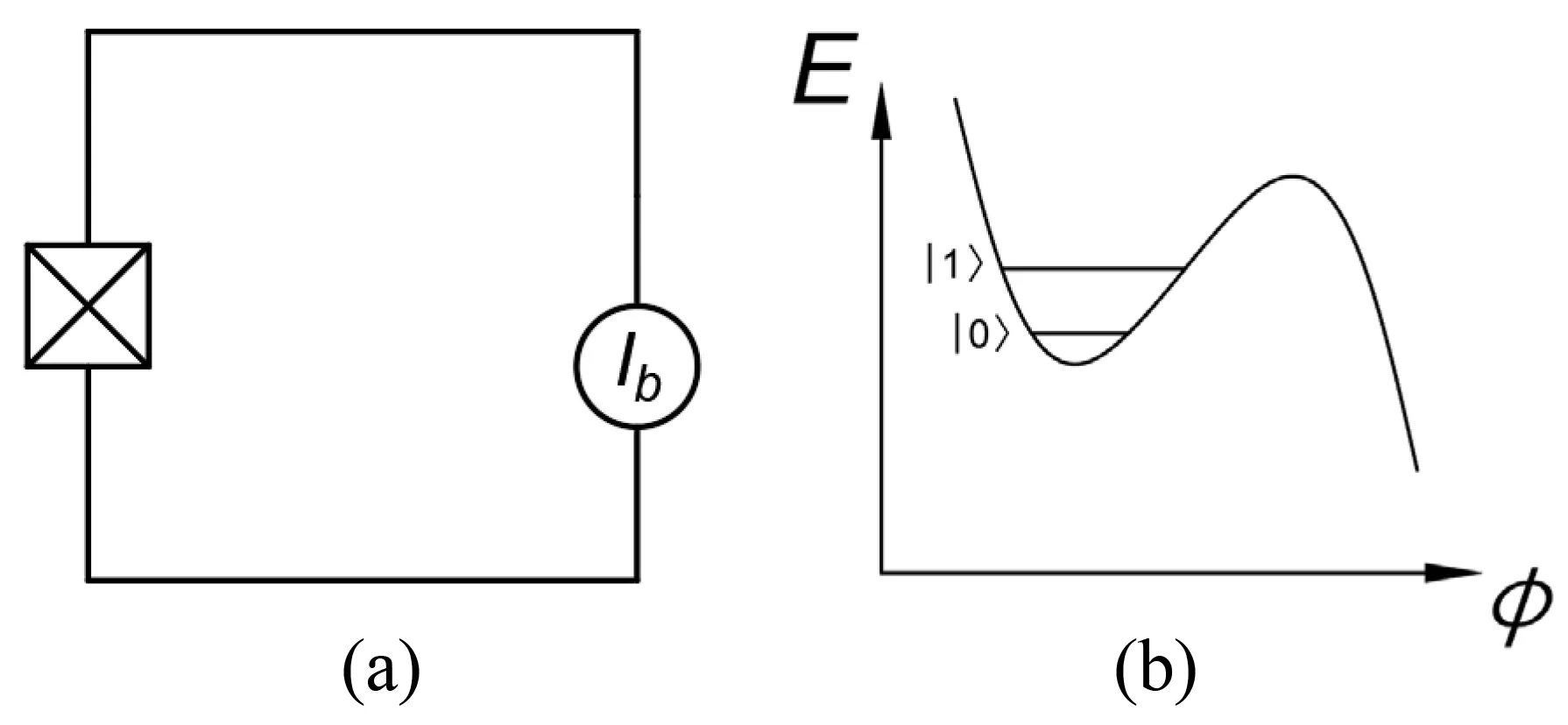
Fig.7. Phase qubit.

When biasing the qubit with current, the qubit will dissipate strongly from the bias lead. An improved method is to bias the qubit with a magnetic flux.[23,28]It transforms the impedance,and thus provides isolation of the phase qubit from the environment. There is also a significant modification in the readout of phase qubit.[29,30]If the phase qubit is readout from voltage, quasiparticles are generated when the junction switched into the voltage states. They are found to influence the decoherence of the qubit.A better design is to readout with a SQUID separated from the qubit. The change of the circulating current in the qubit loop, which is generated from the tunneling event, can be probed with the SQUID. The quasiparticles generated during the readout are kept away from the qubit,and thus increasing the decoherence time.

2.1.4. Other kinds of superconducting qubits

There are some other kinds of superconducting qubits.0-πqubit is a qubit whose logical states are disjoint support so that it is exponentially protected from charge (flux)noise.[31,32]Quasicharge qubit exhibits the characteristics of the artificial atom which is dual with transmon.[33]The exploration of new kinds of qubits is still in progress,and the family of superconducting qubits is being broadened. With decades of development, the performance of superconducting qubits has increased gradually. Table 1 shows the decoherence time of superconducting qubits reported in recent years.

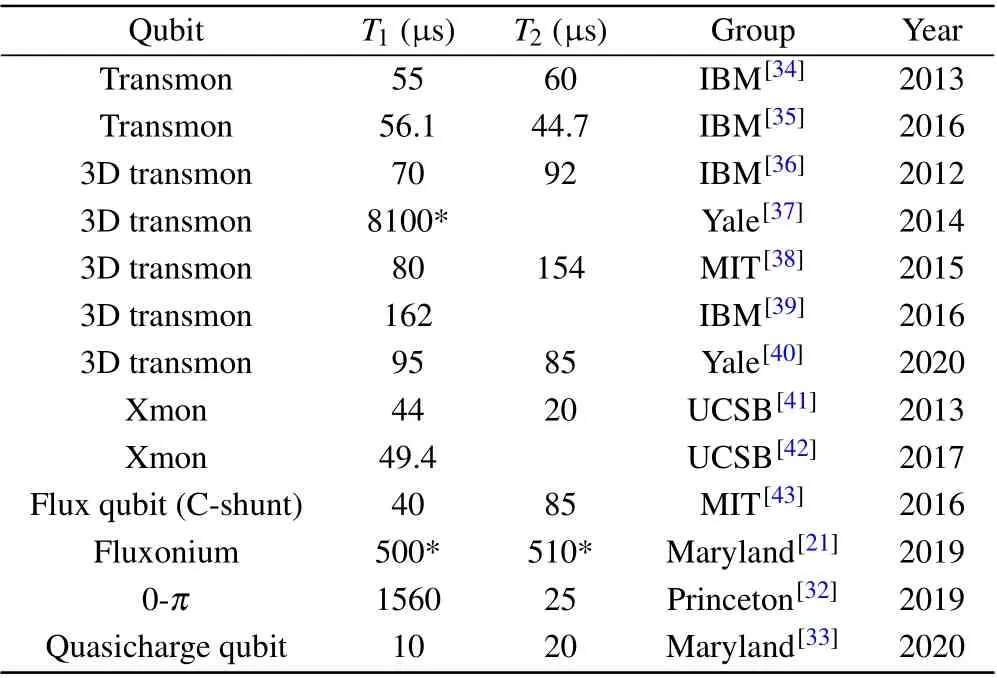
Table 1. Decoherence time of superconducting qubits.

2.2. Gate operations

The gate operations and readout of superconducting qubits are implemented by applying microwave pulses,which could be described by circuit quantum electrodynamics(circuit-QED).[44,45]Usually, the qubit is coupled to a resonator and with microwave pulse applied to the resonator,one can realize gate operations and readout of the qubit. Under rotating wave approximation (RWA), the Hamiltonian of the coupled system is situations. According to the last term,we could see that when the qubit is populated to the excited state,a photon is annihilated in the resonator, and while the qubit drops back to the ground state,a photon is created in the resonator. In this process, energy is conserved. In the following section, based on the Xmon qubits,we will discuss how to perform gate operation and readout on the qubits.

2.2.1. Single qubit operations

For Xmon,rotation in theXYdirection is achieved by applying microwave via the waveguide on the left, as shown in Fig.3(c).[47]Assuming that the microwave is[44]

We can see that the total effect of phaseφ0is to perform a rotation alongzaxis byφ0. Since our readout is along thezaxis,the lastz-rotation does not matter.Consequently,a virtualZgate is achieved. The other conventional method to performZgate is to tune the frequency of Xmon by adjusting external flux in the SQUID of the qubit. The Hamiltonian of the Xmon could be written as

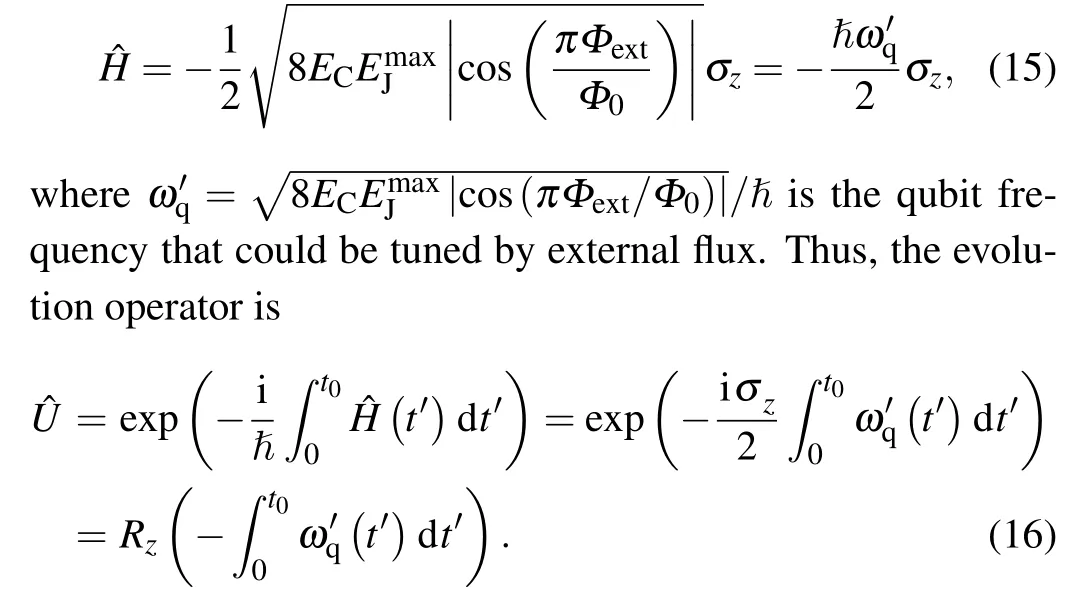
By tuning the frequency carefully, an arbitrary angle rotation alongzaxis could be achieved. Since any rotation on the Bloch sphere could be decomposed into 3 rotations,R(α,β,γ) =Rz(α)Ry(β)Rz(γ), all the single qubit operations could be achieved. Moreover, the rotation can be accomplished along only two axes, which would simplify the implementation at the hardware level.[49]

2.2.2. Two qubit operations

As we know, a small gate set composed of single qubit gates and a two-qubit gate,iSWAP gate. ControlledZ(CZ)gate,which is also denoted as controlled phase (CPHASE) gate, and cross-resonance (CR)gate are other two types of important two-qubit gates. With these gates,the universal quantum computation without errorcorrection could in principle be achieved.

It swaps the excitation between two qubits with an additional phase. With some single-qubit gates and iSWAP gates, one can generate a CNOT gate,[51,52]as shown in Fig.8.

Fig.8. CNOT gate generated from iSWAP gate.

When operating superconducting qubits only with the lowest two energy levels, higher energy levels should be avoided because they tend to deteriorate the performance of a qubit. However,for the case of transmon qubits, the higher energy levels can be used to generate CZ gates.[53]The CZ gate is often implemented by adiabatic tuning.[41,54]In recent years,some high fidelity non-adiabatic CZ gates are also realized.[55,56]Combining a CZ gate and two Hadamard gates,the CNOT gate can be generated,as shown in Fig.9.

CR gate is an all-microwave two-qubit entangling gate for qubits whose frequencies are not tunable.[57–59]When the target qubit is applied by microwaves that are resonant with the control qubit, the coupling interaction turns on. Since such qubits are not flux-tunable,it is less sensitive to the flux noise, which leads to longer decoherence time. Combined with single-qubit gates, the CR gate can also relate to the CNOT gate.[44,58]

Table 2 summarizes the fidelities of state-of-the-art twoqubit gates of superconducting qubits.

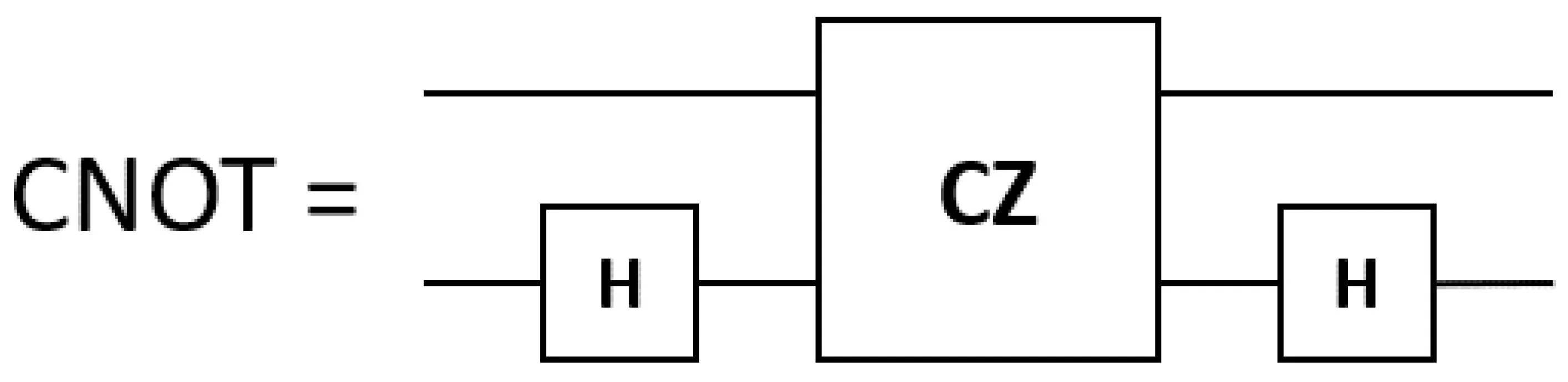
Fig.9. CNOT gate generated from CZ gate.

Table 2. Fidelities of two-qubit gates.

2.3. Qubit readout

For any quantum processor,readout is expected to be fast and of high fidelity. The readout method is dependent on the measured observables. For a charge qubit,the quantum information is stored in the electric charge on the superconducting island,which could be detected by a single-electron transistor(SET).[8]For a flux qubit, the persistent current of two states is different so that dc-SQUID can be used to detect them.[74]As for a phase qubit,it is much more likely to tunnel at higher levels. After sending a probe signal which induces the excited qubit to the next states with large tunneling probability, one can distinguish the two states according to the voltage across the junction.[10,23]

When the eigenstates of the observable are also stationary states,repeated measurement would produce the same results,which provides a way to increase the fidelity of measurement. Such repeatable measurements are called quantum nondemolition(QND)measurement.[75]A QND method in superconducting quantum circuits is the dispersive readout, which is also based on the qubit–resonator coupling model.[75]While frequency of the qubit and the resonator detunes significantly,i.e.,?=ωq?ωr?g,the system is in the dispersion regime.With dispersion coupling, the Hamiltonian of the system can be effectively written as

3. Superconducting quantum computing

3.1. Quantum computing without error correction

With the development of superconducting quantum computing device, some simple versions of quantum algorithms have already been implemented in real systems, providing practical demonstrations that a quantum computer can be fulfilled and have become fundamental step for further investigation.

Deutsch algorithm is the first proposed quantum algorithm.[79]Deutsch–Jozsa (D-J) algorithm is its improved version showing the advantages of quantum algorithm from making use of superposition states.[80]In 2009,Deutsch–Jozsa algorithm was performed in a two-transmon-qubit superconducting quantum processor by DiCarloet al.,and Grover algorithm was also performed in real machine for the first time.[81]

Proposed in 1994 by Peter Shor,Shor algorithm is aimed to compute prime factors for composite numbers for much shorter time than all classical algorithms do.[82]And since 1994, it has been regarded as a deadly threat to RSA protocol,whose ability of maintaining secrecy is dependent on the difficulty of factorizing big composite numbers.

Here is a brief description for Shor algorithm.[82]The problem of factorizing a large numberNcan be converted to the problem of findingr,the order in the multiplicative group of a random integera,that is,ar=1(modN). Here,ais relatively prime to and smaller thanN. Ifris not an odd number ora=?1(modN),thenashould be replaced by another random integer andrshould be calculated correspondingly again.With Euclid algorithm,it is easy to find the greatest common divisors ofar/2±1 andN,gcd(ar/2±1,N),as the prime factors ofN.The orderrequals the period of the functionfa,N(x),

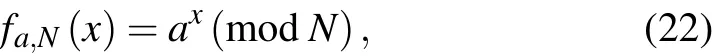
wherekis an integer. The fractionk/rcan be obtained in lowest terms by roundingy/2Lto the nearest fraction whose denominator is smaller thanN. This can be done with a continued fraction expansion ofy/2L. By repeating steps above forO(loglogr)times,the correctrcan be obtained with a high possibility.[82]Another version of Shor algorithm was proposed by Zalka.[83]Researchers have begun to try Shor algorithm for factorizing small numbers in experiments. In 2012,Martinis’group computed prime factors of 15 with a quantum processor consisting of 4 Josephson phase qubits.[84]

In 2009,Harrow–Hassidim–Lloyd algorithm(HHL)was proposed to solve linear systems of equations.[85]Usually the formalism of this problem isAx=b, wherexis unknown whileAandbare given. HHL has been changed into many different versions combining classical and quantum algorithm components. Recently, Chenet al.[86]presented a hybrid classical-quantum linear solver working in a NISQ quantum computer for handling situations with the matrixAuseful for Markov decision problems, such as reinforcement learning.Using classical computer to perform ancilla quantum encoding (AQE) of HHL, Leeet al.modified the original HHL algorithm and realized this hybrid HHL algorithm on IBM Quantum Experience (IBMQX).[87]The same results as that of original HHL were obtained and the depth of the quantum circuit was reduced,showing that hybrid algorithms are possible to be more resource-saving than pure quantum algorithms are.

Quantum approximate optimization algorithm (QAOA)was proposed by Farhiet al.in 2014.[88]QAOA is aimed to solve combinatorial optimization problems which belong to NP-hard problems difficult to solve with classical computers when inputs are large. Unlike sampling problems,[2]combinatorial optimization problems are more practical. Therefore,QAOA has potential to realize quantum supremacy and at the same time to solve some practical problems in the production and service. However,performing simulations of QAOA,Guerreschiet al.pointed out that quantum speedup would not be realized until the quantum computer with several hundreds of qubits is available.[89]Up to now,quantum supremacy demonstrated with QAOA has yet been implemented.

3.2. Error correction

In a classical computer,errors mean undesirable bit flips.However,errors in a quantum computer are beyond this situation, includingXerror andZerror, caused by erroneous gate operations or qubit decoherence.Xerror changes the probability of measurement results,|0〉or|1〉(bit-flip error),and Z error changes the relative phase between|0〉and|1〉(phaseflip error). Leakage, another important kind of error, means qubits leave the computational subspace.

An error rate is defined as the probability that an error appears on a qubit after a gate operation. And a gate fidelity,ranging from 0 to 1, represents the difference between the qubit state prepared by a gate and the ideal qubit state that one wants. To characterize errors produced during computation, researchers developed several experimental methods of measuring gate fidelities.

3.2.1. Error characterization

Error characterization methods, which are still being developed,include quantum process tomography(QPT)[90]and randomized benchmarking(RB).[91]

QPT was proposed the earliest.For ad-dimension Hilbert space of a series of qubits,QPT requiresd2input states andd4measurements, which produces a lot of data that need much time to analyze. Recently, Houel al.provided a new selfguided algorithm for QPT,achieving 1/nscaling when the unknown process is used forntimes,which has the same effect as that of traditional QPT.[92]

The research on RB is now focusing on realization of multi-qubit RB. Mcdayet al.[93]used three fixed-frequency transmons to perform RB and measured the three-qubit error per Clifford (EPC). By introducing certain coherent errors to the gates, three-qubit error was increased but could not be predicted precisely by simultaneous one-and two-qubit RB.Helsenet al.[94]brought a theoretical analysis that much fewer sampled sequences can reach the requirement of RB than that of standard RB.The required number of sampled sequences scales with the average error rate, but is not mainly dependent on the number of qubits.

If errors in different qubits are statistically independent and the error rate is lower than a threshold, it is possible to run a quantum program for arbitrary long time with errorcorrecting codes,even though the error-correcting gates bring errors. This has been proved by the threshold theorem.[95]

3.2.2. Early error-correcting codes

Error-correcting codes based on classical linear codes developed by Shor, Calderbank, and Steane were classified as Calderbank–Shor–Steane codes (CSS),[96–98]which were found to be a subset of a class of more general codes called stabilizer codes.[98,99]With the development of quantum computing devices,researchers found it difficult to utilize these codes in real machines because of restrict requirement of both accuracy thresholds and good connectivity between qubits. Therefore,surface codes and bosonic codes were proposed as more suitable and alternative schemes.

3.2.3. Surface codes

Surface codes were derived by Kitaev from toric codes.[100]Wanget al.came up with a better decoding algorithm for Kitaev surface codes, which can improve the threshold error rate to over 1%.[101]The algorithm requires that qubits are arranged in a 2D square lattice and are divided in two classes. One is called data qubit and the other is called syndrome qubit. Syndrome qubits identify errors of data qubits so that the measurement results affected by these errors can be corrected. In 2012, Fowleret al.provided a more practical version of surface codes which could be implemented with Xmon qubits[102]and described a way of constructing logical qubits with physical qubits. The structure of the surface codes is shown in Fig. 10. Here syndrome qubits are called measurement qubits,consisting of measure-Zqubits and measure-Xqubits. Measurement qubits detectZerrors andXerrors of data qubits around them. The implementation methods of single-qubit gates including Hadamard, S, and T and two-qubit gate like CNOT for logical qubits were also introduced in the literature,[102]which showed the possibility of building a universal quantum computer with surface codes.

Ghoshet al.studied the leakage in a two-qubit superconducting stabilizer measurement circuit and supplied two solutions: (a) using stabilizer-based topological error-correcting codes for qudits; (b) repeatedly initializing, operating, and measuring each qubit as additional steps of the standard topological error correction.[103]

Recently, Natalieet al.[104]investigated the influences of data leakage and ancilla (syndrome) leakage separately,showing two ways of maintaining the effectiveness of surface codes:confining leakage to data qubits and eliminating ancilla qubit leakage at the critical fault location.

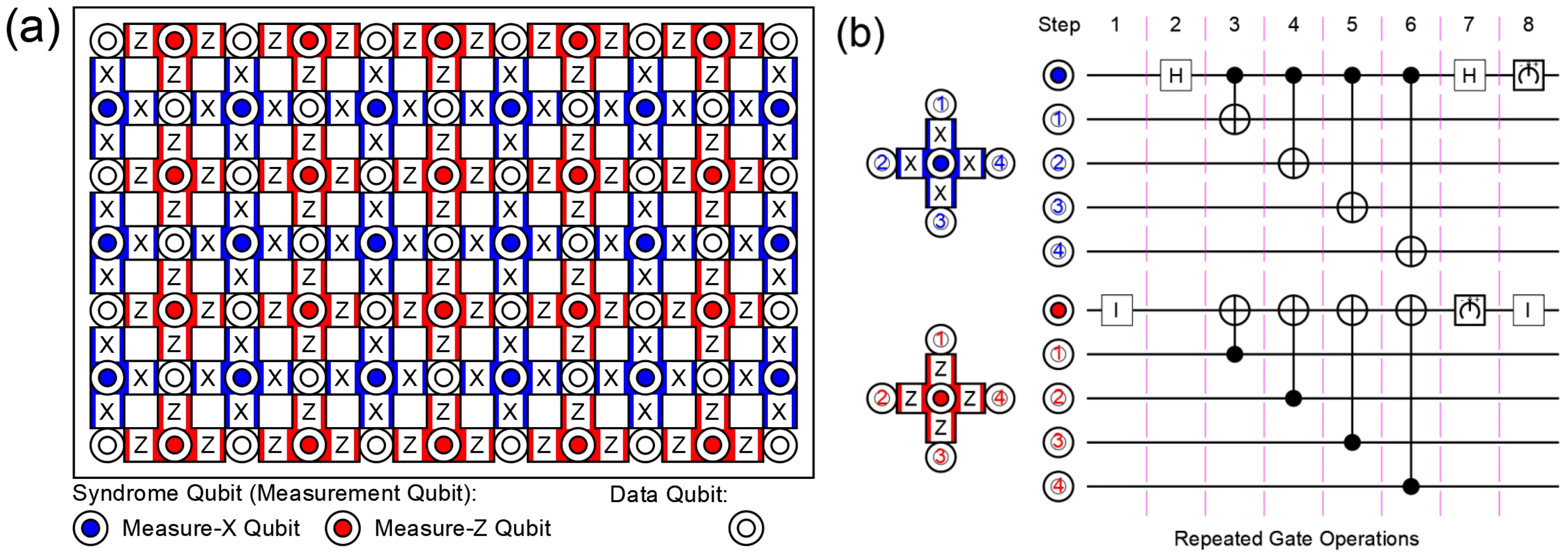
Fig.10. Schematic of circuits for realizing surface codes. (a)A 2D array implementation of surface codes. (b)Geometric sequences of operations(left),and quantum circuit(right)for one surface code cycle for a measure-X qubit and a measure-Z qubit.

The physical implementation of surface codes began in 2014.[105]Kellyet al.performed an experiment of protecting classical states from environment-induced bit-flip errors,with 9 Xmon qubits(4 measurement qubits and 5 data qubits)manufactured and arranged in a line alternately,forming a 1D surface codes architecture which was called repetition code.[105]The crisscross-like capacitors of Xmon qubits, coupling with neighbor capacitors for two-qubit gate operations, enable the architecture of surface codes to expand to a larger scale.

In 2017,Takitaet al.[106]demonstrated fault-tolerant state preparation in a superconducting circuit with five transmon qubits which constitutes the smallest surface code architecture,as shown in Fig.11.

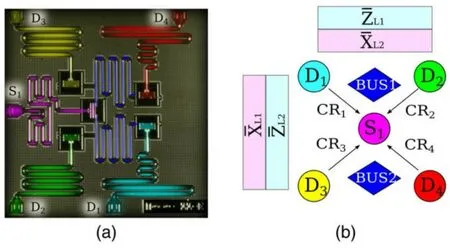
Fig.11. (a)False-colored micrograph of five transmon qubits. (b)Cartoon representation of a five-qubit lattice and the logical operators on the data qubits.[106]

Recently,using a superconducting circuit of surface codes consisting of seven transmon qubits (4 data qubits, 2Z-type ancilla qubits,and 1X-type ancilla qubit),Andersenet al.prepared logical states|0〉L,|1〉L,|+〉L, and|?〉Lof the encoded logical qubit.[107]

The main idea of surface codes is enlarging the number of physical qubits, so that logical qubits can be encoded in a Hilbert space with a large number of dimensions. However,with the increasing number of physical qubits,the noise channels increase proportionally. And non-localized multi-body interactions between physical qubits will make the control system and manipulation very complicated.

3.2.4. Bosonic quantum codes

Instead of obtaining a huge Hilbert space for encoding by adding many physical qubits,bosonic quantum codes,proposed in 1997,[108,109]make use of the infinite-dimensional Hilbert space spanned by energy eigenstates of a single quantum harmonic oscillator(bosonic modes)for encoding,reducing the requirement for hardware.

Mirrahimiet al.[110]proposed a paradigm of error correction by encoding quantum information in a quantum harmonic oscillator made of a cavity. These schemes required two- or four-component Schr¨odinger cat states as the logical qubit, which is called the cat codes. Wanget al.[111]realized a two-mode cat state of electromagnetic fields in two superconducting cavities,which had a strong dispersive interaction with an artificial atom made from Josephson junction. Rosenblumet al.[112]performed a CNOT gate between multiphoton qubits encoded in two cavities by coupling them to an RFdriven ancilla transmon,which is helpful for meeting the challenge of fast interaction between the two cavities without large nonlinearities and decoherence from the ancillary element.

Huet al.demonstrated the experiment of another kind of bosonic quantum codes,called binomial bosonic code.[113]The logical qubit was operated with universal quantum gate set with 97%average process fidelity and had a lifetime 2.8 times longer than that of uncorrected case. Recently, Maet al.[114]extended the error-transparent(ET)gates to the bosonic binomial code,which could tolerate errors occurred on the logical gates. The gate Hamiltonians of ET gates were designed by photon-number-resolved AC Stark shifts.

4. Superconducting quantum simulation

Quantum simulation was first proposed by Feynmanet al.in the 1980s,[115]to solve some quantum problems that would require exponentially increasing resources on classical computers with scale, which makes them intractable classically.Intuitively, quantum problems need quantum technology to deal with.[116]After decades of hard work, quantum simulation has made great progress and is expected to be applied in practical applications in the near future.[1,117]

4.1. Digital and analog quantum simulation

Quantum simulation takes a controllable quantum device to simulate other complex quantum system that is difficult to directly study and control.[3,118]The basic schematic is depicted in Fig. 12. The initial state|Ψ(0)〉of the quantum system and the time evolution operator, ?U,are mapped to the quantum simulator|ψ(0)〉and ?U′. After the evolution,the result of the simulator|ψ(t)〉is mapped back to the quantum system to obtain the required information. With quantum device,computational resources would not scale exponentially. Because of the relatively simple preparation,high degree of freedom in manipulation, high readout efficiency, tunable qubit frequency, coupling strength, superconducting quantum circuits have great advantages in quantum simulation. Moreover,since the particles in superconducting qubits are the excited states of the circuits but not physical particles,they need not obey the conservation law of particle number, which allows the simulation of non-equilibrium phenomena.[119–121]Generally, there are two types of quantum simulations, digital quantum simulation(DQS)and analog quantum simulation(AQS).[3,122]

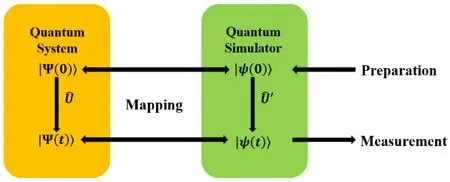
Fig.12. Quantum simulation.

4.1.1. Digital quantum simulation

Digital quantum simulation decomposes the complex dynamic evolution operator ?Uof the simulated system into a series of single-qubit or two-qubit gates that can be realized by quantum device.[117]Such a scheme is compatible with universal quantum computers with error correction. It does not mean that DQS is completely “universal”. In fact, there are some systems that DQS cannot effectively simulate.[3]In principle,DQS can effectively simulate any system whose Hamiltonian is finite-dimensional and local,but ineffectively for other problems. Fortunately, most of the interesting quantum systems have finite-dimensional local Hamiltonian. Therefore, DQS can effectively solve these problems.Generally,DQS includes three steps: initial state preparation,unitary evolution,and final state measurement.

Initial state preparationIt is crucial to prepare a good initial state for DQS, which affects the accuracy of the evolution result and the efficiency of the simulation. However,most initial states of practical systems are quite complicated or even unknown,so the preparation of initial states is a tough problem.[123,124]Fortunately,there are some efficient preparation methods for specific problems. For example,for the case that the initial state is a specified pure state,direct preparation is a valid method.[125]

Unitary evolutionThe decomposition of unitary evolution operator is the core step of DQS.[3,126]Considering only the local interaction, the Hamiltonian of the system can be written as

where ?Hlacts on at most a constantcnumber of systems.Since ?Hland ?Hl′ do not commute in most cases, it is difficult to decompose the time evolution into simple forms such as ?U=∏lexp(?i ?Hlt/?). The Lie–Trotter–Suzuki decomposition is commonly employed to deal with these unitary operators, which breaks the evolution time into many small time steps with a duration of ?t,

In this way, the simulator evolves gradually to approximate the actual dynamic behavior of the quantum system. Using the first-order Trotter formula,[127,128]it can be written as

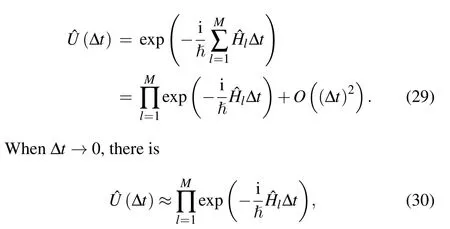
which is close to the actual evolution result of the original quantum system. To acquire more precision, higher-order Trotter formulas could be implemented, though it is much more complicated.

MeasurementThe last step of DQS is measurement, in which the desired information is obtained from the evolution result. Due to the characteristics of quantum measurement,all the information of the final state could not be extracted in one measurement. In principle,it is possible to obtain all the information in the final state with QST,but it will consume a lot of resources and thus seriously affect the efficiency of quantum simulation. For a given problem, extracting some quantities,such as correlation functions, operator spectrum, and so on,of a given state,and discarding some unwanted redundant information are much more practical,which improves measurement efficiency while obtaining effective information.[130]

4.1.2. Analog quantum simulation

Unlike digital quantum simulation,analog quantum simulation(AQS)does not decompose the evolution operator into many small steps, it directly maps the Hamiltonian of the quantum system to the simulator, taking advantage of their physical similarity.One can get some intuition of AQS with its classical counterpart: the analog classical simulation (ACS),which has been studied a lot in 20th century before rapid development of classical computers. A good example for ACS is to simulate a simple pendulum with an LC circuit. By observing the influence of circuit parameters on the input and output characteristics of the system, the relationship between the pendulum parameters and its dynamic behavior can be understood. Physical similarity of the two systems is utilized in this example. Since analog simulation requires a certain similarity of physical characteristics between the quantum system and the simulator, it is not universal. What physical system can be effectively simulated depends on the characteristics of the problem and the structure of the simulator.

A great advantage of AQS is that it is more efficient on the specific problems, and has less requirements on the physical characteristics of the simulator, such as the decoherence time of qubits. This feature allows AQS to operate effectively without error correction. Although it might be unable to achieve high accuracy, it is sufficient to obtain some results with less precision or certain qualitative conclusions. Therefore, AQS will be an important subject in the NISQ era,and it is expected that quantum simulation will demonstrate the advantages of quantum computers in practical applications before the implementation of universal quantum computers.[1,131]

The construction of the evolution operator corresponding to the simulated system on quantum simulator is simple for some systems, but sometimes it may also be rather complicated, requiring the participation of many auxiliary qubits or other structures. There is no universal method for this subject so far. In AQS, the initial state preparation is relatively simple, which in most cases can be prepared by relaxation.Due to the similarity between the target system and the quantum simulator, the readout of the final state is not complicated as well. It is generally sufficient to readout directly.In such procedures it is more efficient than DQS. One could also note that it is not always necessary to simulate the entire quantum system. To simulate part of dynamic behavior of the system is also sufficient in some cases. The rest can be done on a classical computer. It can also be combined with DQS to form digital-analog quantum simulation, making full use of the advantages of both methods,such as flexibility and efficiency.[132]The benchmarking of an analog quantum simulator remains an open question. A heuristic idea is to take some tasks that could be tackled with classical computers to be the benchmark.

4.2. Applications

Quantum simulators can solve some problems that are difficult to solve in classical calculations and experiments,having important applications in physics, chemistry, and biology. It has brought results that were previously difficult to obtain in many fields and will allow testing of some theoretical models. In addition,quantum simulation itself is a good platform for further study into quantum phenomena. In following sections we will introduce some applications of quantum simulation in some problems where superconducting qubits have shown their unique role, including Hubbard model, topological properties,open quantum system,quantum chemistry calculation,etc.

4.2.1. Hubbard model

Hubbard model is a highly general model in condensed matter physics, which describes the on-site interacting particles on a lattice. The Hubbard Hamiltonian takes the form[133]

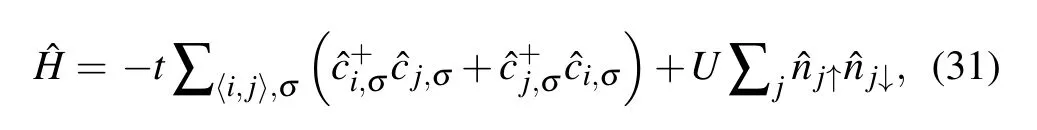
wheretparametrizes the “kinetic-energy”, andUis the onsite repulsion potential energy. The first term describes the near-neighbor hopping of a tight-binding model and the second term denotes the potential energy cost if two particles occupy a site. It seems simple, but for models more than one dimension with large number of particles,it is too difficult to treat classically.

Quantum simulation plays an important role in solving such problems. Las Heraset al.[134]proposed an implementation of the Fermi–Hubbard models with DQS, which consists of Jordan–Wigner mapping, Trotter decomposition, and multi-qubit gates. This paved the way for simulating complex fermionic dynamics with superconducting circuits,which was experimentally validated by Barendset al.latter.[135]Dallaire-Demerset al.proposed a hybrid quantum-classical approach to Fermi–Hubbard model and found out that the Trotter–Suzuki errors can be made as small as possible.[136]They also pointed out that thermodynamic properties of a complex fermionic lattice which are inaccessible for classical computers could be simulated in a quantum computer with a few tens of qubits.[137]Reineret al.showed how to simulate the one-dimensional Fermi–Hubbard model with a double chains of transmon qubits and proposed protocols for gaining confidence in the results of simulation.[138]According to Cai’s estimation,[139]it would be possible to implement a 50-qubit Hubbard model variational quantum eigensolver(VQE)in the NISQ era.

Except for Fermi–Hubbard model, Bose–Hubbard models have also been studied with superconducting quantum simulator. Roushanet al.implemented a technique for resolving the energy levels of interacting photons and benchmarked it by capturing the main feature of the intricate energy spectrum with a nine-qubit chain.[140]Maet al.built a Bose–Hubbard lattice for photons in strongly interacting regime to explore strongly correlated quantum matter, showing the power of superconducting quantum simulator in this field.[141]The above results are for 1D Bose–Hubbard models,which can also be solved by analytical methods.[142]Yanayet al.have proposed a scheme for implementation of the twodimension hard-core Bose–Hubbard model with an array of floating transmon qubits.[143]Yeet al.constructed a Bose–Hubbard ladder of 20 qubits on a 24-qubit superconducting processor, showing the way to simulate exotic logic particles by subtly encoding physical qubits.[144]Motivated by the quantum simulation on a ladder circuit, Liet al.found out that in the hard-core limit,the rung-pair localization can exist both at the edges and in the bulk,and the system can display a localization similar to the many-body localization.[145]

4.2.2. Topological properties

In condensed-matter physics, topology is an important fundamental concept. In recent years, searching topological states with superconducting qubits becomes a field of growing interest. It provides a powerful platform to research topological phenomena in physics which is difficult to study directly. In 2014, Roushanet al.investigated the topological properties of several quantum systems with a superconducting quantum circuit.[146]They have shown the power of the method in interacting quantum systems,discovering the emergence of a topological phase induced by interaction. From a superconducting qubit,Schroeret al.also observed a topological transition.[147]By mapping the momentum space of condensed matter to the controllable parameter space of superconducting quantum circuits,Tanet al.imaged a tunable gapless band structure which is typical of topological semimetals,and manipulated two topological quantum phase transitions.[148]In the latter works,they have observed the Maxwell points in the Maxwell metal bands,and Weyl points in Weyl-semimetal bands. Both the band structures can be manipulated.[149,150]In a one-dimension qubit chain,Caiet al.have measured the topological winding numbers and caught the phenomenon of topological magnon insulator states.[151]In 2020,the topological property of two-dimensional superconducting circuit was investigated.[152]

4.2.3. Open quantum system

In quantum computation, decoherence of qubits is what everyone tries to mitigate.However,it can also be exploited to study open quantum systems due to their similarity. In classical computation, it is much more difficult to simulate the dynamics of open quantum systems than closed quantum systems since the Lindblad equation requires more resources to solve than Schr¨odinger equation. Lloyd suggested that one can utilize the natural decoherence of quantum simulator to simulate open quantum systems.[116]In superconducting quantum simulator, open systems can also be described by the spin boson model.[153,155]In most cases,the spin–boson model that consists of a single two-level system coupled to bosonic modes could be directly mapped to superconducting qubits and resonators. It is possible for classical simulation to solve the problem in the limit of weak coupling, but impossible for strong coupling, which requires quantum simulation. Such model has provided a platform to reveal the complex quantum dynamics in the ultra-strong coupling (USC) regime.[156–158]Experiments have shown that the quantum Rabi Hamiltonian in USC regime could be simulated in superconducting quantum simulator,allowing the implementation of nonlinear process in which the number of excitations does not conserve. It also provided new avenues for nonlinear optics, concerning metamaterial,[159,160]phase transition,[161,162]and so on.

4.2.4. Quantum chemistry

Quantum computation and quantum simulation are also prompted by chemistry,since large scale exact first-principles calculations of molecular properties are intractable in classical computers.[124,163,164]Owing to the computational complexity, classical methods for chemistry simulation utilize many approximation techniques, trying to avoid explicitly describing the full many-body wave function and their propagation in time in a computation. However, such features could be implemented well in a quantum computer.

For static problems in quantum chemistry, a method based on the time-independent variational principle, VQE, is useful.[165,166]With VQE,it is possible to simulate the ground states of quantum systems. O’Malleyet al.are the first to report an electronic structure performed on a quantum computer with VQE and the canonical quantum algorithm for chemistry,computing the surface energy of H2. They found that the VQE is robust to certain errors.[167]Collesset al.applied quantum subspace expansion approach to the H2on a superconducting quantum chip, extracting both ground and excited states.[168]Kandalaet al.computed the ground-state energy for BeH2,whose size is much larger, on an experiment with up to six qubits.[169]This was the largest size in quantum simulations of chemistry before the simulation of isomerization mechanism of diazene implemented by Google AI Quantum ad Collaborators,using one dozen qubits.[170]One could see that quantum chemistry developed rapidly in recent years and it is expected to further demonstrate its ability in the NISQ era.

4.2.5. Other applications

Since quantum mechanics plays a fundamental role in modern physics, there are many other applications in quantum simulation. For example, Pedernaleset al.[171]showed that the dynamics of the Dirac equation and Klein paradox can be simulated on a superconducting qubit system, connecting relativistic quantum physics and circuit QED. Meiet al.[172]proposed a superconducting quantum simulator for the Holstein molecular-crystal model, opening avenues to study the electron–photon physics. Guoet al.observed a dynamical quantum phase transition in a simulation of the quantum-quench dynamics of many-body systems.[173]Xuet al.investigated the dynamical phase transition in the Lipkin–Meshkov–Glick model, showing that superconducting quantum simulation is useful for nonequilibrium quantum many-body systems.[121]Guoet al.proposed an energy-resolved many-body localization transition using a 19-superconducting-qubit processor, opening a route for the experimental research of many-body mobility edges.[174]

4.3. Quantum annealing

Quantum annealing (QA), developed from classical simulated annealing (CA), is designed to solve classical combinatorial optimization problems,[1,175,176]which have important applications in classification problems,[177]machine learning,[178]quantum chemistry,[179]and high-energy physics.[180,181]

The goal of optimization problems is to find the global minimum value of the cost function. However,there are usually a large number of local minima in the landscape of the cost function, which interfere the search of solutions. Thus, the combinatorial optimization problems are usually too complicated to solve directly. To deal with such problems, classical annealing uses a heuristic method to search for the global minima. As we know,the arrangement of the solid material is not always in the lowest energy state,but trapped in a metastable state. Annealing is applied to relax the material to its most stable state, i.e., the ground state. With thermal disturbance,it can temporarily deviate from the local minima and then surpass the potential barrier to search the entire energy landscape for the minimum value. Another important step is to reduce the thermal disturbance slowly, and finally stabilize the state at the global minimum. Quantum annealing solves the problem in a similar way.

In quantum annealing,quantum fluctuation plays the role of thermal fluctuation in classical annealing. Systems are disturbed by quantum fluctuation and tunnel across the potential barrier,but not surpass it,which lead the system to converge to the global ground state more efficiently than classical annealing in some problems.

Assuming that the Hamiltonian of the system to be dealt with is ?H0and the Hamiltonian associated with the external field is ?H1,the total time-dependent Hamiltonian can be written as[182]

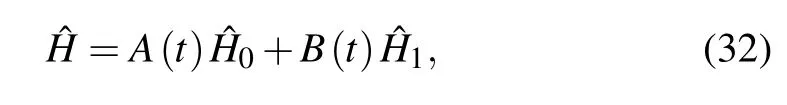
whereB(t) would gradually decrease fromB(0)=1 at first toB(τ) = 0, withτto be the computation time, whileA(t)would gradually increase fromA(0)=0 initially toA(τ)=1 at last. In this process, the system is initialized in the ground state of ?H1,which is easy to prepare experimentally,and then slowly transits to the ground state of ?H0,obtaining the required solution.

Without loss of generality, the transverse-field Ising model is a good example for quantum annealing, which has been experimentally realized with superconducting flux qubits.[183]The Hamiltonian of the device is

In 2011,D-wave released the first commercially available quantum annealing device,[183]and since then,a lot of proofof-principle experiments have been realized.With 1800in situprogrammable superconducting niobium flux qubits, Kinget al.demonstrated a large quantum simulation of a Kosterlitz–Thouless phase transition.[184]Harriset al.observed phase transitions between the paramagnetic, antiferromagnetic, and spin-glass phases with a 3D 8×8×8 model of interacting Ising spins.[185]Jianget al.proposed a framework for integer factorization problem by converting them to an executable Ising model.[186]

However, there is always a scientific debate on whether annealing devices can actually offer a speedup over classical computers.[176]R?nnowet al.proposed a method on how to define and measure quantum speedup. In their experiment,they did not find evidence for the speedup.[182]Albash and Lidar demonstrated the first example showing that the experimental quantum annealer has scaling advantage over classical simulated annealing with 95% confidence. However, it does not mean that it achieves a quantum speedup either.[187]There is some other discussion on this question.[188,189]

5. Challenges and perspectives

Error correction has been the core issue of the current stage of quantum computer implementation. However, scaling qubits should also be considered simultaneously. Nowadays articles about error correction are still focusing on looking for and implementing suitable error-correcting codes based on well-made qubits, but few of them notice that the yield of qubits is also significant for scaling quantum computer.Whether the randomly-distributed invalidated qubits are able to weaken the efficiency of surface codes,and how to improve the reliability of qubits and surface codes remain unsolved.Vedralet al.showed that the total number of qubits required for factorizing a big numberNis 7n+1,wherenis the number of bits used to encodeN.[190]Therefore,in order to factor a big number with 2048 bits,at least 14337 logical qubits are required. Assuming that we need about 4000 physical qubits to build a logical qubit,the algorithm requires 57348000 physical qubits,which has the order of magnitude around 107–108.Therefore, there is still a long period of time away from the date of breaking RSA2048 protocol,and error correction must be an unavoidable task.

Another challenge is improving synchronization and accuracy of gate operations. With millions of qubits in the same superconducting circuits,the quantum computer should be able to perform millions of accurate gate operations at the same moment,which requires high-speed,high-accuracy,and low-latency classical control modules.

There are still many unresolved problems in quantum simulation. In digital quantum simulation, it is a challenge to efficiently prepare the initial state. In terms of decomposing evolution operators,one needs to find a more efficient method that could minimize the required quantum gates while improving accuracy. For analog quantum simulation, how to benchmark the efficiency of the simulator is still an open question.Quantum annealing has shown its ability to surpass classical simulated annealing in some cases, but the question that whether it can in fact achieve quantum speed-up needs more detailed studies.

In summary, this review recalls the fundamentals of superconducting qubits and describes the progresses of quantum computing and quantum simulation, showing that many problems are still waiting for solutions. Error correction is required for universal quantum computers.Surface codes are the hopeful candidates for building large-scale quantum computers but need to be improved by tackling obstacles like leakage of qubits and qubit yield. Bosonic quantum codes could be developed further. As for quantum simulation, more practical applications of simulations are expected. Digital quantum simulation is compatible with the universal quantum computation,while analog quantum simulation is a much more unique framework which depends on the feature of physical realization. The experiments in the last two decades have been showing that superconducting qubits with circuit-QED architecture are promising physical systems for the realization of quantum computation and quantum simulation.