High-resolution angle-resolved photoemission study of large magnetoresistance topological semimetal CaAl4?
Xu-Chuan Wu(吳徐傳),Shen Xu(徐升),Jian-Feng Zhang(張建豐),Huan Ma(馬歡),Kai Liu(劉凱),Tian-Long Xia(夏天龍),and Shan-Cai Wang(王善才)
Department of Physics,Beijing Key Laboratory of Optoelectronic Functional Materials and Micro-nano Devices,Renmin University of China,Beijing 100872,China
Keywords:magnetoresistance,angle-resolved photoemission spectroscopy(ARPES),topological semimetal
1.Introduction
The discovery of the extremely large magnetoresistance(XMR)in semimetal WTe2[1]has attracted much attention to explore the origin of XMR.Magnetoresistance(MR)is the tendency for a material to change its electrical resistance in an externally applied magnetic field,which is widely used in spin devices,magnetic memory,and magnetic sensors.A series of materials with XMR have been found to exhibit very large unsaturated MR,meanwhile several effective mechanisms have been proposed to explain its origin.In electron–hole compensation mechanism,[2–8]the MR behavior changes quadratically with the magnetic field,written as MR=μeμhB2,whereμeandμhare the mobilities of the electrons and holes,respectively.In semimetals with comparable carrier density,such as PtBi2,[8,9]TmPn(Tm=Ta or Nb;Pn=N,P,As,Sb,Bi)[10–15]and YSb,[3]it can be explained by the carrier compensation mechanism well.The topological protection mechanism[16,17]can suppress the backscattering without magnetic field.The topological symmetry breaking can cause the XMR,in which the mobility of carries is highly dependent,such as Cd3As2,[18]TaAs family,[19]and ZrSiS family.[20–22]While other exotic mechanisms were proposed,open Fermi surfaces(FSs)have been observed in many XMR materials such as MoAs2,[23]SiP2,[24]andα-WP2.[25]A field-induced change in the FSs was also reported to play a significant role in the origin of XMR.[26]XMR has been observed among a wide scope of materials,however,the underlying mechanism of XMR is not completely understood.The near-quadratic field dependence of MR and a field-induced up-turn followed by a resistivity plateau at low temperatures become their obvious fingerprints.
Recently,CaAl4with large unsaturated MR up to 3000%at 2.5 K and 14 T accompanied with a plateau was reported,[27]and similar magnetotransport fingerprints characterized by a near-quadratic field dependence of MR and field-induced upturn in resistivity followed with a plateau at low temperature have also been observed.In this paper,by combining ARPES with the first-principles calculations and previous quantum oscillations,[27]we elaborate the topology of FSs and discuss the origin of the large MR in CaAl4.Although structural phase transition from I4/mmm to C2/m has been recognized,the subtle impact on electronic structure is observed by our ARPES measurements.The measured and calculated FSs show multiband characters and anisotropic carrier pockets.Electrons and holes cannot compensate well in the fitting of previous transport data based on isotropic two-band model,while the calculated carrier density still supports the compensation mechanism.Moreover,the Z2invariant of CaAl4equals 1 and the band yields nontrivial Berry phase.The contribution of the topological band structure to MR needs further experimental investigation.
2.Experimental details
High-quality single crystals of CaAl4were grown by the flux method.ARPES measurements were performed at the beam line 13U of the National Synchrotron Radiation Laboratory(NSRL)at Hefei with a Scienta D80 analyser and the Kr discharge lamp(hυ=10.05 eV)with a Scienta R4000 analyser at Renmin University of China.The energy and angular resolutions were set as 15 meV and 0.05°,respectively.The samples were cleaved in situ along the(001)plane and measured at T=25 K in a working vacuum better than 5×10?11Torr.The first-principles electronic structure calculations on CaAl4were carried out with the projector augmented wave(PAW)method.[28,29]The generalized gradient approximation(GGA)of the Perdew–Burke–Ernzerhof(PBE)formula[30]for the exchange–correlation function was adopted.The kinetic energy cutoff of the plane-wave basis was set to be 350 eV.A 20×20×20 k-point mesh was taken for the BZ sampling and the SOC effect was not considered.The lattice parameters and internal atomic positions were fully relaxed until the force on all atoms were smaller than 0.01 eV/?A.The FSs were calculated by performing the maximally localized Wannier functions(MLWF)method.[31,32]
3.Results
Figure 1(a)shows the schematic of CaAl4’s crystal structure determined by the single crystal x-ray diffraction(XRD)pattern.The single crystal and powder XRD patterns can be well refined with C2/m(No.12)space group.The refined patterns yield the lattice parameters:a=6.1695?A,b=6.1842?A,c=6.3451?A,andβ=118.05°,which was reported in our previous results.[27]Another study suggests a transition at 443 K from I4/mmm to C2/m is a continuous process.[33]In addition,a second transformation might occur at T≈243 K,which is revealed by the specific heat and the elastic modulus.[34]Our temperature-dependent XRD measurement from 5 K to 300 K has been performed to rule out the possible phase transition.[27]Tetragonal I4/mmm and monoclinic C2/m own a fourfold rotation axis C4and a twofold rotation axis C2,respectively.The electronic structures will be affected by the breaking of lattice symmetry,which will be further discussed in the ARPES measurement in detail.The cleavage plane oriented along the(001)direction is shown in Fig.1(b).The 3D Brillouin zone(BZ)with high symmetry points and the top view of BZ are illustrated in Figs.1(c)and 1(d),respectively.
Figure 2 demonstrates the high-resolution experimental contour intensity at T=25 K and the corresponding Fermi surface from first-principles calculations.As shown in Figs.2(a)and 2(b),the FS contour consists of a circular(α),four triangular(β)and a shuriken-like(γ)electron pockets centered at the Z points.Figure 2(b)plots the intensity maps at selected energies from EFto?1.0 eV,and there are more bands at high binding energies.The top of the hole-like band is located at?0.75 eV.Below?0.5 eV,βpockets disappear and there is a square pocket which connects interior of the pocketγ.To display the distribution of FSs in reciprocal space intuitively,two clusters of FSs are shown in Figs.2(c)and 2(d),respectively.The profile of the calculated FSs in Zplane is almost identical to the measured FSs through ARPES measurements.

Fig.1.Single crystal and Brillouin zone.(a)Crystal structure of CaAl4 with space group C2/m(No.12).(b)The cleavage plane(001)of the crystal.(c)Schematic of the 3D first BZ and the(001)-projected surface BZ.(d)Top view of the 3D BZ.
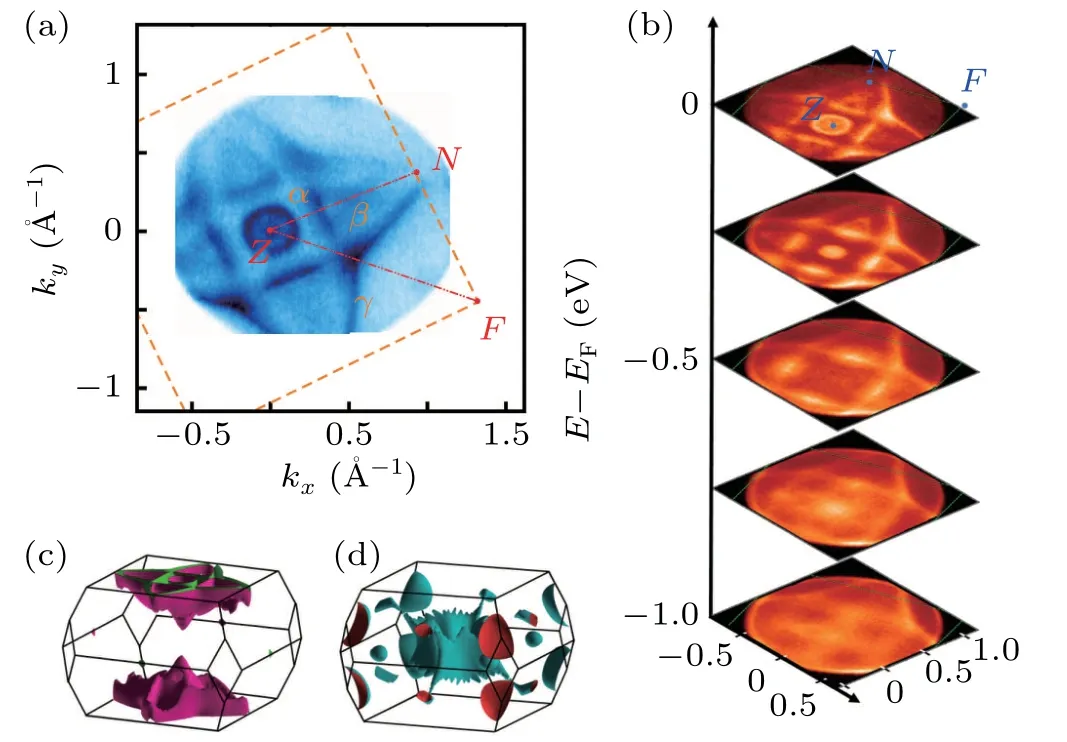
Fig.2.ARPES band mapping and calculated FSs in CaAl4.(a)Photoemission intensity map at the EF in kx–ky plane at T=25 K with hυ=21 eV,and the orange and red dashed lines indicate the 2D BZ boundary and the high-symmetry directions,respectively.(b)Photoemission intensity maps measured at energies from EF to?1.0 eV.(c),(d)The calculated hole-like and electron-like 3D FSs of CaAl4,respectively.
We have further verified the consistency between the experimental ARPES results(Figs.3(a)and 3(b))and the calculated band structures(Figs.3(c)and 3(d))along the high symmetry lines Z–N and Z–Y.The bandsα,β,γaround Z can be clearly identified.A careful comparison between the DFT calculations and the ARPES intensity plots along high symmetry directions also reveals the high reliability of the calculations.Therefore it is reasonable to predict electronic transport properties by fitting the effective mass of the bands and calculating the volume of the FSs based on the first-principles calculations.It is noteworthy that a mini-band structure indicated by the red arrow(Fig.4(f))near the EFcannot match any band in the bulk band calculations,and it can be also distinguished around Z in Fig.4(e),which is possibly attributed to the contribution from the surface states.
Figure 4(a)illustrates the results of the FS mapping in the k‖–kzplane along theΓ–M(Z–N)direction.The intensity modulation of the band structures along kzcan be clearly observed.The angle-dependent SdH oscillation measurement indicates an ellipsoidal FS and a quasi-2D FS.[27]Bandαis a circular pocket from the perspective of kx–kyplane.It is a narrow ellipse in k‖–kzplane and confirms that the FS of band αis an ellipsoid.The white dashed lines shown in Fig.4(a)indicate the independent characteristic of kz,which can also be verified in the calculated FS in Fig.2(d).The spectral intensity of crossing band happens to exchange with the increase of photon energy as shown in Figs.4(b)–4(d).It is consistent with the positions of two clusters of FSs(Figs.2(c)and 2(d))along the kzdirection.
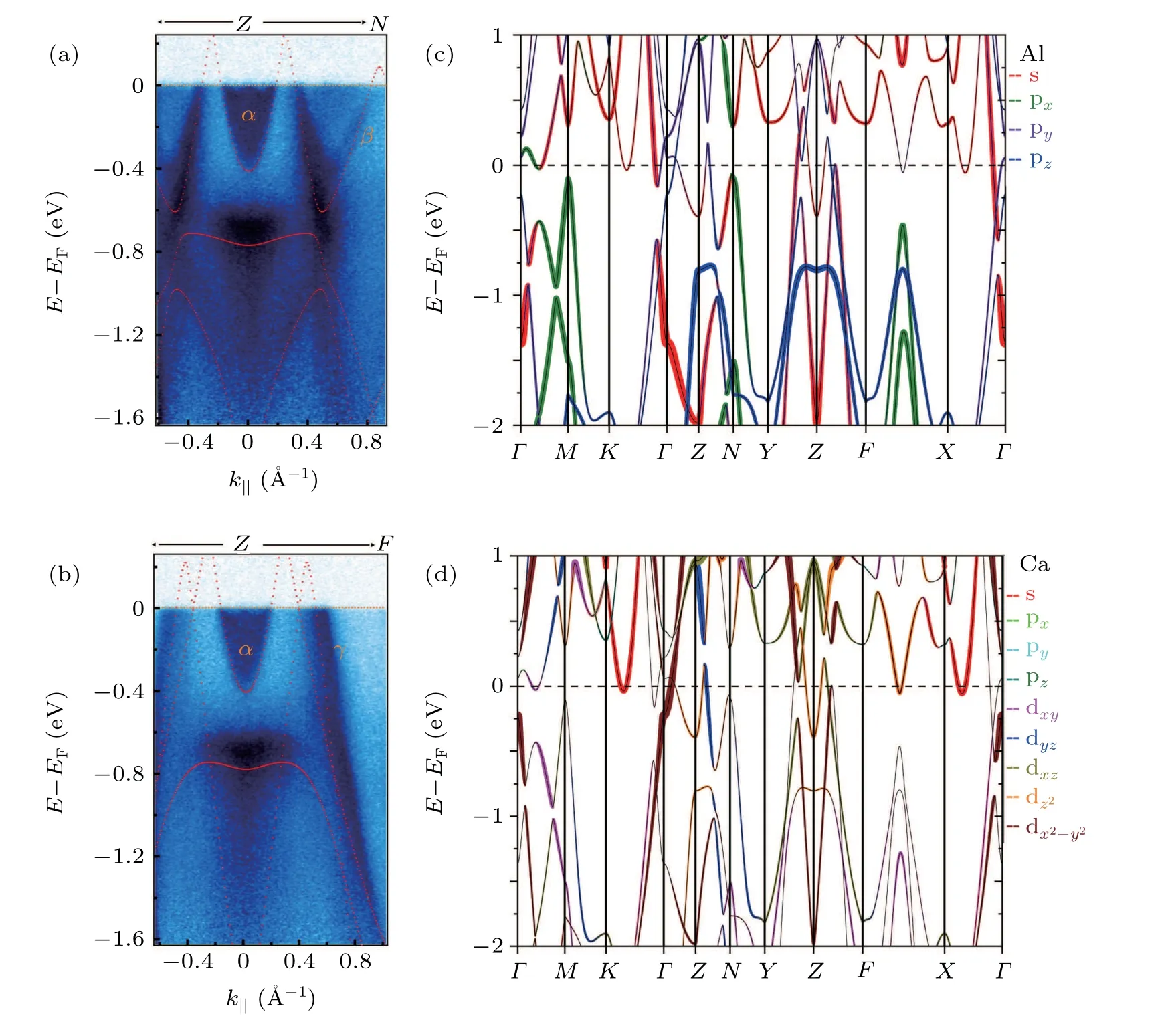
Fig.3.(a),(b)The photoemission intensity plots along the high symmetry lines N–Z–N and F–Z–F,respectively.The red overlaid dashed lines in ARPES data indicate the DFT calculations.(c),(d)The calculated orbital-projected bulk band structures along the high symmetry lines without SOC.
4.Discussion
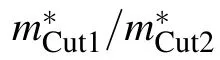

Fig.4.(a)Photon energy dependent experimental FS mapping of CaAl4.(b)–(d)The photoemission intensity plots along M(N)–Z(Γ)–M(N)with photon energy hυ=16 eV,27 eV,33 eV,respectively.(e)Photoemission intensity map at the EF in kx–ky plane at T=25 K with hυ=21 eV.(f),(g)The photoemission intensity plots along two groups of high symmetry lines withπ/2 angle,and corresponding directions are indicated by the orange and green dashed lines in(e).
It has been reported that CaAl4exhibited large unsaturated magnetoresistance~3000% at 2.5 K and 14 T.[27]The observation of XMR in semimetals has triggered intensive research on the origin of XMR.An isotropic two-band model with perfect electron–hole compensation can lead to a quadratic dependence of magnetoresistance on magnetic field.To identify the specific values of the carriers in CaAl4,a simplified two-band model has been developed to describe the Hall effectρyx(B)for the full temperature range

where ne,handμe,hare the concentration and mobility of electrons and holes,respectively.[27]Fitting of the transport data at T=2.5 K based on an over-simplified model yields that ne=3.5×1021cm?3,nh=4.5×1020cm?3,the mobilityμe=0.12 m2/V·s,andμh=0.2 m2/V·s.The ratio of ne/nhat T=2.5 K is approximately 7.8.which can explain the deviation B1.6field dependence.Luttinger’s theorem states that the volume enclosed by the FSs is directly proportional to the particle density.[35,36]Due to the high consistency between the first-principles calculation and ARPES measurements,we can integrate the volume of the electron and hole pockets in reciprocal space,0.1349?A?3and 0.1278?A?3for electron and hole pockets,respectively.The ratio of ne/nhfrom the calculation is approximately compensated.Therefore,we need to discuss whether the carrier concentration obtained by the MR fitting based on two-band model is reasonable.Such an imbalanced charge carrier densities fitting from the isotropic two-band model results in a saturating MR curve at intermediate magnetic field,unless a large distinction between the electron and hole mobility is considered for the fitting process.[3]However,it is contradictory that unsaturated MR up to 3000%at 2.5 K was observed in CaAl4.[27]The nonlinear Hall resistivity,angle-dependent SdH quantum oscillation experiments,and the DFT calculations indicate multiband feature and strong anisotropy of FSs.[27]Different orbitals from Ca and Al atoms go through the EFto form the complex FSs,shown in Figs.3(c)–3(d).As discussed before,an isotropic two-band model typically assumes uniform mobility in all directions for each type of carriers.Apparently,this assumption on the mobility is not rational,where the anisotropic FS has been shown in ARPES measurements and calculated FSs.It is necessary to consider the anisotropic multiband nature of CaAl4in a quantitative MR analysis.
To further explore the origin of large MR,possible topological protection in CaAl4is discussed by combing the ARPES with Z2invariant and Landau fan diagram of Landau level(LL)index yielding Berry phase(φB)in our previous work.[27]The extreme cross section of FS,angular dependence of the SdH peak,[27]and the calculated 3D FS in Fig.2(c)jointly confirm the existence of bandαshown in Fig.2(a).The LL index of bandαis approaching to a nontrivial Berry phase of 0.93π.[27]Moreover,there are both time-reversal and space-inversion symmetries in CaAl4with C2/m.The topological invariant Z2of CaAl4equals 1,which is calculated from the product of the parities of all the occupied bands at the eight time-reversal invariant momentum(TRIM)points.[27]We have not found the expected topologically nontrivial surface state and band crossing.Thus it is worth studying further to learn more about the topological protection mechanism.
5.Conclusion
In summary,we perform APRES measurements and carry out first-principles calculations to comprehensively describe the electronic structure of CaAl4.A subtle impact from the structural phase transition from I4/mmm to C2/m is observed.A quasi-2D FS can be confirmed by the kz-dependent ARPES and the calculated FSs.The origin of large MR in CaAl4is mostly attributed to the electron–hole compensation mechanism and topologically nontrivial electronic structures.Multiband features and the anisotropic FSs revealed by the ARPES measurements,the first-principles calculations and magnetotransport properties reveal the discrepancy of the carrier density ratio ne/nhbetween the isotropic two-band model and Luttinger’s theorem.Thus,a general multiple-band model and further ARPES measurements should be considered to explore the perfect compensation and electronic band topology.
Acknowledgment
The authors thank the technical assistance from the BL13U beamline in National Synchrotron Radiation Laboratory(NSRL).
- Chinese Physics B的其它文章
- Multiple solutions and hysteresis in the flows driven by surface with antisymmetric velocity profile?
- Magnetization relaxation of uniaxial anisotropic ferromagnetic particles with linear reaction dynamics driven by DC/AC magnetic field?
- Influences of spin–orbit interaction on quantum speed limit and entanglement of spin qubits in coupled quantum dots
- Quantum multicast schemes of different quantum states via non-maximally entangled channels with multiparty involvement?
- Magnetic and electronic properties of two-dimensional metal-organic frameworks TM3(C2NH)12*
- Preparation of a two-state mixture of ultracold fermionic atoms with balanced population subject to the unstable magnetic field?

